重视方法指导,培养几何直观
吴建华
有关倍的知识的教学内容,旧教材分别安排在二年级上册和二年级下册,而修订后的教材集中在三年级上册中编排,好处有三:一是由于倍的知识后移,使得学生学习的难度降低;二是教学用倍的知识解决问题——求一个数是另一个数的几倍、求一个数的几倍是多少的问题,不再受到所学的乘除法知识的限制,教学内容的呈现更具逻辑性;三是集中教学用乘除法解决包含有“倍”数量关系的实际问题,有利于学生在解决问题中加深对乘除法含义的理解,了解所学的知识的用途和价值,从而逐步培养学生应用数学的意识和解决问题的能力。
纵观新旧教材,新教材在问题解决教学中更重视传统的“应用题”教学与新课标下的“问题解决”之间的关系,在教学过程中注重继承“应用题”教学的优良教学经验,实现了从 “应用题”到 “问题解决”的教学传承,重视方法指导,培养几何直观,从而提高学生解决问题的能力。现以“求一个数的几倍”为例,从三个方面来剖析本课。
一、看传统的“应用题”教学与新课标下“问题解决”教学的有效融合 ——“应用题”教学的创新
1. 抓住了“问题解决”的教学关键:两个转化
抓住了“问题解决”教学中“阅图”与“数量关系”这两个关键,引导学生从生活情景中获取有用的信息,抽象成数学问题,再运用不同的方法分析、理解数量关系,并用数学方法求解,实现了“从情景图到文字应用题”的转化和“从数量关系到算式”的转化。在第一个转化的过程中,教师要引导学生阅读与理解,引导学生充分经历用语言表述问题,然后把学生表述的图意用文字板书在黑板上,形成应用题的模式。学生的这一“说”与教师的这一“写”,搭建了从情景图到数学问题的桥梁,是图画情景向文字应用题转化的注脚点,使“应用题”与“问题解决”得到交汇结合。
2. 突出“问题解决”的教学核心:数量关系的分析与理解
遵循“感悟——认识——深化”的认知规律,我在导入环节设计“猜老师年龄”的游戏活动,意在让学生了解数量关系存在于事理当中,借助情景“事理”能帮助理解“数理”,感悟数量关系是“问题解决”的关键。
在新授知识环节中,要注重从三个方面引导学生认识和深化数量关系。
(1)注重多种分析方法的渗透与运用,数形结合,信息技术与学科整合;逐步从感性到理性,从直观到抽象理解数量关系、掌握分析数量关系的方法。
在《求一个数的几倍是多少》的问题解决教学中,我运用了多种方法进行教学。引入部分的猜年龄实际上运用了分析法,要求老师的年龄还需要知道什么条件;新授课部分运用了综合法,根据题目信息,能提出什么问题,然后借助几何直观,让学生进行思考分析,但这需要教师精心的指导。在教学中,我运用了操作法和画图法等方法,让学生通过摆小棒或画图方法帮助理解;画线段图是学生分析数量关系的重要手段,但对于三年级学生而言,线段图毕竟是抽象的,为了让学生更好地理解两个量之间的倍数关系,应引导学生抓住重点句,再通过“示意图——方框图——手势——小棒长——线段图”进行梳理,如图1。在这过程中,我充分利用信息技术并运用转化的方法,帮助学生将“求一个数的几倍是多少”的问题和乘法的意义联系起来,即“求几的几倍就是几个几相加”,然后再用乘法进行解决。
(2)注重算式各部分含义的理解,结合情景中的事理理解“题目实际求的是什么”,突出“把谁看作1份,谁有几个这样的1份”,强化理解“求一个数的几倍是多少”,数量关系中每个数量所表示的意义。
(3)注重题目的结构特征与数量关系特征的理解,认识“倍比”类问题是关于两个量之间的比较关系的问题,其中反映了两个量之间数量关系的那个句子就是重点句,重点句是解题的思路入口;数量关系特征突出对“1倍量”(标准量)的理解,求“一个数的几倍是多少”实际上是求若干个标准量是多少,这个标准量就是“每份数”,解题时要找准这个“每份数”。
二、看“问题解决”课堂教学的处理 —— 从具体到抽象的概括提升
我在课堂中及时利用了学生在学习过程中动态生成的资源,如图2。
由“具体实物——图形数量——数”逐步抽象,从感性的认识提升到理性的认识,发展了学生的思维水平。
引导学生通过借助图形直观把握数学对象,进行数学思考,即首先把研究“对象”抽象成为“图形”,再把“对象之间的关系”转化为“图形之间的关系”。这样就把研究的问题转化为“图形的数量或位置关系”的问题,借助几何直观进行思考分析。
三、看“问题解决”课堂练习的设计与实施 —— 数学模型的构建
新授知识环节的练习中,我预设了求“4个6?邛4个9?邛4个10?邛4个100是多少?”的学习活动,对问题进行概括提升:“这些问题都是求‘几的4倍是多少,都用乘法来计算。”由一个例题引申到一类问题。同时,学生能从这个练习设计的演变中,体会“总数量是随着1份量的改变而改变的”,深刻认识到解决这类问题的时候,找准1份是多少是关键。这个教学目标的预设抓住了问题的本质,目标的生成达到了举一反三、深化理解的效果,为构造“几的几倍就是几个几”用乘法算这个数学模型奠定了很好的基础。
巩固环节的练习中,我也预设了如图3的教学结构。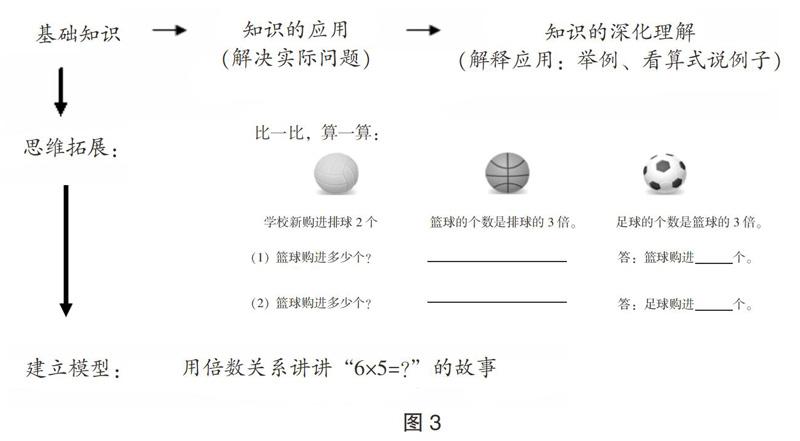
练习设计的构思是:横向从基础知识到知识的解释应用,纵向从基础知识到思维的拓展到该数学模型的建立。练习的实施采用了不同的思维训练方式,从“一倍数确定而倍数不定”和“一倍数不定但倍数确定”这两个方面多层次练习,最后还通过讲故事的方式来帮助学生建立“一个数的几倍是多少”的数学模型。这样的练习既夯实了基础又深化了认识,还拓展了思维,构建了该问题解决的数学模型,教学效果达到了预期目標。

