基于Plackett-Burman试验设计的超稠油SAGD影响因素研究

王建俊， 鞠斌山

(1中国地质大学能源学院·北京 2中国地质大学非常规天然气能源地质评价与开发工程北京市重点实验室·北京)

蒸汽辅助重力泄油理论(以下简称SAGD)是由加拿大的Butler教授于1981年首次提出[1]，大量学者对影响SAGD开发效果的因素进行了研究。Kisman等人[2]通过研究得到低注汽压力可以使Burnt湖地区SAGD油汽比高但产油量低；Ito等人[3]对隔夹层和注汽压力进行了敏感性分析；刘尚齐[4]基于传统的单因素分析方法对SAGD的影响因素进行了研究；Tavallali等人[5]分析布井方式对薄层油藏SAGD的影响，并对注采井间垂向距离与水平偏移距离进行优化；Tamer等人[6]的研究表明布井方式对蒸汽腔的发育特征及采收率均有显著的影响。Jiang[7]对矿场生产数据进行分析，得到不同地质条件下，井型、井组排距及注汽压力等对开发效果的影响不同。当利用传统方法对多个影响因素进行研究时，不能确定因素的影响程度大小，并且工作量大，无法顺利或者及时完成必要的工作。采用Plackett-Burman[8]试验设计方法可以综合研究多个因素并且确定影响权重，能极大地减少工作量。针对国内辽河油田馆陶组超稠油油藏SAGD的开发，选择9个主要影响因素，基于Plackett-Burman试验设计，利用数值模拟手段，研究不同因素对SAGD开发效果的影响。

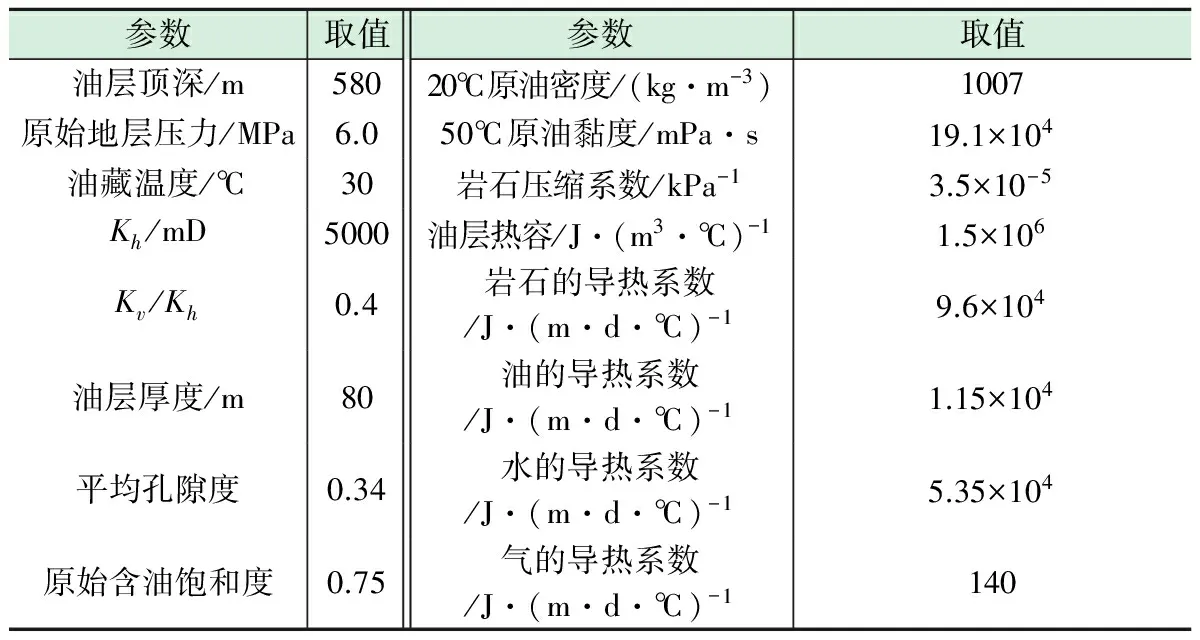
表1 油藏和流体性质参数表

一、SAGD模型建立

以辽河油田馆陶组油藏性质为基础(见表1)，利用CMG软件中的STARS模块建立三维模型。所建模型中共有3对双水平井SAGD井组，水平井的井轨迹与X方向平行。模型网格长度分别为：X方向25 m，Y方向4 m，Z方向2 m。

二、Plackett-Burman试验设计

考虑9个不同开发因素对SAGD开发效果的影响。首先确定因素范围取值，然后进行9因素两水平的Plackett-Burman试验设计。

1. 因素选择及其取值范围

结合SAGD现场生产及前人的大量研究，选择蒸汽干度、注汽速度、注汽压力等9个因素进行研究并确定取值范围。由于只有蒸汽的汽化潜热用于油层的加热，蒸汽干度要尽量高[9]。在最大吸汽能力和排液能力的范围内，注汽速度要尽可能提高，保证较高注汽干度。注汽压力较高时，注入温度较高，可以大幅度降低原油黏度和蒸汽腔中残余油饱和度，但是注汽压力影响蒸汽腔的压力，蒸汽腔压力过高将会抑制蒸汽腔的扩展且增加热损失[10]。采注比是指排液速度与注汽速度的比值，采注比过高会有蒸汽被直接采出，降低泵效；而过低时冷凝液聚集，影响蒸汽腔的发育。排距为不同SAGD井组之间的距离，Singhal等人[11]指出大多数情况下，蒸汽腔垂直水平井方向扩展长度不超过50 m，因此排距应在100 m以内。SAGD井组中的垂向距离决定生产井的位置，通常垂向距离的取值范围为5～15 m。汽阻控制可以防止蒸汽进入产出液，Ito等人认为SAGD汽阻控制合理值范围为15℃～30℃[12]，Edmunds等认为是20℃～30℃[13]，模型中汽阻控制选择5℃～20℃。生产井水平段过长，注入蒸汽的干度、温度和流压损失增加，远端加热效果差；而水平段过短，无法充分发挥水平井的优势，结合油藏特征确定水平段取值为300～500 m。因素取值范围见表2。

表2 九个因素及取值大小表

2. Plackett-Burman设计及数值模拟结果

针对9个因素，选择两个水平，进行Plackett-Burman试验设计，共运行24次，与传统单因素方法的至少512(29)次运行相比，大大减少了工作量。以采收率与油汽比作为SAGD开发效果的评价指标，运行结果详见表3。

表3 试验设计及数值模拟结果

三、敏感性分析

因素权重确定对Plackett-Burman设计的运行结果进行多因素方差分析，结果如图1和图2，得到9个因素对采收率的影响程度由大到小依次为：注汽压力>采注比>排距>水平段长度>注汽速度>启动阶段周期数>垂向距离>蒸汽干度>汽阻控制；对累计油汽比的影响程度由大到小依次为：蒸汽干度>注汽压力>水平段长度>注汽速度>启动阶段周期数>排距>汽阻控制>采注比>垂向距离。可见，影响采收率的三大因素依次为注汽压力、采注比与排距，其权重分别为38.8%、22.3%、11.4%，这三者权重之和达到70.5%；影响累计油汽比的三大因素依次为蒸汽干度、注汽压力、水平段长度，其权重分别为41.2%、40.5%、8.7%，这三者权重之和达到90.5%。

图1 影响采收率的因素权重排序图

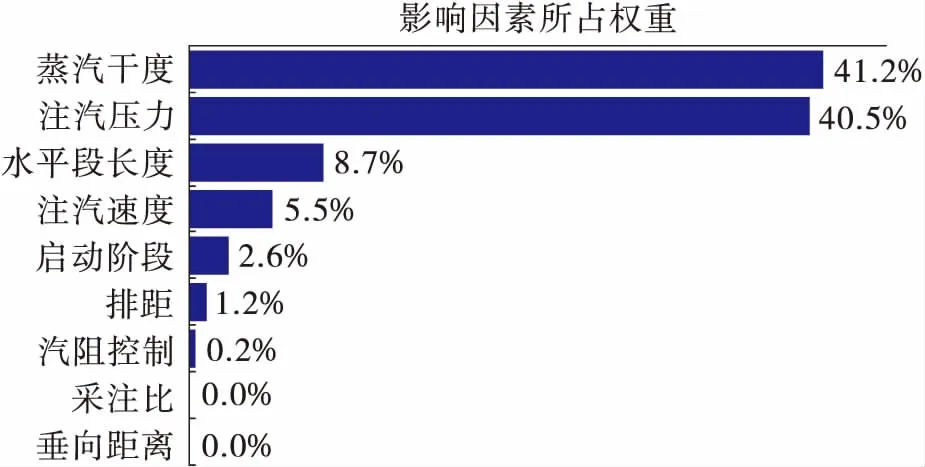
图2 影响累计油汽比的因素权重排序图

四、因素最优值研究

对模型结果的深入分析，回归出采收率(RF)与累计油汽比(COSR)计算公式，见式(1)和式(2)，利用公式计算结果与数值模拟结果进行对比，见图3与图4，可见回归公式精度较高。

RF=64.75+1.38A+0.00793B-1.448C+13.71D-0.0981E+0.262F-0.033G-1.446H-0.01836J

(1)

COSR=0.1807+0.288A-0.000157B-0.03429C+0.0129D+0.000742E-0.00057F-0.000832G+0.2165H+0.000398J

(2)

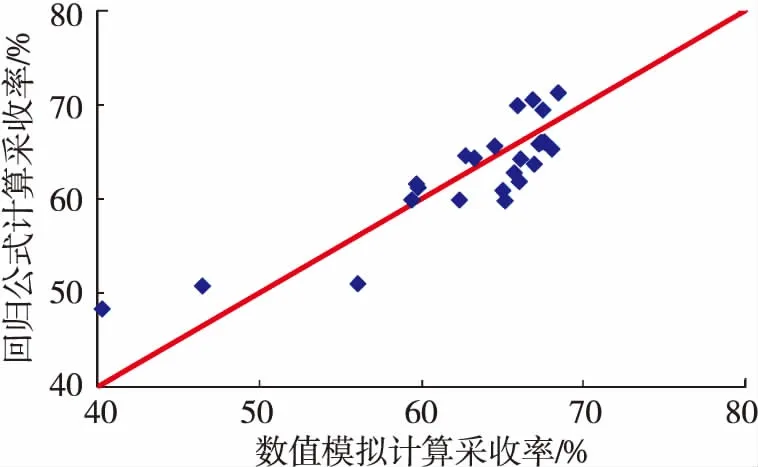
图3 数值模拟与回归公式计算采收率对比

综合两个评价参数，得到各因素最优值，即双目标最优化问题。利用满意度函数[14]解决这一问题：先将各个响应变量转换为单个满意度函数，再计算单个满意度函数的几何平均得到整体满意度函数。设响应变量y的目标为T，下限为L，上限为U，则单个满意度函数定义见式(3)，式(3)中，r1、r2分别为权重值。单个满意度函数的几何平均见公式(4)。

图4 数值模拟与回归公式计算油汽比对比

(3)

d=(d1d2…dm)1/m

(4)

根据式(3)与式(4)，当r1、r2分别取值0.5、1.0、2.5，得到采收率与累计油汽比的满意度函数，分别见图5与图6，权重值不同，曲线凹凸性变化明显。

取r1=r2=1，采收率目标值定为65%，累计油汽比目标值定为0.4 m3/m3，得到不同因素的最优取值见表4。根据得到的因素取值，运用数值模拟手段进行验证，采收率和累计油汽比的结果64.7%，0.382 m3/m3，且误差较小，满足工程精度。

图5 采收率的满意度函数

图6 累计油汽比的满意度函数

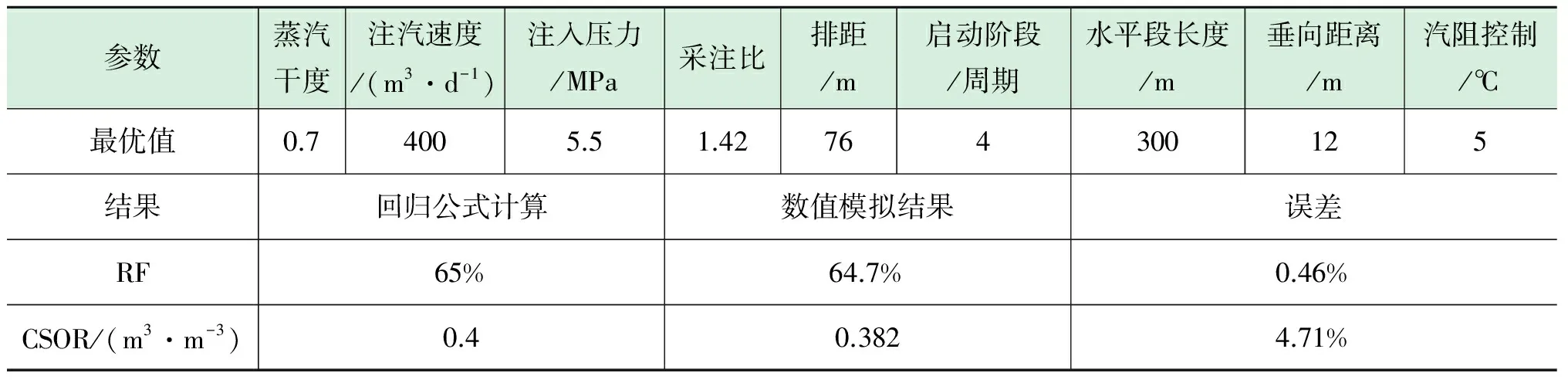
参数蒸汽干度注汽速度/(m3·d-1)注入压力/MPa采注比排距/m启动阶段/周期水平段长度/m垂向距离/m汽阻控制/℃最优值0．74005．51．42764300125结果回归公式计算数值模拟结果误差RF65%64．7%0．46%CSOR/(m3·m-3)0．40．3824．71%

五、结论

(1)选择影响SAGD开发效果的9大因素并且合理取值，基于Plackett-Burman试验设计建立了24个运行方案，不仅工作量大大减少，而且能综合确定各因素的影响权重。

(2)以采收率和累计油汽比作为评价指标，得到9个因素对采收率的影响程度由大到小依次为：注汽压力>采注比>排距>水平段长度>注汽速度>启动阶段周期数>垂向距离>蒸汽干度>汽阻控制；对累计油汽比的影响程度由大到小依次为：蒸汽干度>注汽压力>水平段长度>注汽速度>启动阶段周期数>排距>汽阻控制>采注比>垂向距离。并且得到了每个因素与评价指标之间的正负相关性，回归出了评价指标的计算公式。

(3)利用满意度函数进行双目标最优化，确定因素的最优取值。其中，采收率目标值定为65%并且累计油汽比目标值定为0.4 m3/m3时，各参数的最优取值分别为：注汽干度0.7、注汽速度400 m3/d，注汽压力3.5 MPa，采注比1.42，排距76 m，启动阶段吞吐周期数为4个，垂向距离12 m，汽阻控制为5℃。利用数值模拟手段进行验证，采收率和累计油汽比的结果64.7%，0.382 m3/m3，且误差较小，满足工程精度。

[1]Butler R M, Mcnab G S, Lo H Y. Theoretical studies on the gravity drainage of heavy oil during in-situ steam heating[J].The Canadian Journal of Chemical Engineering, 1981,59(4):455-460.

[2]Kisman K E, Yeung K C. Numerical study of the SAGD process in the Burnt Lake oil sands lease[A].SPE 30276,1995.

[3]Ito Y, Hirata T, Ichikawa M. The effect of operating pressure on the growth of the steam chamber detected at the Hangingstone SAGD Project[J]. Journal of Canadian Petroleum Technology, 2004,43(1):47-53.

[4]刘尚奇,王晓春,高永荣,等.超稠油油藏直井与水平井组合SAGD技术研究[J].石油勘探与开发, 2007, 34(2): 234-238.

[5]Tavallali M, Maini B, Harding T. Assessment of SAGD well configuration optimization in Lloydminster heavy oil reserve[A].SPE 153128,2012.

[6]Tamer M, Gates I D. Impact of different SAGD well configurations(Dover SAGD phase B case study) [A]. SPE 155502,2012.

[7]Jiang Q, Thornton B, Russel-Houston J. Review of thermal recovery technologies for the Clearwater and Lower Grands Rapids formations in Cold Lake, Alberta[J]. Journal of Canadian Petroleum Technology, 2010,49(9):57-65.

[8]Milliken W J, Levy M, Strebelle S, et al. The effect of geologic parameters and uncertainties on subsurface flow: Deepwater depositional systems[A]. SPE 109950,2007.

[9]Gates I D, Chakrabarty N. Optimization of steam assisted gravity drainage in McMurray Reservoir. Journal of Canadian Petroleum Technology[J].2006,45(9):55-62.

[10]Pooladi-Darvish M, Mattar L. SAGD operations in the presence of overlaying gas cap and water layer-effect of shale layers[J]. Journal of Canadian Petroleum Technology,2002,41 (6):40-51.

[11]Singhal A K, Ito Y, Kasraie M. Screening and design criteria for steam assisted gravity drainage (SAGD) projects[A]. SPE 50410,1998.

[12]Ito Y, Suzuki S. Numerical simulation of the SAGD process in the Hangingstone oil sands reservoir[J]. Journal of Canadian Petroleum Technology,1999,38(9):27-35.

[13]Edmunds N R. Investigation of SAGD Steam Trap Control in Two and Three Dimensions[J]. Journal of Canadian Petroleum Technology,2000,39(1):30-40.

[14]Derringer G C and Suich R, Simultaneous optimization of several response variables[J]. Journal of Quality Technology 1980, 12(4): 214-219.