基于键合图的空气制动机建模方法研究
吴萌岭,祝 露,田 春
(同济大学 铁道与城市轨道交通研究院,上海 201804)
传统的空气制动机是气动部件和机械部件相互耦合的复杂系统,目前仍然被广泛运用在货物列车和旅客列车上。这种制动系统在一百多年的改进发展中主要依靠设计人员的经验和大量试验,虽然也有科技工作者试图用经典控制理论对制动机关键部件进行理论分析,但终因空气制动机,特别是其核心部件分配阀的复杂而难以实现完整的理论分析。近几十年随着计算机技术的发展,研究人员运用各种数学建模手段探索空气制动机分析方法,把握系统内部的因果传递关系,以便找出结构优化的方向。
文献[1-3]基于气体流动理论建立了货车120分配阀和KZ1型控制阀的一维非等熵气体流动数学模型,文献[4-7]建立了列车管和分配阀模型。上述研究多局限于气体动态建模,忽略了多能域耦合对动力学模型的影响。此外通过中间变量将各能域子系统的动力学方程联立求解,这一过程繁琐、易出错、有误差,且不易得到适合现代控制理论的状态方程。
也有学者利用等效原理对空气制动机进行图形化建模。文献[8]利用AMESim建立制动系统中继阀模型,文献[9]利用AMESim建立货车120型制动机模型,文献[10]通过AMESim软件建立货车制动系统的分配阀和列车管模型。这些研究不需关注气路的数学模型,可简化建模过程。但是建立的模型不能与实际物理模型之间形成一一对应关系,降低了系统分析的可读性。
此外,文献[11]利用试验数据拟合函数进行建模,其模型中的司控室制动阀、分配阀均没有根据阀的实际机械结构精确建模,而是将其视为“黑箱”。基于统计的模型移植性和拓展性较差,无法满足系统分析的需求。
因此,找到简洁、统一的建模方法真实描述空气制动机的全局耦合和瞬时离散特性显得至关重要。基于键合图的方法能用统一的方式处理多能域耦合的系统,且与各部分物理结构以及各动态影响因素间具有直观而形象的一一对应关系,已在机械、故障检测和自动控制等领域得到了广泛应用[12-15]。为此,本文以120型空气制动机为例,提出键合图和MA(Model Approximation)法相结合的建模方法,建立具有统一因果关系的子系统数学模型,根据各子系统之间的功率流传递路径建立120型空气制动机的键合图模型,利用该模型分析空气制动机的工作特性。仿真试验结果表明:基于键合图的建模方法是研究空气制动机工作特性的一个有效手段,也为以后实现模拟测试奠定了基础。
1 120型空气制动机结构特点
空气制动机主要由列车管、分配阀(120阀)、副风缸、加速缓解风缸和制动缸等部件构成,图1为120型空气制动机结构示意图。

图1 120型空气制动机结构
120阀是空气制动机的核心部件,由主阀、半自动缓解阀、紧急阀、紧急二段阀、局减阀和加速缓解阀6部分组成。通过控制列车管中压缩空气的压强移动各阀体活塞位置,从而实现空气制动机在初充气、减速缓解充气、缓解充气、第一阶段局减、第二阶段局减、常用制动、紧急制动、紧急二阶段制动、制动保持和加速缓解等10种工作模式的切换。为了简化模型,做如下假设:
(1)不考虑半自动缓解阀对120型空气制动机制动特性的影响;
(2)气体流经阀体为等熵过程,与外界的热交换、摩擦生热可忽略不计;
(3)风源视为恒定压力源;
(4)气体气感对系统的影响忽略不计;
(5)管道连接处以及阀内外的泄漏忽略不计;
(6)机械系统中的滑动摩擦忽略不计。
2 子系统键合图的建立及数学模型
根据120型空气制动机的工作原理以及结构特点,可将该系统简化为9个子系统:列车管子系统、主阀子系统、紧急阀子系统、紧急二段阀子系统、局减阀子系统、加速缓解阀子系统、制动缸子系统、加速缓解风缸子系统以及副风缸子系统。根据各子系统的工作模式引入可控结点和虚拟元件,结合其工作原理绘制各子系统的键合图,再根据键合图建立各子系统的状态方程。下面以紧急阀子系统为例,建立该子系统的键合图模型以及状态方程。
2.1 120型空气制动机紧急阀键合图
紧急阀有三种工作模式,即充气缓解、常用制动以及紧急制动。在不同工作模式中,紧急活塞杆、先导阀以及放风阀的运动状态是不一样的,所对应的紧急活塞杆下部径向孔、先导阀径向孔和放风阀口的开关情况也不尽相同。
为了建模时能准确模拟模式切换这一离散特性,在键合图理论中引入可控节点。然而可控结点状态的变化,与可控结点相连的键合图元件的端口因果关系也将相应地发生变化。为避免这种情况的出现,利用MA方法,引入虚拟元件“MR-”,模拟对应通孔的开关状态,得到不同工作模式下的具有统一因果关系的键合图,如图2所示。
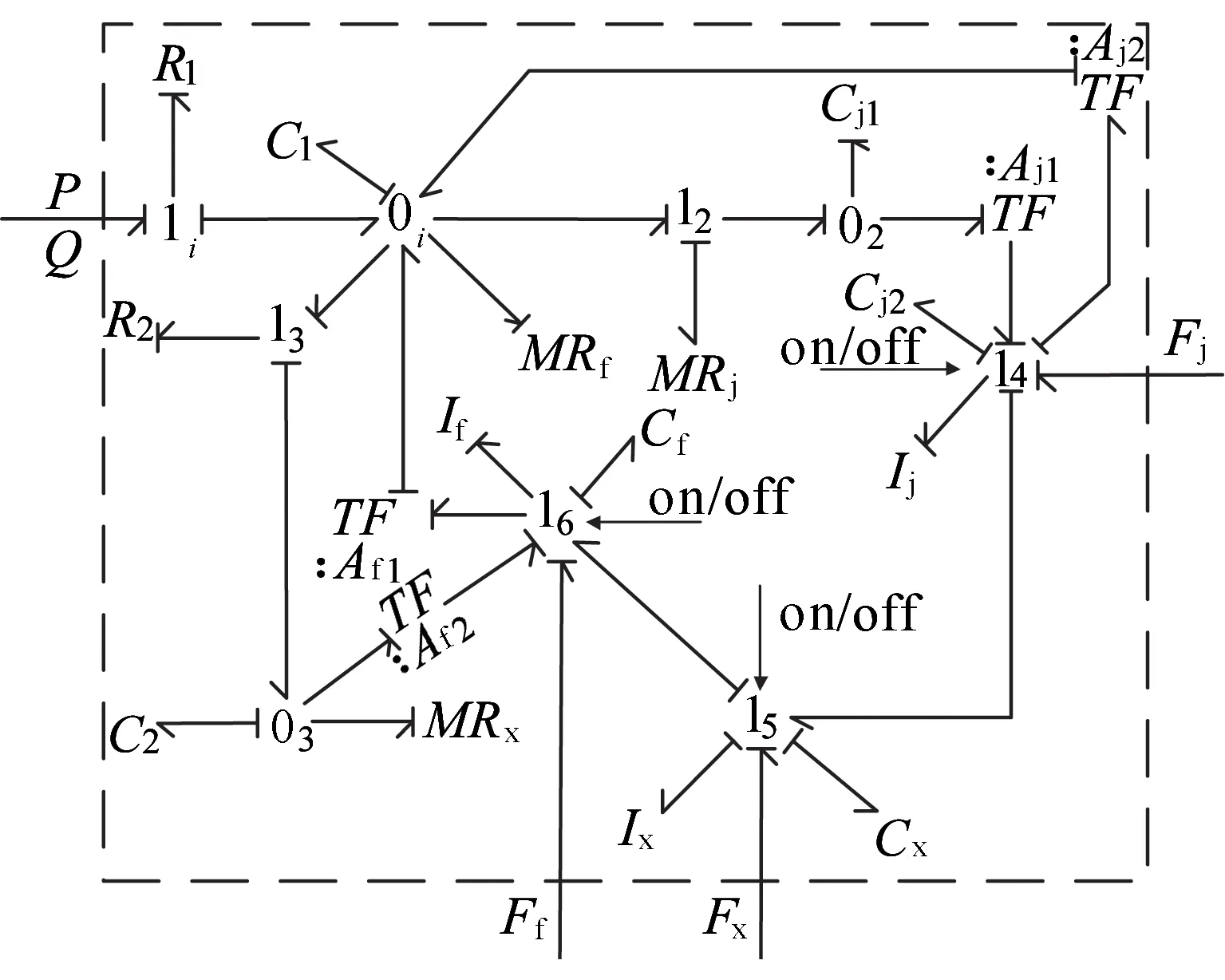
图2 紧急阀键合图模型
图2中可控结点14、15和16分别描述的是紧急活塞、先导阀以及放风阀的运动状态,“on/off”表示对应结点的连通与切断。P和Qjj分别为列车管指向紧急阀的空气压力和流量;Fj、Fx和Ff分别为安定弹簧、先导阀弹簧以及放风阀弹簧的预紧力;Aj1和Aj2为紧急活塞上下有效截面积,Af1和Af2为放风阀的上下有效横截面积;Ci(i=1,2,j1,j2,x,f)为容性元件,分别对应于安定弹簧室、放风阀弹簧室、紧急室、安定弹簧、先导阀弹簧和放风阀弹簧;Im(m=j,x,f)为惯量元件,分别对应于紧急活塞、先导阀以及放风阀;MRj、MRx和MRf为虚拟的阻性元件,分别表示紧急活塞杆下部径向孔、先导阀径向孔以及放风阀阀口;Rk(k=1,2)为阻性元件,分别对应于过滤器、Ⅵ缩孔。
2.2 120型空气制动机紧急阀状态方程
图2中,虚线框内描述子系统内部功率流,虚线框外为子系统同其他系统以及外部的能量交换的关系。由键合图理论可整理出紧急阀的状态方程为
xjj=Ajj+xjj+BjjUjj
其中
xjj=[q1q2qj1qj2qxqfpj2pxpf]T
Ujj=[PFjFxFf]T
式中:xjj为紧急阀子系统内部变量;Ujj为紧急阀子系统外部输入;pm、qm、cm和rm分别为m元件的动量、变位、容度参数和阻性系数;其中主要元件有安定弹簧室(m=1)、放风阀弹簧室(m=2)、紧急室(m=j1)、安定弹簧(m=j2)、先导阀(m=x)、放风阀(m=f);a,b,c为定义的布尔变量,表示可控结点的状态,即取值为1或0。
3 空气制动机键合图的建立及数学模型
3.1 120型空气制动机键合图
系统能量不仅在子系统内部进行传递,还在子系统与子系统之间进行能量交换,进而完成一系列复杂的动作。为了更好地展示各子系统之间的耦合关系,将各子系统视为“黑箱”,根据子系统之间的功率流向以及因果关系绘制如图3所示的120型空气制动机键合图,其中虚线框将120分配阀子系统细化为多个二级子系统。
在图3中,虚拟元件MRz、MRj、Rf、MRs分别表示主阀通往制动缸、局减阀、副风缸以及加速缓解风缸的通孔,该通孔的关闭状态是由主阀活塞的运动位移决定的。在120型空气制动机键合图模型中,可将副风缸、加速缓解风缸、制动缸视为容性元件。

图3 120型制动机键合图模型示意图
3.2 120型空气制动机状态方程
以紧急阀为例(详见图2),虚线框内为紧急阀的内部结构描述,而外部接口是与其他系统的能量交换。通过图2所示的功率流向以及因果关系可知,P为列车管子系统对紧急阀子系统的外部输入,Qjj为紧急阀的外部输出。由键合图理论进一步推导可得出紧急阀子系统对列车管子系统的外部输出为
yjj=Cjjxjj+DjjUjj
其中
yjj=[Qjj]T
因此,各子系统的状态方程可表示为
yi=Cixi+Dizi+Viui
式中:i(i=1,2,…,9)为空气制动机的子系统;xi为子系统的状态变量;yi为该子系统的外部输出;zi为其他子系统对该子系统的外部输入;ui为整个系统的外部输入。显然该子系统的zi可通过其他子系统的yj求得。因此,空气制动机的状态变量为
x=[x1x2x3x4x5x6x7x8x9]T
其状态方程为
⋮
4 仿真结果验证与分析
4.1 仿真验证
以初充气和紧急制动全过程为例,运用Matlab/Simulink软件对120型空气制动机键合图模型进行仿真求解。以恒定压强600 kPa向直径为25 mm的列车管初充气,待副风缸和加速缓解风缸的压力恒定后实施紧急制动,此时列车管以80 kPa/s的速度减压直至压力为0。图4、图5分别为初充气和紧急制动的仿真结果。

图4 初充气压力曲线
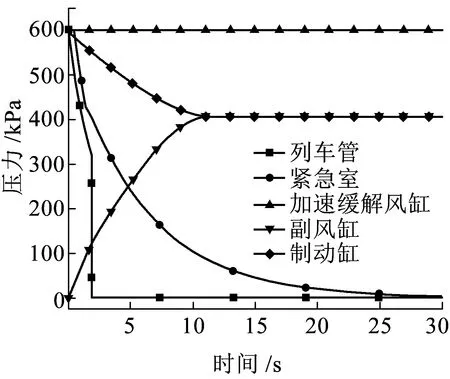
图5 紧急制动压力曲线
由120阀在705型试验台上的性能试验可知,初充气试验标准为:副风缸压力充到580 kPa的时间为180~230 s,副风缸压力达到580 kPa时加速缓解风缸压力大于550 kPa;紧急二段跃升试验标准为:配用356 mm制动缸时压力由0上升到400 kPa时间为9~11.5 s,制动缸跃升压力120~160 kPa。文献[9]在客货单车综合试验台上得到120阀紧急阀性能试验数据:紧急室初充气时压力从0充到580 kPa用时为48.1 s;从放风阀开启到紧急室压力降为40 kPa,用时13.2 s。
初充气时列车管快速升压至600 kPa,120阀主阀活塞在列车管压力的作用下向下运动,打开副风缸与列车管之间的通路。由图4可以看出,副风缸充压到580 kPa时的时间为190.1 s,此时加速缓解风缸压力为555.4 kPa,制动缸压力为0。紧急阀紧急活塞在列车管压力的作用下紧压紧急阀体,此时紧急室压力经过紧急活塞轴向缩孔Ⅲ和缩孔Ⅳ从0充压到580 kPa,耗时45.8 s,仿真误差为4.78%。
实施紧急制动时,紧急阀的紧急活塞杆向下运动顶开放风阀,加快列车管排气速率;而由于紧急活塞杆缩孔Ⅴ的作用,紧急室向列车管逆流速度减慢,因此出现了如图5所示的列车管和紧急室压力曲线的突变过程。当紧急室压力降至40 kPa时用时14.1 s,仿真误差为6.82%。在列车管紧急排气作用下,120阀主阀活塞向上运动,关闭副风缸孔和加速缓解风缸孔,打开副风缸向制动缸充气的通路。由图5可以看出,制动缸压力和副风缸压力变化分为两段,这是由紧急二段阀作用引起的。制动缸跃升压力为146.8 kPa,当压力升至400 kPa时用时10.2 s,最后平衡压力为406 kPa。加速缓解风缸压力维持在600 kPa。
通过比较分析模拟结果和试验数据发现,仿真结果和试验数据吻合较好,证明模型具有较高计算精度,能够较好地模拟系统在运行过程中的动态特性。
4.2 故障仿真
以模型为基础进行仿真研究的目的之一是充分发挥数学模型模拟能力强、数据完善、经济性好、周期短等特点进行各种故障仿真,得到仿真对象较为完备的故障特征,为故障模拟测试打下基础。本文分别以机后起“非常”现象为例,利用模型进行故障仿真。通过对120阀结构分析发现,引起120阀机后起“非常”现象的可能因素包括安定弹簧老化、紧急活塞杆轴向中心孔堵塞以及缩孔Ⅵ松动,故障工况的关键参数见表1。

表1 故障工况与正常工况的关键参数
4.2.1 正常工况分析
如图6(a)所示为120阀在正常状态下工作时列车管、紧急室的压力变化曲线。由图6(a)可知,初充气时紧急室升压至580 kPa时用时45.8 s;在常用制动后列车管和紧急室的压力分别保持在202.1、203.7 kPa,紧急室和列车管之间存在着0.16 kPa的压力差,这是由紧急活塞杆轴向中心孔的限流作用引起的。图6(b)为正常工况下紧急活塞的运动位移曲线(设紧急阀未充气时紧急活塞的初始位置为零点,向下为正方向)。在初始状态时紧急活塞在安定弹簧的预紧力下压紧紧急阀体,因此在初充气阶段紧急活塞位移为0;实施常用制动后,紧急活塞开始向下运动(最大行程为0.96 mm)并最终在安定弹簧的弹簧力下恢复到初始位置。
因为紧急活塞杆最大行程<4 mm,未能顶开放风阀,所以此时紧急阀没有产生列车管紧急排气,即紧急制动未触发。
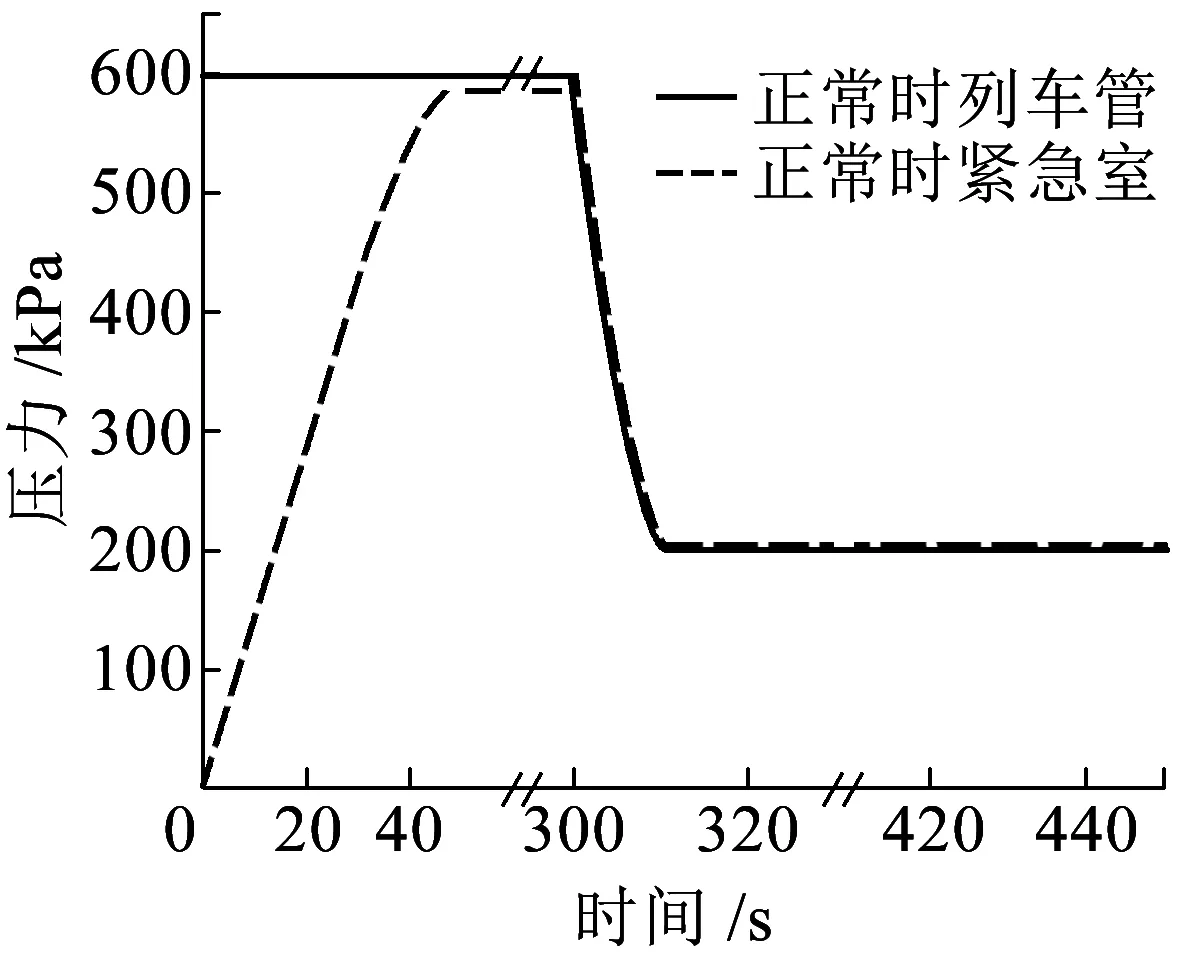
(a)列车管和紧急室压力曲线

(b)紧急活塞位移曲线图6 正常工况
4.2.2 故障工况分析
(1)安定弹簧老化
如图7所示为正常工况和安定弹簧老化工况的列车管、紧急室压力变化曲线以及紧急活塞位移曲线。由图7可知,安定弹簧老化时列车管和紧急阀排气速度均比正常工况快,最终列车管压力为0,而紧急室的压力维持在14.06 kPa。这是因为安定弹簧老化使得紧急活塞杆与先导阀之间难以保持正常间隙,从而引起意外紧急制动(紧急活塞最大行程为7.17 mm>4 mm)。此外,由于安定弹簧预紧力的消失,紧急活塞在自身重力、活塞两侧压力以及放风弹簧预紧力的共同作用下在位移4 mm处保持静止状态。在该处,紧急活塞杆可顶开先导阀的排风孔并打开紧急活塞杆上的径向缩孔Ⅴ,从而使得紧急室和列车管的压力差较正常工况大。

(a)列车管和紧急室压力对比

(b)紧急活塞位移对比图7 工况一:安定弹簧老化
(2)紧急活塞杆轴向中心孔堵塞
从图8可知,紧急活塞杆轴向中心孔堵塞使得紧急室的充排气速度略有降低,增大了紧急室和列车管的压力差,触发了意外紧急制动(紧急活塞的最大行程为17.90 mm)。其中,初充气时紧急室充压至580 kPa所需时间为48.5 s,充气速度降低6.35%;制动时,紧急室压力最终维持在16.36 kPa,制动管压力迅速降为0。

(a)列车管和紧急室压力对比

(b)紧急活塞位移对比图8 工况二:紧急活塞杆轴向中心孔堵塞
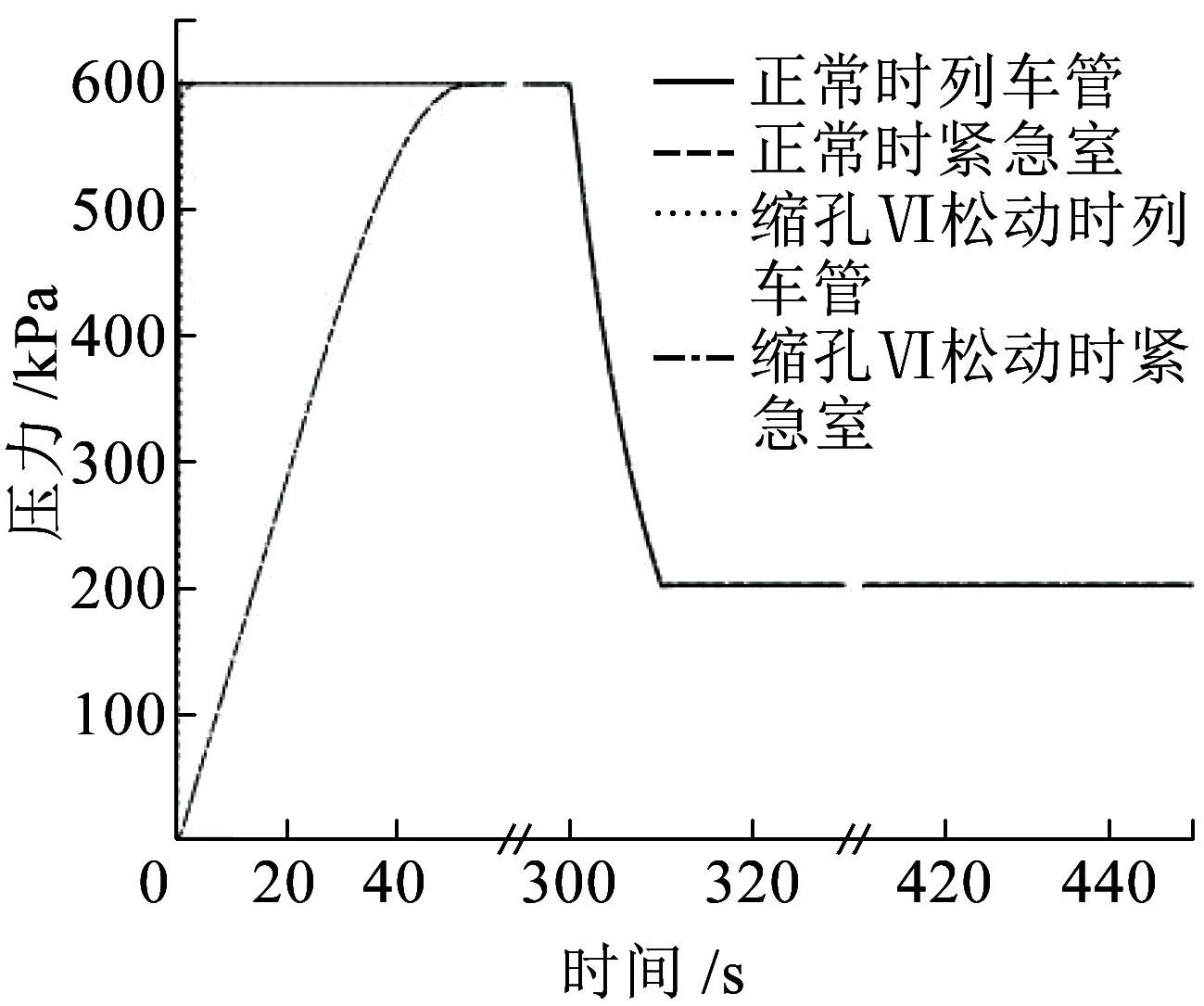
(a)列车管和紧急室压力对比

(b)紧急活塞位移对比图9 工况三:缩孔Ⅵ松动
(3)缩孔Ⅵ松动
从图9可知,初充气和常用制动全过程这两种工况列车管、紧急室的压力曲线以及紧急活塞位移基本一致。这是因为缩孔Ⅵ的松动只是影响了放风阀下部压力,当紧急活塞杆位移≤4 mm时对紧急活塞杆的运动无影响。
5 结论
本文以空气制动机的离散特性和多能域耦合为建模重点,在键合图的基础上引入虚拟元件,并以120型空气制动机为例进行仿真建模,利用该模型对120阀机后起“非常”现象进行研究。
(1)运用键合图建立120型空气制动机的数学模型,并得出其状态方程,与孤立研究各子系统相比,键合图模型能够真实描述系统动态特性及各子系统之间的耦合关系,易得到适合现代控制理论的状态方程。
(2)本文建模方法首先将大系统划分为各个子系统,然后再将子系统分解为基本元件,不但层次分明,方法简洁,而且所建系统的结构和耦合关系清晰,易于掌握。
(3)120型空气制动机键合图模型是由各子系统模型耦合而成的,能与真实物理系统形成一一对应关系。因此,模型可任意拆装和集成,也可对某子系统模型中参数或结构进行调整而不影响各子系统之间的关系,是120型空气制动机设计改进的有效方法。
参考文献:
[1]魏伟. 120阀及试验台的计算机模拟[J].铁道学报,2000,22(1):31-35.
WEI Wei. Computer Simulation of 120 Vehicle Distributing Valve and Tis Test Rig[J]. Journal of the China Railway Society,2000,22(1):31-35.
[2]赵阳,魏伟. 120阀内孔径对制动系统性能的影响[J]. 铁道科学与工程学报,2012,9(1):68-73.
ZHAO Yang, WEI Wei. The Effect of the 120 Valveaperture to the Brake System Performance [J]. Journal of Railway Science and Engineering, 2012,9(1):68-73.
[3]魏伟,刘涛,张军. KZ1型控制阀仿真模型及列车制动性能仿真研究[J].中国铁道科学,2010,31(1):105-110.
WEI Wei, LIU Tao, ZHANG Jun. The Simulation Model of KZ1 Control Valve and the Simulation Study on Train Braking Performance [J]. China Railway Science, 2010,31(1):105-110.
[4]MURTAZA M A,GARG S B L. Brake Modelling in Train Simulation Studies [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail & Rapid Transit,1989,203(2):87-95.
[5]MURTAZA M A,GARG S B L. Transients During a Railway Air Brake Release Demand [J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail & Rapid Transit,1990,204(1):31-38.
[6]PIECHOWIAK T. Pneumatic Train Brake Simulation Method [J]. Vehicle System Dynamics,2009,47(12):1473-1492.
[7]PIECHOWIAK T. Verification of Pneumatic Railway Brake Models [J]. Vehicle System Dynamics,2010,48(3):283-299.
[8]伍智敏,任利惠,裴玉春,等. 地铁列车制动系统的中继阀性能仿真[J]. 城市轨道交通研究,2011,14(9):52-57.
WU Zhimin, REN Lihui, PEI Yuchun, et al. Simulation of Relay-valve of Metro Braking System Performance [J]. Urban Mass Transit, 2011,14(9):52-57.
[9]杨璨,倪文波,蒋冬清,等. 基于AMESim的120紧急阀的建模及仿真分析 [J]. 铁道机车车辆,2009,29(6):37-39.
YANG Can, NI Wenbo, JIANG Dongqing, et al. Modeling and Simulation Analysis of 120 Emergency Valve Using AMESim [J]. Railway Locomotive, 2009,29(6):37-39.
[10]PUGI L,MALVEZZI M,ALLOTTA B,et al. A Parametric Library for the Simulation of a Union Internationale Des Chemins de Fer (UIC) Pneumatic Braking System[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail Rapid & Transit,2004,218(2):117-132.
[11]CANTONE L,CRESCENTINI E,VERZICCO R,et al. A Numerical Model for the Analysis of Unsteady Train Braking and Releasing Manoeuvres[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail & Rapid Transit,2009,223(3):305-317.
[12]SAEED B, AMIR K. Causality in Vector Bond Graphs and Its Application to Modeling of Multi-body Dynamic Systems [J]. Simulation Modeling Practice and Theory,2006,14(3):279-295.
[13]BORUTZKY W. Bond Graph Model-based Fault Detection Using Residual Sinks [J]. Journal of Systems and Control Engineering, 2009, 223(3): 337-352.
[14]牛刚,赵亚君. 基于键合图模型的机车制动系统故障检测与隔离[J].同济大学学报:自然科学版,2015,43(6):894-899.
NIU Gang, ZHAO Yajun. Bond Graph Model Fault Detection and Isolation for Locomotive Brake [J]. Journal of Tongji University :Natural Science, 2015,43(6):894-899.
[15]MARQUIS F W, MOUHIB O, CHEREJI B, et al. Bond Graph Formulation of an Optimal Control Problem for Linear Time Invariant Systems [J]. Journal of the Franklin Institute, 2008, 345(4): 349-373.

