HSE06方法研究CaB6电子结构、 成键特性以及理论光学性质

徐娟娟， 陈 晨， 杨洪军

(1. 内蒙古大学 满洲里学院， 内蒙古 满洲里 021400； 2. 吉林大学 仪器科学与电子科学工程学院， 吉林 长春 130061)

二价碱土六硼化物具有低密度、 高熔点、 高强度、 高杨氏模量、 高化学稳定性以及强耐离子轰击能力和强抗氧化能力等非金属难容化合物的特点， 在一定温区内热膨胀系数接近零[1]， 现已被广泛应用于热电材料， 核控制材料以及储氢材料等领域[2-3]. 最近， 人们在微量La掺杂的CaB6中发现了弱铁磁性， 而且其居里温度非常高(TC≈600 K)[4]. 此外， 在Ca缺陷的Ca1-δB6中同样发现了铁磁性[5]. 这引起了研究人员的极大兴趣， 因为在这些化合物中不包含d或f能带部分填充的常规磁性元素. 虽然很多学者对碱土六硼化物的电子能带结构进行了大量的研究， 但对其体材料电子结构的认知目前仍有很多争论. D. Hall等[6]的费米面测量结果显示CaB6是一种半金属， 而其它诸如角分辨光电子能谱和输运测试结果指出CaB6是一种带隙为1.0 eV左右的半导体[7-8]. 在理论研究方面， 局域密度近似(LDA)的计算结果预言了CaB6， SrB6和BaB6的半金属特性， 在布里渊区的X高对称点上B的能带穿过费米面[9-12]. 而赝势GW计算结果给出CaB6在布里渊区X点上的带隙为0.8 eV[13]. 与此不同的是其它基于轨道线性组合方法(LMTO)的GW计算结果显示不同的带隙值或不存在带隙[14-15]. 最近的屏蔽交换局域密度近似(SX-LDA)给出CaB6是带隙大于1.2 eV的半导体[16].

众所周知， 常规密度泛函理论(DFT)框架下的LDA或广义梯度近似(GGA)方法通常会低估半导体材料的带隙. 本文采用平面波赝势方法(CASTEP)计算包中的杂化HSE06泛函来计算CaB6的电子结构[17-18]. HSE06方法是密度泛函理论最近的一个进步， 对半导体材料来说， 相比于局域或半局域交换关联泛函， HSE06能够得到与实验值符合很好的带隙值[19-20]. 在HSE泛函里用屏蔽的短程Hartree-Fock交换来替代精确Hartree-Fock交换， 交换关联能定义为

式中：a为部分精确交换的贡献； SR和LR分别为交换相互作用的短程和长程部分. CASTEP的HSE06泛函里，a=0.25，ω=0.11.

为了给出更为准确的成键特性及理论光学性质， 本文采用计算能带结构更为精确的HSE06杂化泛函方法研究了CaB6的电子结构， 并与GGA-PBE方法的计算结果进行了比较.

1 计算模型和方法

CaB6晶体的单胞结构如图 1 所示， 属于CsCl型简单立方结构(空间群为Pm3m， No.221)， Ca原子和B八面体分别替代了Cs和Cl的位置， Ca原子位于1a(0,0,0)， 而B原子位于6f(z,0.5,0.5)位置， 其中z为内部参数. CaB6实验测的晶格常数a在4.145 Å～4.153 4 Å范围内， 而内部参数z在0.202～0.207 1范围内[11]. 计算时采用了模守恒赝势， 布里渊区积分采用Monkhorst-Pack形式的K点方法，K点设置为8×8×8. 体系总能量收敛精度为2×10-6eV/atom， 总能量收敛的截断能为900 eV. 计算中没有考虑自旋轨道耦合效应.

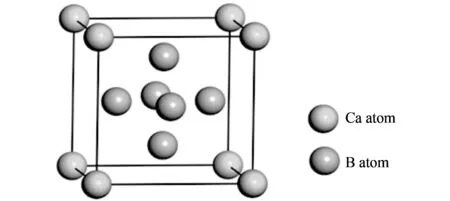
图 1 CaB6单胞结构Fig.1 Bulk structure of CaB6

2 结果与讨论

首先， 为了与其它计算结果对比， 我们在与其它计算中使用的结构(晶格常数a=4.15 Å以及内部参数z=0.207)上进行了计算. 采用HSE06和GGA-PBE方法计算得到的能带结果如图 2 所示， 费米能级位于0.0 eV处.

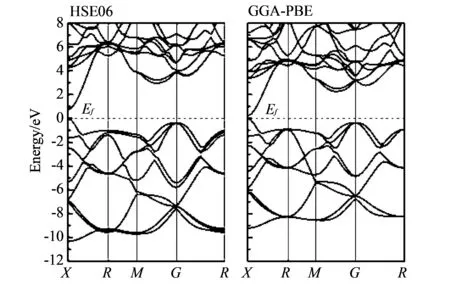
图 2 CaB6电子能带结构Fig.2 Electronic band structure of CaB6

从计算结果看， 在布里渊区X点处， 采用HSE06方法计算得到的CaB6带隙为0.745 eV， 而采用GGA-PBE方法得到的带隙为0.217 eV， 明显小于HSE06方法得到的结果. HSE06的结果与角分辨光电子能谱和输运测试的实验结果以及近期的GW， SX-LDA和加权密度近似法(WDA)计算的结果非常接近[7-8,13,16,21]. HSE06与GGA-PBE方法之间的这种带隙差异是因为HSE06方法中采用了更加精确的交换关联能. 对优化后的结构也进行了计算， 表 1 列出了采用HSE06和GGA-PBE方法计算得到的结果.

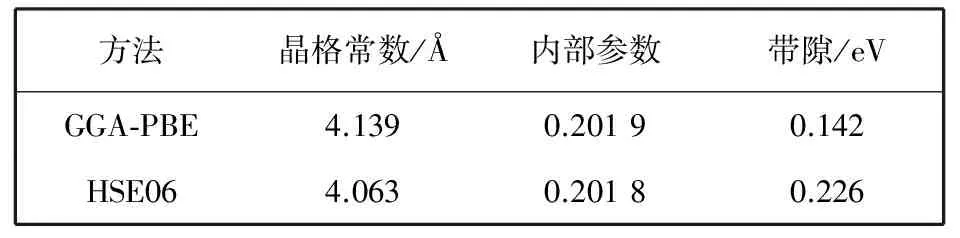
表 1 优化后的结构以及计算得到的CaB6带隙值

从计算结果可以看出， 两种方法在优化结构上计算得到的带隙值比实验结构上的值减小了， 这是因为做结构优化后CaB6的晶格常数变小了. 而GGA-PBE方法做结构优化得到的晶格常数值比HSE06方法更接近实验值. 以上结果表明， 晶格常数值的大小对CaB6的带隙值影响很大. 图 3 中给出了HSE06计算得到的CaB6的总态密度和分态密度图.

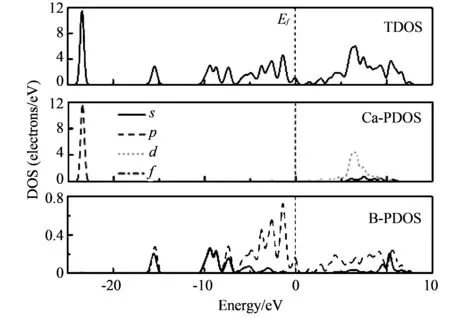
图 3 CaB6的总态密度和分态密度Fig.3 Total and partial density of states of CaB6

从图 3 中可以看出费米面附近的价带主要来自于B的2p态电子的贡献， 而费米面附近的导带主要来自于B的2p态电子和Ca的3d态电子的贡献.

为了弄清Ca和B原子间的成键特性， 对其进行了差分电荷密度和Mulliken电荷布居分析. 图 4 为HSE06计算所得的差分电荷密度图. 在CaB6当中存在两种类型的B键， 连接两个B八面体的键记为BB1， 连接B八面体内相邻B原子的键记为BB2.

图 4 HSE06方法计算的CaB6(110)面的差分电荷密度图Fig.4 Electron density difference at (110) surface of CaB6 from HSE06 method

从图 4 的电荷密度分布图中可以看出， BB1键上的电荷密度大于BB2键上的电荷密度， 说明BB1键强于BB2键. B与B原子间的电荷密度远大于Ca和B原子间的电荷密度， 说明B与B原子间形成共价键， 而Ca与B原子间形成离子键. 表 2 列出了两种方法计算得到的Mulliken电荷布局分析结果得到的从Ca原子转移到B原子的电荷量有一些差别， GGA-PBE得到的结果为 1.74e， 而HSE06得到的结果为 1.87e. Ca的有效离子价态表明CaB6当中离子键和共价键共存， 其中共价特性主要来自于Ca原子的d轨道和B原子的p轨道.

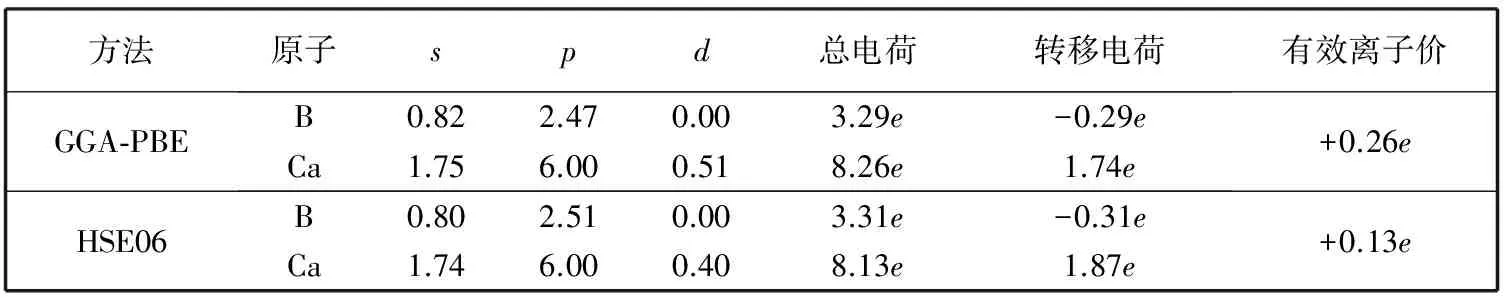
表 2 CaB6的Mulliken电荷布局分析结果

晶体的光学性质通常用介电函数来描述， 从介电函数能够得到能带结构、 带间跃迁和其它光谱信息. 图 5 中给出了两种方法计算得到的CaB6的介电函数虚部与实部的图. 介电函数虚部的峰对应能带中电子的跃迁. 采用GGA-PBE方法得到的介电函数虚部分别在3.9 eV和9.4 eV附近出现了两个比较明显的峰， 其中3.9 eV处的峰对应电子从B的2p态向Ca的3d态的跃迁， 9.4 eV处的峰对应B的2p态的带间跃迁. 而在HSE06的计算结果里这两个峰的位置位于更高能量处， 分别在4.7 eV和11.4 eV处. 这是由于HSE06计算得到的能带相比GGA-PBE方法得到的能带变宽了.

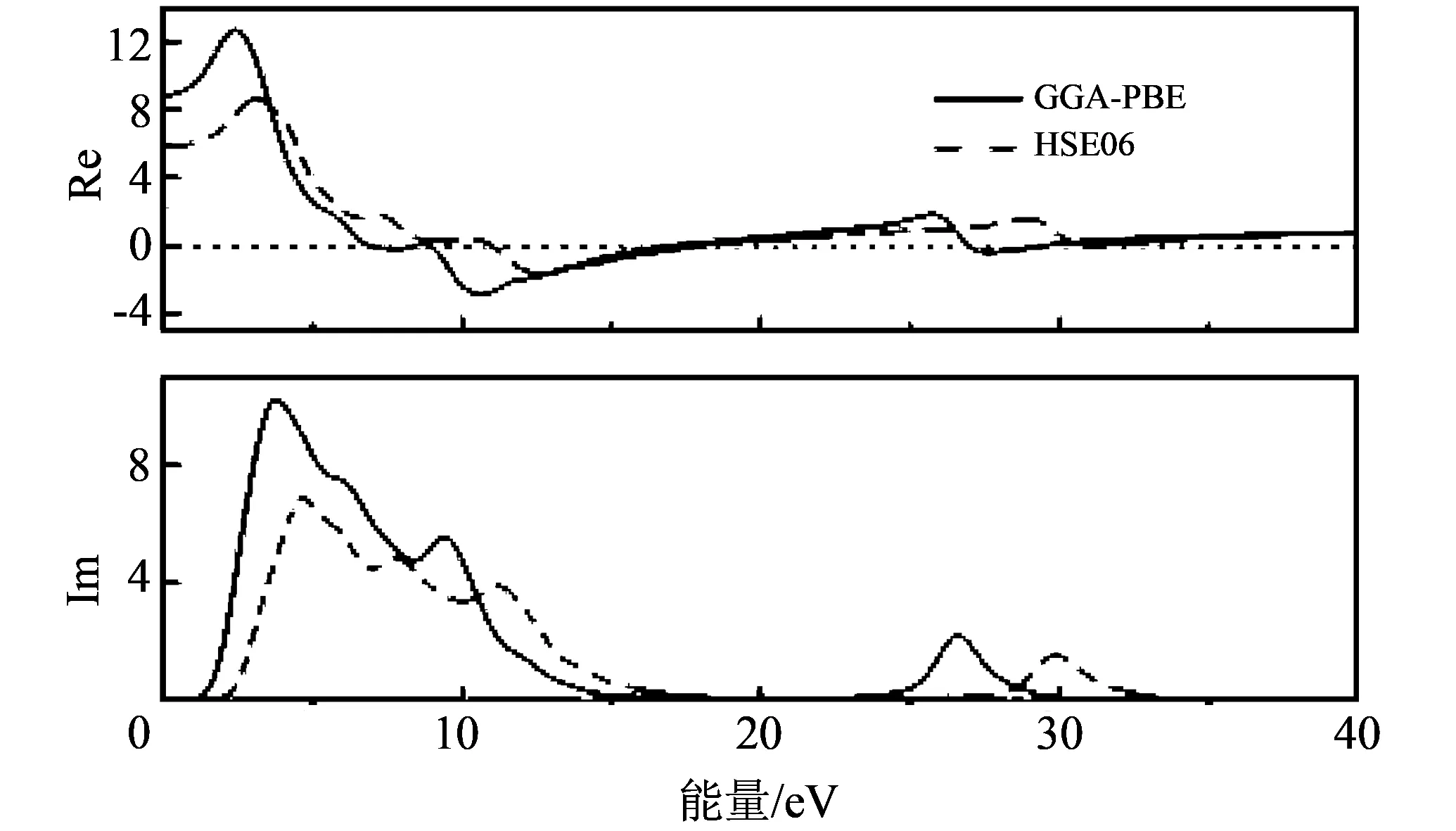
图 5 CaB6介电函数的实部与虚部Fig.5 The real and imaginary parts of the dielectric function for CaB6

3 结 论

本文采用HSE06和GGA-PBE方法研究了CaB6的电子结构、 成键特性以及理论光学性质. 计算结果显示， HSE06和GGA-PBE方法计算得到的实验结构CaB6的带隙值分别为0.745 eV和0.226 eV, HSE06的结果与近期的GW, SX-LDA和WDA方法得到的结果一致， 说明HSE06方法能够得到更合理的CaB6电子结构. CaB6费米面附近的价带主要来自于B的2p态电子的贡献， 而费米面附近的导带主要来自于B的2p态电子和Ca的3d态电子的贡献. Mulliken电荷布局分析表明CaB6当中的BB1键强于其BB2键. HSE06和GGA-PBE方法计算得到的从Ca到B的电荷转移量分别为1.74e和1.87e. 采用GGA-PBE方法得到的介电函数虚部中明显的两个峰分别位于3.9 eV和9.4 eV处， 而在HSE06方法中此两个峰的位置位于更高能量处， 这与HSE06方法中能带变宽有关. 本文研究为理解CaB6的电子结构提供了重要的参考.

参考文献：

[1] Xu T T, Zheng J G, Nicholls A W, et al. Single-crystal calcium hexaboride nanowires: synthesis and characterization[J]. Nano Letters, 2004, 4(10): 2051-2055.

[2] Takeda M, Fukuda T, Domingo F, et al. Thermoelectric properties of some metal borides[J]. Journal of Solid State Chemistry, 2004, 177(2): 471-475.

[3] Ronnebro E, Majzoub E H. Calcium borohydride for hydrogen storage: catalysis and reversibility[J]. Journal of Physical Chemistry B, 2007, 111(42): 12045-12047.

[4] Young D P, Hall D, Torelli M E, et al. High-temperature weak ferromagnetism in a low-density free-electron gas[J]. Nature, 1999, 397(6718): 412-414.

[5] Moriwaka T, Nishioka T, Sato N K. Ferromagnetism induced by Ca vacancy in CaB6[J]. Journal of the Physical Socity of Japan, 2001, 70(2): 341-344.

[6] Hall D, Young D P, Fisk Z, et al. Fermi-surface measurements on the low-carrier density ferromagnet Ca1-xLaxB6and SrB6[J]. Physical Review B, 2001, 64(23): 233105.

[7] Denlinger J D, Clack J A, Allen J W, et al. Bulk band gaps in divalent hexaborides[J]. Physical Review Letters, 2002, 89(15): 157601.

[8] Cho B K, Rhyee J S, Oh B H, et al. Formation of midgap states and ferromagnetism in semiconducting CaB6[J]. Physical Review B, 2004, 69(11): 113202.

[9] Massidda S, Continenza A, Pascale T M, et al. Electronic structure of divalent hexaborides[J]. Zeitschrift für Physik B Condensed Matter, 1996, 102(1): 83-89.

[10] Massidda S, Monnier R, Stoll E. Electronic structure of barium hexaboride[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2000, 17(4): 645-649.

[11] Schmitt K, Stuckl C, Ripplinger H, et al. Crystal and electronic structure of BaB6in comparison with CaB6and molecular[B6H6]-2[J]. Solid State Sciences, 2001, 3(3): 321-327.

[12] Rodriguez C O, Weht R, Pickett W E. Electronic fine structure in the electron-hole plasma in SrB6[J]. Physical Review Letters, 2000, 84(17): 3903-3906.

[13] Tromp H J, Gelderen P, Kelly P J, et al. CaB6: a new semiconducting material for spin electronics[J]. Physical Review Letters, 2001, 87(1): 016401.

[14] Kino H, Aryasetiawan F, Schilfgaarde M, et al. GW quasiparticle band structure of CaB6[J]. Journal of Physics and Chemistry of Solids, 2002, 63(6-8): 1595-1597.

[15] Kino H, Aryasetiawan F, Terakura K, et al. Abnormal quasiparticle shifts in CaB6[J]. Physical Review B, 2002, 66(12): 121103.

[16] Lee B, Wang L W. Electronic structure of calcium hexaborides[J]. Applied Physics Letters, 2005, 87(26): 262509.

[17] Clark S J, Segall M D, Pickard C J, et al. First principles methods using CASTEP[J]. Zeitschrift für Kristallographie-Crystalline Materials, 2005, 220(5/6): 567-570.

[18] Heyd J, Scuseria G E, Ernzerhof M. Hybrid functionals based on a screened coulomb potential[J]. Journal of Chemical Physics, 2003, 118(18): 8207-8215.

[19] Hummer K, Harl J, Kresse G. Heyd-scuseria-ernzerhof hybrid functional for calculating the lattice dynamics of semiconductors[J]. Physical Review B, 2009, 80(11): 115205.

[20] Kim Y S, Hummer K, Kresse G. Accurate band structures and effective masses for InP, InAs, and InSb using hybrid functionals[J]. Physical Review B, 2009, 80(3): 035203.

[21] Wu Z G, Singh D J, Cohen R E. Electronic structure of calcium hexaboride within the weighted density approximation[J]. Physical Review B, 2004, 69(19): 193105.