基于犹豫模糊互补偏好的PPP融资模式选择群决策研究

李彦华， 杨星宇， 牛 蕾， 张月婷

(中北大学 经济与管理学院， 山西 太原 030051)

0 引 言

随着中国经济的迅速崛起， 对基础设施项目的投资需求呈现爆发式增长. PPP融资模式作为一种有效吸引私人资金和技术的创新性融资模式， 也于近十几年在中国迅速发展起来. 目前关于PPP融资模式选择方面的研究众多， 主要集中在PPP融资模式分类、 PPP指标选取以及模式选择方法， 其中关于模式选择方法的研究集中在层次分析法、 实物期权法以及多属性群决策法. 由于层次分析法一致性检验难度较大且缺乏理论依据、 易忽略专家权重； 实物期权法存在模型风险， 模型参数假设的准确性受到质疑， 因此， 本文采取多属性群决策法来进行PPP融资模式的选择研究. Chang针对风险分担机制不合理与契约不完善的问题， 通过构建多属性分析模型选择出合适的项目融资模式[1]. Cheung通过问卷调查方法对项目融资模式的效用计值， 并利用多属性的效用分析选择出合适的融资方案[2]. Chan和Oyetunji在Cheung的研究基础上提出了使用摇摆赋权多属性评价方法来选择PPP融资模式[3-4]. 杨亚楠通过综合运用案例研究以及多属性群决策对PPP融资模式进行选择[5]. 卢智琪依据项目特点构建融资模式选择的评价指标体系， 在此基础上构建多属性群决策模型选择出合适的PPP融资模式[6].

从国内外研究进展中可以看出， 经过多年实践， 基于多属性群决策的PPP融资模式选择方面的研究已经取得了一定成果， 尤其是指标的选取以及指标和专家权重确定方面成效斐然， 但现有研究由于对过程中的决策个体在进行项目选择时存在的主观性、 变动性以及对犹豫性的考虑不充分， 会对最终决策结果的合理性造成影响. 因此， 本文将决策参与者模糊思维方式和协商讨论加入到决策过程， 采用犹豫模糊互补偏好矩阵来表达专家偏好信息， 在考虑多方影响因素的基础上对PPP项目融资模式的选择决策进行研究.

1 PPP项目融资模式选择群决策模型的原理及步骤

犹豫模糊互补偏好是犹豫模糊集理论和模糊互补偏好相结合的产物[7]. 由于PPP项目在融资模式选择过程中受到诸多因素的影响， 单个简单的数值不足以表示专家决策的信息. 与此同时， 由于决策过程中的各个专家的社会背景以及专业背景存在差异， 以及人类在作决策时犹豫的特点， 所以， 本文采用犹豫模糊互补偏好矩阵表示专家的决策信息， 并在相关指标体系基础之上构建PPP项目融资模式的群决策模型， 在客观灵活反映决策信息的同时， 兼顾了决策方案选择的准确性. 文中建立的群决策模型主要分为两个部分：专家共识衡量、 专家共识调整和方案选择， 具体如下.

1.1 犹豫模糊互补偏好关系专家共识衡量

(1)

本文建立的群决策模型是基于专家共识的决策， 专家共识的衡量是本模型中的一个重要问题， 本文运用距离来衡量决策个体与群体之间的偏差. 个体偏好与群体偏好之间的偏差指标定义如下：

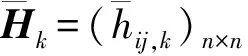
(2)

1.2 犹豫模糊互补偏好关系专家共识调整

专家共识的调整是群决策共识研究中的重要部分， 与共识衡量共同组成了共识研究的主体架构. 本文运用距离来衡量个体与群体之间的偏差， 运用加权平均算法得到群体共识指标， 并将其与设定好的阈值比较， 若其大于阈值， 表示专家群体没有达成共识， 需要做进一步的调整， 使其达到可接受的阈值范围. 在共识调整过程中， 在保留尽可能多的原始专家偏好信息的同时， 要使得计算过程尽可能简单、 科学可靠. 因此， 本文对专家权重和专家偏好两方面同时调整， 在减少迭代时间的同时兼顾了原始信息的保留. 具体流程见图1， 具体调整算法如下：

步骤 4： 计算群共识指标θ(t)， 若θ(t)≤δ， 则表示群体决策达到共识水平， 进行步骤 7； 否则， 进行步骤 5；

(3)

式中：k∈E{z}表示k∈E， 但k≠z；n为方案个数. 计算专家ez关于方案ai的贡献水平Diz为

(4)

式中：Ci为关于方案ai的共识指标.

计算专家ez对全部方案的贡献程度Dz为

(5)

式中：Dz值越大， 表明该专家在群决策共识研究中的贡献越大， 若Dz>0， 表明该专家起积极作用， 若Dz<0， 表明该专家起着消极作用， 为了减少其消极作用， 将降低其权重.

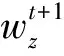
(6)

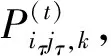
(8)

其中，i,j=1,2,…,n;k=1,2,…,m.

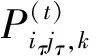
(9)

设t=t+1， 返回第3步.

(10)

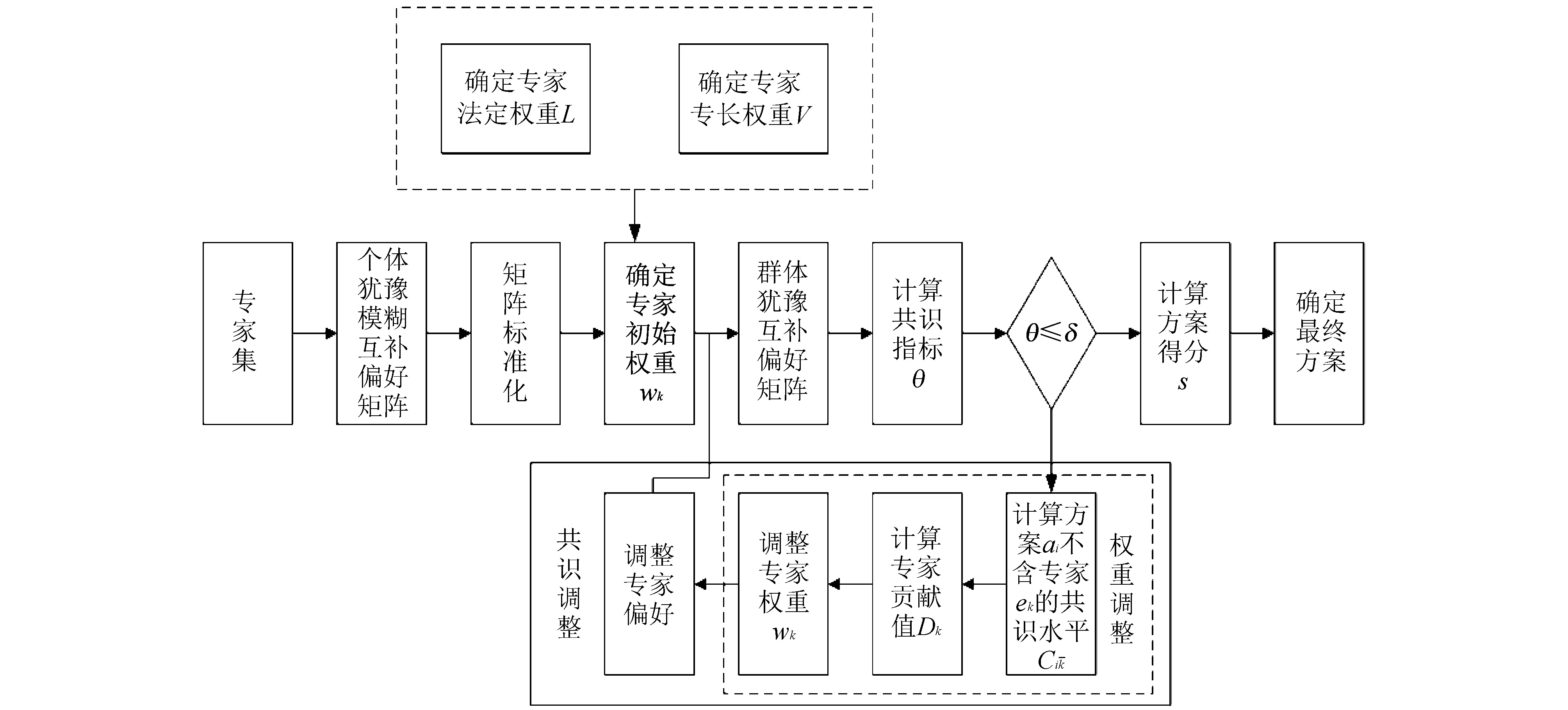
图 1 决策模型流程图Fig.1 The flow chart of decision model

2 PPP融资模式选择决策指标体系构建

2.1 PPP融资模式选择影响因素

PPP项目在选择融资模式的过程中， 在考虑项目自身经济特征的同时， 也要考虑融资模式的适用性， 各种不确定因素所带来的风险， 以及操作的复杂性等诸多因素. 因此， 根据PPP项目的具体情况， 在此将PPP融资模式选择的影响因素分为经济性因素、 适用性因素、 风险性因素和复杂性因素.

经济性因素是PPP项目融资模式选择过程中最为重要的影响因素， 主要包括资金来源的可靠性和融资交易成本. 资金来源的可靠性是指PPP项目获得资金的困难程度. 在PPP项目的筹建过程中， 因为资金不能及时到位而影响项目进程事件时有发生， 因此， 在对融资模式做出最后的选择之前， 对资金的可获性进行分析是非常有必要的. 融资交易成本是指为筹集PPP项目的所需资金而付出的费用[8]. 不同的融资模式因为操作程序的差异而造成了交易成本的差异. 融资交易成本在很大程度上影响着项目融资模式的选择， 是PPP项目融资模式选择过程中一个需要重点考量的因素.

适用性因素包括融资模式适用范围的匹配性以及融资模式现阶段的可操作性[9]. 融资模式适用范围的匹配性主要是指项目融资模式与项目本身的匹配程度. 融资模式与项目匹配程度的高低会对项目收益造成很大的影响. 融资模式现阶段的可操作性主要是指现阶段中国对于采用某种融资模式为PPP项目融资的操作是否符合相关法律法规， 是否可以得到政府的扶持， 以及目前中国金融市场的发展完善程度是否支持该操作.

风险性因素包括金融性风险和市场需求风险[10]. 金融性风险是指对在融资过程中由于各种外部环境变化而增加项目融资成本从而造成项目财务危机的风险. 财务危机的发生会给项目造成极大的损失， 因此金融风险是选择融资模式时需考量的关键因素. 市场需求风险主要源于市场需求主体偏好的变化而造成的项目收益不确定. 市场需求风险直接影响项目的实际收益， 选择融资模式时需要考虑项目的市场需求风险.

复杂性因素主要包括融资运作程序的复杂性和经营所有权转让的复杂性. 融资运作程序的复杂性是由不同融资模式的融资结构的差异性造成的. 融资运作程序的复杂程度会影响融资的资金成本的高低， 复杂程度越高融资所需的资金成本就越高[11]. 大多数PPP融资模式因为特许经营期的存在都会涉及到经营权的转让问题， 例如BOT模式和TOT模式. 若经营所有权转让手续复杂程度比较高， 项目融资的各种成本都会相应的增加， 从而影响项目的效益[12].

2.2 指标的选择

根据现阶段中国PPP项目融资模式的特征以及PPP项目融资模式选择的影响因素， 结合PSC评价指标体系， 本着科学性、 实用性、 全面性和代表性的原则， 建立了PPP项目融资模式选择指标体系， 详细见表 1.

表 1 PPP项目融资模式选择指标体系

3 算例分析

为方便某两座城市之间人员的相互往来， 加强两地经济文化的交流， 政府采用PPP模式建设城际铁路. 该项目采用“投资+融资+建设+维护管理”的PPP建设模式. 线路长度13.186 km， 高架线11.507 km， 地下段0.991 km， 地面段 0.688 km， 车站8座， 其中高架站7座， 地下站1座， 车辆段1处， 车辆段出入线1.26 km. 项目建设内容包含高架和盾构区间、 轨道工程、 车辆段及出入线. 建设投资约23.41亿元. 现有3个PPP方案可供选择， 其中， 各方案包含了出资比例、 特许经营权期限、 收益分配等内容， 融资模式选择的PPP融资模式方案集为A={a1,a2,a3}. 为了合理、 准确地选择最优PPP方案， 邀请了5位相关专家E={e1,e2,e3,e4,e5}对3个方案进行经验判断. 本文采用德尔菲法确定各个专家的职位关联度， 采用多关键词匹配算法确定专长关联度， 依据文献[13]中的方法进而确定各个专家的法定权重、 专长权重以及初始权重. 具体结果见表 2.

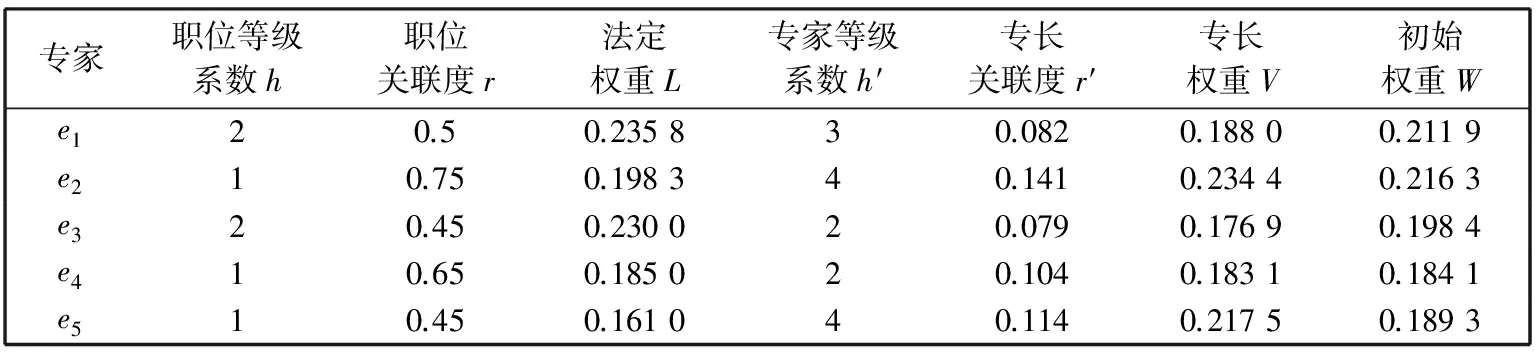
表 2 专家群体的权重

决策者依据融资模式选择指标体系对该PPP基础设施项目的融资模式选择方案进行评价， 得出各自的犹豫模糊互补判断矩阵， 设η=0.5，β=1.5， 共识阈值δ=0.05. 得到的每位专家ek犹豫模糊互补判断矩阵Hk如下， 其中k=1,2,3,4,5.

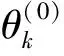
表 3 方案共识指标值

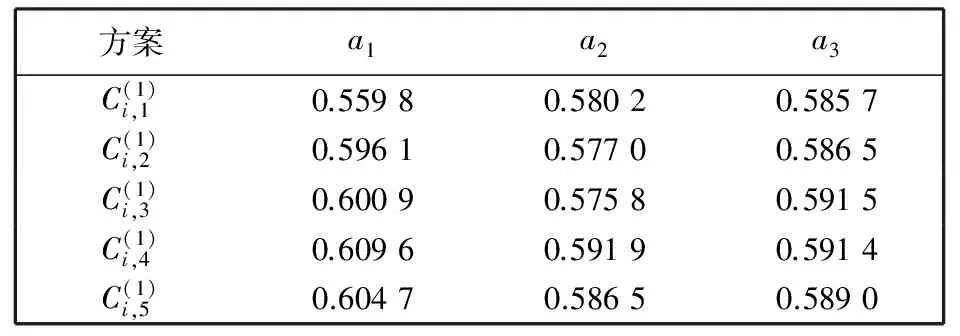
表 4 方案不包含特定专家的共识指标值

表 5 专家贡献值

表 6 调整后专家权重值

表 7 偏差最大元素及调整值

令t=t+1， 返回步骤2继续进行迭代调整.

经过3次迭代后， 最终的群共识指标θ(3)=0.044 9<0.05， 表明可以接受当前的群共识指标， 迭代结束. 依据式(15)计算各方案的得分， 结果如下

s(a1)=1.035 6,s(a2)=1.084 0,

s(a3)=1.067 0.

因此方案之间排序为：a2≻a3≻a1， 其中a2为最优方案.

4 结 论

本文考虑到决策者在制定决策过程中的模糊性等因素， 用犹豫模糊互补偏好矩阵来表达各个专家决策信息， 从PPP项目融资模式的经济性、 适用性、 风险性以及复杂性出发， 构建融资模式选择指标体系； 为使初始专家权重更加的客观合理， 通过专家法定权重和专长权重结合的方法确定各个专家的初始权重； 为了保证最终决策方案的科学性和合理性， 模型采用专家调整权重和专家偏好调整同时进行的方法来进行专家共识的调整. 首先通过减小贡献度较低的专家权重的方法来调整决策专家权重， 进而提高决策群体的共识水平； 其次， 对专家偏好与群体偏好差值最大的元素进行专家偏好调整. 与以往单独采用权重调整或偏好调整的方法相比， 本文采用的两种方法并行结合的模型， 不仅可以使得原始信息得到尽可能的保留， 而且可以很大程度上减少迭代的时间， 以高效合理的方式达成专家共识. 算例表明， 该方法能为PPP项目融资模式方案选择提供有效的决策支持， 为基础设施建设的顺利展开打下良好基础.

参考文献：

[1] Chang C, Ive G. Rethinking the multi-attribute approach based procurement selection technique[J]. Construction Management and Economics, 2002, 20(3)： 275-284.

[2] Cheung S O, Lam T I, Wan Y W,et al. Improving objectivity in procurement selection[J]. Journal of Management in Engineering, 2001, 17(3)： 132-139.

[3] Chan A P C, Yung E H K, Lam P T I, et al. Application of Delphi method in selection of procurement systems for construction projects[J]. Construction Management & Economics, 2004, 19(7)： 699-718.

[4] Oyetunji A A, Anderson S D. Relative effectiveness of project delivery and contract strategies[J]. Journal of Construction Engineering & Management, 2006, 132(1)： 3-13.

[5] 杨亚楠. 基于多属性决策的PPP(Public-Private Partnerships)模式选择研究[D]. 大连： 大连工业大学， 2013.

[6] 卢智琪. 基于多属性群决策方法的污水处理项目融资模式选择研究[D]. 大连： 东北财经大学， 2015.

[7] 刘霞， 吴楠楠， 许叶军. 基于犹豫模糊互补偏好的水资源配置群决策研究[C]. 中国管理科学与工程学会. 管理科学与工程学会2016年年会论文集. 镇江： 江苏大学出版社， 2016： 262-271.

[8] 汤薇， 吴海龙. 基于政府角度的PPP项目融资效益研究——以BOT与BOO模式为例[J]. 科研管理， 2014， 35(1)： 157-162.

Tang Wei， Wu Hailong. Research on PPP project financing efficiency from government perspective—Taking BOT and BOO modes as examples[J]. Science Research Management， 2014， 35(1)： 157-162. (in Chinese)

[9] 戴丽琼. 基于AHP的城市污水处理融资模式分析[J]. 陕西科技大学学报(自然科学版)， 2011， 29(1)： 99-105.

Dai Liqiong. Analysis of financing mode in the urban sewage treatment based on analytic hierarchy process[J]. Journal of Shaanxi University of Science & Technology(Natural Science Edition)， 2011， 29(1)： 99-105. (in Chinese)

[10] 亓霞， 柯永建， 王守清. 基于案例的中国PPP项目的主要风险因素分析[J]. 中国软科学， 2009(5)： 107-113.

Qi Xia， Ke Yongjian， Wang Shouqing. Analysis on critical risk factors causing the failures of China’s PPP projects[J]. China Soft Science， 2009(5)： 107-113. (in Chinese)

[11] 朱秀丽， 邱菀华. 基于实物期权的铁路地下化项目PPP模式投资决策分析[J]. 系统工程， 2011, 29(3)： 117-120.

Zhu Xiuli， Qiu Wanhua. Analysis of investment decision in railway underground PPP Project based on real option[J]. Systems Engineering， 2011, 29(3)： 117-120. (in Chinese)

[12] 李露凡， 舒欢. 基于模糊综合评价模型的工程项目融资模式评价与决策[J]. 工程管理学报， 2014, 28(3)： 104-108.

Li Lufan， Shu Huan. The evaluation and decision of project financing model based on fuzzy comprehensive evaluation model[J]. Journal of Engineering Management， 2014, 28(3)： 104-108. (in Chinese)

[13] Daft R L. Management[M]. Boston： South-Western College Press， 1998.