复杂网络视角下供应链网络模型研究

丁 飞， 陈 红

(中北大学 创新研究中心, 山西 太原 030051)

0 引 言

供应链网络， 是指通过资源、 战略、 能力等方面的共同协作， 由供应商、 制造商、 分销商和零售商等众多成员厂商组成的复杂供应-制造-销售网络[1]. 全球经济一体化的深入， 使供应链网络已经由传统的链式结构发展为复杂的网络结构. 而复杂网络作为目前国内外最前沿的系统理论， 对于解决非线性、 混沌、 不确定复杂问题具有独特的优势[2].

目前， 运用复杂网络研究供应链网络已经引起了学者们的关注. 在供应链网络的特性方面， 大量文献研究表明， 供应链网络具有适应性、 无标度性和鲁棒性. Marchi等[3]构建适应性供应链网络演化模型， 研究了供应链网络的自适应性. Kühnert 等[4]对城市的物资供应网络进行分析， 发现该网络服从无标度分布. 李彬等[5]构建了基于供需能力的供应链网络鲁棒性模型， 研究了无尺度型供应链网络在随机失效和蓄意攻击下的鲁棒性.

在供应链网络演化机制的设计方面， 学者们采用Petri网[6]、 Agent建模[7]、 博弈[8]和复杂网络中的BA模型等方法， 对供应链网络的演化问题进行研究. Barabási等[9]提出BA演化模型， 该模型遵循两个基本演化机制:“增长”和“择优连接”. 自BA模型被提出之后， 学者们开始广泛采用BA模型对供应链网络进行深入研究. 曹文彬等[10]提出企业间通过合作带来的边效益的概念， 以此作为择优连接的测度指标. 丁青艳[11]构建了基于度与交易成本连接的供应链网络演化模型. 在对节点进入机制研究的基础上， 学者们还研究了节点的退出行为. 谢珊珊[12]考虑了节点进入与退出网络的情形， 并对其进行建模仿真. 但是学者们在研究退出行为时， 普遍假设节点与网络内其他节点的连接是同时中断的， 也就是“随即退出”， 并不符合节点退出时与其他节点逐步断开连接的过程. 同时， 学者们对于节点之间连接的断开， 大多会随机选择n条连接将其断开， 但在现实网络中， 度值越大的节点， 其拥有的连接越不容易丢失， 因此本文引入了反择优连接概率来研究节点的退出行为.

本文在BA模型的基础上将上述实际问题考虑进来， 构建基于节点进入、 退出和合作机制下的供应链网络演化模型， 从仿真模拟和实证分析两方面验证模型的合理性.

1 供应链网络复杂性分析

供应链网络既体现了供应链的动态性和网络性， 又体现出复杂网络的一般性.

1.1 核心厂商的高集聚性

在供应链网络中， 会产生少数核心厂商， 其他的厂商依赖核心厂商而存在. 少数核心厂商有着巨大的的市场优势， 其进入或退出网络， 都将影响到供应链网络的现有结构. 依据市场竞争的原则， 网络中存在的厂商将会优先选择具有竞争优势的厂商作为合作伙伴， 造成“富者愈富”的现象[13]. 因而， 供应链网络具有核心厂商的高集聚特征， 即少数节点具有较大的度.

1.2 网络拓扑关系的高度动态性

供应链网络中的每个厂商具备一定的适应能力和学习能力[14]. 在彼此的竞争中， 各厂商遵循优胜劣汰原则， 每个厂商都会进行自我适应和不断学习， 在这个过程中， 能力强的厂商则会不断的发展壮大， 而能力弱的厂商会被淘汰， 或是被新的厂商所取代. 因而， 供应链网络的结构关系呈现出复杂的动态性.

1.3 遵循幂律分布

供应链网络具有无标度特性， 其度分布遵循幂律分布， 即供应链网络中存在度值很大的厂商. 这里度值是指与该厂商相连的厂商的边的数目， 或是与该厂商相邻的厂商数目. 如汽车供应链网络[15]、 B2C电商供应链网络[16]和轿车供应链[17]等都表现出相应的幂律分布.

根据上述分析， 供应链网络同时具有供应链和复杂网络的特征， 因而可以将供应链网络看作复杂的网络系统， 用复杂网络方法去探究供应链网络的演化机理， 进而分析供应链网络的演化机制.

2 供应链网络演化模型的建立

2.1 供应链网络演化规则

本文将供应链网络中的每一个厂商主体视为复杂网络中的“节点”， 而将厂商间的各种合作关系视为复杂网络中的“边”. 厂商之间通过信息流、 物流和资金流来实现相互间的合作关系， 从而形成了一个复杂的供应链网络[18]. 为了更好地理解供应链网络的演化机制， 本文从节点厂商所表现出的竞合关系入手， 研究供应链网络中厂商进入、 退出和合作行为.

本文以BA模型为基础， 考虑节点进入、 退出与合作行为， 依据供应链网络演化特征， 进而提取出供应链网络演化规则.

2.1.1 增长规则

供应链网络有效整合了分散的资源和技术， 具备相应的经济效应和集群优势， 会吸引大量厂商加入网络， 与网络中的其他厂商建立不同类型的合作关系[19]. 所以网络内各厂商数量会不断变化， 厂商间的连接也呈现出动态增长趋势， 进而促进供应链网络的演化.

2.1.2 择优连接规则

进入供应链网络的新厂商在选择合作伙伴时， 遵循择优连接规则， 新厂商愿意选择供应链网络中拥有较多合作关系的核心厂商进行合作， 即优先与节点度值大的节点建立连接， 连接概率正比于目标节点的度.

2.1.3 合作规则

供应链网络内部的厂商与其他厂商之间总是在不断地建立新的合作连接， 发生各种各样的联系[20]， 该连接也遵循择优连接， 最终使得网络中的连接数逐渐增多， 网络规模逐渐变大.

2.1.4 退出规则

由于供应链网络中各厂商间存在的激烈竞争， 导致一些厂商的生存压力变大， 会选择或被迫解除彼此间的合作连接， 即网络内节点连接出现断裂， 从而退出网络. 原来学者们研究节点的退出行为时， 大都认为节点是同时断开与其他节点的连接. 但在现实网络中， 节点的退出行为并不是随即的， 而是一个逐步断开与其他厂商连接的过程. 所以本文假设节点是逐渐退出的， 且当厂商与供应链网络内的其他所有厂商都没有合作连接时， 可以认为该厂商已经从供应链网络中退出.

2.1.5 反择优断开规则

以往学者们研究供应链网络内节点厂商的退出行为时， 会随机选择n条连接将其断开. 但在现实网络中， 某些度值大的节点越有竞争优势， 与之合作的其他节点越不会终止二者之间的联系， 断开其连接， 因而这些度值大的节点所拥有的连接越不容易被断开. 而那些自身能力弱的节点， 由于生存压力较大， 常常会成为其他节点终止合作的选择对象. 所以本文在研究节点退出时， 节点之间连接的断开遵循反择优规则， 即度值越大的节点， 其拥有的连接越不容易丢失.

2.2 供应链网络演化算法

在厂商进入供应链网络的过程中， 本文假设在每个时间步长里， 只有一个新厂商进入. 进入到供应链网络中的厂商要与供应链网络中已有的多个厂商发生连接， 本文假设每个新厂商与供应链网络中的m个厂商发生连接， 且新进入的厂商依据择优连接规则， 即每个新增连接以正比于目标节点度的比例与目标节点发生连接.

在厂商逐渐退出供应链网络的过程中， 即网络中的连接逐渐断开时， 本文假设在每个时间步长里， 以反择优概率断开n条连接.

在供应链网络内部， 各个厂商间总是在不断地建立新的合作连接， 该连接也遵循择优选择.

根据上述分析， 本文提出综合厂商进入、 退出和合作机制的供应链网络演化模型， 具体的算法为：

开始于m0个孤立节点厂商， 并且在每个时间步长里， 有下列3种情况发生：

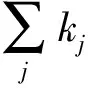
(1)

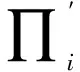
(2)

式中：N(t)为网络内节点的个数， 即N(t)=t+m0.

3) (合作连接)在网络内增加r条新边， 这些边与节点i的合作也遵循择优连接， 即新边的两个端点均以择优概率∏i被选取.

这3种情况解释了供应链网络中厂商进入、 退出与合作的过程. 随着时间的演化， 在这3种机制的作用下， 供应链网络逐渐发展成为复杂网络.

3 模型仿真分析

本文运用MATLAB工具模拟供应链网络的演化生成过程， 设定参数m0=5,m=2,n=1,r=1， 待网络内的节点数量N=100时停止演化， 即网络从5个初始节点开始演化. 之后分别从网络的拓扑结构、 度分布、 平均度、 平均最短路径和集聚系数等统计特征方面研究供应链网络的演化特征.

3.1 拓扑结构

图 1 所示为节点数量达到25, 50, 75, 100时， 供应链网络演化仿真的拓扑结构状态.

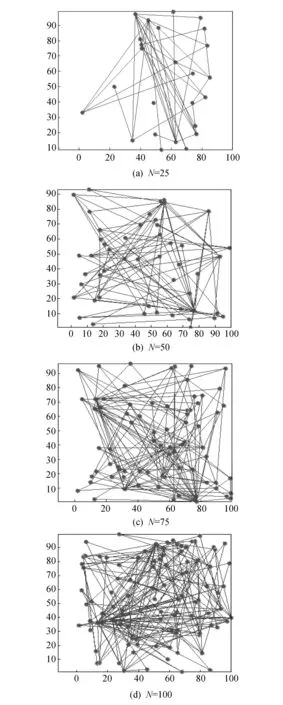
图 1 供应链网络动态演化拓扑图Fig.1 The dynamic evolution of supply chain network topology

在图 1(a) 中， 网络中拥有25个节点， 厂商数量较少， 这25个厂商借助自己上下游的制造商、 零售商等， 形成了单链供应链. 厂商彼此之间都有相应的了解， 也存在少量的合作， 此时供应链网络正处在初期的筹备组建阶段.

在图1(b)中, 总是有新的厂商进入网络内， 选择与那些竞争优势强的厂商进行合作， 此时网络处于高速发展期.

在图1(c)中, 网络内的节点数量达到75个， 这些厂商之间的合作连接仍在不断的增长， 但也有少量企业因压力选择退出网络.

从图1(d)中可以看出， 网络规模仍在不断的扩大. 但随着仿真过程的深入可以看出， 有的节点拥有的连接数很多， 而有的节点的连接数则很少， 说明网络已经呈现出无标度的特征.

3.2 度分布

在复杂网络中， 通常用ki来代表节点i的度， 它指的是和该节点连接的其他节点的数量. 节点的度分布p(k)被定义为任意选取某一个节点， 其度值恰好为k的概率， 等于网络中度值为k的节点的数量占网络节点总数量的比值.

在供应链网络演化仿真的过程中， 对网络内各厂商节点度进行统计， 得到各节点度的直方图. 如图 2 所示， 一方面， 网络中出现少数节点度值较大的节点， 其度值达到28左右， 这表明在供应链网络中存在少数核心节点， 与其他节点相比， 他们在市场中占据较大的竞争优势， 与众多的厂商发生业务联系. 当这些核心节点退出网络时， 会对整个网络的性质和结构带来巨大的影响.

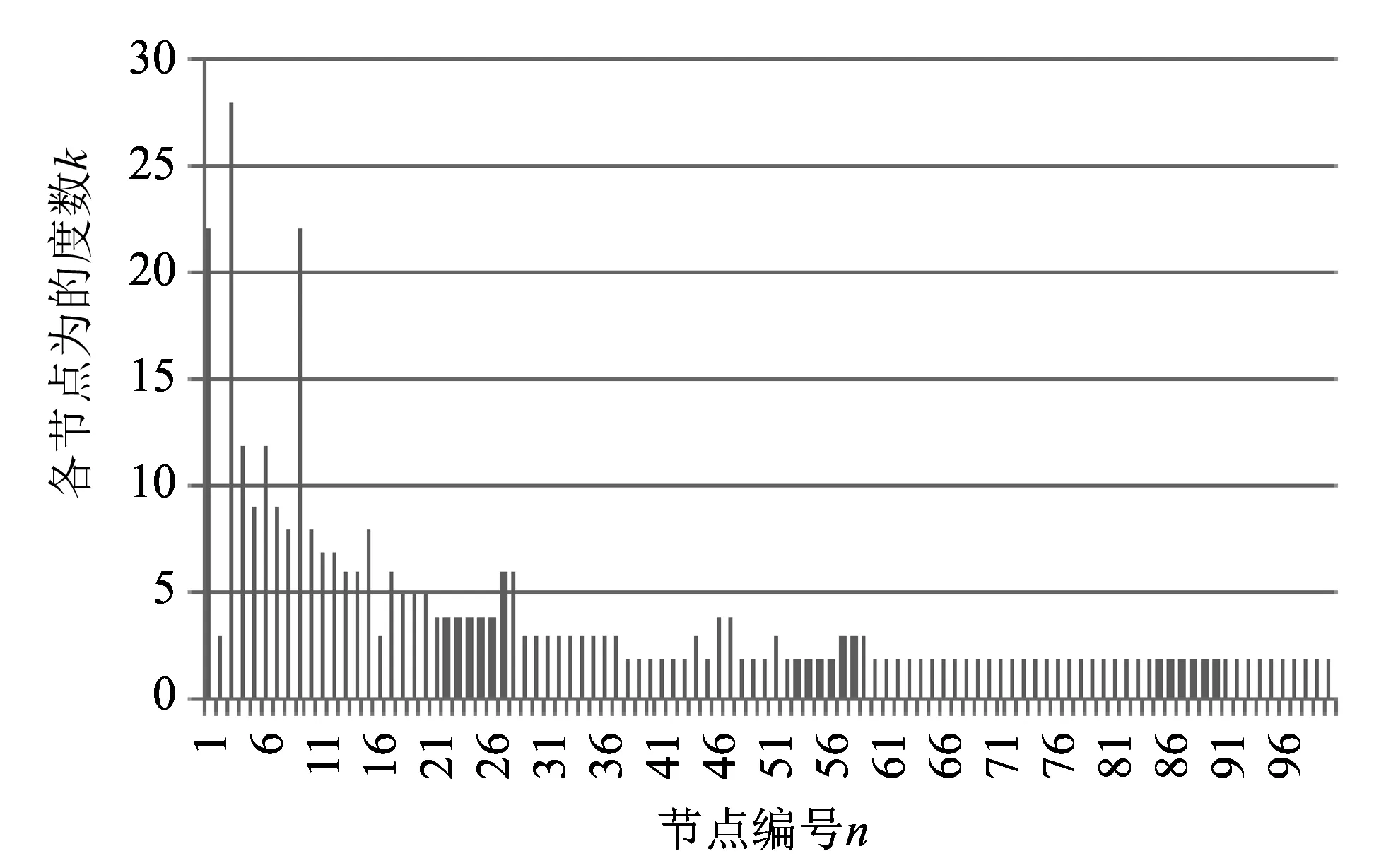
图 2 节点度的大小分布图(N=100)Fig.2 Node degree distribution(N=100)

另一方面， 大多数节点的度值都较小， 这表明供应链网络中的大部分厂商都只是与很少的厂商发生业务联系.

同时， 在MATLAB中对节点的度进行幂率分布拟合， 得到度分布拟合曲线如图 3 所示， 其中横坐标x表示度值k, 纵坐标y表示概率p(k). 拟合结果得到幂率分布的指数γ为2.851， 可决系数R-square为0.991 1， 说明拟合效果较好. 所以， 本文构建的供应链网络度分布服从幂率分布， 属于无标度网络.

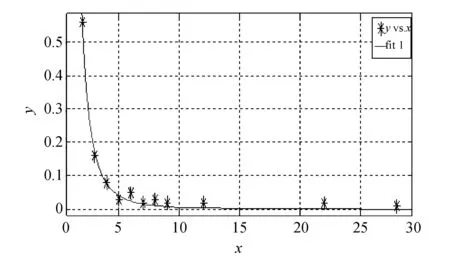
图 3 节点度分布拟合曲线(N=100)Fig.3 Node degree distribution fitting curve(N=100)

3.3 平均度

平均度， 指所有节点度的平均值， 实际指网络的紧密程度， 即节点之间连接的数量. 其理论公式为

(3)

图 4 平均度与网络规模N的关系Fig.4 The relationship between average degree and network size N

从图 4 可以看出， 随着网络规模N的增加， 平均度〈k〉逐渐增加， 且增加的速度越来越小， 最终稳定在3.8左右， 说明在本文的供应链网络中， 每一个厂商平均与3个左右的厂商发生合作关系. (其中每个点为MATLAB进行10次仿真后所取结果的平均值)

3.4 平均最短路径

平均最短路径L， 指各个节点间距离的平均值， 能够用来衡量一个网络的效率和传递性能. 实际意义是指信息从一个节点到另一个节点所经过的平均最少的节点个数. 一般来讲， 平均最短路径越小， 越会加快网络内部物流和信息的流动， 即网络传输效率越快. 其理论公式为

(4)

式中：dij为节点i和节点j之间的距离.

从图 5 中可以看出， 随着网络规模N的增加， 平均最短路径L呈现出逐渐上升的趋势， 但当网络规模越大时，L上升速度越缓慢， 因而L与N的对数值之间为线性关系， 即L～log(N)， 这说明供应链网络具有小世界特性. 同时，L的取值大多分布在2.5～3之间， 即在本文的供应链网络中， 节点与节点之间合作关系的完成要经过2～3个节点， 说明该网络的传输效率较高， 响应速度较快.

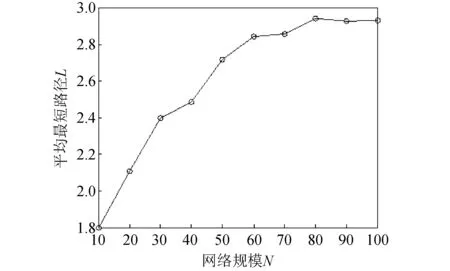
图 5 平均最短路径L与网络规模N的关系Fig.5 The relationship between the shortest path L and network size N

3.5 集聚系数

网络的集聚系数C， 能够用来衡量网络中各个节点的聚集情况， 进而反应出一个网络的集聚特征. 一般来讲， 若节点i与其他ki个节点相互连接， 在完全理想的状态下， 这ki个节点之间最多可以建立ki(ki-1)/2条边， 但考虑到现实情况，ki个节点之间实际存在的边的数目为Ei条. 节点的集聚系数Ci被定义为Ei与ki(ki-1)/2的比值， 其理论公式为

(5)

网络的集聚系数C为网络中各个节点的集聚系数Ci的平均值.

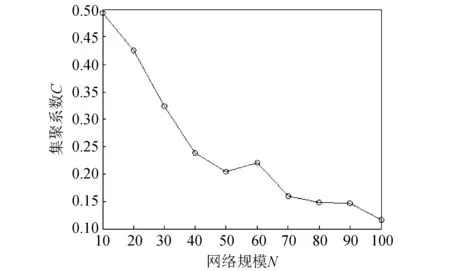
图 6 集聚系数C与网络规模N的关系Fig.6 The relationship between the cluster coefficient C and network size N

从图 6 中可以看出， 随着网络规模N的增加， 集聚系数C呈现出逐渐减少的趋势， 由0.49下降至0.1左右， 且网络规模越大， 下降速度越缓慢. 该仿真结果与理论结果一致， 说明仿真模型是正确可行的.

4 实证分析

4.1 数据来源

在我国汽车工业集团中， 一汽集团占据较大的市场份额， 因而其供应链网络数据有较好的代表性. 所以参考《中国汽车工业年鉴2016》， 选取了一汽集团2015年度的主要整车、 发动机制造厂股比数据数据， 用来验证本文之前构造的供应链网络模型的合理性.

4.2 实证网络分析

4.2.1 实证网络的拓扑结构

本文使用pajek软件得到一汽供应链网络的拓扑结构， 如图 7 所示. 在图 7 中， 共有44家企业， 彼此之间存在着复杂的供需关系.

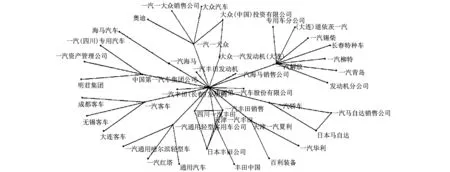
图 7 一汽供应链拓扑结构Fig.7 Supply chain topology of yiqi

4.2.2 实证网络的度分布

通过pajek软件得到一汽供应链的度分布， 对其进行幂率拟合， 结果如图 8 所示， 其中， 拟合后的幂率指数为1.892， 可决系数R-square为0.969 8， 说明拟合效果较好， 一汽网络的度分布属于幂率分布.

在图 8 中可以看出， 任取一个节点， 度小于或者等于3的概率为81%， 度大于3的概率仅仅为18%. 假如在该网络中以度3作为分界点， 若某一个节点的度大于3， 则称该节点为度比较大的节点， 若某一个节点的度小于或者等于3， 则称该节点为度比较小的节点. 在该网络44个节点中， 有8个节点属于度比较大的节点， 占全部节点数的18%； 有36个节点属于度比较小的节点， 占全部节点数的82%， 因此可以得出结论， 一汽网络中存在少数核心节点， 满足复杂网络无标度的特性.

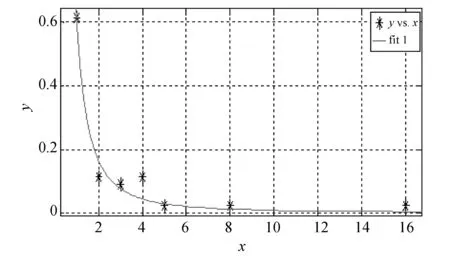
图 8 一汽供应链节点度分布拟合曲线(N=44)Fig.8 Node degree distribution fitting curve of yiqi(N=44)

4.3 网络模型仿真比较

为了验证本文构建的供应链网络模型的合理性， 现运用一汽1993年～2015年供应链的实际数据， 设置仿真模型的参数， 将仿真生成的网络的度分布与一汽实际网络的度分布进行对比.

在1993年， 一汽供应链网络共有18个企业， 故设置m0=18； 统计1993年～2015年间， 一汽供应链网络内企业的进入与退出行为， 设置m=2,n=1,r=1； 在2015年， 一汽供应链网络成员发展到44个企业， 故N=44， 即网络从18个初始节点开始演化， 待网络内的节点数量N=44时停止演化.

对仿真生成的网络进行度分布的幂率拟合， 如图 9 所示， 其中幂率指数为2.526， 可决系数R-square为0.980 8， 说明拟合效果较好.

图 9 仿真网络节点度分布拟合曲线(N=44)Fig.9 Node degree distribution fitting curve of the simulation network(N=44)

对比图 8 和图 9， 仿真生成的网络比一汽实际网络的幂率指数大， 但是都在1～3之间， 仍然符合幂率分布， 具有无标度的特性. 同时， 仿真生成的网络中， 节点中最大的度值为14， 其余节点的度值大都分布在1～4间， 而一汽网络中最大的度值为16， 节点度值也大多分布在1～4间， 说明仿真生成的网络与一汽实际网络之间的差异性不大， 进而验证了本文构建的复杂网络模型的合理性和适用性.

5 结 论

本文将供应链网络视为由众多厂商成员， 根据彼此间的经济合作与竞争关系， 在空间网络上形成的复杂网络. 引入反择优断开规则， 从厂商节点进入、 退出和合作机制3方面对供应链网络进行模型的构建. 在演化模型的基础上， 从仿真模拟和实证分析两方面对供应链网络进行分析. ① 运用MATLAB模拟供应链网络的生成过程， 并从统计特征方面研究网络的统计规律和演化特征， 结果证明供应链网络的无标度性. ② 根据一汽实际网络的数据设置仿真参数， 对比一汽实际网络和仿真生成的网络的特征， 验证了本文构造的演化模型的合理性.

本文在构造供应链网络模型时， 假设所有厂商节点的择优连接依据度值的大小来选择， 没有考虑度值测度其他方面的因素， 这是本文的不足之处， 也是未来的研究方向.

参考文献：

[1] Lin F R, Shaw M J. Reengineering the order fulfillment process in supply chain networks[J]. Flexible Services and Manufacturing Journal, 1998, 10(3)： 197-229.

[2] Shi W， Wu G D. Supply chain enterprises co-evolution model from ecological perspective[J]. Advances in Information Sciences & Service Sciences, 2013, 5(9)： 69-79.

[3] Marchi J J, Erdmann R H, Rodriguez C M T, et al. Understanding supply networks from complex adaptive systems[J]. BAR-Brazilian Administration Review, 2014, 11(4)： 441-454.

[4] Kühnert C, Helbing D, West G B. Scaling laws in urban supply networks[J]. Physica A Statistical Mechanics & Its Applications, 2006, 363(1)： 96-103.

[5] 李彬, 季建华, 李国威. 综合收益和风险的供应链鲁棒性指标模型研究[J]. 上海交通大学学报, 2013, 47(3)： 484-488.

Li Bin, Ji Jianhua, Li Guowei. Study on supply Chain robustness index mode considering profits and risks[J]. Journal of Shanghai Jiaotong University, 2013, 47(3)： 484-488. (in Chinese)

[6] Outmal I, Kamrani A, Nasr E S A, et al. Modeling and performance analysis of a closed-loop supply chain using first-order hybrid Petri nets[J]. Advances in Mechanical Engineering, 2016, 8(5): 1-15.

[7] Jahani A, Murad M A A, Sulaiman M N, et al. An agent-based supplier selection framework： a case-based reasoning approach[M]. Heidelberg: Springer, 2011.

[8] Kato W, Arizono I, Takemoto Y. A proposal of bargaining solution for cooperative contract in a supply chain[J]. Journal of Intelligent Manufacturing, 2018, 29(3): 559-566.

[9] Barabási A L, Albert R, Jeong H. Mean-field theory for scale-free random networks[J]. Physica A Statistical Mechanics & Its Applications, 1999, 272(1-2)： 173-187.

[10] 曹文彬, 熊曦. 边效益因素下复杂供应链网络局域演化机制[J]. 计算机应用研究, 2016, 33(1)： 75-77.

Cao Wenbin, Xiong Xi. Local-world evolution model of complex supply chainnetwork under edge benefit[J].Application Research of Computers, 2016, 33(1)： 75-77. (in Chinese)

[11] 丁青艳. 复杂网络结构下供应链企业间合作关系研究[D]. 北京： 北京交通大学, 2012.

[12] 谢珊珊. 基于演化模型的供应链网络脆弱性研究[D]. 武汉： 华中科技大学, 2015.

[13] 孙军艳, 傅卫平, 王雯. 以制造商为核心的复杂供应链网络多级局域世界演化模型[J]. 计算机应用, 2015, 35(2)： 560-565.

Sun Junyan, Fu Weiping, Wang Wen. Evolving model of multi-local world based on supply chain network with core of manufacturers[J]. Journal of Computer Applications, 2015, 35(2)： 560-565. (in Chinese)

[14] 沈爱忠, 郭进利, 索琪, 等. 基于多层网络的供应链金融建模与分析[J]. 计算机应用研究, 2017, 34(12)： 3628-3631.

Shen Aizhong, Guo Jinli, Suo Qi, et al. Modeling and analysis of supply chain finance based on multiplex networks[J]. Application Research of Computer, 2017, 34(12)： 3628-3631. (in Chinese)

[15] Kim Y, Choi T Y, Yan T, et al. Structural investigation of supply networks： a social network analysis approach[J]. Journal of Operations Management, 2011, 29(3)： 194-211.

[16] 孙军艳, 傅卫平, 王雯. 基于复杂网络理论的B2C电商供应链网络分析[J]. 西安理工大学学报, 2015, 31(4)： 391-399.

Sun Junyan, Fu Wenping, Wang Wen. Analysis of the B2C electronic commerce supply chain network based on complex network theory[J]. Journal of Xi’an University of Technology, 2015, 31(4)： 391-399. (in Chinese)

[17] 孙军艳， 王雯， 傅卫平， 等. 轿车供应链复杂自适应系统演化规律[J]. 计算机集成制造系统， 2016, 22(8)： 2011-2022.

Sun Junyan， Wang Wen， Fu Weiping， et al. Evolution of car supply chain complex adaptive system[J]. Computer Integrated Manufacturing Systems, 2016, 22(8)： 2011-2022. (in Chinese)

[18] 李广， 赵道致. 供应链网络的无标度特性研究[J]. 工业工程， 2012, 15(1)： 28-32.

Li Guang, Zhao Daozhi. A study on the scale-free characteristics of supply chain network[J]. Industrial Engneering Journal, 2012, 15(1): 28-32. (in Chinese)

[19] Ji G， Gunasekaran A. Evolution of innovation and its strategies： from ecological niche models of supply chain clusters[J]. Journal of the Operational Research Society， 2014， 65(6)： 888-903.

[20] 刘绘珍. 基于组织进入、 退出和合作的技术创新网络演化模型[J]. 数学的实践与认识， 2016, 46(6)： 23-29.

Liu Huizhen. Base on organized into enter and exit and cooperative technology innovation networks model[J]. Mathematics in Practice and Theory， 2016, 46(6)： 23-29. (in Chinese)