不同抽样估计方法在全国各省水产品产量上的应用

裴 玲

(西北师范大学，甘肃 兰州 730070)

1 前言

近些年来随着社会主义经济的蓬勃发展，水产品的产量以及地区的分布不再仅仅局限于江南地区，更多的像北方的一些内陆城市采取池塘养殖的方法来就近获得新鲜的水产品。根据本文搜集的数据显示，当前中国对水产品的需求量不小，不论是高级餐厅还是小家饭馆，都呈现出了一种供不应求的状态，可见应重视对该领域的研究。本文就在于观察到这一经济现象，所以采取较为合理的抽样估计办法对2015年各省市的水产品产量均值进行简单估计。这在一定程度上不仅仅是研究全国各省市水产品产量的状况，更是为研究这一领域提供一个较为适合的办法。抽样估计方法多种多样，选择一个良好的估计方法就意味着这一领域的研究精度在一定程度上得到了提高。

2 研究方法和数据说明

2.1 研究方法

本文主要研究的内容是在Excel软件的基础上，应用经济统计的抽样调查理论方法，从横向的角度分析不同抽样估计方法在2015年全国各省水产品产量上的应用。总体抽样思路为：第一，抽样所选的抽样框为中国统计年鉴各省的排序编码，初级抽样单元为单个省；第二，考虑到数据特点，为便于说明问题，PPS抽样选择规模累积等距抽样；第三，分层抽样共分为两层：第一抽样层和第二抽样层。

2.2 数据说明

本文采用2015年全国30个省(除过西藏)的水产品产量作为主变量，水产养殖面积为辅变量进行分析。数据来源于《中国统计年鉴—2016》。

3 简单随机抽样及估计

在简单随机抽样的具体实施过程中，首先对已经选择的30个省市进行编号，以01～30为编号，编好的编码，就是所谓的抽样框，如表1。 用随机数生成器在01～30中产生9个随机数为：03、09、02、27、24、26、11、22、25即河北、上海、天津、甘肃、贵州、陕西、浙江、重庆、云南九个省被抽选为样本，抽取结果如表2所示。

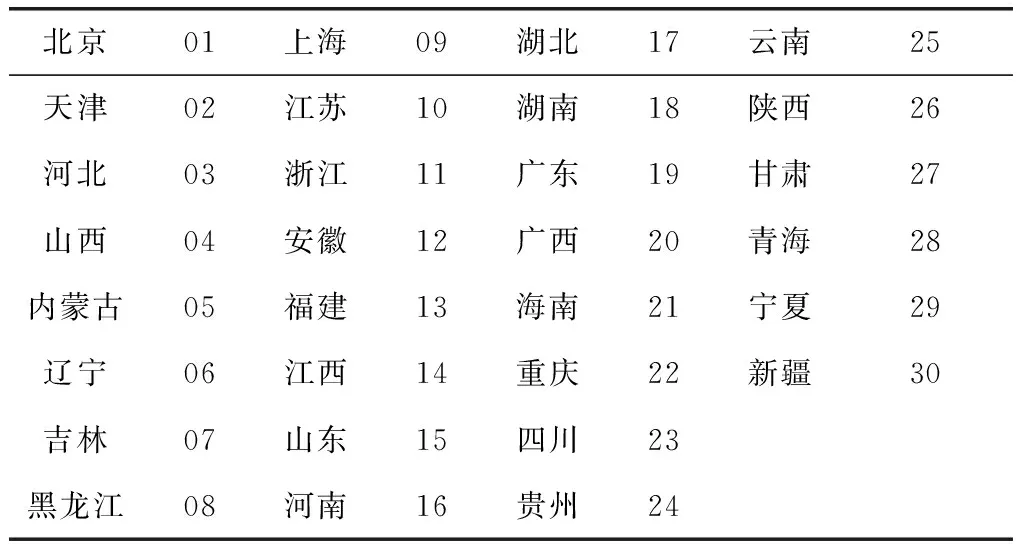
表1 所选省市简单随机抽样抽样框

表2 所选省市简单随机抽样结果

(1)总体均值估计量为：

(2)总体均值方差估计量为：

(3)以95%的置信条件可以得到总体均值的区间估计为：

106.65±1.96x52.41，即[3.93 ，209.3]

4 PPS抽样及估计

PPS估计本身就包含很多种不同类型的抽样方法，其中，规模累积等距抽样属于较为常用的方法，也是很多学者较为推崇的方法，所以在本文的写作过程中就选择规模累积等距抽样作为pps估计的主要方法。在这个选择的基础上，对全社会水产养殖面积计算累计规模、规模代码区间及规模比重，如表3所示。

从表3得知，30个省市水产品产量累积和为8465，这里抽取30%的样本，经计算选取9个样本较为合适，等距抽样的间隔为K=M0n=8465/9≈940，借助随机数生成器在1～940中产生一个随机代码，作为第一个抽样代码，抽选结果为197，相应的样本单位为陕西，经查阅对应Y值为15.52。按照规模等距抽样方法给各初始代码分别加K、2K……8K得到抽样单位的所有代码、相应的抽样单位及样本单位的Y值如表4所示。

表3 各省市全社会水产养殖面积规模及起止代码区间及规模比重

表4 抽样代码和抽样结果

经计算汉森—赫维茨总体总量估计量为：

(1)总体均值估计量为：

(2)总体均值方差估计量为：

(3)以95%的置信条件可以得到总体均值的区间估计为：

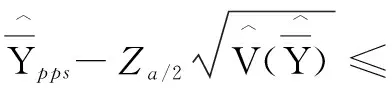
228.5±1.96x40.9，即[148.34，308.66]

5 分层抽样估计

本文为一般分层抽样，一共分为两层。为了分层抽样的实施，先对我国30个省市进行聚类分层，如表5。

表5 各省市分层表

由表5可知，第一层为规模明显较大的层，因此该层为第一抽样调查层；第二层为剩余省份组成的层，因此该层为第二抽样调查层。一共抽取9个样本，即n=9。为了估计的准确度，这里采用耐曼分配方法确定各层的样本个数ni。

表6 关于样本量分配的计算

由表6中的数据可得耐曼分配如下：

用随机数生成器在第一层的编码中产生4个随机数为：15、11、13、06，即山东、浙江、福建、辽宁四个省被抽选为样本；第二层的编码中产生5个随机数为：16、23、22、25、08，即河南、四川、重庆、云南、黑龙江五个省被抽选为样本，抽取结果如表7所示。

(1)总体均值估计量为：

(2)总体均值方差估计量为：

(3)以95%的置信条件可以得到总体均值的区间估计为：

224.29±1.96x16.2，即[192.54，256.04]

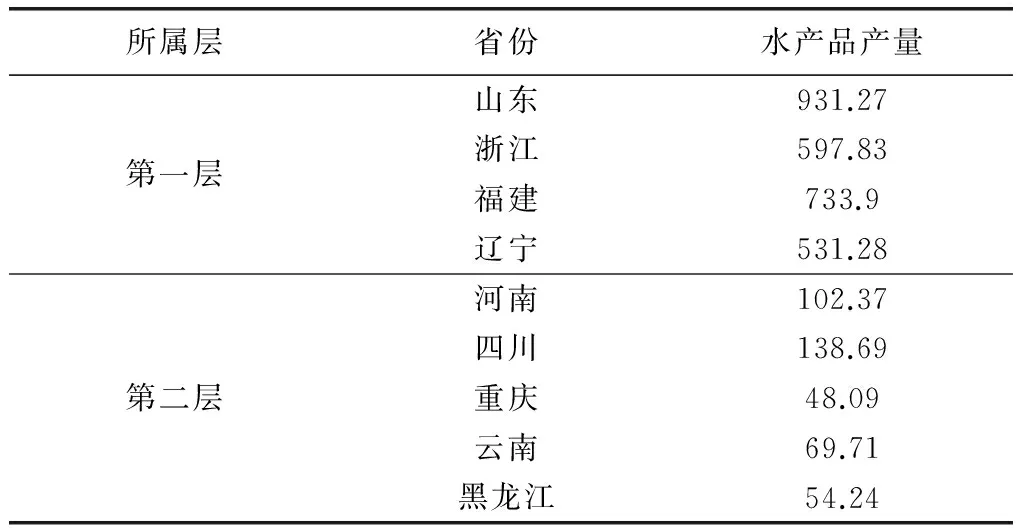
表7 中国30个分层抽样结果

表8 关于样本统计量的计算

6 结论

(1)首先对简单随机抽样、PPS抽样简单比较，可以看出在均值估计中，PPS估计的效果明显优于简单随机抽样。具体来讲，PPS抽样均值的估计值为228.5和真实值仅仅相差6.1，均值抽样方差为1676.4；而简单随机抽样均值为106.65与真实值相差115.75，抽样方差达到2474。因此，在简单随机抽样和分层抽样计算结果的基础上，PPS估计的效率要高于简单随机抽样。在实际调研分析过程中，根据自身需要和限制，选用抽样效率相对较高的办法。

(2)在利用分层抽样的方法进行估计时，可以明显看到，均值估计精度被提高了不少。均值估计量与真实值仅仅相差1.89，抽样方差也仅有262.7，相比简单随机抽样和PPS抽样降低了很多，这说明在本文中分层抽样的抽样效率高于简单随机抽样和PPS抽样。从差异的角度讲，分层抽样和PPS抽样的效率无较大的差异，在实际研究中，根据费用等限制条件综合选取最优的抽样方法。

综上所述，简单随机抽样、PPS抽样、分层抽样对于本文研究命题估计最好的为分层抽样。

[1] 倪家勋.抽样调查[M].桂林：广西师范大学出版社，2002.

[2] 陶瑞妮,张忱.PPS抽样方法在固定资产投资估计中的应用[J].现代商贸工业,2014,(9):125-126.

[3] 张玉. PPS抽样方法在我国出口贸易预测中的应用[J].经济研究导刊,2011,(2):156-157.

[4] 李睆玲，雷恒，陈伟伟. PPS 抽样方法在我国农村居民生活消费支出估计中的应用[J]. 长春金融高等专科学校学报,2009,(3):49-51.