ARIMA?SVM的物流需求预测模型
杨建成


摘 要: 物流需求是多种因素综合作用的结果,具有规律性和特殊性,变分十分复杂,导致当前物流需求预测模型的预测效果差,难以满足物流管理的实际应用要求。为了解决物流需求建模过程中存在的难题,提出基于ARIMA?SVM的物流需求预测模型。首先对当前物流需求预测的研究现状进行分析,找到引起物流需求预测效果的原因;然后选择差分自回归滑动平均模型对物流需求的规律性变化特点进行建模,支持向量机对物流需求的特殊性变化特点进行建模;最后采用权值方式确定物流需求预测的预测结果,并采用物流需求的预测实例分析模型的有效性。结果表明,ARIMA?SVM的物流需求预测结果要优于当前其他物流需求预测模型,为其他预测问题提供了一种建模工具。
关键词: 物流管理; 随机性变化特点; ARIMA?SVM; 权值的确定; 预测模型; 支持向量机
中图分类号: TN911.1?34; TP391 文献标识码: A 文章编号: 1004?373X(2018)09?0182?05
Abstract: The logistics demand affected by many factors has the characteristics of regularity, particularity and complex variation, which leads to the poor prediction effect of current logistics demand forecasting model, and is difficult to meet the practical application requirements of logistics management. In order to solve the problems existing in logistics demand modeling process, a logistics demand prediction model based on ARIMA?SVM is proposed. The research status of the current logistics demand forecasting is analyzed to find out the reason influencing the logistics demand forecasting results. The autoregressive integrated moving average (ARIMA) model is selected to model the regular variation characteristics of logistics demand. The support vector machine (SVM) is used to model the special variation characteristics of logistics demand. The weight is used to determine the prediction results of the logistics demand forecasting. The validity of the logistics demand forecasting model is analyzed by means of an example. The results show that the result of logistics demand forecasting model based on ARIMA?SVM is better than that of other logistics demand forecasting models, which provides a modeling tool for other forecasting problems.
Keywords: logistics management; stochastic variation characteristic; ARIMA?SVM; weight determination; prediction model; support vector machine
0 引 言
随着经济全球化进展的不断加速,物流行业得到了前所未有的发展,而物流园区规划是物流业发展的基础[1]。物流需求的建模与预测是合理规划物流园区的前提条件。物流需求的建模与预测是指对某区域的物流历史数据和资料进行收集和分析,对将来物流需求进行估计,以描述物流需求将来的变化趋势[2]。物流需求的建模与预测涉及多个方面的技术,如计算机技术、信息处理技术、数量统计技术等,因此物流需求的建模与预测面临着巨大的挑战[3?5]。
当前物流需求的建模和预测方法很多,可以将物流需求预测的研究划分为2个阶段:传统阶段和现代阶段[6],传统阶段的物流需求模型主要有:增长率法、指数平滑法、线性回归法、差分自回归移动平均法等,其中增长率法、指数平滑法和差分自回归移动平均法属于时间序列建模方法,增长率法、指数平滑法要求物流需求是一种增长的变化态势,这对于长期物流需求进行预测是可以的,但对于短期物流需求预测的建模就不一定可行,因为短期物流需求不一定完全呈增长变化态势,有可能还有下降的变化态势,因此它们的限制性十分明显[7]。差分自回归移动平均法十分灵活,而且通用性强,成为最常用的一种物流需求预测建模方法,但其是一种线性建模方法,无法对物流需求的其他变化特点进行预测,因此预测效果有待改善[8?9]。现代阶段的物流需求模型主要有:灰色模型、神经网络、支持向量机等[10?12],它们属于非线性建模方法,主要描述物流需求与影响因素之间的非线性映射关系,物流需求的预测效果要明显优于传统模型。物流需求与一个区域经济、交通、政策等因素密切相关,不仅具有一般经济问题的周期性变化特点,同时还具有随机性变化特点。单一模型只能对物流需求的单一特点进行建模,导致物流需求预测效果差。为此,有学者提出物流需求的组合预测模型,如灰色神经网络模型,该模型将灰色模型和BP神经网络组合在一起,通过它们对物流需求的变化特点进行建模,获得了较高的预测精度。然而BP神经网络自身存在一定的不足,影响了物流需求的组合预测结果,因此组合型中的单一模型选择十分关键,成为影响物流需求预测精度的重要技术之一。
为了解决物流需求建模过程中存在的难题,提出基于ARIMA?SVM的物流需求预测模型。首先选择差分自回归滑动平均模型对物流需求的规律性变化特点进行建模,支持向量机对物流需求的特殊性变化特点进行建模,然后采用权值方式确定物流需求预测的预测结果,最后采用物流需求预测的实例分析模型的有效性。结果表明,ARIMA?SVM的物流需求预测结果要优于当前其他物流需求预测模型,为其他预测问题提供了一种建模工具。
1 相关理论
1.1 差分自回归滑动平均模型
差分自回归滑动平均模型是一种经典的时间序列数据分析方法,根据问题的历史数据挖掘各种因素对问题结果的影响,揭示时间序列的变化特点。差分自回归滑动平均模型首先假设时间序列能够由一些滞后序列进行描述,即AR模型;然后假设其可以由若干白噪声序列刻画,即MA模型,它们组成在一起就形成了ARIMA模型。
对于物流需求量的数据,通过差分变换对其进行处理,得到平稳的数据[Yt],具体形式为:

ARIMA模型的工作步骤如下:

1) 收集数据,并进行相应的预处理。对本文的研究来说,收集物流需求的历史数据,对其变化特点进行观察和检验,如果该数据为非平稳时间序列,那么就将其变为平稳时间序列,如果该数据为非正态分布,经过一定的变化成为正态分布的数据。
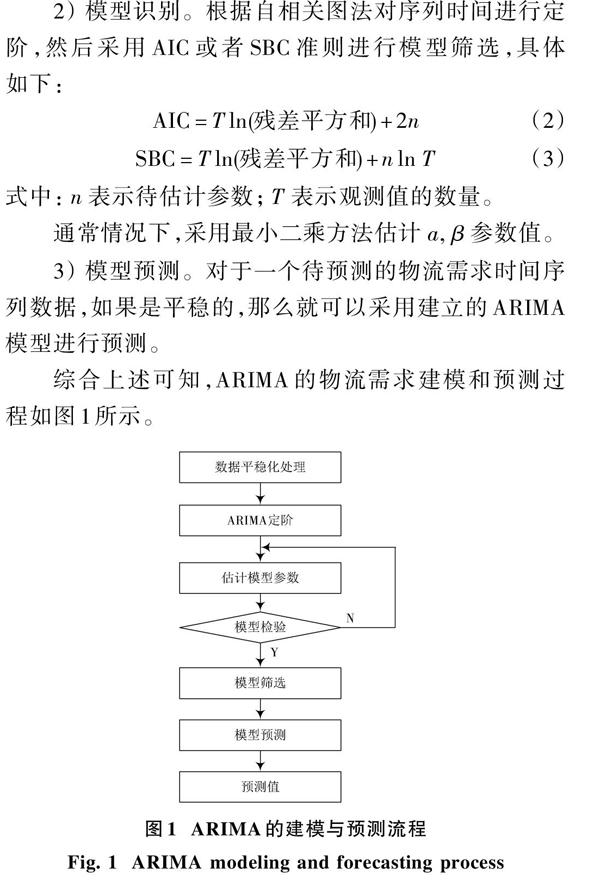
2) 模型识别。根据自相关图法对序列时间进行定阶,然后采用AIC或者SBC准则进行模型筛选,具体如下:
3) 模型预测。对于一个待预测的物流需求时间序列数据,如果是平稳的,那么就可以采用建立的ARIMA模型进行预测。
综合上述可知,ARIMA的物流需求建模和预测过程如图1所示。

2 ARIMA?SVM的物流需求预测模型
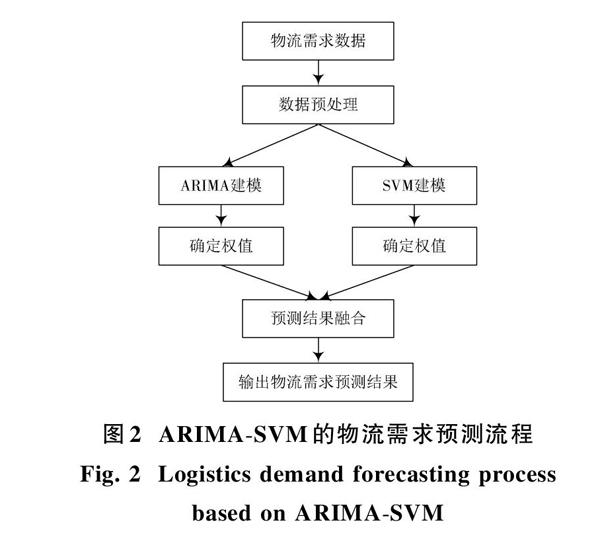
物流需求与因素相关,不仅具有周期性、线性等变化特点,同时具有随机性、时变性、非线性等变化特点,单一模型无法描述物流需求的变化特点,导致预测精度低,结果不稳定,由于ARIMA模型可以对物流需求的周期性、线性等变化特点进行建模,而SVM模型可以对物流需求的随机性、时变性、非线性等变化特点进行建模,ARIMA?SVM模型充分利用ARIMA和SVM的优点,有效解决了ARIMA和SVM的缺陷,改善了物流需求的预测效果,具体流程如图2所示。
3 物流需求预测的实例分析
3.1 物流数据及相关设置
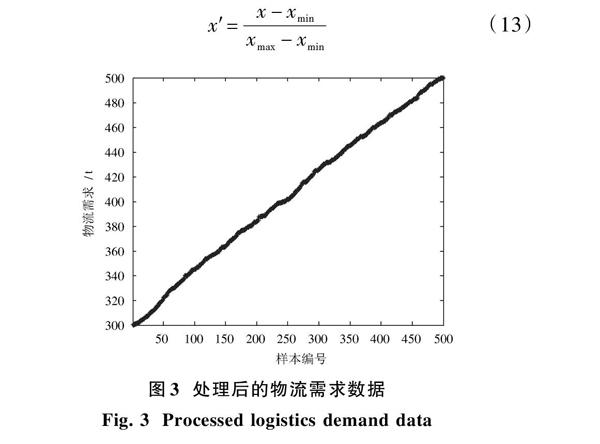
为了测试ARIMA?SVM的物流需求建模与预测性能,采用一个地区的物流需求数据作为研究对象,数据如图3所示。首先采用式(13)对原始物流需求数据进行处理,以减少数据幅度变化太大带来的不利影响。
3.2 ARIMA的物流需求预测结果分析
通过DSP软件对物流需求数据进行处理,确定它们分别表示回归和移动平均的阶数[p]和[q,]得到最优的[p=5,][q=2。]根据[p=5]和[q=2]建立基于ARIMA的物流需求预测模型,并对最后200个数据进行预测,得到的物流需求预测结果如图4所示。对图4的物流需求預测结果进行分析可以发现,ARIMA模型只能对物流需求的总体变化趋势进行拟合,但是无法对物流需求预测的细节变化特点进行描述,如随机性等,导致物流需求预测的误差比较大,物流需求预测效果有待改善。
3.3 SVM的物流需求预测结果分析

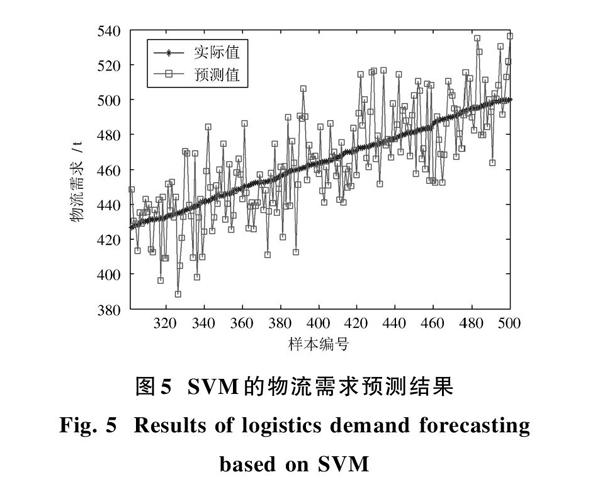
采用Matlab 2015实现支持向量机算法,并通过留一法确定支持向量机的参数[C=100.78,σ=8.78。]根据参数[C=100.78,][σ]=8.78建立基于SVM的物流需求预测模型,并对最后200个数据进行预测,得到的物流需求预测结果如图5所示。对图5的物流需求预测结果进行分析可知,SVM的物流需求效果要明显优于ARIMA模型,提高了物流需求预测精度,而且物流需求的预测误差明显减少,但是物流需求预测的预测结果还有待进一步改善。
3.4 ARIMA?SVM的物流需求预测结果分析
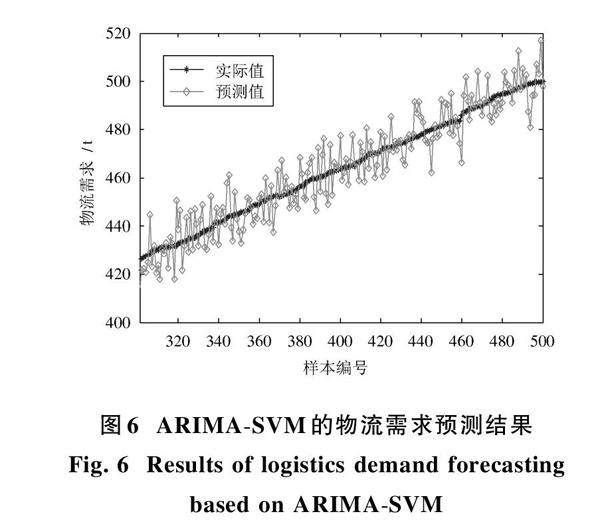
将ARIMA的物流需求预测结果和SVM的物流需求预测结果作为输入,物流需求的期望值作为输出,采用SVM进行学习,确定ARIMA和SVM的物流需求预测结果权值,最后通过权值计算物流需求的预测结果,结果如图6所示。通过图6可知,ARIMA?SVM的物流需求预测结果要优于单一ARIMA和SVM的物流需求预测结果,这是因为其综合利用了ARIMA和SVM的优点,解决了它们存在的局限性,提高了物流需求预测精度,实验结果表明了ARIMA?SVM的优越性。
4 结 论
物流需求预测是物流管理领域中的一个重要研究内容,为了改善物流需求的预测效果,设计了基于ARIMA?SVM的物流需求预测模型,并进行物流需求预测的具体应用实例分析,根据实例分析结果可以得到如下结论:
1) 物流需求与一个地方所处的位置、经济、交通、地方政府支持等因素相关,具有其他经济问题的一般规律,如周期性、线性等,同时具有自身的特殊变化特点,如随机性、时变性、非线性等,导致单一模型的物流需求预测精度低,预测结果不稳定。
2) ARIMA模型可以对物流需求的一般变化规律进行建模,而SVM模型可以对物流需求的特殊变化特点进行建模,ARIMA?SVM模型充分利用了ARIMA和SVM的优点,能够有效克服单一ARIMA和SVM的缺陷,有效提升了物流需求的预测精度,而且物流需求的预测结果更加稳定、可靠,具有较明显的优势。
3) ARIMA和SVM的组合方式有多种形式,其中权值组合的ARIMA?SVM的预测结果相对更优,实际应用价值更高,同时也为其他预测问题提供了一种有效的建模和预测工具。
参考文献
[1] 赵秋红,汪寿阳,黎建强.物流管理中的优化方法与应用分析[M].北京:科学出版社,2006.
ZHAO Qiuhong, WANG Shouyang, LI Jianqiang. Optimization methods and application analysis of logistics management [M]. Beijing: Science Press, 2006.
[2] 孙建丰,向小东.基于灰色线性回归组合模型的物流需求预测研究[J].工业技术经济,2007(10):146?148.
SUN Jianfeng, XIANG Xiaodong. Research on logistics demand prediction based on grey linear regression combination model [J]. Industrial technology and economy, 2007(10): 146?148.
[3] 王晓原,李军.灰色GM(1,1)模型在区域物流规模预测中的应用[J].武汉理工大学学报(交通科学与工程版),2005(3):415?417.
WANG Xiaoyuan, LI Jun. The application of grey GM(1, 1) model in the prediction of regional logistics scale [J]. Journal of Wuhan University of Technology (transportation science and engineering), 2005(3): 415?417.
[4] 陈森,周峰.基于灰色系统理论的物流需求预测模型[J].统计与决策,2006(3):59?60.
CHEN Sen, ZHOU Feng. Logistics demand forecasting model based on grey system theory [J]. Statistics and decision, 2006(3): 59?60.
[5] 魏连雨,庞明宝.基于神经网络的物流量预测[J].长安大学学报(自然科学版),2004,24(6):55?59.
WEI Lianyu, PANG Mingbao. Prediction of material flow based on neural network [J]. Journal of Changan University (natural science edition), 2004, 24(6): 55?59.
[6] 尹艳玲.基于自适应神经网络的物流需求预测研究[J].河南理工大学学报(自然科学版),2010,29(5):700?704.
YIN Yanling. Research on logistics demand prediction based on adaptive neural network [J]. Journal of Henan Polytechnic University (natural science edition), 2010, 29(5): 700?704
[7] 后锐,张毕西.基于MLP神经网络的区域物流需求预测方法及其应用[J].系统工程理论与实践,2005,22(12):43?47.
HOU Rui, ZHANG Bixi. The prediction method of regional logistics demand based on MLP neural network and its application [J]. System engineering theory and practice, 2005, 22(12): 43?47.
[8] 唐伟鸿,李文锋.基于时间序列的支持向量机在物流预测中的应用[J].物流科技,2005(1):8?11.
TANG Weihong, LI Wenfeng. Application of time series based support vector machines in logistics forecasting [J]. Logistics science, 2005(1): 8?11.
[9] 胡燕祝,吕宏义.基于支持向量回归机的物流需求预测模型研究[J].物流技术,2008,27(5):66?68.
HU Yanzhu, L? Hongyi. Research on logistics demand forecasting model based on support vector regression machine research [J]. Logistics technology, 2008, 27(5): 66?68
[10] 耿立艳,赵鹏,张占福.基于二阶振荡微粒群最小二乘支持向量机的物流需求预测[J].计算机应用研究,2012,29(7):2558?2560.
GENG Liyan, ZHAO Peng, ZHANG Zhanfu. Logistics demand prediction based on two order oscillating particle swarm least squares support vector machine [J]. Computer application research, 2012, 29(7): 2558?2560.
[11] 初良勇,田质广,谢新连.组合预测模型在物流需求预测中的应用[J].大连海事大学学报,2004,30(4):43?46.
CHU Liangyong, TIAN Zhiguang, XIE Xinlian. Application of combination forecasting model in the logistics demand forecasting [J]. Journal of Dalian Maritime University, 2004, 30(4): 43?46.
[12] 闫莉,薛惠峰,陈青.基于灰色马尔可夫模型的区域物流规模预测[J].西安工业大学学报,2009,29(5):495?497.
YAN Li, XUE Huifeng, CHEN Qing. Prediction of the scale of regional logistics based on Grey Markov model [J]. Journal of Xian Technological University, 2009, 29(5): 495?497.

