三轴磁传感器的校正方法

刘建敬 陈丽 汪冬瑾 戚红向

摘 要： 为了消除三轴磁传感器自身的误差，针对其存在的偏移误差、灵敏度误差和非正交误差的特点，建立三轴磁传感器的误差校正模型，利用批量最小二乘拟合方法提出相应的磁传感器校正方法，不需要额外的加速计辅助即可对三轴磁传感器进行校正，并通过磁传感器的误差校正实验进行验证。校正实验结果表明，该三轴磁传感器校正后的均方根误差减小到103 nT，磁传感器的校正方法可以有效消除自身的误差，并且不需要其他辅助手段。

关键词： 磁传感器; 误差校正模型; 最小二乘; 拟合方法; 地磁场; 均方根误差

中图分类号： TN03?34; TJ413.6 文献标识码： A 文章编号： 1004?373X（2018）09?0179?03

Abstract： In order to eliminate the errors of 3?axis magnetic sensor itself， an error correction model of 3?axis magnetic sensor was established according to the characteristics of the offset error， sensitivity error and non?orthogonal error. On the basis of the batch least square fitting method， the corresponding correction method of magnetic sensor is proposed， which can correct the errors of magnetic sensor without the additional accelerometer. The calibration method of 3?axis magnetic sensor was verified with experiment. The results show that the root?mean?square error corrected with 3?axis magnetic sensor is decreased to 103 nT， and the correction method of magnetic sensor can eliminate the errors itself without other auxiliary means.

Keywords： magnetic sensor; error correction model; least square; fitting method; geomagnetic field; root?mean?square error

0 引 言

地磁场是天然存在的物理参考场，为载体的导航和姿态检测技术提供了很好的参考基准，因此，基于地磁场的导航和姿态检测技术日益得到关注和研究[1?3]。磁传感器是测量弱磁场的敏感元件，具有体积小、响应快、成本低、抗高过载等优点，被广泛应用于地磁导航领域[4]。

不过，由于制作工艺水平的限制，磁传感器自身不可避免地存在误差，主要有偏移误差、灵敏度误差和非正交误差等。偏移误差是由传感器和电路的电气参数不对称造成零位偏移而引起的误差;灵敏度误差是由每个通道的传感器灵敏度和电路增益不一致而引起的误差;非正交误差是由传感器的三个测量方向不完全垂直而引起的误差[5?6]。

对于组合的三轴磁传感器（如霍尼韦尔公司的HMC1021和HMC1022），垂直安装的敏感轴很难保持其与安装平面的垂直关系。如果假设垂直轴为理想轴，建立三轴磁传感器的误差模型，并且引入加速计辅助可以进行校正，但是传感器安装难度较大，并且三轴加速度计自身存在与三轴磁传感器类似的问题，因此校正方法过于复杂[7?8]。

针对三轴磁传感器存在的偏移误差、灵敏度误差和非正交误差[9?10]，以水平面内的敏感轴为理想轴建立了三轴磁传感器的误差校正模型，并提出磁传感器的校正方法，无需加速度计辅助即可对三轴磁传感器的误差进行校正，实现地磁场矢量的准确测量。

1 磁传感器误差校正模型

假设三轴磁传感器的两个测量方向（X轴和Y轴）所在平面与磁传感器的底面平行，并且其中一个测量方向（X轴）与理想测量方向一致。如图1所示，[OXYZ]为磁传感器的理想坐标系（正交坐标系），三个坐标轴方向为磁传感器的理想测量方向;[OXmYmZm]为磁传感器的实际坐标系（非正交坐标系），三个坐标轴方向为磁传感器的实际测量方向;坐标系原点[O]为磁传感器的中心，[OXY]与[OXmYm]位于同一平面内且平行于底面，[OX]与[OXm]重合。[η1，][η2]和[η3]为地磁传感器的三个非正交误差角，其中[η1]为[OY]与[OYm]的夹角，[η2]为[OZm]在[OXZ]面的投影与[OZ]的夹角，[η3]为[OZm]与投影的夹角。

2 磁传感器校正方法

地磁场是稳定的均匀磁场，在某点附近可以认为地磁场矢量是恒定不变的，即如果地磁场强度为[H，]那么[HTH=H]。结合式（4）可知：

3 磁传感器校正实验

將磁传感器放置在一个纯净的地磁场环境中，并安装在无磁转台上，然后绕4个不同方向对磁传感器进行旋转，并将磁传感器的测量数据实时发送到PC上位机，对接收数据按照第2节中的方法进行处理，计算磁传感器的9个误差系数，其中3个灵敏度误差系数分别为1.019，1.062和0.955，偏移误差系数分别为-80.1 mV，69.2 mV和48.9 mV，3个非正交误差角的角度值分别为0.53°，0.99°和0.80°。

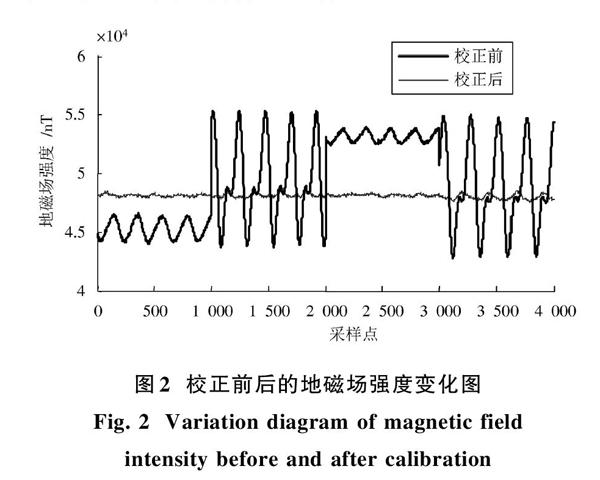
利用计算得到磁传感器误差系数，根据式（3）对磁传感器的测量数据进行误差校正，校正前后磁传感器测量的地磁场强度变化如图2所示。由图2可以看到，在校正之前，由于存在较大的误差，测量的地磁场强度波动非常大，而校正之后，地磁场强度大幅地减小，基本变成一条直线，与实际情况一致。通过对磁传感器进行校正，其地磁场强度的均方根误差由校正前的3 787 nT减小到校正后的103 nT。由此表明，磁传感器的校正方法能够有效减小其自身存在的各种误差。

4 结 论

为了消除三轴磁传感器自身存在的各种误差的影响，对其自身误差分为灵敏度误差、偏移误差和非正交误差。结合这三种误差的表现形式，建立三轴磁传感器的校正模型，并且利用地磁场的恒定不变特性，提出了利用批量最小二乘拟合方法的校正方法，计算磁传感器误差校正模型中的9个误差系数，从而实现对三轴磁传感器的校正。然后，进行三轴磁传感器的校正实验，实验结果表明，磁传感器校正后的均方根误差由3 787 nT减小到103 nT。因此，该校正方法能够有效消除磁传感器自身存在的误差，并且无需外部辅助。

参考文献

[1] 李兴城，张慧心，张双彪.地磁导航技术的发展现状[J].飞航导弹，2013（10）：80?83.

LI Xingcheng， ZHANG Huixin， ZHANG Shuangbiao. Development of geomagnetic navigation technology [J]. Winged missiles journal， 2013（10）： 80?83.

[2] 陈卓，田风勋，孙建军.地磁导航关键技术研究发展综述[J].测绘与空间地理信息，2016，39（1）：16?18.

CHEN Zhuo， TIAN Fengxun， SUN Jianjun. Summarization of studying on geomagnetic navigation key technique [J]. Geomatic & spatial information technology， 2016， 39（1）： 16?18.

[3] 赵国荣，黄婧丽，胡正高.地磁辅助惯性组合导航技术分析[J].系统仿真技术，2013，9（2）：119?123.

ZHAO Guorong， HUANG Jingli， HU Zhenggao. Geomagnetic aided inertial navigation technical analysis [J]. System simulation technology， 2013， 9（2）： 119?123.

[4] 艾文娟，刘岩.基于MEMS技术的惯性/地磁组合导航[J].自动化与仪器仪表，2016（1）：110?113.

AI Wenjuan， LIU Yan. Inertial/geomagnetic integrated navigation based on MEMS technology [J]. Automation & instrumentation， 2016（1）： 110?113.

[5] 杨宇彬，汤国建，包为民.地磁姿态探测器的实时标定方法研究[J].飞行力学，2014，32（1）：93?96.

YANG Yubin， TANG Jianguo， BAO Weimin. Real?time calibration method of magnetometer [J]. Flight dynamics， 2014， 32（1）： 93?96.

[6] 张娇，陈静，杨栓虎.三轴磁阻式传感器标定方法研究[J].弹箭与制导学报，2010，30（6）：46?48.

ZHANG Jiao， CHEN Jing， YANG Shuanhu. The study of calibration method of magnetic resistance sensor [J]. Journal of projectiles， rockets， missile and guidance， 2010， 30（6）： 46?48.

[7] V?EL?K J， RIPKA P， KUB?K J， et al. AMR navigation systems and methods of their calibration [J]. Sensors and actuators A： physical， 2005， 123： 122?128.

[8] V?EL?K J， RIPKA P， PLATIL A， et al. Errors of AMR compass and methods of their compensation [J]. Sensors and actuators A： physical， 2006， 129： 53?57.

[9] 付士民，孙立凯，于建楠，等.高精度磁罗经传感器设计[J].传感器与微系统，2016，35（1）：104?106.

FU Shimin， SUN Likai， YU Jiannan， et al. Design of high precision magnetic compass sensor [J]. Transducer and microsystem technologies， 2016， 35（1）： 104?106.

[10] FOSTER C， ELKAIM G. Extension of a two?step calibration methodology to include nonorthogonal sensor axes [J]. Aerospace and electronic systems， 2008， 44（3）： 1070?1078.

[11] MUNSCHY M， FLEURY S. Scalar， vector， tensor magnetic anomalies： measurement or computation [J]. Geophysical prospecting， 2011， 59（6）： 1035?1045.