基于HHT和概率神经网络的变压器局部放电故障识别

公茂法 魏景禹 姜文 接怡冰 公政 王万乐

摘 要： 为解决传统傅里叶变换和小波分解对变压器局部放电信号非平稳性的分析缺陷，以及BP神经网络易陷入局部极小点等问题，提出一种基于希尔伯特能量聚类和概率神经网络的变压器局部放电识别算法。算法利用希尔伯特?黄变换提取局部放电信号的希尔伯特能量谱，然后进行指数族聚类计算获得特征值，最后利用概率神经网络进行分类识别。分别对油中悬浮放电、沿面放电等放电类型进行模拟实验，并用此算法进行分析，实验结果表明，该算法所提取的特征值有较高的可分性，且分类识别率高，可以有效地识别变压器局部放电故障类型。

关键词： 希尔伯特?黄变换; 概率神经网络; 指数聚类; 模态分解; 局部放电; 变压器

中图分类号： TN711?34; TM85 文献标识码： A 文章编号： 1004?373X（2018）09?0152?05

Abstract： Since the traditional Fourier transform and wavelet decomposition have the defect for the non?stationary analysis of transformer partial discharge （PD） signal， and the BP neural network is easily to fall into the local minimum， a transformer partial discharge identification algorithm based on Hilbert energy clustering and probabilistic neural network （PNN） is proposed. The Hilbert?Huang transform （HHT） is used to extract the Hilbert energy spectrum of PD signals， and then the exponential family calculation is performed to obtain the feature values. The PNN is used to classify and identify the feature values. The simulation experiment was carried out for the discharge types of suspended discharge and surface discharge in oil， which are analyzed with the proposed algorithm. The experimental results show that the feature values extracted by this algorithm has high separability， and the algorithm has high classification identification efficiency， and can identify the fault types of transformer PD effectively.

Keywords： Hilbert?Huang transform; probabilistic neural network; exponential clustering; mode decomposition; partial discharge; transformer

0 引 言

局部放电故障类型是评估高压电力设备绝缘状态的重要技术指标之一，不仅反映绝缘状态水平，还可估算电力设备绝缘的使用寿命。因此对变压器局部放电故障识别算法的研究显得尤为重要。近年来，对放电信号的处理分析大多由傅里叶变换转换为能够进行时频局域化分析的小波变换，这两种方法对平稳信号都有良好的处理效果，但是，这些算法不能随信号本身时间和频率的变化由自身做出调整，不能客观反映出真实的信号特性[1]。文献[2]在列车轴承机械故障诊断中应用希尔波特?黄变换（Hilbert?Huang Transform，HHT）中的EEMD方法，取得了良好的效果。HHT是一种适用于非线性和非平稳信号的处理方法，提高了分解时对时频的适应能力。

同时，人工神经网络在模式识别技术中得到了越来越多的应用。文献[3?4]阐明了人工神经网络在模式识别上的重要地位，并应用于放电识别。文献[5?6]分别用BP神经网络和支持向量机对局部放电模式进行识别，效果良好。但在研究中发现，BP神经网络存在收敛速度慢、易陷入局部极小点等问题难以避免，同时支持向量机并不适合用于大样本多分类的问题。随着神经网络的发展，提出概率神经网络（Probabilistic Neural Network，PNN）。文献[7]利用概率神经网络的非线性映射分类能力实现逆变器的故障诊断，表现出PNN在模式识别中稳定性高、抗噪声能力强、诊断速度快和正确率高的优势。

针对以上问题，本文基于HHT和概率神经网络，提出一种希尔伯特能量聚类与概率神经网络相结合的变压器局部放电故障识别算法。该算法可以较好地避免特征提取过程中能量的损失，提高特征值的分辨性，同时计算速度快，不需要识别网络的优化，提高了局部放电识别的速度和精度。

1 局部放电信号分析和希尔伯特?黄变换

变压器中的局部放电脉冲均存在振荡分量，且大部分放电持续时间在100～300 ns，不同的放电类型其脉冲持续时间、波形的上升和下降沿所用时间，以及波形振动分量等诸多特性存在差异，为放电脉冲类型的识别提供了依据。但是实际测得的波形中存在诸多干扰分量，且为非线性、非平稳信号，本文采用HHT对原始信号进行处理。

在HHT中，瞬时频率是非常重要的概念，与传统的频率不同，瞬时频率表征信号在局部时间点上瞬态频率特性，整个持续期上的瞬时频率反映了信号频率的时变规律，据此可以对信号特征值进行提取。

对信号的时间序列[Xt]进行Hilbert变换，可得：

然而，单纯的Hilbert变换会滤掉信号中的谐波，造成信号失真，因此结合经验模态分解（Empirical Mode Decomposition，EMD）可以从原始信号中筛选出固有模态（Intrinsic Mode Function，IMF）。将满足条件的IMF分量通过多次筛选后获得，即EMD，具体方法可参考文献[8?9]。每个IMF分量的频率和尺度随信号的变化而改变，对油中悬浮放电信号进行EMD的结果如图1所示，其中imf1～imf8为IMF分量，[r]为残留余项。

在此，由于余项[rn（t）]的能量很小，只是单调函数或常量，一般不予考虑。

由HHT变换得来的放电信号可以进一步表示为幅值、频率和时间的函数，即Hilbert谱[10][H（w，t）]。

2 基于概率神经网络的模式识别

概率神经网络是一种被概率统计学普遍认可的决策策略，其理论依据是贝叶斯最小风险准则，适合模式分类。其基于非线性算子模式后验概率输出和用Parzen窗的概率密度函数估计的方法，使得PNN网络结构简单、训练简洁，且收敛速度很快，有理想的分类能力[11]。PNN结构由其原理决定，包括输入层、模式层、求和层和竞争层。

PNN网络的具体设计根据处理问题的具体情况确定。将原始数据进行归一化处理后，形成输入特征矩阵[Xmn，]其中，[m]为特征值维数，对应输入层有[m]个神经元，[n]为输入样本个数。

模式层的核心是基于欧氏距离下的高斯核函数，将输入特征样本与训练样本的距离通过高斯核函数的径向基非线性映射后得到输出向量，是实现PNN中非线性算法高精度特性的一个重要步骤，表达式如下：

模式层完成的是计算输入特征矩阵与各个模式的匹配关系，按照固定的函数进行输出。

求和层即对模式层输出的同一类别的样本进行概率归总，因此，求和层神经元数目对应训练样本故障类别[k，]每个类别汇总采用Parzen窗的概率密度函数：

竞争层的神经元个数[l]取决于输出分类的种类或组合。竞争层将求和层得出的最大后验概率密度的一组种类作为网络的最终输出。

3 仿真实验

3.1 信号分析和算法提出

变压器局部放电原因比较多，放电类型也多种多样，本文在实验室条件下搭建变压器放电模型构造4种局部放电模型：油中悬浮放电、油中沿面放电、油中气隙放电和空气中针板放电，分别对应图2a）～图2d）。模拟实验共提取样本数据40组，其中30组作为训练样本，10组为测试样本。

首先，对4种放电信号进行HHT后，得到信号对应于幅值和时频的Hilbert谱，再将Hilbert谱汇总为边际谱，如图3a）～图3d）所示分别为4种变压器局部放电的边际谱和局部放大的边际谱。由图3可以看出，不同的放电类型放电波形的频率有较大差异，且幅值主要集中分布在低频端，能量集中，在放大的局部图谱中可以看出在不同频率的含量上有着明显的差异，因此对时频谱按指数进行数据聚类，同时结合希尔伯特能量谱，实现对Hilbert谱按指数分布族提取能量特征值。

3.2 故障识别和结果分析

根据表1提取的特征值维数和数目，设置PNN网络结构为9?30?4?4。最后将用HHT變换得到的特征值送入设定好的PNN进行训练和测试，为做对比，同时将由小波变换（Wavelet Transform，WT）提取的能量特征值送入PNN进行训练和测试，实验结果如图4所示。

由图4可以看出，网络训练时，在同样分类器的条件下，经HEC算法得到的特征值使PNN对局部放电故障分类的准确率有明显提高，同时，结合图5的测试结果可以看出，在同样的网络下，识别的准确率有明显差异，表明该算法能有效提高信号特征值自身的可分性。另外，注意到由小波能量值作为特征值的测试和训练中，其误差多出现在油中悬浮放电和油中沿面放电之间，这是由于信号特征相似度高，且小波分解的尺度固定，使频率适应性不足，视频分解不精确，对特征提取产生了影响。

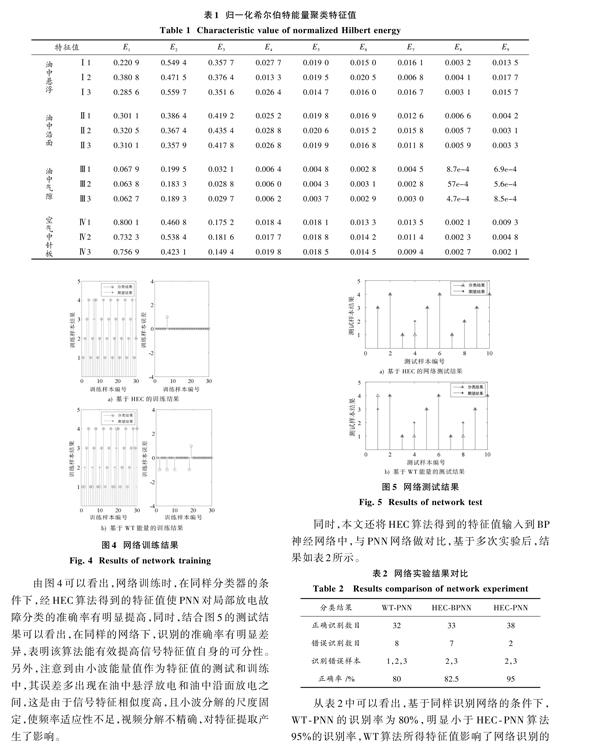
从表2中可以看出，基于同样识别网络的条件下，WT?PNN的识别率为80%，明显小于HEC?PNN算法95%的识别率，WT算法所得特征值影响了网络识别的正确率，对比识别错误样本后发现，在WT算法下识别错误的样本有三种，而HEC算法可以减少错误样本的识别数量，对于油中悬浮放电和空气中针板放电的识别率能够达到100%;在同样特征值提取算法的条件下，PNN网络对多种类的分类识别准确率要高于BP神经网络，在多分类样本的应用中有明显的优势。

4 结 论

目前，傅里叶变换以及小波等算法已经广泛应用于信号处理，但是其对于非线性和非平稳信号的分析有着固有的缺陷。针对这种情况，本文基于希尔伯特?黄变换分解局部放电信号，并通过希尔伯特能量图谱分析局部放电信号的信号特点，提出希尔伯特能量聚类算法，克服了小波分解尺度不可变的缺陷，提高了特征值自身的可分性，使分类效果更加明显。算法中结合PNN作为局部放电故障识别的分类器，识别效果优于BP神经网络，具有更快的运算识别速度和更高的识别率，同时有着较好的扩展性。

参考文献

[1] 李剑，宁佳欣，金卓睿，等.变压器局部放电在线监测超高频Hilbert分形天线研究[J].电力自动化设备，2007，27（6）：31?35.

LI Jian， NING Jiaxin， JIN Zhuorui， et al. Research on UHF Hilbert fractal antenna for online transformer PD monitoring [J]. Electric power automation equipment， 2007， 27（6）： 31?35.

[2] 王旭，彭畅，张振先.基于EEMD的共振解调技术在列车轴承故障诊断中的应用[J].现代电子技术，2015，38（21）：24?27.

WANG Xu， PENG Chang， ZHANG Zhenxian. Application of EEMD based resonance demodulation technology in train bea?ring fault diagnosis [J]. Modern electronics technique， 2015， 38（21）： 24?27.

[3] DANIKAS M G， GAO N， ARO M. Partial discharge recognition using neural networks： a review [J]. Electrical enginee?ring， 2003， 85（2）： 87?93.

[4] HOZUMI N， OKAMOTO T， IMAJO T. Discrimination of partial discharge patterns using neural network [J]. IEEE transactions on electrical insulation， 1992， 27（3）： 550?556.

[5] 邓雨荣，郭丽娟，郭飞飞，等.引入二代小波的自适应BP神经网络局部放电故障识别[J].电力建设，2013，34（6）：87?91.

DENG Yurong， GUO Lijuan， GUO Feifei， et al. Partial discharge fault identification by using adaptive BP neural network based on second generation wavelet [J]. Electric power construction， 2013， 34（6）： 87?91.

[6] 任先文，薛雷，宋阳，等.基于分形特征的最小二乘支持向量机局部放电模式识别[J].电力系统保护与控制，2011，39（14）：143?147.

REN Xianwen， XUE Lei， SONG Yang， et al. The pattern recognition of partial discharge based on fractal characteristics using LS?SVM [J]. Power system protection and control， 2011， 39（14）： 143?147.

[7] 袁国森，张彼德，李明昆，等.基于极值比值法和神经网络的逆变器故障诊断[J].电测与仪表，2016（14）：34?38.

YUAN Guosen， ZHANG Bide， LI Mingkun， et al. Fault diagnosis for inverter based on extremum value ratio and probabilistic neural network [J]. Electrical measurement & instrumentation， 2016（14）： 34?38.

[8] 卢丽.EMD方法在局部放电超声信号提取中的应用[J].现代电子技术，2009，32（3）：137?139.

LU Li. Application of EMD method in extracting ultrasonic signals of transformer partial discharge [J]. Modern electronics technique， 2009， 32（3）： 137?139.

[9] 许峰，李开成，王可.基于EMD和卡尔曼滤波的振荡信号检测[J].电测与仪表，2015，52（24）：60?64.

XU Feng， LI Kaicheng， WANG Ke. The detection of oscillation signal based on EMD and Kalman filter [J]. Electrical measurement & instrumentation， 2015， 52（24）： 60?64.

[10] 李成榕，王彩雄，唐志国，等.基于聚类分析的变压器局部放电智能诊断的研究[J].华北电力大学学报（自然科学版），2008，35（6）：7?12.

LI Chengrong， WANG Caixiong， TANG Zhiguo， et al. Study of intelligent diagnosis of transformers partial discharge based on cluster analysis [J]. Journal of North China Electric Power University （natural science edition）， 2008， 35（6）： 7?12.

[11] PERERA N， RAJAPAKSE A. Recognition of fault transients using a probabilistic neural?network classifier [J]. IEEE tran?sactions on power delivery， 2011， 26（1）： 410?419.