动力松弛法在应变软化类结构有限元静力分析中的应用

，

(同济大学 土木工程学院，上海 200092)

(Δλnfref)TΔan > 0

1 引 言

静力平衡路径是结构受力分析的重要内容。位移有限元法是结构受力分析的重要手段，增量法是结构非线性有限元受力分析的关键[1]。应变软化类结构的静力平衡路径具有荷载峰值点及下降段，一直是分析难题[2]。混凝土是土木工程中应用十分广泛的应变软化材料。

隐式静力算法ISA(Implicit Static Algorithm)、显式拟静力算法EQSA(Explicit Quasi-Static Algorithm)[3]和动力松弛法DRM(Dynamic Relaxation Method)是结构有限元静力分析的三种方法。

ISA主要分为荷载控制类、位移控制类和弧长控制类。对于荷载控制类，可从数学上证明[4]总体刚度矩阵K的非正定或者结点位移a的非稳定性，使得荷载控制类的ISA(Newton法、修正Newton法、准Newton法和广义Newton法)难以进行荷载峰值点捕捉、平衡路径下降段分析及局部失稳分析。对于位移控制类，较荷载控制类，其通常具有更好的收敛率，K的非奇异性可能使之跨越荷载峰值点[5]；但是其局限性在于,K的不对称和不呈带状特征增加了计算成本，需要正确选定敏感度高的位移分量作为控制位移[6]，不能跟踪具有跳回现象的静力平衡路径[7]，不适合应变软化结构的静力分析[5]。对于整体弧长控制类——约束方程包括所有自由结点的位移增量[8]，一般应用于比例加荷载控制的静力问题分析，其通常能跨越平衡路径峰值点并进行后续平衡路径分析[7]，但难以完成具备局部失稳的情形(应变软化及局部屈曲)或平衡路径分支点的结构的静力分析[3]。为了进行应变软化结构的静力分析，May等[9]提出了局部弧长法，将结构划分为损伤区、破坏区和失效区，约束方程仅包括破坏区和失效区自由结点的位移增量[9]。从实际分析看，局部弧长法能进行应变软化结构的静力分析，但现有算例主要考虑受拉应变软化情形[8,9]；另外，在增量迭代中需依破坏区和失效区的扩散情形更新约束方程。

对具备局部失稳情形的结构，文献[3]建议采用显式动力算法EDA(Explicit Dynamic Algorithm)，将静力分析近似处理为拟静力分析。不同于隐式算法，EQSA采用显式时间积分算式进行a的向量式更新，可规避K的构造、求逆及后续的平衡迭代[5]。EQSA也存在局限性，EQSA为有条件稳定算法——稳定求解依赖于离散模型的最小单元尺寸(假设单元物理属性一致)[3]，从而增加了含有小尺寸单元的模型的计算成本；合理的拟静力解要求降低加载速率，但是相应地会增加时间步数(计算成本)；提高加载速率会在加载响应中引入噪音(不可忽略的惯性效应)[3]，甚至使得计算结果完全偏离试验结果[10]；为了降低计算成本而进行的结点质量缩放也可能在加载响应中引入噪音[3]；粘滞阻尼系数的确定具有较强的经验依赖性[3]。

DRM也采用显式时间积分算式进行a的向量式更新，通过虚拟动力过程的动能耗散获得静力解，包括粘滞阻尼型和动态阻尼型[11,12]。DRM可采用虚拟质量和动态阻尼，从而规避EQSA中计算成本依赖于模型小尺寸单元和粘滞阻尼系数确定依赖于分析经验的问题。随着DRM在结构静力分析的应用范围逐渐扩大，近年来常应用于张拉结构的分析中[13，14]。文献[15]采用粘滞阻尼DRM对土体进行了承载力计算，其中土体采用具有应变软化特征的弹塑性本构模型，虚拟质量由虚拟密度构造，虚拟阻尼取仅考虑质量矩阵项的瑞利阻尼；文献[16]进行了类似的工作。文献[17]比较了12种按不同方法附加虚拟阻尼的DRM在框架及桁架结构静力分析中的计算成本，结果表明动态阻尼DRM(DRM by using kinetic damping,kDRM)的计算成本最少。但针对采用具有应变软化特征的损伤本构模型的结构，使用DRM进行静力计算方面，却较少见诸于文献。

本文针对采用具有应变软化特征的损伤本构模型的结构，采用kDRM进行静力平衡路径计算。首先给出问题描述，然后分两个层次阐述基于kDRM的结构静力问题求解过程，随后描述两个算例及相应的计算结果，最后给出讨论和结论。

2 问题的描述

本文求解的固体静力问题属于边值问题。材料应变软化的判别式为[18]

(1)

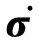
结构在非线性有限元静力分析时，全部自由度可分为加载自由度和未加载自由度两部分，其中前者施加外部结点荷载，后者不施加外部结点荷载。本文主要采用比例加荷载方式进行结构的非线性有限元静力分析。假定固体边界受到足够约束，使其不能产生刚体位移并成为几何不变体系，基于全部自由度建立待求解的非线性平衡方程组为

Ψ(λfref,a) =λfref-p(a) =0

(2)

式中fref为外部结点荷载参照向量，λ为外部结点荷载系数，a为结点位移向量，p为内部结点荷载向量，fref，a和p均为r维向量，r即为系统的自由度，Ψ为结点残值荷载向量。p的计算式为[1]

(3)

式中B为nσ×r阶应变矩阵，σ为nσ×1阶应力向量，nσ为σ内的元素数，Ω为固体所占空间。

对于问题(2),加荷载求解时，λ为已知量，a为待求量；加位移求解时，选取第I个自由度的位移aI为加载位移并为已知量，λ及a中除aI外的元素为待求量。

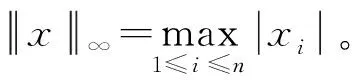
3 问题的求解

本文采用增量法求解静力问题(2)；采用kDRM求解增量步，kDRM求解时包含若干个施加动态阻尼运动的过程。其中，施加动态阻尼的方法是置离散动力系统动能极大值时刻的结点速度向量为0。

3.1 静力问题的增量解法

采用增量法总体上求解静力问题(2)时，增量步n的解为状态量λn,an和Cn。状态量λn，an和Cn中的εn和σn可写为

λn= Δλn+λn -1,an= Δan+an -1

εn= Δεn+εn -1,σn= Δσn+σn -1

(4)

式中 Δλn为外部结点荷载系数增量，Δan为结点位移增量，Δεn为应变增量，Δσn为应力增量。

序列{λn},{an}和{Cn}的求解要点为

(1) 增量步1施加前的λ0= 0和a0=0，C0内的ε0=0，σ0=0和s0为相应初值，上述量满足式(2)。

(2) 增量步n(n≥1)的未知解λn,an和Cn基于已知解λn 1，an 1和Cn 1，通过加荷载增量Δλ或位移增量ΔaI，由kDRM迭代求解。kDRM求解方法详见3.2节。记i为迭代步序号，加荷载求解时，为常量；加位移求解时，为常量。对于kDRM求得的和

a) 若满足收敛判据

(5)

(Δλnfref)TΔan> 0

(6)

则表明解位于平衡路径的硬化段，后续的增量步n+1采用加荷载求解。

(7)

则认定λnfref临近或超越静力平衡路径荷载峰值点，此时重启增量步n的求解，并转换为加位移求解；式(7)中c2为限值，其取值依据为结构的几何容限，即在几何上某单元的应变已超过峰值应变而进入下降段的判据。

(3) 默认先加荷载增量求解增量步1。

3.2 增量步的kDRM解法

在kDRM中实现动态阻尼的方法为[22]，通过监测无阻尼质点系统的动能变化，循环执行在动能极大值时刻先置0结点速度再重启无阻尼运动，直至满足静力平衡条件。本文记kDRM的第k个循环为Dk。kDRM求解增量步n时，其内Dk的控制方程和初始条件为

(8)

式中tk 1和tk分别为Dk的起始时刻和结束时刻，Mn为对角质量矩阵，为结点速度，为结点加速度，和Ctk -1n为初始条件值。问题(8)中各参数及变量(除an(t)外)的确定方法如下。

(1)tk等于按上述控制方程和初始条件，在t>tk -1上算得的第1个动能极大值时刻；同时tk为Dk +1的起始时刻。

(2)tk -1等于Dk -1的结束时刻；k= 1时，tk 1= 0，即为增量步n的加荷载或加位移时刻。

(3)Mn为已知常量。

(4) 对于an(t),若加荷载求解，其内所有元素为基本未知变量；若加位移求解，则加位移的第I个自由度的位移an,I为已知常量，

an,I= ΔaI+an -1,I

(9)

an(t)中除an,I外的其余元素为基本未知变量。

(5)Cn(t) 为未知变量，其内的εn(t) =Ban(t)，sn(t)是εn(t)的函数，σn(t)是sn(t)和εn(t)的函数，故Cn(t)是an(t)的函数。

(6)pn(t)为未知变量，由式(3)计算，是an(t)的函数。

(7) 对于λn(t)，若加荷载，λn(t) 为已知常量，

λn(t) = Δλ+λn 1

(10)

若加位移，λn(t)为基本未知变量，

λn(t) =pn,I/fref,I

(11)

式中fref,I和pn,I分别为fref和pn(t)内与第I个自由度对应的元素值，λn(t)是an(t)的函数。

由上述分析知,给出问题(8)中an(t)的计算式是完成增量步n的kDRM求解的关键。问题(8)描述的动力问题具有非线性，an(t)由显式时间积分法求解[3]。本文选用中心差分算法CFDM(Central Finite Difference Method)求解问题(8)。

CFDM求解问题(8)前，需利用CFDM的稳定条件确定Mn及离散时间域的固定时间增量h。Barnes给出的CFDM稳定条件为[14]

(12)

式中mj和kj max分别为第j个结点的质量和沿坐标轴各方向位移刚度最大值。确定kj max后，在满足式(12)的情况下，h可取任意值。本文通过给第j个结点施加微小位移后计算相应结点荷载的方式估算kj max，并取

mj= max(c3kj maxh2/2,mmin)

(13)

由式(12)可得c3是一个值大于1的系数。CFDM的收敛速率及是否收敛与c3的取值有关，通常收敛速度随c3增大而减小，遇到不收敛情形时可增大c3[23]。文献[24]取c3= 4后，采用动态阻尼DRM跟踪强几何非线性的张拉结构静力平衡路径。mmin为结点质量下限值，其功能为避免因结构局部区域负刚度而产生负质量；mmin可取一个适当小的经验值，较小的mmin可加速负刚度区域的单元结点逼近静态。本文按式(13)逐结点算得mj后构造Mn。

(14)

式中ik 1为Dk的起始时刻序号，的计算式为

(15)

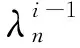
4 算 例

算例1模型I为一个3根拉杆组成的平面桁架，如图1所示。拉杆截面积A均为1 mm2。分析时将每个拉杆划分为4个单元，单元类型为二结点线单元。单元形函数为一次多项式。通过计算单元轴向应力σl,由直接平衡法精确计算p；用于确定σl的单元轴向应变εl= (l-lini)/lini，其中lini和l分别表示未变形的和已变形的单元轴向长度。

模型I采用一种虚构的、依赖加载历史以及受拉应变软化的一维非弹性损伤本构模型：

(16)

式中εl,un和σl,un分别表示材料点在加载历史中所达到的最大拉应变值及相应的拉应力值。应力应变关系如图1所示。

模型I的加载结点编号和加载自由度如图1所示。采用kDRM求解比例加荷载增量下的平衡路径时，h=0.1 s，c1=0.0002，c2=3000 mm，c3=4.0，mmin=0.3 kg， Δλ=1，其余分析参数的配置列入表1。当3根拉杆中都存在εl>1.4的单元时(对应的σl<0.0056 N/mm2)，终止增量步分析。图2为模型I内的1号结点在y向的荷载-位移曲线，不仅标识了模型I加载的硬化阶段、若干荷载峰值点及软化阶段，而且标识了因单元软化产生的荷载突变。

算例2模型II为一个轴心受压混凝土构件，如图3所示，构件厚度t=150 mm；分析时x向网格划分方式为4 mm×50 mm；y向网格划分采用IIA，IIB，IIC和IID四种方式，n×l分别为1×600，2×300，3×200和4×150。单元类型为四结点面单元，单元形函数为二次多项式。采用4个高斯积分点近似计算p。

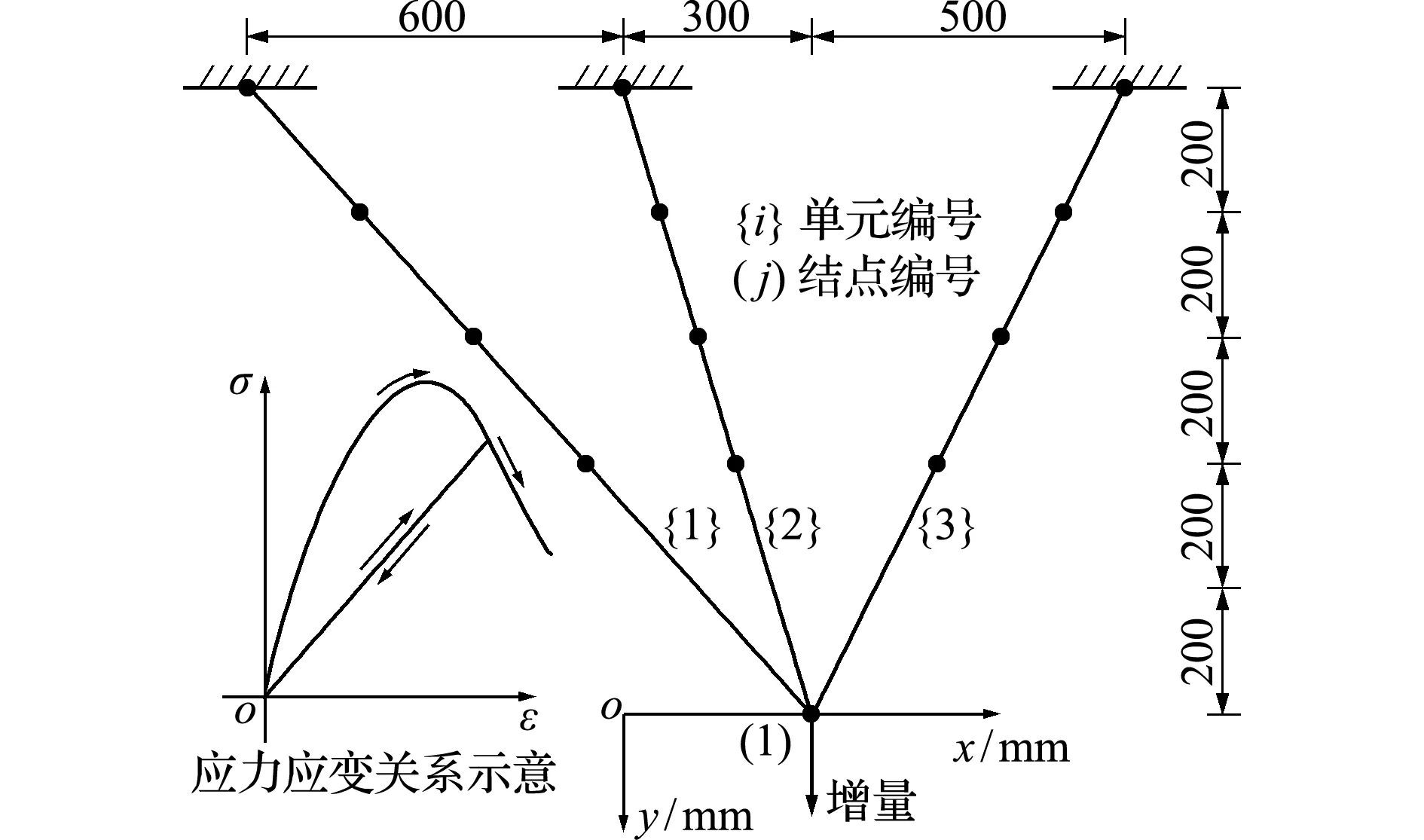
图1 模型I的几何、离散信息和应力应变关系

Fig.1 Model I:geometry，meshing and illustration of stress-strain relation

图2 模型I的1号结点y向的荷载-位移曲线

Fig.2 Model I:load-deflection curve of node 1 inydirection

模型II采用Mazars[26]提出的单标量弹性损伤本构模型

σ= (1-ω)Diniε

(17)

式中ω为损伤变量，Dini为(各向同性)初始刚度矩阵。Dini由弹性模量E和泊松比ν构造。ω的算式为

ω=max(ωmax,α+ω++α-ω-)

(18)

式中ωmax为材料点在加载历史中所达到的最大损伤变量值，α+ω++α-ω-为即时损伤变量，α+和α-为系数，ω+和ω-分别为受拉和受压时的损伤变量。α+和α-依赖于ε，计算式参考文献[26]可知，

(19)

图3 模型II的几何、离散信息和应力应变关系

Fig.3 Model II:geometry，meshing and illustration of stress-strain relation

模型II的加载结点编号及加载自由度如图3所示。模型II为一个轴心受压混凝土构件，本文采用两种方法求解。一种即采用上文已详述的比例加荷载增量求解(解法a)；另一种采用先比例加荷载增量，再比例加等位移增量求解(解法b)；其中，前者求解峰值点前的平衡路径，后者求解峰值点后的平衡路径。比例加等位移增量即对加载自由度施加相等位移增量，求解时的平衡方程组为Ψ(fn,an) =fn-p(an) =0，其中fn为外部结点荷载向量。Ψ(fn,an) =0求解时,非加载自由度上的荷载增量Δfα=0，而位移增量Δaα为未知量，加载自由度上的荷载增量Δfβ为未知量，而位移增量Δaβ为已知量。由kDRM求解Δaα和Δfβ的流程可通过参考文献[16]构造。本文采用kDRM求解法a和解法b的增量步时，参数h,c1,c2,c3,mmin和Δλ设置相同，取h=0.1 s，c1=0.0002，c2=20 mm，c3=4.0，mmin=0.3 kg，Δλ=1。采用解法a时，其余kDRM分析参数设置列入表1；采用解法b时，求平衡路径上升段时对加载自由度施加的结点荷载增量满足2Δf1y=Δf2y=Δf3y=Δf4y=2Δf5y=10 kN，求平衡路径下降段时对加载自由度施加的结点位移增量满足Δa1y= Δa2y= Δa3y= Δa4y= Δa5y=0.0025 mm。当迭代解fin,3y满足

(20)

时，终止增量步分析。由算后数据发现，解法b结果也满足表1所给出的比例加荷载(fref)要求。图4为模型II内2号和3号结点y向荷载-位移曲线。图例内线型代号的第三个数字代表结点编号，第四个字母表示解法(解法a或解法b)；最后一个收敛解由●标识，满足增量步分析终止条件式(20)，但不满足收敛条件式(5)的迭代解由▼标识。由图4得如下结论。

(1) 荷载峰值点以前，不同网格划分得出相同的平衡路径。

(2) 平衡路径峰值点位移值和荷载值接近估算值(设a1y=a2y=a3y=a4y=a5y，2f1y=f2y=f3y=f4y= 2f5y)，即εc×(n×l) =1.05 mm，fcA=24.4×200×150/4=183 kN。

图4 模型II的i号结点y向荷载-位移曲线(i=2,3)

Fig.4 Model II:load-deflection curve of nodeiinydirection (i=2,3)

(3) 荷载峰值点之后，不同网格划分下的同一结点给出不同平衡路径。比例加荷载增量求解时，同一网格划分下的不同结点给出不同的下降段平衡路径；比例加等位移增量求解时，同一网格划分下的不同结点给出相同的下降段平衡路径(此由算后数据可知，图4仅给出了3号结点平衡路径)。网格划分越细，下降段平衡路径越陡。上述符合固体因材料应变软化进而局部化形变而产生的静力解非唯一性现象[1]。对于比例加荷载情形，在荷载峰值点之后，当λ随增量步递减时，加荷载控制的自由度可能会出现snap back现象(如IIB2a)，其根源在于此类自由度附近的积分点出现应变卸载，当然加位移控制自由度附近的积分点依旧为应变加载。

5 讨 论

(1) 模型I采用一种人工构造的一维应变软化损伤本构模型对一个简单平面桁架完成了静力平衡路径的求解。但是，求解增量步的kDRM基于普适的热力学第一定律构造，即力学系统外势能、内势能和动能之间的相互转换规律及动能耗散规律。因此，在应用上可不受到材料本构和单元类型限制，可进一步探索其在由实验标定的本构模型的常见结构静力分析中的应用。

(2) 模型II采用Mazars单标量弹性损伤本构模型，应力应变关系式简洁、光滑，但其不能很好反映多轴应力状态下的本构关系[27]；为了更为真实反映混凝土材料在复杂情况的拉压不等性和单边效应特征[28]，后续可尝试采用双标量弹性损伤本构模型或双标量弹塑性损伤本构模型进行混凝土构件(梁、柱或墙)的静力分析。对于应变软化结构静力解的网格依赖性问题，可尝试采用非局部方法和集中非连续方法进行处理[1]。

(3) 对模型I、模型II进行加荷载增量和加位移增量分析时，采用固定的Δλ和ΔaI求解，尚未反映出结构的刚度变化特征，后续工作中可引入依增量步变化的Δλn和Δan,I，从而使得计算过程兼顾平衡路径的光滑性及求解高效性。

6 结 论

本文首次提出用动力松弛法求解应变软化结构的非线性有限元静力分析问题。本文从总体和增量步两个层次详细阐述了结构非线性有限元静力问题的DRM解法完成了两个数值试验得出如下结论。

(1) 通过引入虚拟质量、虚拟阻尼和虚拟时间过程使得原静力问题变得适定可解，且原静力问题解即为虚拟时间过程的稳态解。

(2) 通过荷载位移增量转换规则、收敛发散判据实现静力平衡路径上升段、极值点和下降段的整体分析。

(3) 无需整体刚度矩阵的组装、求逆计算，相应计算成本的降低使本文方法在大型结构有限元静力分析中较隐式静力算法具有应用优势。

(4) 可完成同时具备几何非线性的应变软化结构的静力分析(模型I)，给出的静力解答具备因材料应变软化而具备的网格依赖性(模型II)。

本文方法解决了应变软化结构全过程静力计算的不收敛问题。

参考文献(References):

[1] Zienkiewicz O C,Taylor R L.TheFiniteEle-mentMethodforSolidandStructuralMechanics(SixthEdition)[M].Elsevier,2005.

[2] 欧进萍.重大工程地震/风致灾变若干关键科学问题研究进展与展望[A].第二届全国防灾减灾工程学术会议[C].哈尔滨，2013.(OU Jin-ping.Disaster evolution of civil infrastructure under strong earthquake and wind [A].The Second National Academic Conference on Disaster Prevention and Reduction Engineering [C].Harbin,2013.(in Chinese))

[3] Dassault systemes simulia corp.Abaqus6.14AnalysisUser’sGuideVolumeII：Analysis[M].2014.

[4] H · 卡德斯图赛[德].有限元法手册[M].诸德超，傅子智，等译.北京:科学出版社,1996.(Kardestuncer H,Norrie H.FiniteElementHandbook[M].Translated by ZHU De -chao,FU Zi-zhi,et al.Beijing：Science Press,1996.(in Chinese))

[5] De Borst R,Crisfield M A,Remmers J J C,et al.Non-linearFiniteElementAnalysisofSolidsandStructures[M].John Wiley & Sons,2012.

[6] 何 政，欧进萍.钢筋混凝土结构非线性分析[M].哈尔滨：哈尔滨工业大学出版社,2007.(HE Zheng,OU Jin-ping.NonlinearAnalysisofReinforcedConcreteStructures[M].Harbin:Harbin Institute of Technology Press，2007.(in Chinese))

[7] Crisfield M A.Non-LinearFiniteElementAnalysisofSolidsandStructures,Vol I:Essentials[M].New York:Wiley,1991.

[8] Alfano G,Crisfield M.Solution strategies for the delamination analysis based on a combination of local-control arc-length and line searches[J].InternationalJournalforNumericalMethodsinEngineering,2003,58(7):999-1048.

[9] May I M,Duan Y.A local arc-length procedure for strain softening[J].Computers&Structures,1997,64(1-4):297-303.

[10] Natário P,Silvestre N,Camotim D.Web crippling failure using quasi-static FE models[J].Thin-WalledStructures,2014,84:34-49.

[11] Day A S.An introduction to dynamic relaxation[J].TheEngineer,1965,219:218-221.

[12] Barnes M.Dynamic relaxation analysis of tension networks[A].The International Conference on Tension Structure[C].London,1974.

[13] Newmark N M.A method of computation for structural dynamics[J].JournaloftheEngineeringMe-chanicsDivision,1959,85(3):67-94.

[14] 叶继红,李爱群,刘先明.动力松弛法在索网结构形状确定中的应用[J].土木工程学报,2002,35(6):14-19.(YE Ji-hong,LI Ai-qun,LIU Xian-ming.Form finding of cable nets by modified dynamic relaxation[J].ChinaCivilEngineeringJournal,2002,35(6):14-19.(in Chinese))

[15] Siddiquee M S A,Tanaka T,Tatsuoka F.Tracing the equilibrium path by dynamic relaxation in materially nonlinear problems[J].InternationalJournalforNumericalandAnalyticalMethodsinGeomecha-nics,1995,19(11):749-767.

[16] 彭芳乐,李福林,白晓宇.针对砂土应变软化强非线性问题的动态松弛有限元法研究[J].岩土力学,2012,33(2):590-596.(PENG Fang-le,LI Fu-lin,BAI Xiao -yu.A dynamic relaxation-finite element method for strong nonlinearity caused by post-peak strain softening of sands[J].RockandSoilMechanics,2012,33(2):590-596.(in Chinese))

[17] Rezaiee-Pajand M,Sarafrazi S R,Rezaiee H.Efficiency of dynamic relaxation methods in nonlinear analysis of truss and frame structures[J].Computers&Structures,2012,112:295-310.

[18] Drucker D C.A definition of stable inelastic material[J].J.Appl.Mech,1957,26:101-106.

[19] De Borst R,Sluys L,Muhlhaus H B,et al.Fundamental issues in finite element analyses of localization of deformation[J].EngineeringComputations,1993,10(2):99-121.

[20] 维诺格拉多夫,等.数学百科全书(第3卷)[M].数学百科全书编译委员会.北京：科学出版社,1997.(Vinogradov,Ivan Matveevich,Adian,S.I,et al.Математическая энциклопедия(Vol.3)[M].Translated by Mathematics Encyclopedia Compilation Committee.Beijing：Science Press,1997.(in Chinese))

[21] Ye J H,Feng R Q,Zhou S L.The modified dynamic relaxation method for the form-finding of membrane structures[J].AdvancedScienceLetters,2011,4(8-9):2845-2853.

[22] Nabaei S S,Baverel O,Weinand Y.Mechanical form-finding of the timber fabric structures with dynamic relaxation method[J].InternationalJournalofSpaceStructures,2013,28(3-4):197-214.

[23] 祖义祯,邓 华,王 玮.基于显式弧长法的索杆张力结构成形过程数值模拟[J].空间结构,2015,21(1):90-96.(ZU Yi-zhen,DENG Hua,WANG Wei.Numerical simulation of the erection process of cable -strut tensile structures using explicit arc -length me -thod [J].SpatialStructures,2015,21(1):90-96.(in Chinese))

[24] Ali N B H,Rhode-Barbarigos L,Smith I F C.Analysis of clustered tensegrity structures using a modified dynamic relaxation algorithm[J].InternationalJournalofSolidsandStructures,2011,48(5):637-647.

[25] Zienkiewicz O,Taylor R,Zhu J.TheFiniteElementMethod:ItsBasisandFundamentals(SixthEdition)[M].Elsevier,2008.

[26] Mazars J.A description of micro—and macroscale damage of concrete structures[J].EngineeringFractureMechanics,1986,25(5-6):729-737.

[27] 李 杰,任晓丹.混凝土静力与动力损伤本构模型研究进展述评[J].力学进展,2010,40(3):284-297.(LI Jie,REN Xiao -dan.A review on the constitutive model for static and dynamic damage of concrete[J].Advancesinmechanics,2010,40(3):284-297.(in Chinese))

[28] Comi C,Perego U.Fracture energy based bi-dissipative damage model for concrete[J].InternationalJournalofSolidsandStructures,2001,38(36-37):6427-6454.