基于算法复杂度理论的拟力法计算效率评价
, , 宏男,2
(1.大连理工大学 海岸和近海工程国家重点实验室,大连 116024;2.沈阳建筑大学 土木工程学院,沈阳 110168)
1 引 言
计算效率是衡量算法性能的重要指标,其评价方法通常分为实践和理论两个方面。实践方面指对算法进行数值试验得到其运行时间,而时间受计算机性能等因素影响,很难直接判断算法本身的优劣。理论方面指算法的复杂度分析,即分析算法运行所需的计算机资源,该理论是计算机科学家提出的[1],目的是建立分析算法的理论模型,使得算法效率的评价不依赖于计算机系统。目前,该方法应用于诸多领域中来进行算法效率评价。在计算机领域,韩忠明等[2]提出了一种新的面向热点话题时间序列的有效聚类算法,并对比分析了新方法和传统方法的时间复杂度,结果表明新方法的时间复杂度更低,效率更高。李伟等[3]对网络环境下已有的资源查找方法进行复杂度分析,评价了各方法的效率,指出了各方法的优缺点,为进一步改进算法提供理论依据。在结构重分析方面,杨志军等[4]用算法复杂度理论分析了基于Epsilon算法的自适应迭代法,并与组合近似方法比较,证明了该算法的高效性。Deng等[5]提出了虚拟荷载结构重分析法,并与传统结构分析法进行算法复杂度比较,结果表明虚拟荷载法计算量更小,提高了计算效率。在通信与信息系统方面,梁晓雯[6]提出了正交频分复用(OFDM)系统中自适应分配算法,并将该算法的复杂度与经典算法比较,证明了该方法计算量更小,效率更高。在多体动力学方面,胡景晨等[7]提出了一种算法复杂度为O(n)的递推绝对节点坐标法,并证明了该方法是一种高效的非线性大变形多柔体系统求解方法。在微波和光学领域,Zhao等[8]提出了一种新的时域有限差分法,通过算法复杂度分析证明了该方法比传统方法减少了50%的乘法计算量。在多元统计质量控制方面,Sharif等[9]用算法复杂度分析方法对已有的两种测试方法——广义方差法和向量方差法进行了效率评价。
拟力法是一种高效的结构非线性分析方法,与传统变刚度法相比,该方法在每个非线性迭代步中无需对整体刚度矩阵重新合成分解,有效改善了传统方法的效率。拟力法的特点是在结构非线性分析过程中引入局部塑性机制,将变形分解为弹性和塑性两个部分,用塑性变形反映结构非线性变化,而结构整体刚度矩阵在求解过程中始终为弹性刚度矩阵。拟力法的基本思想由Lin[10]提出,Wong等[11]首次将该方法用于框架结构的地震反应分析中。近年来,拟力法在地震反应能量分析[12-14]、结构抗震性能评估[15]、消能减震[16,17]、振动控制[18]以及结构精细化分析[19]等方面取得了进展。研究表明,拟力法在结构非线性分析方面有很高的求解效率,对其评价是通过与有限元分析软件(如ANSYS、SAP2000等)的计算时间进行对比[16,17,20],由于分析平台不同,得到的计算时间会受软件性能和程序代码效率等不可控因素的影响,因此时间只能定性判断算法效率,并不能作为定量的评价指标。
本文基于算法复杂度分析理论对拟力法进行效率评价,并与传统变刚度法对比分析。给出了采用两种方法计算非线性迭代步时的算法时间复杂度函数,从数学角度揭示了拟力法在分析结构非线性问题时的高效性。
2 计算效率评价理论
算法效率评价方法包括事前估算和事后测试[21]。事后测试是指用程序实现算法后,测算其时间和空间的消耗,这种测试方法易受外在因素影响,如计算机系统、分析软件、编程语言以及编程代码效率等,如果不能保证上述条件相同,则很难精确评价算法的计算效率。计算机系统、分析软件及编程语言一般容易实现统一,而程序代码效率则不容易控制,同一算法不同程序员编程,其运行时间通常不同,因此无法确定算法效率的评价标准。此外,算法的计算时间不仅包括基本运算的执行时间还包括数据读写的时间,数据读写量较大,这部分占用的时间可能会掩盖算法的真实性能,因此从算法运行时间不能精确评价其效率。事前估算是指对算法进行复杂度分析,即统计算法运行所需的计算机资源,包括时间复杂度和空间复杂度[21]。算法时间复杂度指算法运行所需的计算工作量,是问题规模的函数,算法的时间复杂度越低,算法的效率越高;空间复杂度指算法运行所需的储存空间。随着计算机的快速发展,算法消耗的内存可通过提升硬件性能来解决,因此时间复杂度是影响算法性能的主要因素,本文的算法复杂度分析指的是算法时间复杂度。
2.1 时间复杂度分析理论
算法时间复杂度可从运行算法的实际计算机中抽象出来,该量化结果不依赖于计算机。采用数学理论来建立时间复杂度函数,其定义如下[21]。
设I为一个算法某次运行时的输入数据,规模为k,则算法的时间复杂度T是k和I的函数,记为T(k,I)。将算法执行步骤拆分为加法、减法、乘法、除法和赋值等基本运算,每种基本运算的执行次数为ei,ei也是k和I的函数,记为ei(k,I),执行这些基本运算的时间分别为ti,则有
(1)
式中T(k,I)为算法时间复杂度函数;ti为基本运算的抽象时间,并非实际运行时间;l为基本操作数目。
显然,在算法时间复杂度分析时,无需统计所有基本操作数,只考虑有代表性的基本操作即可,这里只将四则运算(加、减、乘和除)作为基本操作[22]。现如今,计算机执行加减运算和乘除运算的速度相差很小[23],因此认为四则运算的计算时间相同,则时间复杂度函数可简化为
(2)

通常,算法时间复杂度可从最优、平均及最差三个方面加以区分。算法最优时间复杂度表示算法最好情形的性能,由于此情况出现概率小,所以不能代表典型的结果。而算法平均复杂度通常能反应典型的结果,但分析比较麻烦。最常用的是算法最差时间复杂度,代表算法最坏情形的性能,虽然此情况出现概率也较小,但是能够给出算法复杂度的上界,是算法性能的保证。其数学表述如下[25]。
设T(k)和f(k)是以k为变量的函数,若存在正常数c和k0,使得当k≥k0时T(k)≤cf(k),则称函数f(k)是函数T(k)的上界,记作
T(k)=O[f(k)]
(3)
式中O[f(k)]为算法的渐进时间复杂度,可简称为时间复杂度,O为量级。
综上所述,算法的时间复杂度通常用两种方法表示,一种是根据定义得到时间复杂度函数g(k)的完整形式;另一种是用g(k)的高阶项O[f(k)]表示,即算法渐进时间复杂度,反映算法复杂度的增长速率。g(k)的函数类型决定了算法的类型,若g(k)为多项式函数,则该算法为多项式算法,若g(k)为指数函数,则该算法为指数算法。
2.2 降低算法复杂度的方法
根据2.1节理论可知,算法时间复杂度分析即为分析算法的计算量。在分析过程中,可采取适当的方法减少计算量,达到降低算法复杂度的目的。
(1) 选择合适的计算顺序
同一个算法选择不同的计算顺序,其复杂度不同。当计算两个标量与矩阵(或向量)相乘时,若将两个标量分别与矩阵(或向量)相乘,需要进行两次标量与矩阵(或向量)的乘法运算;若运用结合律,先计算两个标量乘积,再将得到的新标量与矩阵(或向量)相乘,则只需一次标量与矩阵(或向量)的乘法运算,比前一种方法节省大约一半的计算量。因此,在类似的矩阵与向量相乘的运算中,可通过乘法结合律,选择不同的计算方式,达到减少计算量的目的。
(2) 考虑计算对象的特殊性
当计算两个有对称稀疏特性的方阵相乘时,若不考虑其特殊性(即按满阵计算),时间复杂度为O(p3)(p为矩阵阶数);若考虑对称稀疏性,使零元素不参与计算,并且只计算矩阵中一半元素值,时间复杂度为O(p2),比前一种方式降低一个数量级,如果矩阵规模很大,则考虑计算对象特殊性会显著降低算法复杂度。
由上述分析可知,在数学上等价的表达式,采用不同的计算次序,算法复杂度不同;如果计算对象有特殊的性质(稀疏性、带状性及对称性等),在计算中考虑其特殊性与否对算法复杂度影响显著。因此,在计算之前对算法不同实现方式进行复杂度分析,找到最经济的计算方式是必要的。
3 拟力法计算效率评价
3.1 拟力法基本原理
拟力法求解结构非线性问题的核心思想是将材料的应变进行弹塑性分解,引入局部塑性刚度矩阵。在求解过程中,结构的整体刚度矩阵保持为弹性刚度矩阵不变,用局部塑性刚度矩阵和塑性变形反映结构非线性变化。虽然结构整体刚度矩阵不必实时更新和分解,但是引入的塑性应变是附加的未知量,为了解决该问题,借鉴传统有限元建立单元位移场的思想,在单元内设置塑性插值点来获得塑性应变的分布形式。根据虚功原理和塑性插值点处的内力平衡条件建立拟力法的单元控制方程,再对各单元位移和荷载增量集成得到结构整体控制方程,最后对方程进行迭代求解[19]。基本计算步骤可总结如下。
(1) 建立单元位移场及塑性应变场。
(2) 建立单元结点位移和荷载的增量方程。
(3) 合成整体结点位移和荷载的增量方程。
(4) 迭代求解整体控制方程得到结构结点位移增量。
对于步骤(4),由于在非线性分析过程中结构通常只有少部分产生塑性变形,因此大多数塑性插值点处的变形为零,此时将整体控制方程中与这些插值点对应编号的行和列消去不会影响求解结果[19]。可见,在每步迭代过程中,首先需要对塑性插值点处的塑性自由度进行状态判断,然后根据判断结果对控制方程进行消元,最后对消元后的方程求解得到结构结点位移。
3.2 拟力法的控制方程求解
由3.1节可知,由于拟力法引入了局部塑性刚度矩阵,使其在结构结点位移的求解与传统方法不同。本节以一个位移自由度数为n的框架结构(如图1所示)为例,具体介绍拟力法的控制方程特点和求解过程。
假设图1中一个构件为一个单元,且每个单元有两个塑性插值点,实心插值点代表该处无塑性变形,空心插值点代表该处产生了塑性变形。则在每个非线性迭代步中,消元后的结构控制方程为[19]
(4)


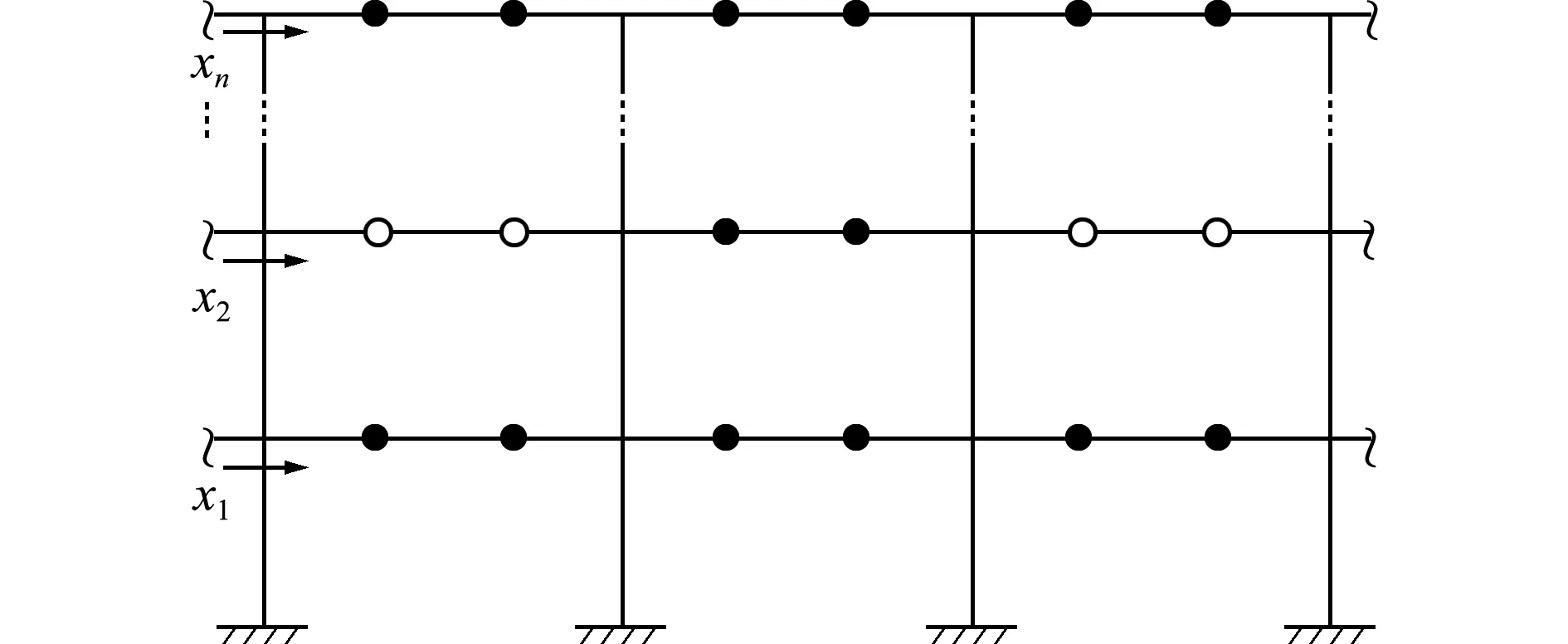
图1n个位移自由度的框架结构
Fig.1 Frame structure withndisplacement degrees of freedom
式(4)表明,由于矩阵K′r和K″r的引入,拟力法控制方程的规模比传统变刚度法大,但是方程的系数矩阵是分块矩阵,对其变换可得
(5)
(6)

(7)
将式(6)进一步写成
ΔX=ΔX1+ΔX2
(8)

(9)
(10)
ΔX1为结构的弹性位移,ΔX2为结构的塑性位移。
而传统变刚度法每个迭代步的控制方程为
KtΔX=ΔF
(11)
由式(5,11)可得
(12)
式中Kt为每步的切线刚度矩阵,规模为n×n阶。
从上述分析可知,拟力法控制方程的求解与传统方法相比有如下特点。
(1) 当结构进入非线性后,虽然拟力法控制方程的规模比传统变刚度法大,但是由于其系数矩阵的分块特点,对其变换后,由式(12)可知,此时系数矩阵的规模仍为n×n阶,与传统方法相同。
(2) 由式(9,10)可知,拟力法中Ke始终为初始弹性刚度矩阵,在求解时只需一次LDLT分解即可。每个非线性迭代步中,需对矩阵Kf重新合成分解,该矩阵规模为d×d阶。由式(11)可知,传统方法每步需更新和分解切线刚度矩阵Kt,该矩阵规模为n×n阶。一般情况下,由于d≪n,因此拟力法每步更新和分解的刚度矩阵规模比传统变刚度法小。

3.3 拟力法的时间复杂度分析

综合上述分析,将拟力法控制方程的具体求解步骤[26]和每步的时间复杂度列入表1。

表1 拟力法的时间复杂度
Tab.1 Time complexity of FAM

计算步骤计算项目时间复杂度(1)ΔX1=K-1eΔF2nm-n-12m2+12(2)Δu0=K'TrΔX12αd-d(3)Kf=K″r-K'TrK-1eK'rβd/2(4)Δu1=K-1fΔu0d3/3+3d2-7d/3(5)Δu2=K'rΔu12αd-d(6)ΔX2=K-1eΔu22nm-n-12m2+12(7)ΔX=ΔX1+ΔX2n合计4mn+d3/3+3d2+4αd+βd/2+1-13d/3-m2-n注:Δu0,Δu1和Δu2为求解式(10)过程中引入的中间变量。
3.4 变刚度法的时间复杂度分析

3.5 对比分析
非线性分析中最耗时的部分是结点位移的求解,也是拟力法和传统方法的主要不同点。对于迭代算法,复杂度不仅取决于一次迭代运算的计算量,还和算法的迭代次数(即算法的收敛速度)有关。假设两种方法计算结点位移时都采用Newton-Raphson方法,即收敛速度相同,只需对两种方法一个迭代步的时间复杂度进行分析。每个迭代步计算流程如图2所示。本节仅针对计算结构结点位移部分进行时间复杂度对比分析,忽略更新刚度矩阵等次要运算的复杂度。
表2 传统变刚度法时间复杂度
Tab.2 Time complexity of conventional method

计算步骤计算项目时间复杂度(1)ΔX=K-1tΔFnm2+8nm+n合计nm2+8nm+n

图2 非线性迭代步计算流程图
Fig.2 Calculation flow charts of nonlinear iteration step
通过3.3节和3.4节的分析可知,针对图2中结点位移求解部分,拟力法的时间复杂度函数为
(13)
传统变刚度法的时间复杂度函数为
T2=nm2+8nm+n
(14)
通过对比式(13,14)可知,两种方法都是多项式算法,当产生的塑性自由度数d远小于结构位移自由度数n时,传统变刚度法的时间复杂度为O(m2n),拟力法的时间复杂度为O(mn),拟力法的复杂度量级低,增长速率慢;当d值较大时,拟力法的时间复杂度为O(d3)。若T1=T2,认为拟力法的计算效率达到上限,产生的塑性自由度数目为理论最大值:
(15)
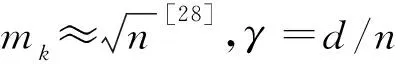
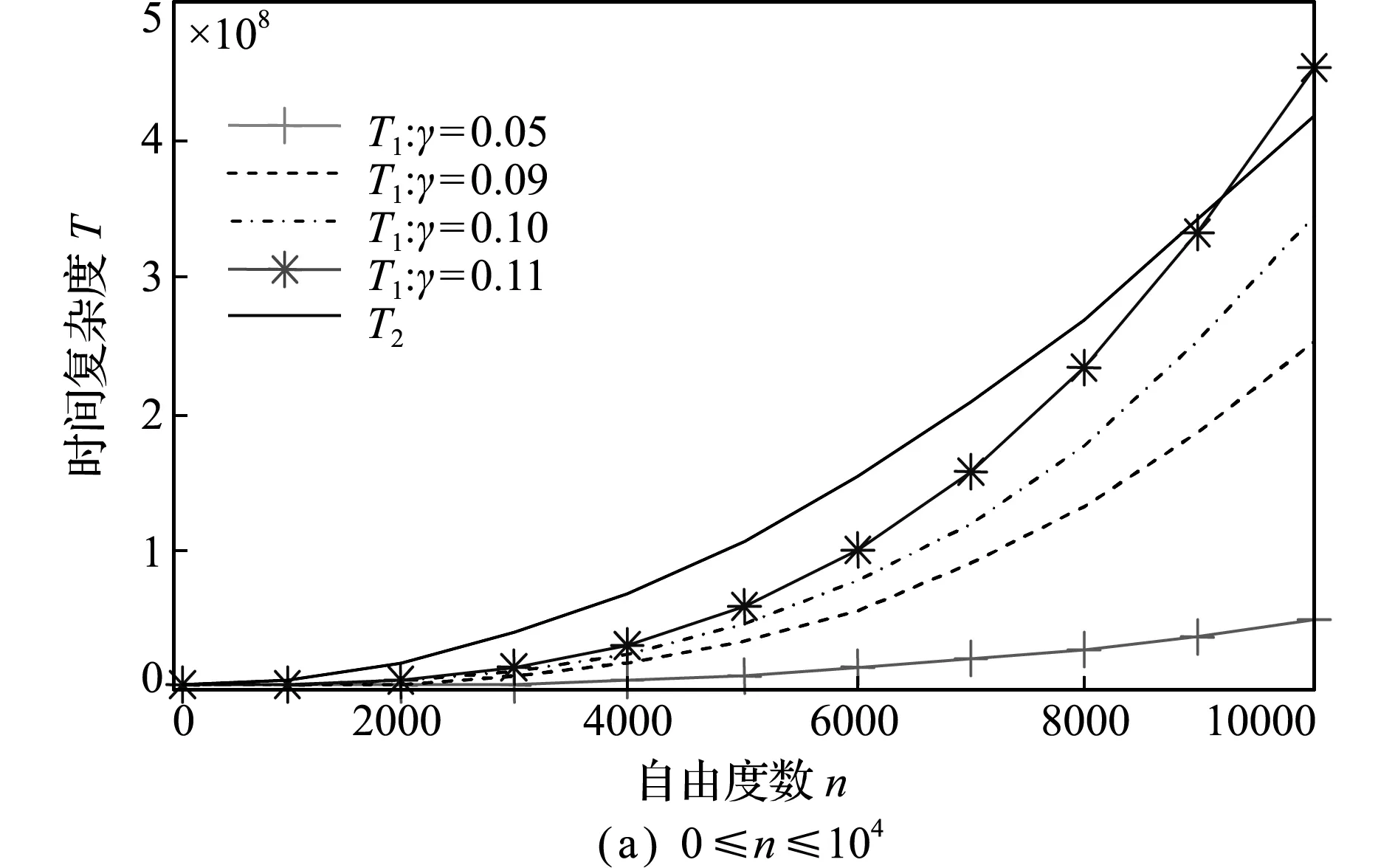

图3 拟力法和传统变刚度法的时间复杂度对比图
Fig.3 Comparison of the time complexity of FAM and conventional method
从图3可以看出,当结构自由度数相同时,产生的塑性自由度数越多,拟力法的时间复杂度越高;产生的塑性自由度数越少,拟力法的效率优势越大。当塑性自由度数小于理论最大值(即图中曲线交点对应的塑性自由度数)时,拟力法的复杂度低于传统方法。从图4可以看出,随着n的增大,γmax减少。对于不同规模的结构,进入非线性区域的比例不超过γmax,即可保证拟力法每步计算的效率优势。图4(a)中,当n较小时,γmax≥50%;当n≤5000时,γmax≥15%;当5000≤n≤10000时,10%≤γmax≤15%;图4(b)中,当104≤n≤5×104时,γmax≥6%;当5×104≤n≤105时,γmax≥5%。通常情况下,在非线性分析过程中,结构进入塑性的区域较小,因此γ达到最大值的概率较小,即使有少数迭代步达到最大值,只能说明拟力法该步的效率低于传统方法,在其余迭代步中拟力法的复杂度仍低于传统方法,因此不会影响整个分析过程的计算效率。
4 算例分析
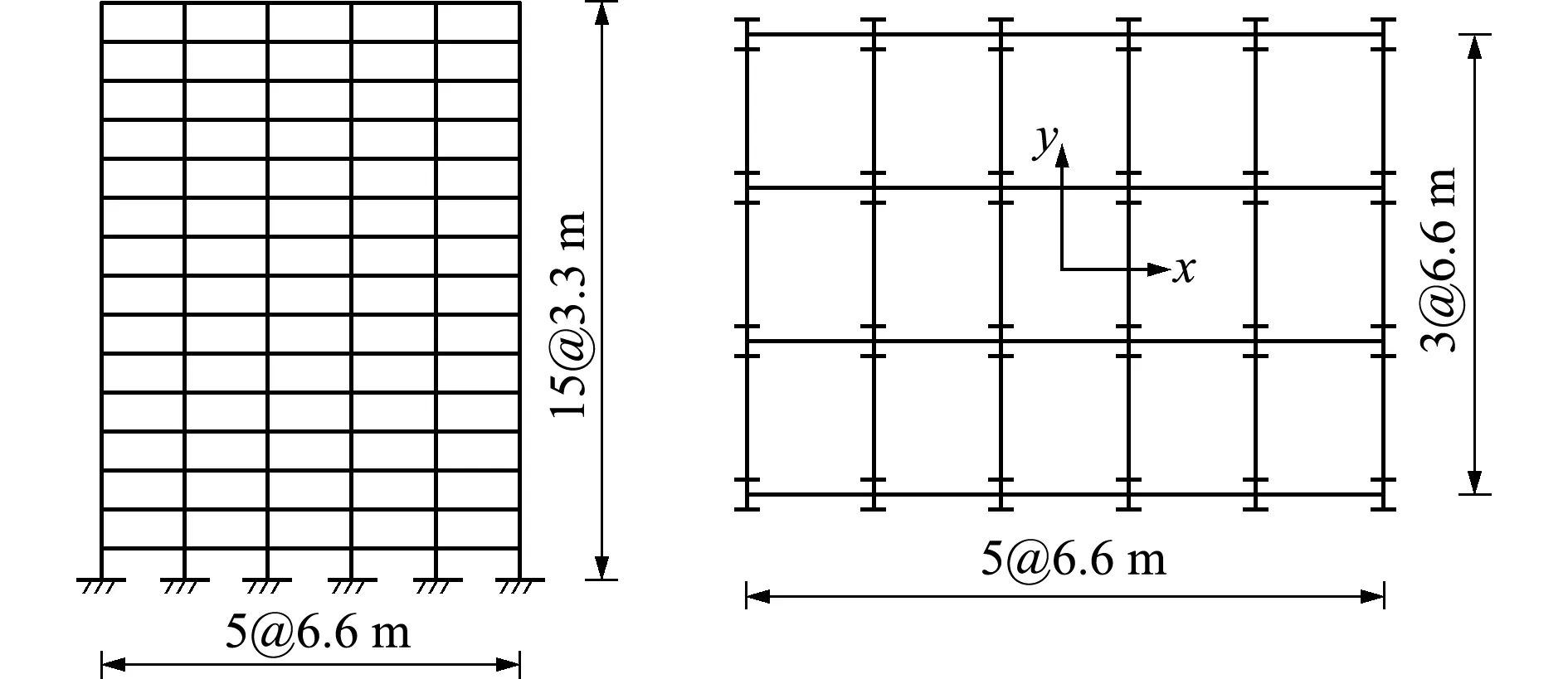
4.1 工程概况
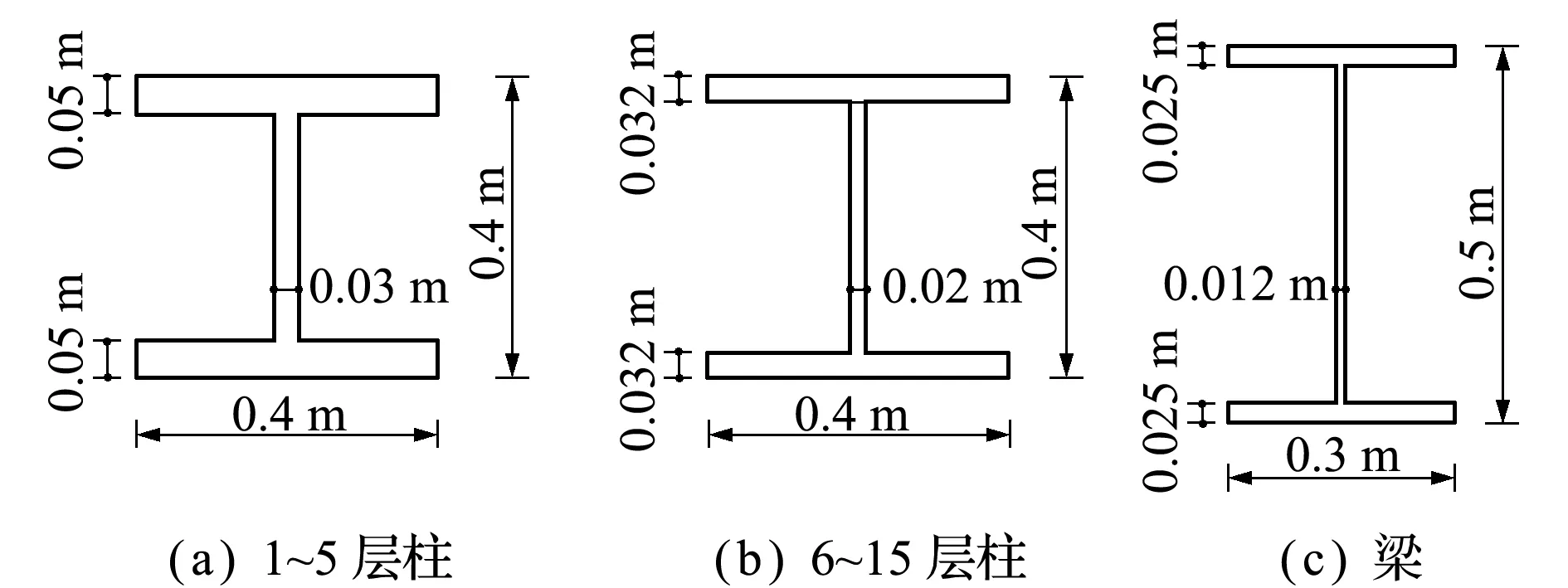
某15层钢框架结构,如图5所示,每层质量为800 t。结构截面信息如图6所示,图6(a)为1~5层柱截面,图6(b)为6~15层柱截面,图6(c)为梁截面。采用拟力法对该结构进行动力非线性时程分析,地震波选用El-Centro波,峰值加速度调幅至6 m/s2。地震波施加到x方向,不考虑阻尼。有限元分析时,采用纤维梁单元,每个构件划分3个单元,整个结构共有2790个单元,13320个结点位移自由度,16740个塑性自由度。
4.2 时间复杂度比较
通过对上述结构进行非线性时程分析,得到该结构每个非线性步产生的塑性自由度数的曲线,如图7所示。可以看出,产生的最大塑性自由度数为d1=816,约为总位移自由数目的6.13%,并且达到最大塑性自由度数的计算步仅有1步。整个时程内产生的塑性自由度数在d2=200以下的概率较大,产生的平均塑性自由度数约为d3=53,约占总位移自由度数的0.4%。时程分析共有3000个计算步,仅有877步进入非线性阶段,约占总计算步的30%。对于本算例,产生塑性自由度数的理论最大值dmax≈1290。可见,实际产生的最大塑性自由度数d1 利用3.5节中传统变刚度法和拟力法的时间复杂度函数,结合本算例的模型数据信息,可得拟力法每步的时间复杂度,如图8所示。将两种方法的时间复杂度做对比,结果列入表3。产生的塑性自由度数分别取最大值d1=816,出现概率较大值d2=200,平均值d3=53三个代表值。 图4γmax随结构位移自由度数变化图 Fig.4 Change ofγmaxalong with the structural displacement degrees of freedom 图5 钢框架结构 Fig.5 Steel frame structure 图6 截面信息 Fig.6 Cross section information 从表3和图8可以看出,当产生的塑性自由度为最大值d1时,拟力法的时间复杂度达到最大值,约为1.95×108,远远高于其余计算步,整个时程的时间复杂度平均值约为1.46×107。传统变刚度法每步的时间复杂度约为7.41×108,拟力法的平均时间复杂度仅为传统方法的2%。 表3 两种方法的时间复杂度对比 Tab.3 Comparison of the time complexity of the two methods 修正自由度数d时间复杂度传统变刚度法13320100%7.41×108100%8166.13%1.95×10826.4%拟力法2001.50%1.51×1072.04%530.4%1.23×1071.70%注:表中每列数据的第二栏表示拟力法与传统变刚度法的比值。 综上所述,结构非线性分析时拟力法的时间复杂度要远远低于传统变刚度法。其中,产生的塑性自由度数大小与结构形式和地震强度有关。在不同情况下,结构进入塑性的区域大小要与本算例的结果有所区别,但一般情况下较小。 图9给出了拟力法每步的计算时间和平均值,两种方法计算时间的对比列入表4。 从图9和表4可以看出,当产生的塑性自由度数达到最大值d1时,拟力法的计算时间达到最大值0.058 s,整个时程的平均计算时间为0.025 s,而传统变刚度法的计算时间为0.158 s,拟力法的平均计算时间约为传统方法的15.8%。 表4 两种方法的计算时间对比 Tab.4 Comparison of time of the two methods 修正自由度数d计算时间/s传统变刚度法13320100%0.158100%8166.13%0.05836.7%拟力法2001.50%0.04025.3%530.4%0.03723.4%注:表中每列数据的第二栏表示拟力法与传统变刚度法的比值。 图7 塑性自由度 Fig.7 Plastic degrees of freedom 图8 拟力法的时间复杂度 Fig.8 Time complexity of FAM 图9 拟力法的计算时间 Fig.9 Time of FAM 由4.2节和4.3节可知,拟力法的时间复杂度和计算时间都远远小于传统变刚度法。但是两者的影响规律略有不同,有2个原因,(1) 时间复杂度计算时只考虑求解结点位移的计算量,忽略刚度矩阵合成等次要部分的计算量。并且假定乘除法与加减法耗时相同,但在实际计算机中两者的计算时间有差别。(2) 本文分析的基本操作只包括四则运算,而运行程序时还包括数据初始化、赋值和读写等操作。尤其当读写量较大时,该过程的耗时占很大比例。 本文利用算法复杂度理论分析了拟力法和传统变刚度法求解结点位移时的时间复杂度,给出了两种方法在一个非线性迭代步中的时间复杂度函数,并定量评价了二者的计算效率。结果表明,拟力法和传统变刚度法均为多项式算法。当结构进入非线性的区域较小时,传统方法的复杂度约为拟力法的m倍(m为刚度矩阵的带宽);当产生的塑性自由度数目达到理论最大值时,拟力法的复杂度将超过传统方法。算例表明,在非线性分析的过程中,结构进入非线性的迭代步较少,每步达到理论最大塑性自由度数目的概率较小,此时拟力法的时间复杂度更低,计算效率更高。 参考文献(References): [1] Bazaraa M S,Jarvis J J,Sherali H D.LinearProgrammingandNetworkFlows(ForthEdition)[M].Wiley,2009. [2] 韩忠明,陈 妮,乐嘉锦,等.面向热点话题时间序列的有效聚类算法研究[J].计算机学报,2012,35(11):2337-2347.(HAN Zhong-ming,CHEN Ni,LE Jia-jin,et al.An efficient clustering algorithm for time series of hot topics[J].ChineseJournalofComputers,2012,35(11):2337-2347.(in Chinese)) [3] 李 伟,徐志伟,卜冠英,等.网格环境下一种有效的资源查找方法[J].计算机学报,2003,26(11):1546-1549.(LI Wei,XU Zhi-wei,BU Guan-ying,et al.An effective resource locating algorithm in grid environments[J].ChineseJournalofComputers,2003,26(11):1546-1549.(in Chinese)) [4] 杨志军,陈 新,吴晓明,等.结构拓扑修改静态重分析自适应迭代方法[J].工程力学,2009,26(11):36-40,67.(YANG Zhi-jun,CHEN Xin,WU Xiao -ming,et al.An adaptive iteration method for structural sta-tic reanalysis of topological modifications[J].EngineeringMechanics,2009,26(11):36-40,67.(in Chinese)) [5] Deng L,Ghosn M.Pseudoforce method for nonlinear analysis and reanalysis of structural systems[J].JournalofStructuralEngineering,2001,127(5):570-578. [6] 梁晓雯.OFDM系统中自适应分配算法及其计算量的研究[D].中国科学技术大学,2006.(LIANG Xiao -wen.Adaptive Allocation Algorithms and Their Computational Complexity in OFDM System[D].University of Science and Technology of China,2006.(in Chinese)) [7] 胡景晨,王天舒.一种O(n)算法复杂度的递推绝对节点坐标法研究[J].力学学报,2016,48(5):1172-1183.(HU Jing-chen,WANG Tian-shu.A recursive absolute nodal coordinate formulation withO(n) algorithm complexity[J].ChineseJournalofTheoreticalandAppliedMechanics,2016,48(5):1172-1183.(in Chinese)) [8] Zhao P Y,Wu C,Litva J.Improved computational efficiency for the FDTD method[J].MicrowaveandOpticalTechnologyLetters,1994,7(2):60-62. [9] Sharif S,Yusoff W N S W,Omar Z,et al.Computational efficiency of generalized variance and vector variance[A].American Institute of Physics [C].2014. [10] Lin T H.TheoryofInelasticStructures[M].New York:John Wiley & Sons,Inc.,1968. [11] Wong K K F,Yang R.Inelastic dynamic response of structures using force analogy method[J].JournalofEngineeringMechanics,1999,125(10):1190-1199. [12] Wong K K F,Yang R.Earthquake response and energy evalution of inelastic structures[J].JournalofEngineeringMechanics,2002,128(3):308-317. [13] Wong K K F,Wang Y.Energy-based design of structures using modified force analogy method[J].TheStructuralDesignofTallandSpecialBuildings,2003,12(5):393-407. [14] Wong K K F,Zhao D.Uncoupling of potential energy in nonlinear seismic analysis of framed structures[J].JournalofEngineeringMechanics,2007,133(10):1061-1071. [15] Zhang X,Wong K K F,Wang Y.Performance assessment of moment resisting frames during earthquakes based on the force analogy method[J].EngineeringStructures,2007,29(10):2792-2802. [16] 李 钢,李宏男,李 灜.基于拟力法的消能减震结构地震反应分析[J].土木工程学报,2009,42(4):55-63.(LI Gang,LI Hong-nan,LI Ying.Analysis of seismic response of structures with dissipation devices by using fictitious force method[J].ChinaCivilEngineeringJournal,2009,42(4):55-63.(in Chinese)) [17] Li G,Li H N.Seismic response analysis of structure with energy dissipation devices using force analogy method[J].TheStructuralDesignofTallandSpecialBuildings,2011,20(3):291-313. [18] 李 钢,刘啟凤,李宏男.基于拟力法的MBC非线性控制[J].振动工程学报,2010,23(3):324-332.(LI Gang,LIU Qi-feng,LI Hong-nan.MBC nonlinear control strategy based on force analogy method[J].JournalofVibrationEngineering,2010,23(3):324-332.(in Chinese)) [19] 李 钢,余丁浩,李宏男.基于拟力法的纤维梁有限元非线性分析方法[J].建筑结构学报,2016,37(9):61-68.(LI Gang,YU Ding-hao,LI Hong-nan.Nonlinear fiber beam element analysis based on force analogy method[J].JournalofBuildingStructures,2016,37(9):61-68.(in Chinese)) [20] Li G,Zhang Y,Li H N.Nonlinear seismic analysis of reinforced concrete frames using the force analogy method[J].EarthquakeEngineering&StructuralDynamics,2014,43(14):2115-2134. [21] 王晓东.计算机算法设计与分析(第3版)[M].北京:电子工业出版社,2007.(WANG Xiao -dong.TheDesignandAnalysisofComputerAlgorithms(ThirdEdition)[M].Beijing:Publishing House of Electro -nics Industry,2007.(in Chinese)) [22] 郑勋烨.计算方法及MATLAB实现[M].北京:国防工业出版社,2015.(ZHEN Xun-ye.CalculationMethodandMATLABImplementation[M].Beijing:National Defense Industry Press,2015.(in Chinese)) [23] 徐树方,高 立,张平文.数值线性代数(第2版)[M].北京:北京大学出版社,2013.(XU Shu-fang,GAO Li,ZHANG Ping-wen.NumericalLinearAlgebra(SecondEdition)[M].Beijing:Peking University Press,2013.(in Chinese)) [24] Golub G H,Van Loan C F.MatrixComputations(ForthEdition)[M].Baltimore:The Johns Hopkins University Press,2014. [25] 维 斯.数据结构与算法分析——C++描述(第3版)[M].人民邮电出版社,2012.(Weiss M A.DataStructuresandAlgorithmanalysisinC++(ThirdEdition)[M].Beijing:Posts & Telecom Press,2012.(in Chinese)) [26] Hager W W.Updating the inverse of a matrix[J].SIAMReview,1989,31(2):221-239. [27] Burden R L,Faires J D.数值分析(第七版)[M].北京:高等教育出版社,2005.(Burden R L,Faires J D.NumericalAnalysis(SeventhEdition)[M].Beijing:Higher Education Press,2005.(in Chinese)) [28] Kirsch U.ReanalysisofStructures:AUnifiedApproachforLinear,Nonlinear,StaticandDynamicSystems[M].Springer,2008.


4.3 计算时间比较




5 结 论

