基于差值法的荷载试验分析研究
胡惠康,元 萌
(1.上海中测行工程检测咨询有限公司,上海市 200438;2.上海岩土工程勘察设计研究院有限公司,上海市 200438)
0 引言
桥梁荷载试验即通过对桥梁结构直接加载后进行有关测试、记录与分析工作,以了解桥梁结构在试验荷载作用下的实际工作状态,进而评定桥梁结构施工质量和使用状况,为竣工验收和桥梁检测提供科学依据[1]。
在以往对钢便桥(包括部分钢桁架桥梁)的荷载试验中可以发现,结构在各级荷载的作用下,其实测的挠度值往往都会大于有限元模型计算的理论值,控制截面测试的应变值也与理论值十分不符[2]。钢便桥由众多贝雷梁拼装而成,而预制的贝雷梁虽然采用相同的尺寸规格,但是其制作误差和施工误差可能使结构存在较大的局部受力(或局部不受力),而销接的拼装方式使得结构连接不紧密[3],加剧了结构的局部受力和变形异常状况,这种现象并非静载试验中的预压可以消除。造成的结果便是结构控制断面的实测应变和挠度值都与理论值存在较大差异,这种数据的不准确性导致了对桥梁结构实际承载能力的不合理判断。
因此为了解决上述问题,需要一种新的静载试验分析方法。下面以浦东机场钢便桥荷载试验为例,进行详细阐述。
1 工程概况
为满足浦东机场扩建需要,需在南随塘河上新建一座钢便桥。该桥选型为“321型”成品组合式钢桥,选用的组合型式为三排单层加强型钢便桥,材料为16M n钢。新建钢便桥长48 m,宽5.85 m,桥面板净宽4 m,为双向单车道。钢便桥整体由横梁、桥面板、加强弦杆、横梁夹具、水平支撑架、竖向支撑架、联板等组成。设计载重为80 t。浦东机场钢便桥立面照和平面照分别如图1和图2所示。

图1 浦东机场钢便桥立面照

图2 浦东机场钢便桥平面照
2 荷载试验方案
2.1 测点布置
该次静力荷载试验选取第一跨和第二跨作为观测对象。主要观测在最不利荷载工况下,第一跨与第二跨跨中最大挠度、上下弦杆贝雷梁最大拉压应力及斜腹杆最大拉压应力,以及横向分配梁跨中梁底应变及挠度。测点布置见表1和图3,桥台、桥墩及支座沉降测点布置由于篇幅有限,不做介绍。图3中除C-1#测点布置于横梁中间外,其余测点均布置在西侧最内测一排的钢构件上。

表1 应变及挠度测点布置表

图3 应变及挠度测点纵断面布置图(单位:mm)
2.2 加载工况及车辆布载
根据试验要求,该次荷载试验以80 t荷载为标准荷载,为方便分级加载,现场采用4辆三轴重车作为加载车,载重分别为 20 t、40 t、60 t和 80 t;加载车前中轴距1.4m,中后轴距4.6m,轮距1.9m。该次试验共分五工况加载,每个工况分四级加载,由于桥面较窄,该次试验仅需考虑中载状况。车辆布置位置如图4和图5所示,车头均朝南,每个工况在图4所示对应的加载位置采用上述四种不同重量的车辆来模拟四级加载。
在加载过程中,应对各测点的应变、挠度及沉降均进行观测,但每级加载需要控制不同的主要参数,分别为:
(1)加载工况一。第一跨贝雷梁跨中挠度及跨中截面上、下弦杆的应变。
(2)加载工况二。第一跨跨中横向分配梁中间处应变。
(3)加载工况三。第一跨贝雷梁桥墩立柱附近斜腹杆的拉、压应变。
(4)加载工况四。第二跨贝雷梁墩顶立柱附近斜腹杆的压应变。
(5)加载工况五。第二跨贝雷梁跨中挠度。
3 静载试验结果与分析
按照上述五个工况进行加载后,将所得的应变及挠度数据与模型理论值进行对比分析,该桥的理论值从M ID A S/Civil有限元模型中得到,模型如图6所示。模型中钢桁架均采用梁单元模拟,桥面板采用板单元模拟,各钢桁架杆件间采用释放梁端弯矩方式来模拟销接。

图6 浦东机场钢便桥有限元模型
在各工况荷载作用下,主要测试截面的实测应变值与理论应变值见表2,表中应变数值均已考虑残余应变影响。在各工况荷载作用下,主要测试截面的实测挠度值与理论挠度值见表3,表中挠度实测值均已考虑结构沉降和残余挠度的影响。
由表2可知,工况一的测点A-1和工况三的测点B-1的应变校验系数大于1,不满足《公路桥梁荷载试验规程》(JTG/T J21-01—2015)的要求;由表3可知,三个挠度测点的校验系数均远大于1,不满足规范要求。
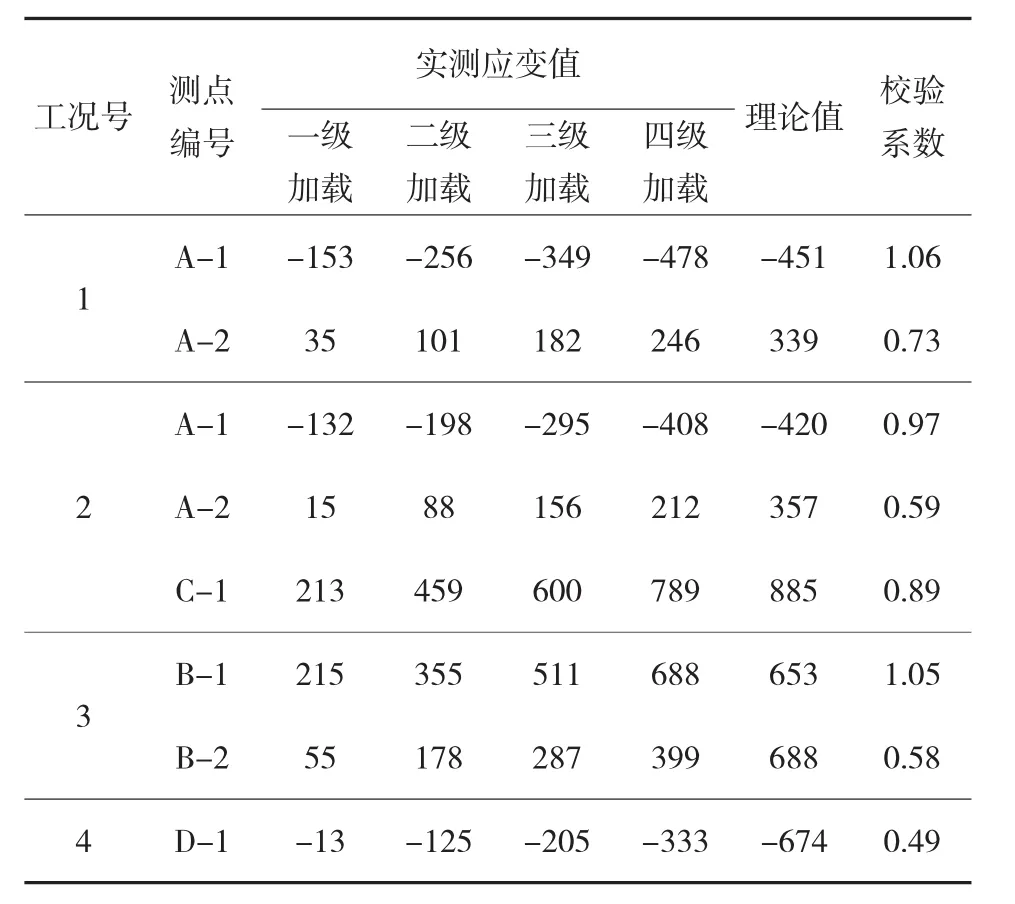
表2 各应变测点实测值与理论值比较 με

表3 各挠度测点实测值与理论值比较 mm
4 差值荷载试验分析法
为了测试该钢便桥的真实承载能力,该试验采用60 t的三轴重车,分三级加载,再次进行荷载试验,测试结果与80 t荷载类似,依然无法满足规范要求。为了分析原因,对上述80 t荷载试验结果进行分析,分析结果如图7~图9所示。
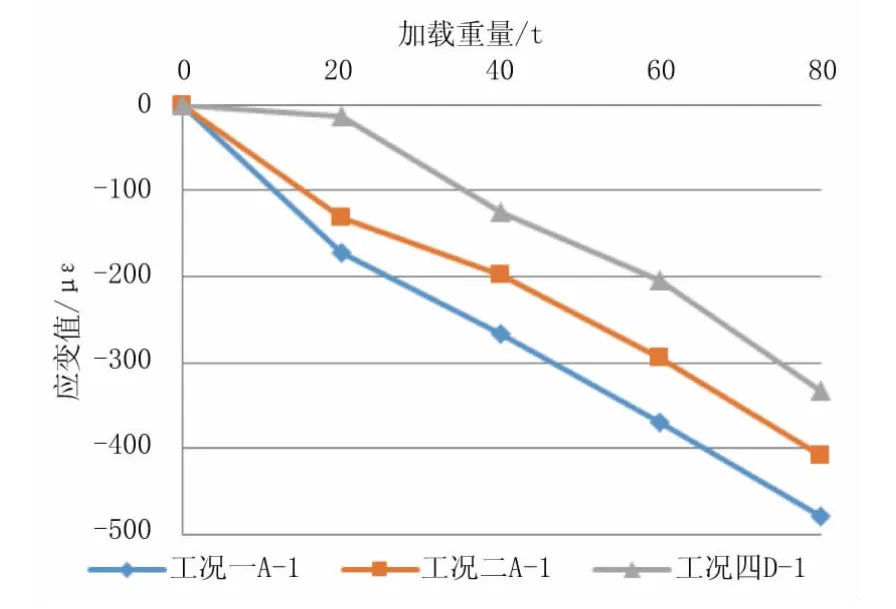
图7 各级荷载作用下各测点的应变值(一)
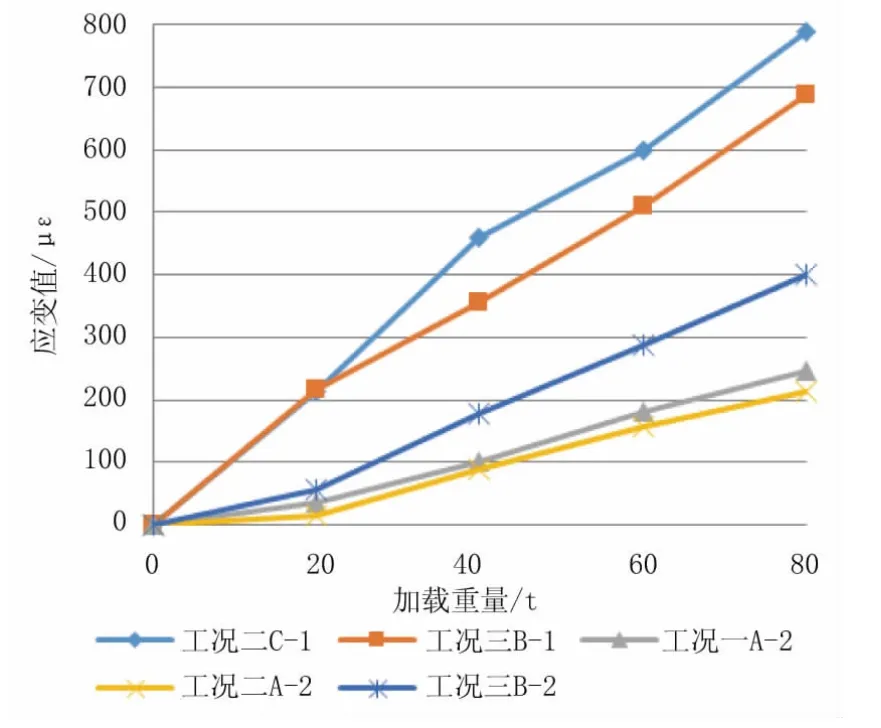
图8 各级荷载作用下各测点的应变值(二)

图9 各级荷载作用下各测点的挠度值
由图7和图8可知,除了工况二C-1和工况三B-1测点的应变值大致呈一条直线外,其余测点应变值均存在较大拐角,而在图9的挠度值中更为显著。出现这种状况的原因为所有测点数值连线中,在0 t和20 t处数值连线的斜率与20~80 t处数值连线斜率相差较大。在钢结构试验中得到这样的结果是不正常的。
其主要原因为:钢便桥销接处连接不紧密,导致在较小荷载的作用下,整体结构无法进入工作状态,而且会产生很大的变形,构件的预制尺寸误差和施工误差会造成部分构件在小荷载作用下不受力,造成应力分布不合理。当结构进入整体工作状态时,这种影响会大大降低。
上述原因造成钢便桥荷载试验数据的不准确,为了消除这种不准确性,本文提出差值荷载试验分析法。
所有的试验数据均由试验真值和误差构成,即试验数据=试验真值+试验误差。每增加一级荷载都会增加一个真值和一个误差,每个工况的试验数据可以描述如下:
一级加载:数据1=真值1+误差1。
二级加载:数据2=数据1+真值2+误差2。
三级加载:数据3=数据2+真值3+误差3。
四级加载:数据4=数据3+真值4+误差4。
一级加载的荷载为20 t,可以确保此时的结构完全进入工作状态(即所有构件均开始受力,不存在局部不受力状态),且已消除结构连接不紧密状态。即误差1已经包括了结构局部不受力和连接不紧密的大部分影响。因此在整个试验中,只要能消除误差1的影响,即可得到较为真实的试验数据。现对上述数据做以下处理:
单级差值1=数据2-数据1=真值2+误差2
单级差值2=数据3-数据2=真值3+误差3
单级差值3=数据4-数据3=真值4+误差4
总差值1=数据2-数据1=真值2+误差2
总差值2=数据3-数据1=真值2+真值3+误差2+误差3
总差值3=数据4-数据1=真值2+真值3+真值4+误差2+误差3+误差4
在上述六个差值中,均不存在误差1的影响,可以得到较为真实的数据。将此方法应用于钢便桥试验,可以得到表4和表5的结果。
由表4和表5可知,各应变单级差值的校验系数为0.48~1.13,有少数几个测点超过1.00,但是超幅不大;各应变总差值的校验系数为0.58~1.13,其中总差值3的校验系数为0.64~0.97,小于1。各挠度单级差值的校验系数为0.68~1.08,仅一个测点校验系数大于1,且超幅不大;各挠度总差值的校验系数为0.88~1.08,其中总差值3的校验系数为 0.88~0.93,小于 1。

表4 各应变实测差值与理论差值比较 με

表5 各挠度实测差值与理论差值比较 mm
通过差值法消除结构局部不受力和连接不紧密的影响后,可以得到如下结论:在各级荷载作用下,各应变和挠度单级差值校验系数较为合理,应变总差值3和挠度总差值3的校验系数均小于1,表明结构在20~80 t的荷载增量作用下,其实际应变和挠度增量均小于理论应变和挠度增量。
5 结语
(1)差值法可以有效消除钢便桥构件连接不紧密和尺寸误差的影响,使荷载试验能精确评价钢便桥的实际承载能力。
(2)当采用差值法分析荷载试验时,建议加密对荷载的分级。当荷载分4~6级加载时,第一级加载的荷载值不宜过小,确保结构完全进入工作状态;当荷载分级大于6级时,可在第二级加载时结构完全进入工作状态,需结合实际情况判断。
(3)对连接松散或尺寸误差较大的结构进行荷载试验时,可能存在部分构件在结构完全进入工作状态前已承受较大的应力,因此试验人员需要在试验过程中对结构主要受力构件的总应力进行控制,确保其处于结构的极限承载范围内。
(4)差值荷载试验法中的单级差值法较为严格,若单级差值法或总差值法前几级存在校验系数大于1(超幅不应过大),但总差值法最后一级的校验系数小于1,也可判定结构承载能力满足要求。
(5)结构连接不紧密的影响在荷载试验中可通过差值法修正,但进行技术状况评定时应作为结构缺损进行考虑,其紧密程度可参考荷载试验各工况的前几级加载结果进行评判。
(6)基于差值法的荷载试验分析对连接松散或在小荷载作用下存在较大误差的结构均可适用。
参考文献:
[1]谌润水,胡钊芳.公路桥梁荷载试验[M].北京:人民交通出版社,2003.
[2]袁红茵,戴永相,张文杰.贝雷架钢桥的静动力荷载试验的研究[J].桥涵工程,2007(5):84-87.
[3]黄文,袁向荣.钢便桥静动载试验研究[J].长春工程学院学报:自然科学版,2010,11(4):27-29.

