金沙江乌东德水电站工程中三角高程测量代替二等水准测量的可行性研究

杜正乔,杜俊凤

(长江三峡技术经济发展有限公司乌东德水电站建设部,昆明 651500)

1 工程概况

乌东德水电站位于四川省会东县和云南省禄劝县交界的金沙江河道上，是金沙江水电基地下游河段4个水电梯级中的第1梯级，为Ⅰ等大(1)型工程。乌东德水电站海拔落差大，两岸地势高，地形复杂，开挖难度大，为了给电站地下机组安装提供精确、可靠的高程基准，需将电站地下主厂房已知水准点导入至机窝待测水准点。

为满足规范[1]要求，高程控制网要达到二等及以上水准测量的精度，需利用精度高的水准仪及铟瓦尺进行测量。这种传统测量方法在地形平坦、交通便利的地区，操作简单、精度高，但是从地下厂房已知水准点至机窝待测水准点高差大，水准路线长，施工环境复杂，用传统方法测量难以满足要求。三角高程测量具有现场观测简单、灵活、受现场环境限制较小等优势，尤其近年来科学技术的发展，高精度全站仪的不断涌现，利用全站仪代替水准测量成为可能。因此，研究基于智能全站仪的高精度水准测量，以弥补传统水准测量的不足，提高作业效率和降低劳动强度，具有重要的意义[2]。

2 全站仪测量高程原理

2.1 单向测量高程的原理

利用全站仪测量任意两点之间距离和天顶距来求两点间高差的方法，称为三角高程测量[1]。如图1所示，A为已知点，B为待测点，将全站仪架设于A点置平，量取仪器高iA，将反光镜架设B点，量取棱镜高vB，可推导A、B两点间的高差计算公式为：

hAB=SAB·sinαAB+iA-vB+c-r

(1)

式中：hAB为A、B两点的高差;SAB为A、B两点间的斜距;αAB为A至B的天顶距；c为地球曲率；r为大气折光系数。可知c、r的计算公式为[3]：

(2)

(3)

式中：kAB为A至B方向的大气折光系数；R为地球平均曲率半径，SAB、DAB分别为仪器到棱镜的斜距和平距。

因此，全站仪单向三角高程测量的计算公式为：

(4)

图1 全站仪测量原理示意图

2.2 对向测量高程的原理

对向测量又称为往返测量，其原理与单向测量相同。将全站仪架设A点，棱镜于B点，测得A、B两点间的高差hAB为往测高差；再将全站仪架设B点，棱镜于A点，测得B、A两点间的高差hBA为返测高差。往返测量高差的平均值作为最终测量结果[4]。

根据式(4)可得往返测计算公式。

往测计算公式:

(5)

返测计算公式:

(6)

可求对向高差的公式为：

(7)

由此可以看出，在气象稳定的条件下，全站仪测量可不考虑地球曲率及大气折光系数对高程测量精度的影响。

3 乌东德水电站工程中的可行性分析

为验证对向三角高程测量能代替二等水准测量的可行性，选取水电站地下主厂房观测标墩Y-ZCF、机蜗隔墩地面水准点JW2个点，分别进行对向测量。

3.1 二等水准测量

3.1.1 水准路线及测量步骤

(1) 测量仪器：徕卡DNA03电子水准仪，测距精度(±0.6+1×10-6L) mm，配套设施为铟瓦条码尺、尺垫、卷尺或钢卷尺等。

(2) 水准路线：经过现场踏勘，选取一条合适的水准路线(见图2)。往测从主厂房安装间埋设的二等水准强制观测墩Y-ZCF点开始，沿主厂房安装间→进厂交通洞→右厂4号施工支洞→10号引水隧洞→高程789.70 m机组隔墙平台→二等水准点JW；返测与往测线路相反。

图2 右岸地下主厂房Y-ZCF至JW二等水准测量路线图

(3) 观测次序：根据二等水准测量的技术要求，严格按照DL/5173-2012《水电水利工程施工测量规范》执行[5]。

(4) 按照观测顺序，逐站测量，由Y-ZCF至JW，再由JW至Y-ZCF。

3.1.2 水准测量实测数据

在设站前先用皮尺丈量前后视距离，观测应在标尺成像清晰、铟瓦水准尺稳定时进行。水准记录采用仪器自动记录，当天数据当天下载保存，并对数据校核[6]。平差计算成果见表1。

表1 二等水准测量数据成果表

3.2 对向高程测量

3.2.1 仪器设备及测量步骤

(1) 测量仪器：徕卡TM30全站仪,测角0.5″、测距精度(±0.6+1×10-6L) mm，配套设备有棱镜、三脚架、钢板尺、对讲机等[7]。

(2) 在强制观测墩Y-ZCF点上安置全站仪，量取仪器高并记录；在高程789.70 m平台上埋设的水准点JW上安置棱镜，量取棱镜高并记录。

(3) 可在全站仪上输入各项改正参数后，直接读取高差或使用天顶距计算高差，观测时全站仪按照盘左、盘右分别进行观测记录，观测数严格按照规范中的要求(见图3)[3]。

(4) 往测观测结束后，返测将全站仪、棱镜交换位置架设，在高程789.70 m平台上埋设的水准点JW上安置的三脚架不动，安置完成后量取仪器、棱镜高并记录，按往测步骤进行操作并记录。

图3 全站仪对向三角高程测量示意图

3.2.2 对向实测数据

对向三角高程测量数据见表2。

表2 对向三角高程测量数据表

3.3 测量成果对比

经计算二等水准测量高差和三角高程测量高差如下。

二等水准测量高差：

三角高程测量高差：

h三角高程=-35.1199 m

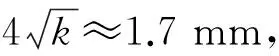
4 测量精度分析

4.1 中误差公式推导

依据测量误差的传播定律，对式(7)进行微分，并转换为中误差关系式，则式(7)可推导为[9]：

(8)

式中：mh为对向测量的平均高差中误差;mSAB、mSBA、mαAB、mαBA为往返斜距和天顶距中误差;miAB、mvAB、miBA、mvBA为往返仪器高和棱镜高中误差。由于仪器的观测条件相同，则mSAB=mSBA=mS，mαAB=mαBA=mα，SAB=SBA=S,miAB=mvAB=miBA=mvBA=m，αAB=αBA=α，于是式(8)可简化为：

(9)

对式(9)进行开平方，则：

(10)

由式(10)可知，误差来源主要有测角误差、测距误差及仪器高和棱镜高量取误差。

4.2 各项误差分析

4.2.1 TM30全站仪

徕卡TM30是瑞士仪器公司生产的一款高精度智能全站仪，具有独特的智能目标识别技术，在极高转速的情况下，也能具备极高的测量精度和更远的测量距离，同时会自动识别和锁定目标，不妨碍其他光源的干涉，能进行正常跟踪测量[10]。

4.2.2 测角和测距精度

采用测回数为n次,并取2倍的测角、测距误差为极限值。

测角中误差为：

(11)

测距中误差为：

(12)

4.2.3 仪器高和棱镜高的量取方法

从计算公式中可知需量取仪器高和棱镜高，而传统的量取方法是用钢卷尺从水准点量至架于三脚架上仪器或棱镜的中心位置的距离，但其量取的距离为斜距，而非水准点至仪器或棱镜的垂直距离，其精度一般在1～2 mm，不能满足精密三角高程测量的规范要求[11]。

利用全站仪间接量取置于水准点上方的棱镜高度(如图1)，A为置于水准点S上的棱镜，a为置于水准点S上的小棱镜，其棱镜高HSa已知，在自由测站点B架设全站仪，分别测量棱镜A和a的天顶距、斜距观测值。

依据三角测量高程的原理，推导出A、B两点间的高差为：

hAB=S·sinα+i-v

(13)

则得B、A和B、a之间的高差分别为：

hBA=SBA·sinαBA+iB

(14)

hBa=SBa·sinαBa+iB

(15)

由式(14)～式(15)可得棱镜a与A之间的高差：

haA=hBA-hBa=SBA·sinαBA-SBa·sinαBa

(16)

其水准点S上的棱镜高HSa已知，可得棱镜A至水准点S的高差为：

hSA=HSA+haA=HSa+SBA·sinαBA-SBa·sinαBa

(17)

对式(17)进行全微分计算并运用协方差传播定律，得高差hSA的测量中误差为：

(18)

现假设αBA=0.15°，αBa=2.00°，SBA≈SBa=40 m，ρ=206 265，仪器精度为:0.5″,(0.6+1×10-6L) mm,代入式(18)得：mhSA=0.02 mm。考虑现场实际情况不同，仪器架设场地不平整，αBA、αBa、SBA、SBa与假设情况差距较大，但仪器需尽可能地架设在与棱镜同一水平面，并多次测量取平均值，进一步提高其精度，则仪器高和棱镜高的量取误差可控制在0.01～0.04 mm之间。

4.2.4 极限误差

为了验证对向三角高程测量能代替二等水准测量的可行性，列表计算当天顶距<15°时，在不同边长的对向高差中误差,同时取2倍的测角、测距误差为极限误差(见表3)。观测测回数n=4，仪器高和棱镜高的量取误差取mi=mv=±0.03 mm[12]。

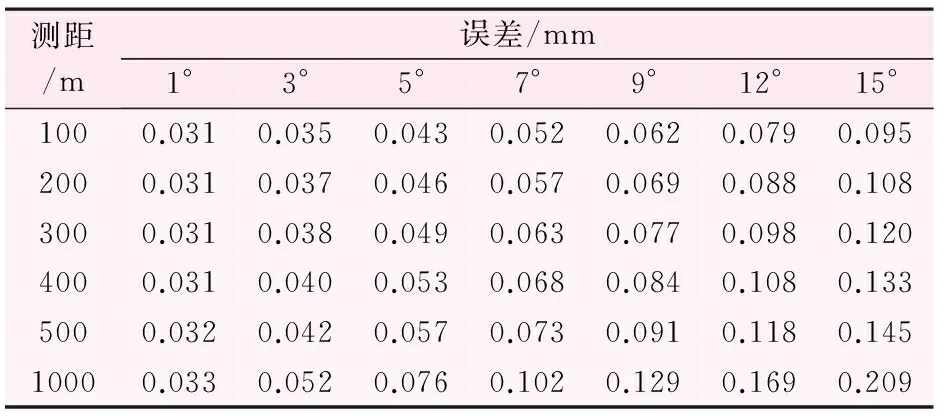
表3 全站仪三角高程测量的极限误差表

5 结 语

根据上述分析，得出以下结论：

(1) 用对向三角高程测量方法代替水准测量，操作简单方便、受地形影响小。较传统水准测量方法，对向三角高程测量速度快、效率高、减小了劳动强度。

(2) 因大气折光系数k受外界环境和高程变化而变化，观测视线方向的大气折光系数很难确定，由计算公式(7)可知，在气象稳定的条件下，全站仪测量可不考虑地球曲率及大气折光系数对高程测量精度的影响，从而提高了测量精度[13]。

(3) 对观测受仪器的测角、测距精度影响较大时，为达到测量的精度要求，测量时应选用高精度仪器。

(4) 应多次测量取平均值，以提高测量精度。

(5) 由表3可知，高差中误差，随测角、测距的增大而增加，但测角对高差中误差的影响要大于测距对高差中误差的影响，所以在进行对向三角高程观测测量时，应尽量减小测角与测距，以提高测量精度。

参考文献:

[1] 国家质量技术监督局.国家三角测量规范:GB/T 17942-2000[S].北京：中国质检出版社，2014.

[2] 徐福国.TCA2003全站仪在拉西瓦水电站工程中的应用[J].科技创新导报,2012(16)：51-53.

[3] 黄兆铭,张智韬.全站仪三角高程测量误差与边长及角度的关系[J].科技资讯,2009(07):50-51.

[4] 任东风,马超.全站仪三角高程测量方法与精度分析 [J].测绘与空间地理信息,2017(01):13-17.

[5] 国家能源局.水电水利工程施工测量规范:DL/T 5173-2012[S].北京：中国电力出版社，2016.

[6] 国家标准化管理委员会.国家一、二等水准测量规范:GB/T 12897-2006[S].北京：中国标准出版社，2006.

[7] 杨凤芸,赵文,刘玉梅.TM30三角高程代替二等水准测量的精度分析[J].沈阳建筑大学学报(自然科学版),2012(04):657-662.

[8] 张江,马文静.基于智能全站仪精密三角高程测量方法研究 [J].铁道勘察 ,2011(06):9-11.

[9] 张智韬,黄兆铭,杨江涛.全站仪三角高程测量方法及精度分析[J].西北农林科技大学学报(自然科学版),2008(09):229-234.

[10] 周青青,邱本立.全站仪不同方法施测三角高程测量的精度分析[J].科技信息,2011(23):47-48.

[11] 王春青,李瑶,李霞.基于智能型全站仪进行精密三角高程测量的理论探讨及实践应用[J].青海国土经略,2014(02):75-77.

[12] 叶达忠,黎富忠.桂中治旱引水一期工程高精度水准网技术设计与实施[J].测绘通报,2012(S1):131-133.

[13] 杨凤芸.边坡高精度监测系统及变形趋势预测的研究[D].沈阳：东北大学,2012.