基于整数尺法角度的佛光寺东大殿营造用尺复原研究*

张毅捷 韩 效 丁 拓 马民政 雒国辉 郝正坤

ZHANG Yijie, HAN Xiao, DING Tuo, MA Minzheng, LUO Guohui, HAO Zhengkun

0 引 言

我国现存六栋唐代木构遗存①，其中以山西五台佛光寺东大殿（创建于公元857年）等级最高，保存最为完好，是建筑史以及建筑技术史的重要研究对象。而营造用尺尺长作为与建筑设计和建筑施工密切相关的物理量是建筑技术史研究的重要内容，同时，对古代建筑遗存营造用尺尺长的复原和丰富我国尺度史研究也有重要的意义和价值。

佛光寺东大殿作为唐代的殿堂建筑，原构保存最为完好，规模最大，一直都是建筑史界关注的焦点，从1937年梁思成等发现这栋建筑并对其进行了实测、考察和研究之后又陆续有几次比较重要的考察：雁北文物考察团的考察（1951）、山西省文物工作委员会的考察（1964）、中央及地方文物工作者的考察（1973）、山西省古建筑保护研究所的考察（2004）、清华大学的考察（2006）等，这些考察形成了几套实测成果：梁思成、陈明达、傅熹年、柴泽俊、山西古建筑保护研究所以及清华大学②，其中以清华大学的实测手法最先进，测量结果精度最高，也最为客观，本文将基于整数尺法的理论分析清华大学的测量数据。

1 本研究的理论背景

本研究的理论背景主要有三方面：整数尺法、尺度史以及作为木工道具的营造尺。

1.1 整数尺法

整数尺法最早源于日本近代建筑史研究，日文称“完数柱間制”。即日本学者在对奈良时代（八世纪左右）遗存建筑进行详细实测、复原研究时发现，“这一时期建筑平面开间的尺度构成，以整数尺值为最基本的原则”③。之后张十庆沿着这个思路分析了中国唐、辽、宋的部分遗存发现，这种现象也存在于中国早期建筑。例如根据张十庆的分析，佛光寺东大殿心间和两个次间均为17唐尺，尽间以及进深各间都是15唐尺，而折算出来的唐尺尺长约为29.6 cm（图1）④。也就是说中国早期建筑遗存（北宋迄前）的开间进深尺寸中存在着一种整数尺控制的现象，本文称其为“整数尺法”。本文将继续沿着整数尺法的思路对佛光寺东大殿的实测数据继续进行分析。

1.2 尺度史

大约四千年前，中国就开始有尺度的概念，此后历朝历代都十分重视制定尺度的规制，同时史籍中的相关记载和研究也比较丰富，而现代意义上最早涉及历代尺度厘定的研究是民国时期的吴承洛，1949年之后还有杨宽、郭正忠、丘光明等，目前有关尺度史，特别是唐代尺度史的研究比较成熟。早期的研究从钱币、城址和大小尺比例等角度对唐尺进行了复原，而丘光明也从现存唐尺实物出发对唐尺尺长进行了推测。

根据丘光明的统计现有存世唐尺40把，但这些唐尺实物尺长偏差很大，即便是以两把分寸刻度精确的白牙尺为准推测唐大尺为29.5 cm左右，也不能否认唐尺尺长有在30 cm之上的可能。例如这40把存世唐尺尺长29～29.99 cm的有15把，尺长30～30.99 cm的有13把，31 cm以上的有11把。基本上这些存世唐尺尺长在29～31.8 cm范围内⑤。

1.3 作为木工道具的营造尺

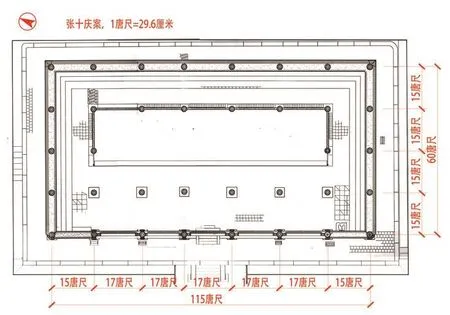
图1 佛光寺东大殿平面图·平面柱网设计推测方案一（张十庆案）Fig.1 Plan of Main Hall in Fogongsi Temple (Design Scheme Speculated by Shiqing Zhang)

建筑和尺度密切相关，这是因为建筑的设计和施工都离不开用尺，木工用尺在中国学界被称为营造用尺，是中国尺的三种尺系之一⑥。中国学界最早关注营造用尺的是吴承洛，在他30年代的专著《中国度量衡史》中描绘了民国时期营造用尺紊乱之现象，并指出这是由于营造用尺“为木工所用，推行较广，故尺寸之流传，自不能尽行一致”⑦，也就是说营造用尺作为应用广泛的尺虽然本于官尺，但是各地、各个木匠流派，甚至是每栋建筑中的营造用尺尺长略有差异是正常现象。因此从遗存实测尺寸出发复原营造尺是一种合理和可行的研究方法。

2 基于整数尺法的东大殿平面柱网尺寸分析

如前所述近代以来对佛光寺东大殿有数次实测调研，以清华大学2008年的勘察精度最高，本文准备从整数尺法的角度对清华大学此次实测的数据进行探讨。清华大学的研究表明，佛光寺东大殿的柱子存在侧脚和升起的做法，因此本次研究关注此次实测的柱头尺寸。东大殿平面柱网柱头实测尺寸如表1：

表1 佛光寺东大殿柱网柱头实测尺寸表Tab.1 table of real measurements of bay width(at the top of columns) of Main Hall in Fogongsi Temple (Unit: mm)

从实测数据可以看出，这栋面阔七间进深四间的庑殿建筑，正面中央五间尺度比较接近，一般认为这五间开间面阔一样，而进深四间的尺度也被认为是一样的，并且根据庑殿建筑的构造特点，这四个进深尺寸也分别与正面尽间的面阔尺寸一致。也就是说，这栋建筑的平面柱网柱头尺寸共四种尺度：尽间面阔（分间进深尺寸）、心间面阔、总面阔和总进深。根据上述实测尺寸求得这四个尺寸的均值分别为：尽间面阔（亦即分间进深尺寸）均值4 400.67 mm，心间面阔均值5 041.22 mm，总面阔均值33 979.45 mm，总进深均值17 610.71 mm。

根据张十庆的研究，该建筑中央五间的面阔都是17唐尺，尽间15唐尺，总面阔2×15+5×17＝115唐尺，总进深=4×15=60唐尺，唐尺尺长约29.6 cm（图1）。下面用唐尺尺长29～31.8 cm来处理上述四个均值如表2，表中是将总面阔尺寸以唐尺的约数29～31.8 cm来折算，取尺数为整数，再用此整数尺数的总面阔折算的尺长折算其他尺寸。

从上表可见，折算值c非常接近于张十庆的推测，而折算值j的各个折算尺寸在上述11套折算值中最接近于整数，因此该建筑在整数尺法的理论背景下还有可能是中央五间面阔都是16唐尺，尽间面阔及各个进深为14唐尺，总面阔2×14+5×16＝108唐尺，总进深4×14=56唐尺，此时1唐尺约为31 cm余⑧。下面分析比较这两套尺度（折算值c和折算值j）如表3：

该表第二行列出了前述四项实测数据的均值J，第三行和第十二行列出了张十庆和本研究的两组推测设计值S，而第4、6、8、10行则给出了分别根据四项实测尺寸均值J的推测设计值S1计算出来的折算尺寸Z1，第13、15、17、19行则是同样方法根据推测设计值S2计算出来的折算尺寸Z2，最后分别计算出了这些折算尺寸Z与实测值均值J之间的差值C。比较各个差值可以看出，整体以唐尺2为设计值的折算尺寸与实测均值尺寸更为接近，其中又以总面阔按设计推算值S2=108唐尺折算出来的折算尺寸与实测均值最为接近（最大C值为8.26 mm），因此初步判断，这栋建筑有可能是以推测设计值S2进行设计，而具体的唐尺尺长约为：唐尺2=33979.45÷108≈31.46 cm。为了进行对比这里也对唐尺1进行推测，1唐尺1=33979.45÷115≈29.55 cm。

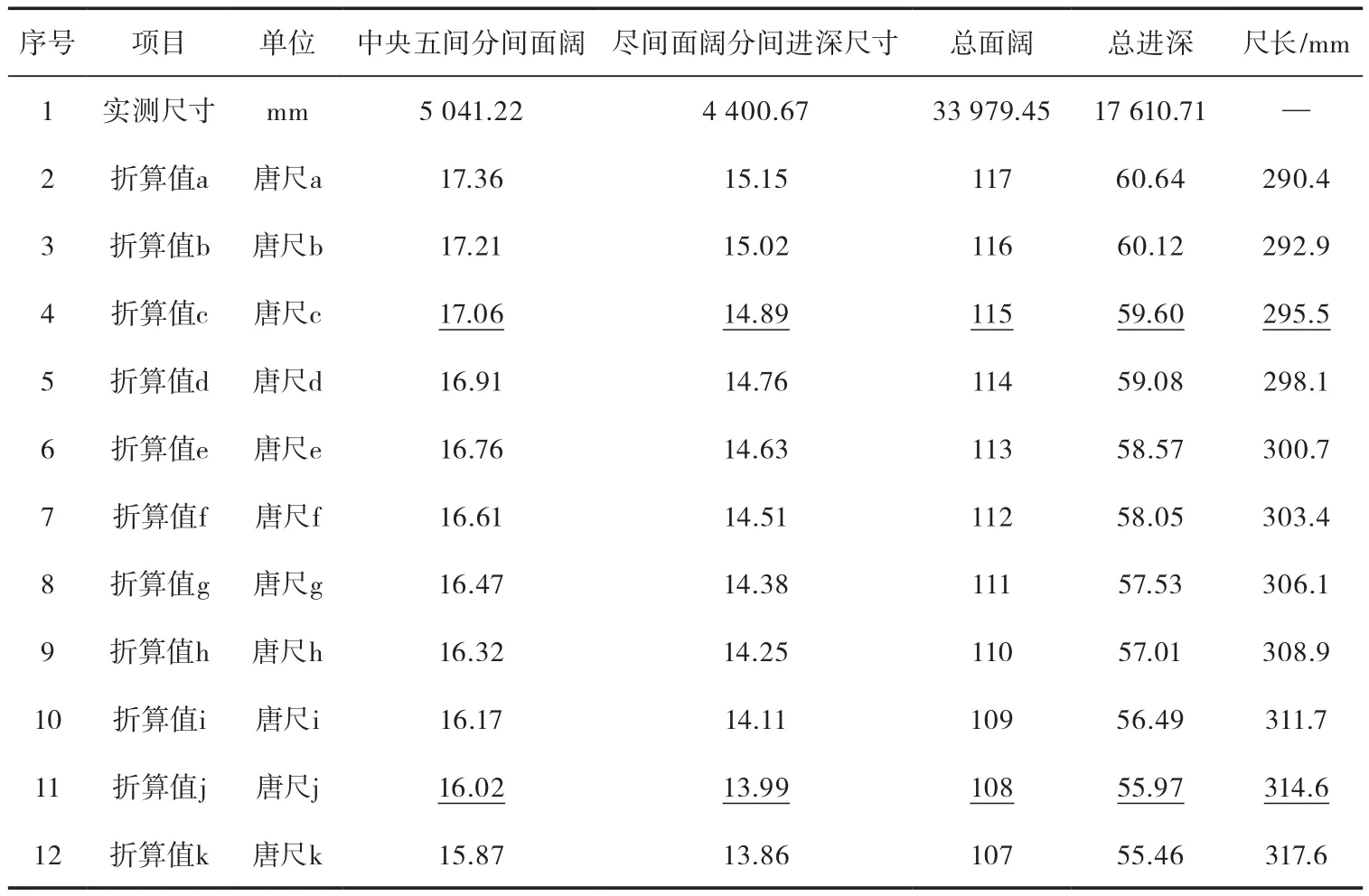
表2 佛光寺东大殿平面柱网尺寸分析表一Tab.2 analysis table A of measurement of bay width of Main Hall in Fogongsi Temple

表3 佛光寺东大殿平面柱网尺度分析表二Tab.3 analysis table B of measurement of bay width of Main Hall in Fogongsi Temple

表4 佛光寺东大殿柱高实测尺寸表Tab.4 table of real measurement of height of column in Main Hall in Fogongsi Temple (Unit: mm)

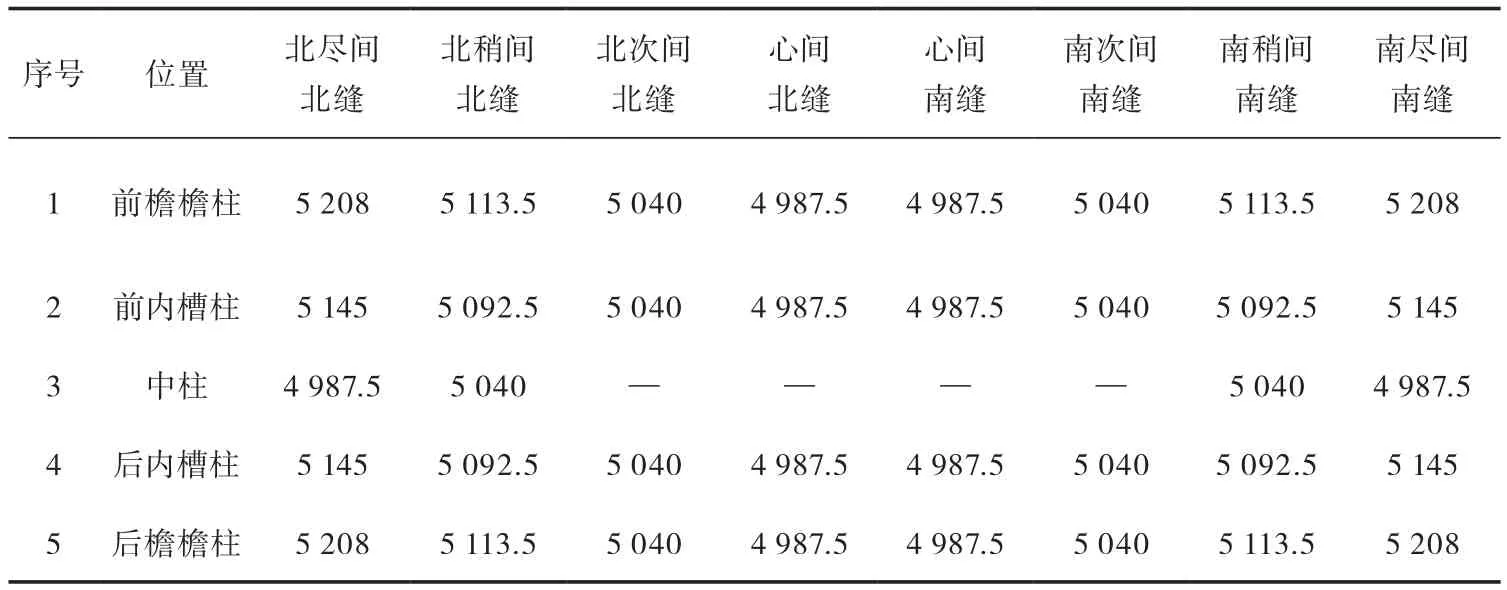
表5 佛光寺东大殿柱高尺寸复原表Tab.5 table of reconstructive measurement of height of column in Main Hall in Fogongsi Temple

表6 佛光寺东大殿柱高生起尺寸分析表Tab.6 analysis table of measurement of increase of height of column named shengqi in Chinese in Main Hall in Fogongsi Temple

以上是根据平面柱网柱头尺寸实测值得到的初步结论，实际上根据张十庆、肖旻、俞莉娜、徐怡涛等学者的研究⑨，整数尺（寸）控制现象不仅限于平面柱网尺寸，也存在于柱高、屋架举高以及用材尺寸。

3 基于整数尺法的东大殿柱高、生起和剖面的尺寸分析

3.1 基于整数尺法的东大殿柱高和生起尺寸分析

根据清华大学的勘察，佛光寺东大殿的柱高实测尺寸如表4。

东大殿的柱高实测尺寸显示柱高尺寸个体差异较大，整体上呈现如下的规律：沿着开间方向，以心间的两棵柱子高度最低，并依次向角部逐渐抬高；沿着进深方向，以中柱的高度最低，并依次向角部逐渐抬高；西北部分柱高比西南部分柱高要高；后檐檐柱柱高普遍较低⑩。

根据清华大学的调研，柱高出现个体差异和上述规律的现象是以下三个原因所致；这栋建筑存在生起的做法；其次是基础变形、构架歪闪以及柱脚腐蚀使然；最后在勘察中发现部分后檐檐柱存在后代更换的现象⑪。考虑到上诉因素，清华大学对各柱柱高进行了推测复原如表5⑫。

其中外檐和内槽心间柱子以及两山中柱等高（h1=4 987.5 mm），为柱高最低者，外檐和内槽次间外柱和稍间外侧中柱等高（h2=5 040 mm），为柱高次低者。外檐部分次间、稍间、尽间每间外柱比内柱分别生起52.5 mm、73.5 mm、94.5 mm，角柱比平柱共生起220.5 mm；内槽部分次间、稍间每间外柱比内柱生起52.5 mm，内槽角柱比内槽平柱共生起105 mm。

h2=5 040 mm用唐尺1和唐尺2进行折算分别为：17.06唐尺和16.02唐尺，显然以唐尺2折算出来的尺寸更接近于整数尺。再来看生起尺寸（表6）。

从上表可以看出各间的生起以唐尺2=31.46 cm为单位的生起尺寸比以唐尺1=29.55 cm为单位的生起尺寸更为理想。例如外檐面阔方向从平柱开始逐间的生起尺寸（以唐尺2为单位）分别约为5/3唐寸、7/3唐寸以及3唐寸，总生起为7唐寸；而山面第二、三进的生起尺寸（以唐尺2为单位）均约为5唐寸，第一、四进的生起尺寸（以唐尺2为单位）均约为2唐寸，总生起亦约为7唐寸。而内槽柱开间进深方向各间的生起尺寸（以唐尺2为单位）均约为5/3唐寸，内槽柱面阔方向的总生起则约为10/3唐寸。

因此从柱高以及柱子生起尺寸来看仍以唐尺2（尺长约为31.46 cm）折算出来的尺寸值更为理想和合理。下面再来看东大殿屋架举高尺寸。

3.2 基于整数尺法的东大殿剖面尺寸分析

在清华大学的这次调研中，对剖面标高的测量“主要针对东大殿草栿大木梁架点云文件，测量对象为进深及开间方向各缝梁架槫距距离及标高值”，而点云图像显示槫材有歪闪和下沉的现象，课题组认为，这是综合变形影响的结果⑬，综合各项调查、分析以及研究，课题组最终对东大殿始建时的设计尺寸建立了理想模型，其中心间横剖面的尺寸复原如图2，此复原案的主要剖面尺寸如表7所示⑭。在这里本文也在表中将这些尺寸折算成唐尺1和唐尺2。

从上表来看，很难判断唐尺1和唐尺2在折算剖面尺寸中哪个更为理想。但是当对清华大学推测的剖面案进行Autocad作图分析，结果发现如果按举折之法，上平槫自橑风槫和脊槫的连线下折约311 mm，中平槫从这条连线下折475 mm，下平槫从这条折线下折325 mm⑮，这三个尺寸如果分别用唐尺1来折算分别为：1.05唐尺、1.61唐尺和1.10唐尺，如果用唐尺2来折算则分别为：0.99唐尺、1.51唐尺和1.03唐尺。从这三个尺寸来看以唐尺2折算的更为理想。也就是说，当初可能是在剖面设计中确定椽架平长为7唐尺，建筑总高39唐尺，平柱柱高已如前文分析来进行确定，再在其上安装铺作（铺作举高7.8唐尺、铺作出跳6.3唐尺）并据此确定橑风槫的位置，然后连接橑风槫和脊槫，并在上平槫、中平槫和下平槫位置分别下折1唐尺、1.5唐尺和1唐尺（图3）。

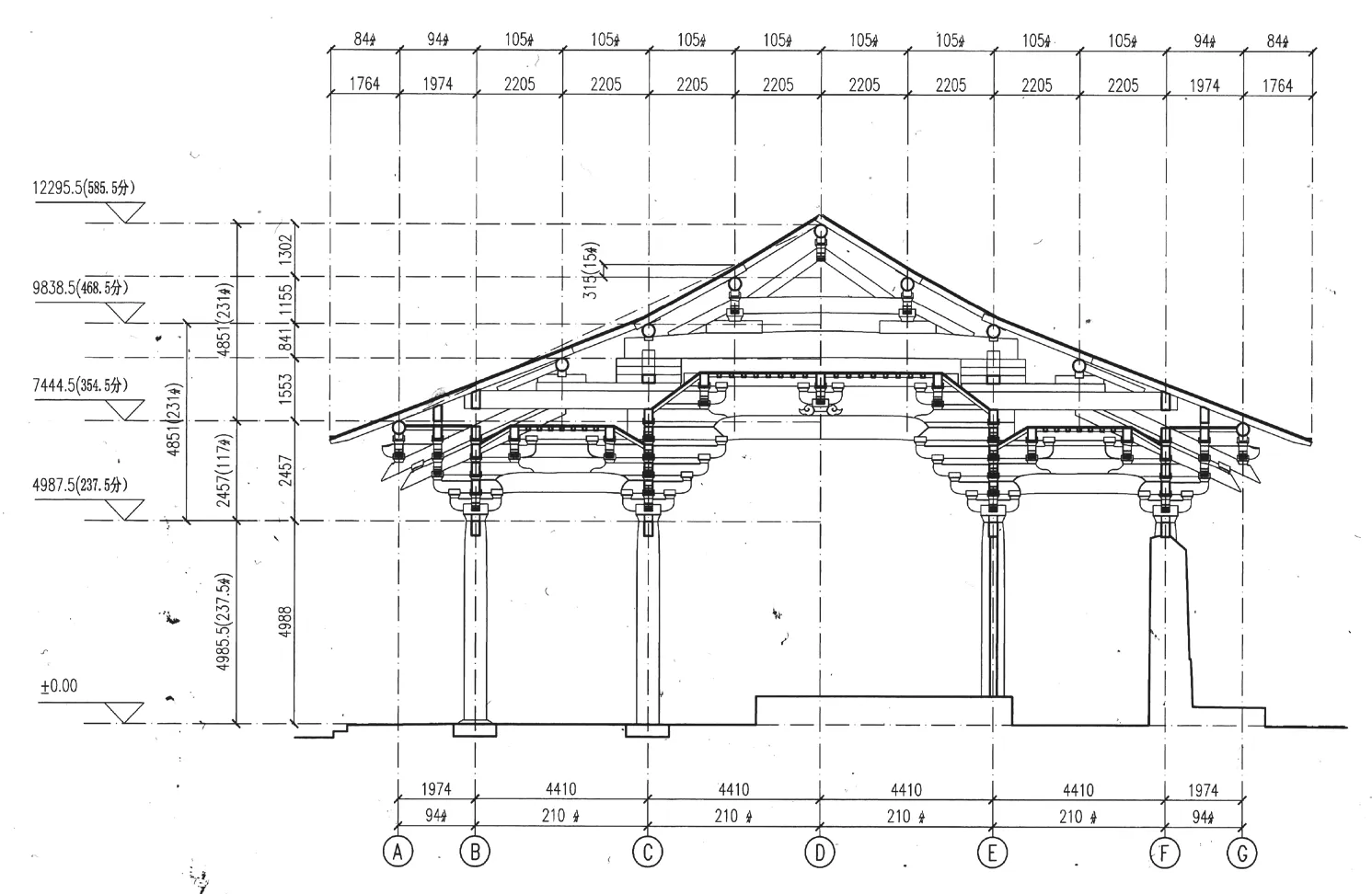
图2 佛光寺东大殿尺寸复原理想模型之明间横剖面（清华大学案）Fig.2 section of Main Hall in Fogongsi Temple (speculation scheme speculated by Tsinghua University)

表7 佛光寺东大殿剖面尺寸分析表Tab.7 analysis table of section size in Main Hall in Fogongsi Temple

从本文的分析来看，基于清华大学的心间横剖面复原案数据的屋面举折之法与北宋《法式》所记载的方法有相似之处，但是更为简洁、方便。相似的举折之法见于岭南：岭南的传统屋面曲线的形成是先定屋架总举高，然后在各槫材分位从橑风槫和脊槫的连线向下折。下折的尺寸分别从上至下和从下至上以总举高的百分率相互对称向中间增大，即最中央下折最多，从中间向脊槫和橑檐方下折尺寸逐渐变小，由此形成下凹的屋面曲线（图4）⑯。本案的下折也反映了这个规律，上平槫和下平槫均下折1唐尺，中平槫下折1.5唐尺，以中平槫为下折最大，上平槫和下平槫的下折则一致。相较于岭南的做法，本案更为简便易行——下折是整数尺寸更加便于操作。一般认为岭南地区的文化包括古建筑技术留存古制较多，结合本案的分析我们推测，本案推测的折屋方式可能是一种比较古老的做法。

图3 佛光寺东大殿明间横剖面举折推测方案Fig.3 section of Main Hall in Fogongsi Temple(speculation scheme of Juzhe)

值得注意的是，如果以唐尺2为单位，椽架平长也就是槫距恰好是7唐尺；另外，据清华大学的复原案，纵剖面中上平槫至架设脊槫增长的屋架⑰之水平距离为1 890 mm，而这个屋架到次间外轴水平间距为945 mm，这两个数值如果用唐尺1来折算分别是：6.40唐尺和3.20唐尺，而用唐尺2来折算则分别是6.01唐尺和3.00唐尺，也是以唐尺2更为理想。即纵剖面中上平槫至次间外轴的水平距离恰好是9唐尺，其中上平槫至架设脊槫增长的屋架的水平距离是6唐尺，而该屋架到次间外轴的水平距离恰为3唐尺。

下面再来看看东大殿的用材尺度。

4 对用材的尺寸分析

根据清华大学的测量和研究，该建筑材厚为210 mm左右⑱。《法式》规定，材厚10分，材广15分，栔广6分，足材21分，如果当初东大殿采用了和《法式》一致的材分比例，则材广315 mm，栔广126 mm，足材441 mm。将这些尺寸用唐尺1和唐尺2进行分析如表8。

从表中来看，由唐尺2（尺长约为31.46 cm）折算出来的用材尺寸都比较理想，尤其是材广刚好是1唐尺，这刚好是本文出发点“整数尺法”的基本模数。也就是换一个角度讲这栋建筑的整数尺法也可以视为我国“材分制”⑲设计的一个早期实例：即以材广1唐尺（尺长31.46 cm）为模数进行设计施工。

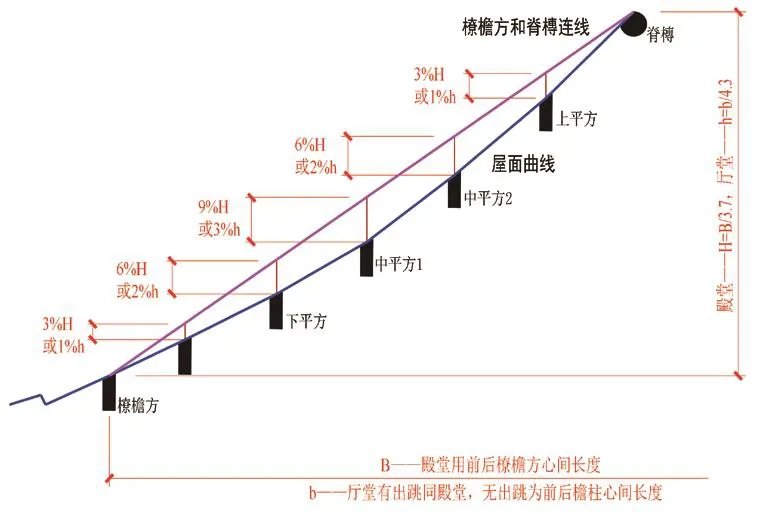
图4 岭南古建筑举折法Fig.4 traditional design method of roof section in South China

表8 佛光寺东大殿用材尺寸表Tab.8 measurement of module named cai in Chinese in Main Hall in Fogongsi Temple

值得注意的是，按照《法式》的规定以及清华大学的研究中所确定的材厚尺寸（约210 mm）计算出来的足材是441 mm，但是清华大学的报告中确定的足材尺寸却是431 mm。根据该书的分析，足材尺寸“略小的原因有可能由于作为横向用材的栱构件长期受压导致”，并且栌斗平欹高也同样出现了比《法式》的规定略低的情况，而两者的压缩比例接近：

栌斗平欹广压缩分值0.4分÷《法式》规定的栌斗平欹广12分=3.3%

足材广压缩分值0.5分÷《法式》规定的足材广21分=2.4%⑳。

另一个值得注意的现象是，清华大学确定的材厚尺寸如果以唐尺2为单位则正好是2/3唐尺，结合前文对各间柱子生起尺寸中存在1/3唐尺（以唐尺2为单位）的尺寸值，可以进一步推测在整数尺法角度对这栋建筑的实测尺寸分析的同时，1/3唐尺（以唐尺2为单位）也是一个比较重要的模数。

5 小 结

本文从整数尺法的角度分析了佛光寺东大殿2008年勘察报告中的实测数据发现，这栋建筑的营造用尺很有可能是1唐尺=31.46 cm。以这一尺长为单位：第一，东大殿的各个开间、进深的柱头尺寸都是整数尺；第二，该建筑有10根柱子的柱高亦为整数尺并与该建筑中央五间的开间值一致，而其他的柱子与这10根柱子之间存在理想尺寸的生起做法；第三，该建筑的屋架举折控制尺寸亦接近于整数尺寸，而我们推测的举折之法与岭南地区的举折之法有极为近似之处；最后，该建筑的用材尺寸亦为极为理想的整数尺寸。值得注意的是，在用材尺寸和生起尺寸中都存在以唐尺2（尺长约31.46 cm）为单位的1/3唐尺这一模数。另外由于该建筑的材广刚好是1唐尺（以唐尺2=31.46 cm为单位），因此本建筑中呈现的整数尺控制现象亦可为我国早期“材分制”做法的一个例证。

本研究一方面深入探讨了我国现存最重要的唐构佛光寺东大殿的尺度问题，另一方面也有助于对东亚早期建筑设计方法的整数尺法、“材分制”的深入认识，最后对丰富东亚尺度史研究也有积极意义。

但是本研究仍然留下两个问题期望在未来得到解决：第一，本文对柱高、生起以及屋面举折尺寸的分析的数据基础是清华大学对实测数据进行分析研究的结果，而并非直接分析实测数据，因此如果清华大学的相关研究被修正本文的研究也有修正的必要；第二，本文所发现的1/3唐尺目前仅控制材厚和生起尺寸，还没有发现对其他细部尺寸的控制现象，因此1/3唐尺的模数的存在仍有待更进一步的调查和分析。

注释：

① 据我们统计现存唐代遗存有：南禅寺大殿（782年）、广仁王庙正殿（831年）、佛光寺东大殿（857年）、莫高窟第196窟窟檐（893年）、天台庵正殿（唐）和开元寺钟楼（晚唐）。其中莫高窟第196窟窟檐仅存乳栿以下的唐代构架，根据萧默的研究，此窟檐的创建年代在893年（《敦煌建筑研究》337页）。开元寺钟楼只有底层梁架、斗拱、用柱、墙体和门窗等保留晚唐风格（《正定开元寺钟楼落架和复原性修复》）。

② 详情见吕舟《佛光寺东大殿建筑勘察研究报告》第24-25页。

③ 详情见张十庆《中日古代建筑大木技术的源流与变迁》第73页。

④ 张十庆在其博士论文中分析了2栋唐代遗构、2座唐代房屋遗址、5栋辽代建筑以及6栋北宋遗存，发现其中也存在着整数尺控制现象，而部分遗存开间尺寸还涉及到半尺。张十庆《中日古代建筑大木技术的源流与变迁》73-92页。

⑤ 丘光明《中国物理学史大系·计量史》360-367页。这40把唐尺中有一把推算出来的唐尺尺长25.7 cm，显然与一般唐大尺的认识相悖，而与一般认识的唐小尺尺长相约。

⑥ 吴承洛《中国度量衡史》58-59页，“中国度制以尺为单位，及其为用，有三种分划，即尺之为实用单位有三个系统”，“律用尺 木工尺 衣工尺（裁尺）”。

⑦ 详情见吴承洛《中国度量衡史》第298-303页。

⑧ 清华大学课题组也曾经推演出中央五间为16唐尺的可能性（《佛光寺东大殿建筑勘察研究报告》122页）。

⑨ 《唐宋古建筑尺度规律研究》《宁波保国寺大殿勘测分析与基础研究》《山西万荣稷王庙大殿大木结构用材与用尺制度探讨》等。

⑩ 吕舟《佛光寺东大殿建筑勘察研究报告》第88页。

⑪ 吕舟《佛光寺东大殿建筑勘察研究报告》第88页，被后世替换的柱子具体是表3中带框的数据所对应的后檐檐柱。

⑫ 清华大学对柱子原高以及生起的推测是基于所有柱头标高测量尺寸进行复原，在推算之初首先排除后期更换柱子和明显沉降柱头干扰，并采信部分柱头标高。采信标准为：柱础无明显沉降的前檐柱；排除侧脚因素——柱身基本无偏移；同样条件下的柱子采信柱高较高者——在建筑变形过程中柱高变高的可能性较小。最终采取前檐心间高度较高的北缝柱头标高4 991.2 mm为平柱高度，其他柱头生起值以此为基础测算。

⑬ 详情见吕舟《佛光寺东大殿建筑勘察研究报告》第74-75及89-101页。

⑭ 屋面举折所涉及的尺寸主要在于槫距以及各槫材的标高。清华大学的研究是针对东大殿的点云数据进行分析。槫距的点云数据显示在前后压槽方之内的各槫距的实测值（实测值对应的是槫材下方的卯口水平间距）离散量不大，均值略大于分间进深之半（差值为12 mm），课题组认为这是由于槫子向外滚动引起替木、承槫斗拱和卯口的变形导致针对卯口的实测值偏大，由此推测槫距均等，为分间进深之半。考虑到柱子生起的影响，关于屋面举折的分析集中于心间：横剖面的理想模型是基于对心间槫材顶端标高的点云数据的分析。点云数据显示后檐槫高均低于对应之前檐槫材，高度差从上平槫至橑风槫逐渐增加，课题组认为这是后檐檐柱被更换和有较大沉降所致，因此以心间前檐的数据为参考值，再根据前面推测的平柱高以及基于材分制分析确定的铺作高推测橑风槫的高度位置。

通过比较前后檐的屋架总举高（心间与次间数据求平均）与前后橑风槫间的水平间距的比值可以看出，脊槫相对于前后橑风槫的起坡相差无几，因此课题组将次间和心间的脊槫相对于前后橑风槫的举高求平均，将此均值作为屋架总举高的参考。课题组发现橑风槫与按此举高举起的脊槫之间的连线与下昂坡度基本一致，据下昂坡度和橑风槫至脊槫的水平距离求得的高度值与前述参考举高值非常接近，并且正好是材厚的23倍，而这个直角三角形也刚好是下昂直角三角形的11倍。据此以材厚的23倍为屋架总举高。另外通过对实测数据的分析，课题组发现中平槫至平柱顶的高度值与屋架总举高非常接近——可以视为同一，由此确定了中平槫的高度。同时课题组基于对点云的分析发现，上平槫是通过从橑风槫与脊槫的连线下折312 mm，约当1材得到，而下平槫和牛脊槫则正好在中平槫和橑风槫的连线上。至此课题组对东大殿的屋面曲线进行了完整复原。

⑮ 有关中平槫和下平槫高度位置的确定，本文与清华大学的复原案有一些出入：本文认为如果清华大学心间横剖面的复原案无误，中平槫和下平槫有可能也是通过下折得到，而非通过平柱上举一定的高度确定中平槫，再连线中平槫和橑风槫得到下平槫的位置。

⑯《南海神庙大殿复原研究（三）南北古建筑木构架技术异同初论》41页，而据《广东古代殿堂建筑大木构架研究》这种折屋之法为岭南地区广府建筑所特有（《广东古代殿堂建筑大木构架研究》149页）。

⑰ 即清华大学复原案中所说之 外叉手”，下同。

⑱ 如果将这个材厚用唐尺1折算则约为0.71唐尺，若用唐尺2折算则为0.67唐尺，均超过了《法式》所规定的最高材等一等材之材厚（6寸）。

⑲ 材分制 这一名词最早由陈明达提出，他指出：“《营造法式》，给我们的重要贡献之一，就是相当详细地记录、阐述了当时已通行的建筑和结构设计所应用的材分制，亦即古代的模数制。”（《营造法式大木作制度研究》6页），这个研究对国内学术界产生了深远的影响，“材分制 随之成为《法式》中所载模数制的代称。之后根据傅熹年的研究，这种模数方法出现的时间有可能可以上推至南北朝时期（《日本飞鸟、奈良时期建筑中所反映出的中国南北朝、隋、唐建筑特点》）。因此本文所说 材分制是指与《法式》所载的这种模数制相类似的做法，并不局限于专指《法式》所记载的北宋的一种 模数制”。

⑳ 《佛光寺东大殿建筑勘察研究报告》105页。

参考文献：

[1] 清华大学建筑设计研究院，北京清华城市规划设计研究院，文化遗产保护研究所.佛光寺东大殿建筑勘察研究报告[M]. 北京: 文物出版社, 2011.

[2] 张十庆. 中日古代建筑大木技术的源流与变迁[M]. 天津: 天津大学出版社, 2004.

[3] 吴承洛. 中国度量衡史[M]. 北京: 商务印书馆, 1937.

[4] 丘光明. 中国物理学史大系·计量史[M].长沙: 湖南教育出版社, 2002.

[5] 东南大学建筑研究所. 宁波保国寺大殿勘测分析与基础研究[M]. 南京: 东南大学出版社, 2012.

[6] 肖旻. 唐宋古建筑尺度规律研究[D]. 广州:华南理工大学博士学位论文, 2002.

[7] 肖旻. 唐宋古建筑尺度规律研究[M]. 南京: 东南大学出版社, 2006.

[8] 俞莉娜, 徐怡涛. 山西万荣稷王庙大殿大木结构用材与用尺制度探讨[J]. 中国国家博物馆馆刊, 2015(06): 128-146.

[9] 李诫. 营造法式[M]//台湾商务印书馆股份有限公司. 景印文渊阁四库全书（第0673册）[G]. 台北: 台湾商务印书馆, 1984.

[10] 梁思成. 记五台山佛光寺建筑[J]. 中国营造学社汇刊. 1944(07): 13-61.

[11] 梁思成. 记五台山佛光寺的建筑[J]. 文物参考资料, 1953(5/6): 76-89.

[12] 山西省古建筑保护研究所. 佛光寺[M].北京: 文物出版社, 1984.

[13] 柴泽俊. 佛光寺东大殿建筑形制初析[J].五台山研究, 1986(01): 17-20.

[14] 山西古建研究所. 山西古建筑木结构模型[M]. 北京: 燕山出版社, 1989: 22-25.

[15] 陈明达. 营造法式大木作制度研究[M].北京: 文物出版社, 1992.

[16] 傅熹年. 五台山佛光寺建筑[M]//傅熹年.傅熹年建筑史论文集. 北京: 文物出版社,1998: 234-244.

[17] 傅熹年. 中国古代城市规划、建筑群布局及建筑设计方法研究[M]. 北京: 中国建筑工业出版社, 2001: 95-97.

[18] 萧默. 敦煌建筑研究[M]. 北京: 文物出版社, 2003.

[19] 聂连顺, 林秀珍, 袁毓杰. 正定开元寺钟楼落架和复原性修复（上）[J]. 古建园林技术, 1994(01): 48-52.

[20] 聂连顺, 林秀珍, 袁毓杰. 正定开元寺钟楼落架和复原性修复（下）[J]. 古建园林技术, 1994(02): 11-15.

[21] 程建军. 南海神庙大殿复原研究（三）南北古建筑木构架技术异同初论[J]. 古建园林技术, 1989(04): 41-47.

[22] 程建军. 广东古代殿堂建筑大木构架研究[D]. 广州: 华南理工大学, 1997.

[23] 张毅捷. 日本古代楼阁式木塔研究[D].上海: 同济大学, 2011: 68-71.

[24] 张毅捷. 两座日本古塔的建筑平面设计分析[A]//贾珺. 建筑史[C]. 北京: 清华大学出版社, 2014(34): 197-204.

图表来源：

图1：根据《佛光寺东大殿建筑勘察研究报告》及《中日古代建筑大木技术的源流与变迁》改绘（图内尺寸为张十庆推测的平面柱网设计值）

图2：摘自《佛光寺东大殿建筑勘察研究报告》120页图4-26

图3：根据《佛光寺东大殿建筑勘察研究报告》276-277页《明间横剖面图》改绘

图4：临摹自《南海神庙大殿复原研究（三）南北古建筑木构架技术异同初论》41页图25c