邓克利法求解基频的精度研究

张 翔,杨 怡,张 红

(华南理工大学 土木与交通学院,广州 510640)

线性多自由度系统的自由振动问题可以简化为刚度矩阵和质量矩阵的广义本征值问题.系统的自由度越多,本征值问题的计算量就越大,可以通过计算机作数值计算以得到准确的结果;同时,出于工程计算的实用性,可对多自由度系统的振动特性作近似估算[1].常用的近似计算方法有邓克利法、瑞利法、里兹法、矩阵迭代法、子空间迭代法等,基于这些近似算法,学者们[2-4]也提出了一些改进方法.这些方法全部是从原方法理论推导着手,通过优化其中推导过程减小误差,从而达到改进的目的.

在以上方法中,邓克利法是最为简单的一种计算方法.作为一种振动特性的近似估算方法,邓克利法给出了系统基频的下限,可以对链式系统的基频作近似估算,应用于土木工程、航空航天、机械汽车等多个领域.在国内研究领域,王开宇等[5]运用邓克利法估算离心式,给水泵中转子自激励振动频率,判断数值解的可靠性.黄震等[6]运用邓克利法建立了高频响测力仪的简化模型,推导了固有频率的解析解.朱成实等[7]对数控机床主轴的力学模型应用邓克利法,计算得到一阶固有频率近似值.石元华等[8]以飞机的整体结构频率为目标,基于邓克利法和瑞利法估计夹具的基频范围,以确定夹具的结构形式.在国际研究领域,Levy[9]对有关邓克利法估算基频的迭代法进行了研究.Low[10]对邓克利法在建筑领域集中质量梁模型的基频估算方面进行了一定的方法研究和改进.

邓克利法虽然简单方便,但同时也是计算误差最大的一种方法.为了降低该方法的误差,推广其应用范围,不少研究者[11-12]对邓克利法计算公式进行了修正,给出了改进的邓克利公式.这些工作集中于20世纪末,对于邓克利法估算误差改进的工作，大多只是在邓克利法公式中稍作理论计算的优化近似,从而得到改进后的邓克利法,受计算机条件限制,无法在大量数据的基础上进行分析，对邓克利法准确度影响因素的系统研究,也没有建立在对基频估算误差系统分析基础上对邓克利法的改进.本文针对集中质量梁模型和质量弹簧模型,在不同的约束条件和自由度情况下，研究邓克利法基频解的误差变化规律,讨论邓克利法精确度的影响因素,并对计算结果进行数值拟合,给出改进的邓克利法计算公式.

1 集中质量梁模型

考虑如图1所示的集中质量梁模型，梁段的刚度和长度为EI和L,所有质量都集中在质点m.为简单起见,假设所有梁段和质点具有相同的力学属性.图1(a)为悬臂梁,图1(b)为简支梁.用邓克利法求解这两种梁模型的基频与解析解的误差.

图1 集中质量梁模型Fig.1 Beams with lumped mass

令模型自由度从1～10变化,分别运用邓克利法和普通解析法,求解悬臂梁模型、简支梁模型的基频估算值和精确值,具体计算方法可见文献[1].对比基频的邓克利法解和解析解,结果如表1和表2所示.为简化表达式,令EI/(m3l)=1.

表1 悬臂梁模型的基频计算结果Tab.1 Basic frequencies of cantilever beams

表2 简支梁模型的基频计算结果Tab.2 Basic frequencies of simply supported beams

由表1和表2可知:邓克利解都小于解析解,随着自由度的增加,邓克利解的误差逐步增大;而且在相同自由度下,简支梁模型邓克利解的误差大于悬臂梁模型,这是因为悬臂梁第1阶和第2阶频率的平方倒数之差要比简支梁的大,邓克利法计算的基频与精确值的误差就会比较小.

2 质量弹簧模型

考虑如图2所示的质量弹簧模型.弹簧段的刚度为k,其质量不计,所有质量都集中在质点m,忽略系统的阻尼.图2(a)为左端约束,图2(b)为两端约束.

令系统的自由度从1～10变化,分别运用邓克利法和普通解析法求解图2(a)和图2(b)两种模型的基频,计算结果见表3和表4.为简化表达式,令k/m=1.

由表3和表4可知：对于一端约束和两端约束的质量弹簧系统,随着自由度的增加,邓克利解的误差逐步增大;而且在相同自由度下,两端约束模型邓克利解的误差要远大于一端约束模型,超过其误差的2倍.通过对固有频率解析解的分析,发现第1阶频率平方的倒数在所有频率平方的倒数和中所占的比例随着自由度的增加而增大,且一端约束模型的这个比例值比两端约束模型要高出10%,所以前者的邓克利解误差就比后者小很多.

图2 质量弹簧模型Fig.2 Mass-spring system

3 结果分析

3.1 误差分析

图3是前面所用梁模型和质量弹簧模型,用邓克利法计算其基频的结果误差随自由度的变化曲线图.可以发现,对于各类模型运用邓克利法进行基频估算时,误差会随系统自由度的增加而增大,在低自由度时误差增长较快,在高自由度时误差变化趋于平缓,并近似于线性变化.在相同自由度下,简支梁的误差大于悬臂梁,双约束质量弹簧系统的误差大于单约束模型,模型的约束越多,邓克利法解的误差就越大,且梁模型的误差比质量弹簧模型要小很多.

表3 左端约束质量弹簧模型的基频计算结果Tab.3 Basic frequencies of mass-spring models with left end restrained

表4 两端约束质量弹簧模型的基频计算结果Tab.4 Basic frequencies of mass-spring models with two ends restrained

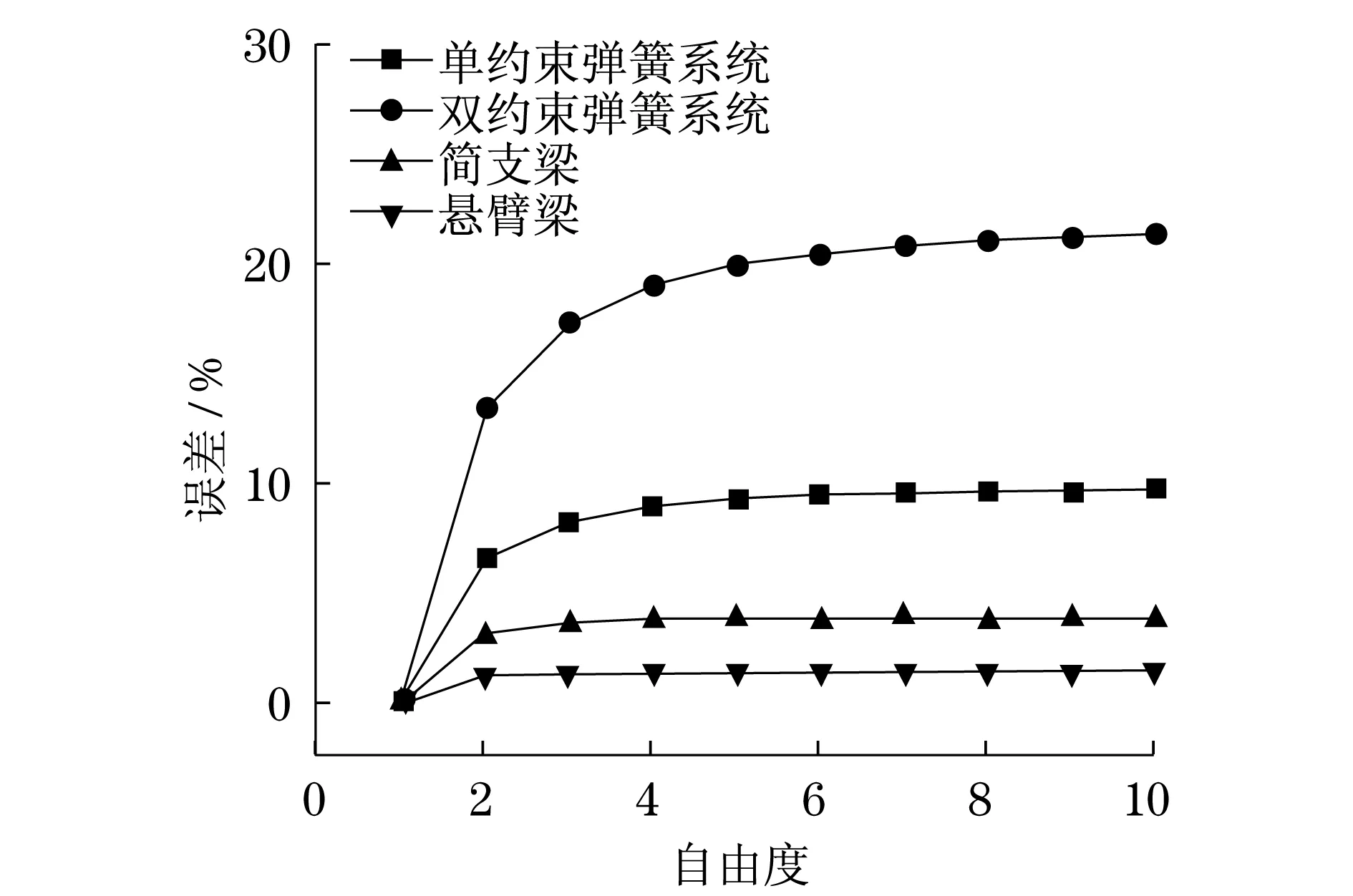
图3 各类模型邓克利法的计算误差Fig.3 The calculation errors of the basic frequency

3.2 数值拟合

由3.1节中给出的用邓克利法计算4种模型的基频误差随自由度的变化曲线,可以发现,误差值在最初1,2或3自由度时变化较大,在之后随着系统的自由度增加,误差值的增大基本趋于线性变化,但不同系统误差趋于线性变化时,对应的自由度开始点不同.故在图3的误差曲线中,取接近于直线的部分进行线性拟合,以对自由度在10以上时的误差进行估算.拟合结果如图4所示.

在图4中,各模型的线性拟合方程分别为

悬臂梁:

(1)

简支梁:

(2)

左端约束弹簧系统:

(3)

两端约束弹簧系统:

(4)

式中:y为误差值;n为自由度;R2为拟合度.

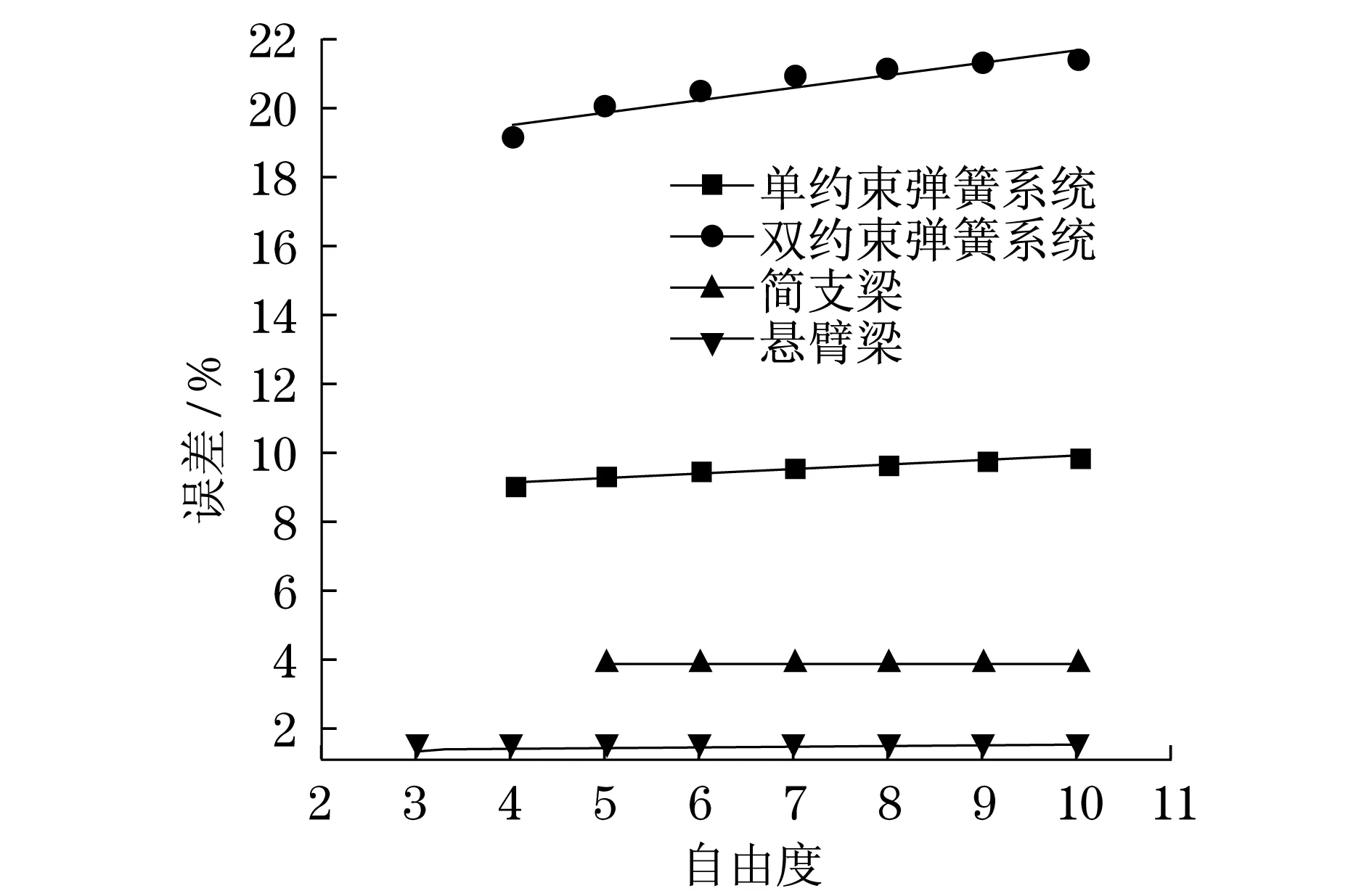
图4 各类模型邓克利法估算误差的线性拟合Fig.4 Linear fitting of the calculation errors

3.3 误差修正

根据3.2节给出的线性拟合方程,可以对各模型邓克利解进行修正,以提高自由度大于10以后的基频解的精度.设各个模型的基频解析值为f0,普通邓克利法估算基频为f1,普通邓克利法估算误差随自由度变化的拟合线性函数为y(n),改进邓克利法基频解为f2.

普通邓克利法基频解的误差为

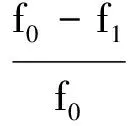
(5)

由误差线性拟合方程可知,改进后邓克利法解应满足

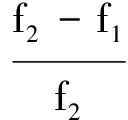
(6)

于是,得到邓克利法的改进公式为

(7)

将改进邓克利公式(7)代入方程(1)～(4),可以写出4种模型的改进邓克利法基频解：

悬臂梁:

(8)

简支梁:

(9)

左端约束弹簧系统:

(10)

两端约束弹簧系统:

(11)

为验证式(8)～(11)的精度,对各模型分别取自由度为11～14,采用解析法、普通邓克利法和改进邓克利法计算其基频,并分析误差,计算结果如表5所示.

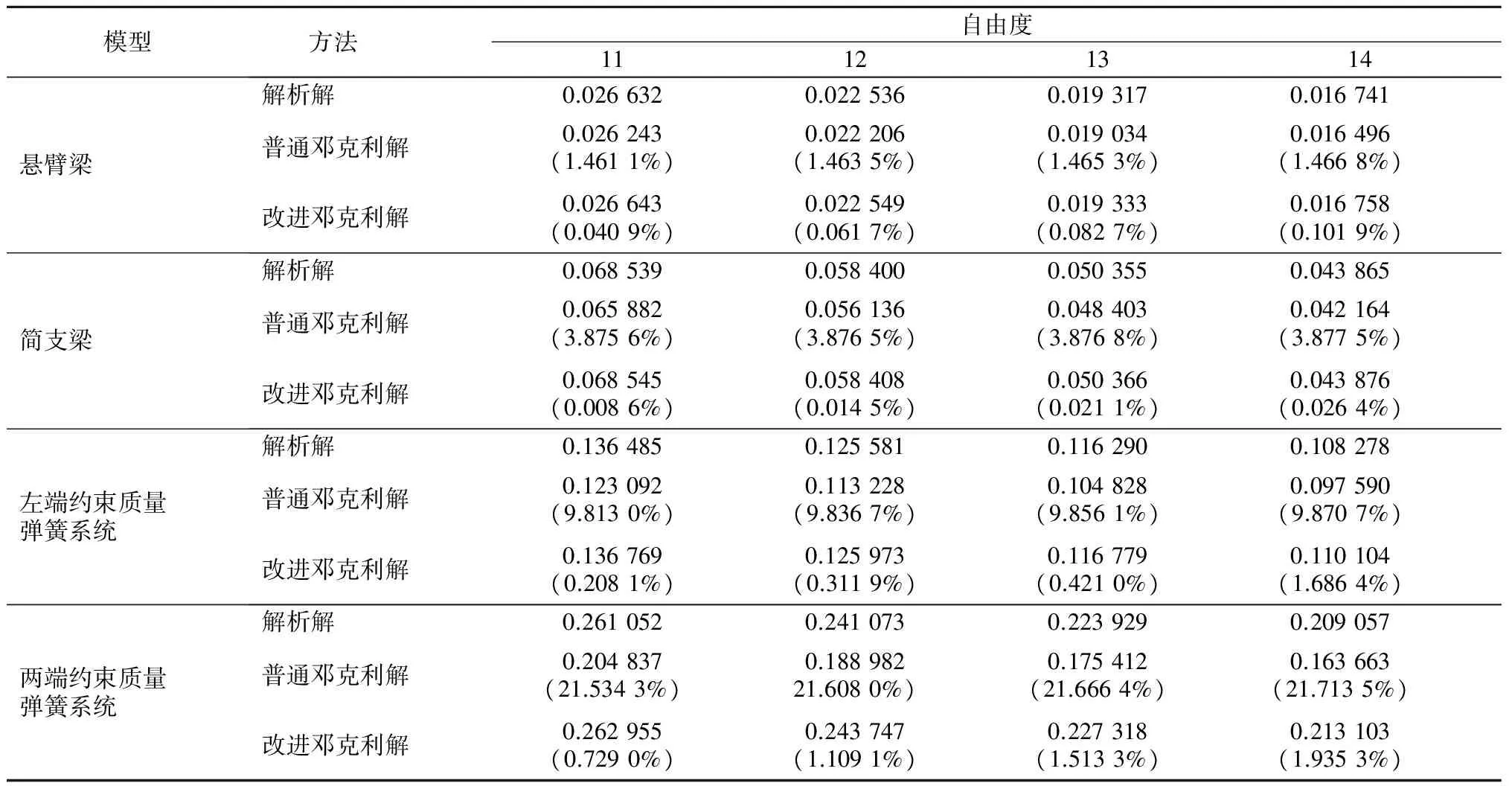
表5 自由度为11～14时系统的基频Tab.5 The basic frequencies of the systems when degree-of-freedom equals 11 to 14

注:括号内数值表示邓克利解的误差.

由表5可以发现：改进邓克利法在大自由度下,可大大降低基频的误差值,对于集中质量梁结构,误差只在万分之一量级;对于质量弹簧系统,误差不超过2%,主要是因为改进邓克利法需要以普通邓克利法为基础,而此时普通邓克利解的误差偏大,使得改进邓克利解的误差增大.由此可见,改进邓克利法有效提高了邓克利法在系统大自由度下对基频估算的精确度.

4 结论

本文对邓克利法在集中质量梁结构和质量弹簧系统中求解基频的精度进行了研究,讨论了结构形式和自由度数目对邓克利解精度的影响,并对误差进行了分析,提出改进邓克利法的求解公式.主要结论有:

(1) 相同自由度下,同一类模型中约束较多的系统邓克利法的误差较大.简支梁的误差比悬臂梁大,两端约束质量弹簧系统比一端约束系统大.

(2) 对同一个模型,随着自由度的增加,邓克利法的误差逐渐增大;在低自由度时,误差增大明显,在自由度较大时误差增大趋缓.

(3) 利用文中给出的改进邓克利法公式,对高自由度系统进行基频计算,能大大提高邓克利解的精度.

(4) 在相同的约束个数和自由度下,质量弹簧系统的邓克利法估算误差大于集中质量梁系统.可见在实际工程中,相同工况下可选用邓克利法优先精确估算梁系统基频.

参考文献:

[1] 刘延柱,陈立群,陈文良.振动力学[M].2版.北京:高等教育出版社,2011.

LIU Y Z,CHEN L Q,CHEN W L.Vibration mechanics[M].2nd ed.Beijing:High Education Press,2011.

[2] 陈玉骥.一种计算多自由度结构基频的较简便方法[J].力学与实践,2013(6):75-77.

CHEN Y J.A simple method for calculating the basic frequency of multi-degree freedom system[J].Mechanics in Engineering,2013(6):75-77.

[3] 陈奎孚,张森文.估计多自由度系统振动基频的一个算法[J].机械强度,2003(2):141-143.

CHEN K F,ZHANG S W.Algorithm to estimate the minimum natural frequency of multi-degree freedom vibration system[J].Journal of Mechanical Strength,2003(2):141-143.

[4] 康婷,许金余,白应生,等.梁基本频率和振型的简便计算[J].四川建筑科学研究,2010(5):134-136.

KANG T,XU J Y,BAI Y S,et al.A simple method for calculating the fundamental frequency and mode shape of the beam[J].Sichuan Building Science,2010(5):134-136.

[5] 王开宇,伊洪丽,王宇,等.密封间隙力对泵转子临界转速的影响分析[J].机电产品开发与创新,2014(3):107-109.

WANG K Y,YI H L,WANG Y,et al.Analysis on the influence of the critical speed for the forces in annular seals[J].Development & Innovation of Machinery & Electrical Products,2014(3):107-109.

[6] 黄震,赵威.高频响测力仪固有频率的理论分析与试验[J].中国机械工程,2015(1):7-11.

HUANG Z,ZHAO W.Theoretical calculation and experimental analyses of natural frequency for high frequency dynamometer[J].China Mechanical Engineering,2015(1):7-11.

[7] 朱成实,勾延生,李铁军,等.基于改进PSO算法的数控机床主轴优化设计[J].中国机械工程,2015(20):2784-2788.

ZHU C S,GOU Y S,LI T J,et al.Optimization design of CNC machine tool spindle based on improved PSO algorithm[J].China Mechanical Engineering,2015(20):2784-2788.

[8] 石元华,邓俊,田俊丰,等.采用邓柯莱法和瑞利法的振动夹具设计[J].重庆理工大学学报(自然科学版),2013(9):97-101.

SHI Y H,DENG J,TIAN J F,et al.Design of vibration testing fixture based on the Dunkerley and the Rayleigh method[J].Journal of Chongqing University of Technology(Natural Science),2013(9):97-101.

[9] LEVY C.Iterative technique based on the Dunkerley method for determining the natural frequencies of vibrating systems[J].Journal of Sound and Vibration,1991,150(1):111-118.

[10] LOW K H.Modified Dunkerley formula for eigenfrequencies of beams carrying concentrated masses[J].International Journal of Mechanical Sciences,2000,42(7):1287-1305.

[11] 程桂胜.用修正的Dunkerley公式计算结构的基频[J].河北建筑工程学院学报,2000(3):6-8.

CHENG G S.To calculate the fundamental frequency of the structure using revised Dunkerley formula[J].Journal of Hebei Institute of Architectural Engineering,2000(3):6-8.

[12] 张春良.一种计算固有频率的新方法[J].机械,1995(5):24-27.

ZHANG C L.A new method for calculating natural frequencies[J].Machinery,1995(5):24-27.