无线传感器网络中基于BP-UKF的室内定位算法

贺 彬 ，吕晓军 ，张春家 ，杨 波

（1.山西大学 数学科学学院，太原 030006；2.中国铁道科学研究院 电子计算技术研究所，北京 100081）

无线传感器网络中基于BP-UKF的室内定位算法

贺 彬1，吕晓军2，张春家2，杨 波1

（1.山西大学 数学科学学院，太原 030006；2.中国铁道科学研究院 电子计算技术研究所，北京 100081）

针对复杂室内环境中的定位噪声问题，文中提出一种基于BP-UKF的室内定位算法。利用BP神经网络拟合任意非线性函数的特性训练样本集，以确定接收信号强度指示（RSSI）和距离之间非线性关系，进而估计待定位节点与锚节点间的距离；采用三边定位法计算待定位节点的坐标初始值，并利用无迹卡尔曼滤波（UKF）处理非线性系统方程；通过设距离的估计值为观测变量，对待定位节点坐标的初值进行精确化处理。仿真试验结果表明，对于较复杂环境的室内定位，与传统的定位算法相比较，文中所提BP-UKF算法实现达到更可靠和准确的位置估计。

室内定位；BP神经网络；三边定位；无迹卡尔曼滤波；非线性函数；无线传感器网络

目前的研究中，基于RSSI的定位算法分为两类：一类是基于模型的定位如基于路径损耗模型[4]，由于在不确定且时变噪声的室内定位环境中，RSSI的准确测量会受到很大的影响，使得在使用某一确定模型进行定位时，距离的估计误差增大，进而影响对未知节点坐标的估计。另一类是基于映射的定位[5]，该方法是通过已知数据信息建立RSSI与节点间距离的映射关系，虽然在映射关系建立的过程中，需要消耗一定的时间，但克服了基于模型算法的一些局限性，适用范围较广，定位更准确。

在基于映射的定位中，神经网络已经取得非常广泛的使用，其中BP（back-propagation）神经网络的优势尤为明显[6]。文中使用BP神经网络对RSSI与距离之间的非线性关系进行拟合。为了更精确化BP神经网络的定位结果[7]，提出了多种滤波方法如卡尔曼滤波、粒子滤波等[8]。其中，粒子滤波有较大的时间复杂度，不适于能量有限的WSN（wireless sensor network）中，而卡尔曼滤波在噪声存在的环境下是一种优选的状态估计器，且运行速度较其他滤波器快[9]。由于在室内环境中噪声的不确定性，传统的卡尔曼滤波器已不再适用，文中选择无迹卡尔曼滤波算法进行定位结果的优化。相比于扩展卡尔曼滤波器，该滤波器不需要对非线性函数进行线性化，因为线性化的过程会导致节点定位不准确。

1 室内定位模型

1.1 BP神经网络

在此选择BP神经网络来拟合RSSI和距离之间的非线性关系。BP神经网络是神经网络中使用最广泛的模型之一，经Kolmogorov定理验证BP神经网络可以逼近任何非线性函数[10]。BP算法可以是一个三维结构或更多结构的神经网络，通过验证，文中所取三维结构的神经网络可以达到预设的精度要求，具体包括输入层、一层隐含层和输出层，如图1所示。

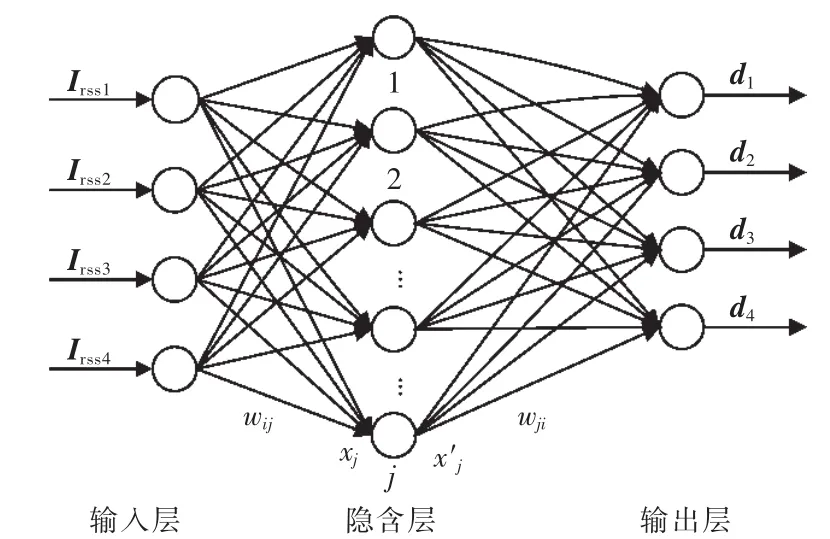
图1 三层BP神经网络结构Fig.1 Three-layer BP neural network structure

BP神经网络的训练过程包括数据的正向传播和误差的反向传播。文中Irss，i为第i个锚节点与所有信标节点之间的RSSI；作为BP神经网络的输入向量，试验中设置4个锚节点即输入向量的维度为4，如图所示；相应地，di为节点间的物理距离即输出向量。大量试验验证文中隐含层的神经元数取26。

BP神经网络的流程如2所示。

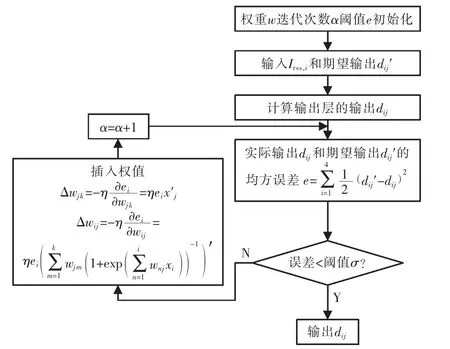
图2 BP神经网络训练权值的流程Fig.2 BP neural network training weights flow chart

1.2 三边定位法

利用三边定位法，在已知锚节点、未知节点与锚节点间的物理距离的情况下，计算未知节点的坐标以实现定位。即取3个锚节点为圆心，待定位节点i与3个锚节点间的距离为半径作圆，则3个圆的交点坐标即为未知节点i的估计坐标（Xi，Yi）。一般来说，因为对节点间距离的估计存在偏差，3个圆并不能相交于1个点而是形成一个区域，故很难决定准确的位置尤其是在大的噪声存在的情况下，如图3所示。

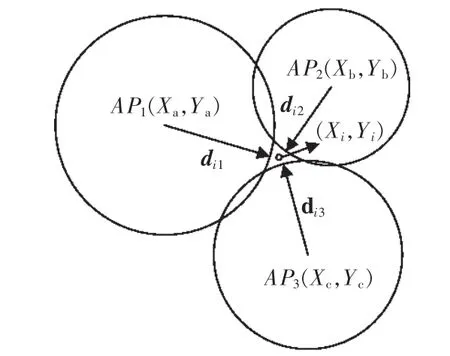
图3 三边定位的原理Fig.3 Trilateration principle

1.3 无迹卡尔曼滤波

取未知节点的坐标值（X，Y）为状态向量Xk，BP神经网络的输出向量即未知节点与锚节点间的距离估计值d为观测向量Yk，则以上所求的坐标为状态向量的初始值X0。

考虑非线性系统方程为

式中：Xk∈Rn为状态向量；Yk∈Rm为观测向量；Wk-1，Vk-1分别为相互独立的系统过程噪声和测量噪声，均为非加性噪声并满足约束：p（W）～N（0，Q），p（V）～N（0，R），其中Q，R分别为两类噪声的协方差矩阵。系数矩阵 A=［1， 0 ；0，1 ］T，非线性函数 h（·）为节点间的欧几里得距离公式。

无迹卡尔曼滤波UKF（unscented Kalman filter）的具体过程如下：

步骤 1 sigma 点集｛χi，i=0，1，2，…，2n｝的选择。

对k-1时刻的状态向量Xk-1进行采样时，取第1 个 sigma点 χ0，k-1=μ，余下的 2n 个 sigma点关于均值对称，即

其中

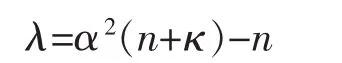
式中：μ，Σ分别为状态向量的均值和协方差矩阵；α，κ，λ分别为3个可调参数。

用sigma点表示k-1时刻状态向量Xk-1的均值和协方差分别为

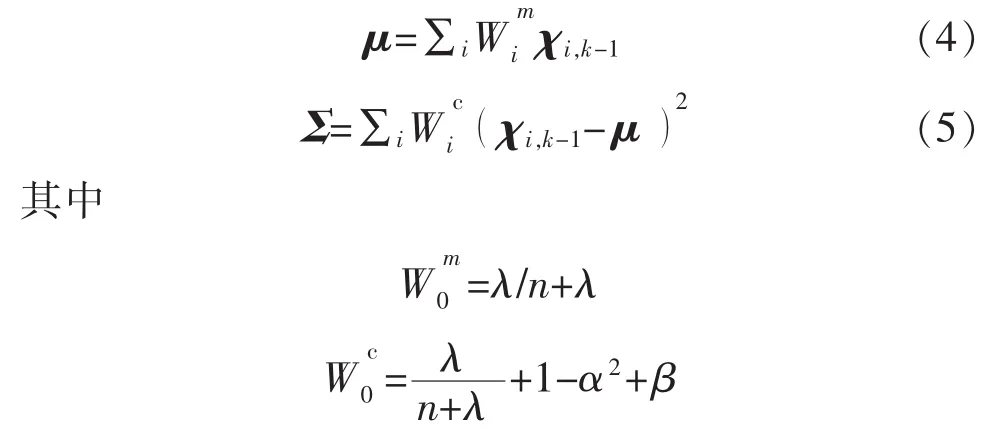
步骤2 时间预测阶段为

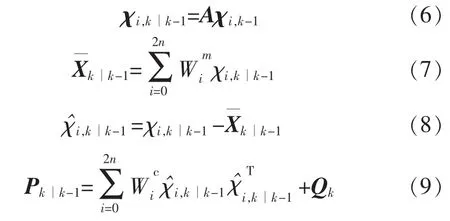
式（6）和式（7）为k时刻的一步预测sigma点集｛χi，k∣k-1，i＝0，1，…，2n｝的计算，并通过加权处理后获得一步预测状态向量k∣k-1。 Pk∣k-1为一步预测状态向量的误差协方差矩阵。

步骤3 测量值更新阶段为

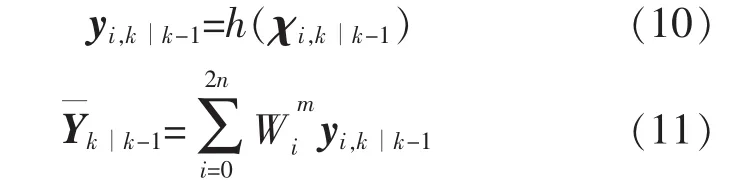
式（10）和式（11）为基于一步预测sigma点集通过非线性观测方程传递，并加权后获得k时刻的观测向量估计值k∣k-1。

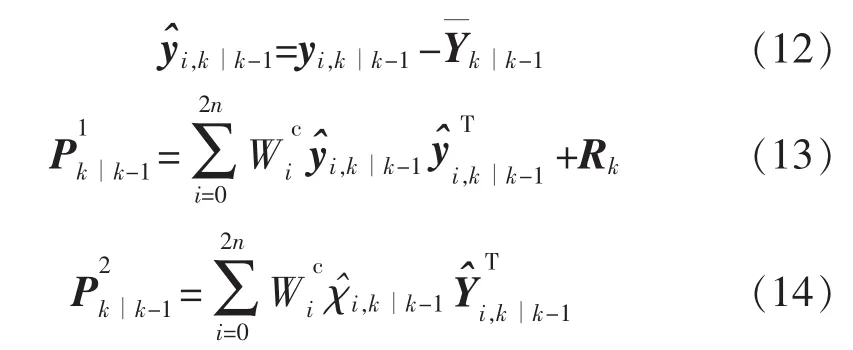
式（13）和式（14）分别为k时刻观测向量的协方差矩阵及观测向量和状态向量之间的交叉协方差矩阵。

经过计算，测量方程是线性的，因此可以使用与经典卡尔曼滤波器相同的方程实现更新。具体过程如下：

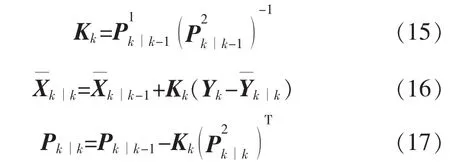
步骤4 设置迭代次数和目标误差，重复步骤1到步骤3，直至达到预设的目标误差或迭代次数，最终获得精确化后的状态向量，即未知节点的坐标（，）。

2 BP-UKF算法

所提出的BP-UKF算法，首先基于BP神经网络算法，将RSSI与距离之间的非线性关系通过训练已知数据信息进行逼近，进而估计待定位节点与锚节点间的物理距离，并在三边定位法的计算下获得待定位节点的初始坐标，随后利用无迹卡尔曼可以应用于非线性系统方程的特性，通过选取合适的迭代次数对坐标初始值进行精确化，以提高算法的定位精度。BP-UKF算法的流程如图4所示。

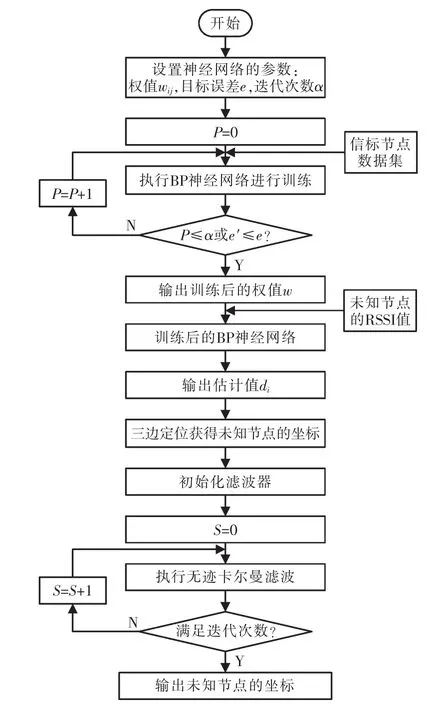
图4 BP-UKF算法流程Fig.4 BP-UKF algorithm flow chart

3 试验分析

3.1 试验设计

试验在宽敞的大厅中进行，由于存在障碍物，选取6 m×6 m的试验场地如图5所示。建立坐标系时取该区域的中心为原点，以便于计算。

图5 试验现场Fig.5 Experimental background

具体的试验步骤如下：

步骤1 在图5所示的试验场地中，分别放置4 个锚节点 AP1，AP2，AP3，AP4作为发射节点； 将可移动位置的接收节点放置在由锚节点围成的区域内，用于采集收发节点之间的RSSI。

步骤2 打开发射节点和接收节点，用上位机发送指令修改发射节点的本地时间，使4个发射节点实现时间同步；在上位机保存一段时间内收集到的RSSI值；移动接收节点在29个不同位置，并选取RSSI稳定后的200个RSSI值建立数据集，记RSSI数据集为，其中：i=1，2，…，200； j=1，2，…，29。

步骤3 对RSSI数据集进行均值滤波处理，作为 BP 神经网络的训练集， 记为 T=｛（Irss1，d1），（Irss2，d2），（Irss3，d3），（Irss4，d4）｝。

步骤 4 在区域内选取［X，Y］＝［-2，-1；-1，0］为待定位节点，将上位机接收到的Irss作为BP-UKF算法的输入值，并输出坐标估计值［，］及相应的坐标定位误差

步骤5 比较BP神经网络与传统的模型定位算法对非线性函数的拟合程度，选择距离估计误差MSEdis为判断依据并进行分析。

步骤6 为了验证精确化阶段UKF算法的定位精度优于扩展卡尔曼滤波EKF（extended Kalman filter），使用EKF算法对未知节点的初始坐标值进行优化，并获得估计坐标［X″，Y″］及相应的定位误差

3.2 数据分析

3.2.1 BP神经网络与传统定位算法的定位性能

在室内环境中RSSI易受到干扰、反射等外界因素的影响，并而影响定位性能。固定1个接收节点，移动发送节点，使发送节点和接收节点间距离的变化范围为1～18 m，移动间隔为1 m且在每个位置的采样次数为200，在均值滤波处理后绘制距离和带有噪声的Irss测量值之间的非线性函数关系。获得该环境下的路径损耗函数Irss=A-10nlgd的系数为A=-45，n=2.68，同时根据确定系数的路径损耗函数绘制出RSSE的理想值，如图6所示。

由图6可见，在室内环境下，RSSE测量值很容易受到环境的影响。直接使用传统的定位方法可能带来大的定位误差，且路径损耗函数的系数随着定位环境的改变而变化，需要进行实时更新。

BP神经网络与传统定位算法的定位误差见表1。分析可知，BP神经网络对Irss与距离之间非线性的拟合度，相较于传统的定位函数更精确，待定位节点的坐标估计更加可靠。

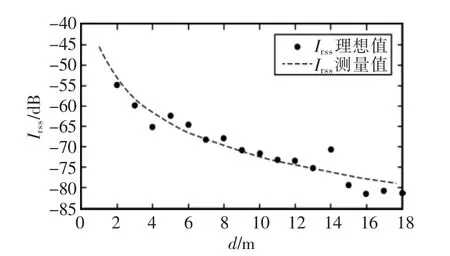
图6 室内定位性能分析Fig.6 Indoor positioning algorithm performance analysis

表1 两种算法的定位误差Tab.1 Positioning errors of the two algorithms

3.2.2 两种算法对未知节点坐标精确化的作用

取卡尔曼滤波器的状态估计误差协方差，测量噪声与过程噪声协方差的对角线元素分别为10-4，10-7，50。从算法运行的时间复杂度和定位误差两方面，分析BP-EKF与BP-UKF的性能。

（1）时间复杂度的不同

因为传感器节点的能量有限性，运行时间复杂度成为一个重要的衡量标准。对于BP-UKF和BPEKF算法，只需考虑EKF算法和UKF算法对初始坐标精确化过程的时间损耗。在不同的迭代次数下，2种定位算法所需时间如图7所示。

图7 不同迭代次数下EKF与UKF的运行时间Fig.7 Running time of EKF and UKF under different iterations

由图可见，随着迭代次数的增加，UKF和EKF 2种算法的运行时间都增加，但在相同的迭代次数下，UKF算法的运行时间明显小于EKF算法2个量级。所以，在时间损耗方面，UKF算法优于EKF算法。

（2）定位误差的分析

在不同的迭代次数下对EKF和UKF算法的精确化性能进行比较，仿真结果如图8所示。

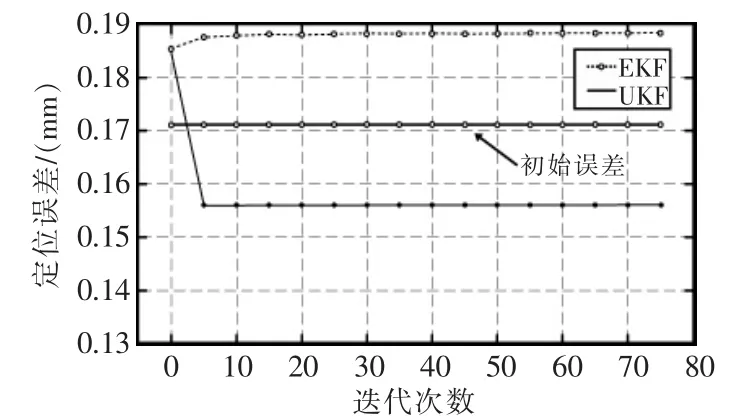
图8 不同迭代次数下算法的位置估计误差Fig.8 Position estimation error of algorithm under different iterations

图8 中，EKF和UKF 2种算法的定位误差分别为0.1561，0.1882；BP-EKF算法甚至增大了三边定位算法的初始估计误差；在迭代次数最大取10的情况下，BP-UKF算法便可很大程度地提高定位准确度。

3.2.3 坐标初始值对UKF算法定位精度的影响

为了更直观地分析BP-UKF算法中坐标初始值的选择对定位精度的影响，在10 m×10 m的区域内随机生成50个节点，并使用路径损耗函数获得噪声为5的RSSI数据集；取4个待定位节点，且未知节点的RSSI已知；状态估计误差协方差、测量噪声与过程噪声协方差取值为3，5，0.1；分别使用EKF和UKF，对该初始坐标进行精确化，与初始坐标为任意小值［0.1；0.1］作对比。大量试验表明，BP-UKF算法中使用三边定位法初始化坐标的方法，大大减少了滤波算法的迭代次数，更加验证了BP-UKF算法的有效性。

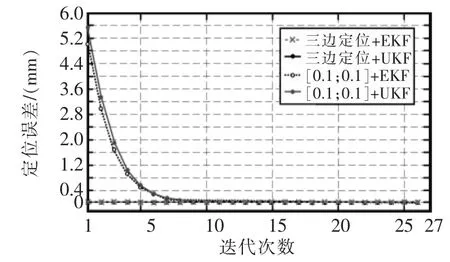
图9 不同初始坐标下EKF与UKF的定位误差Fig.9 Positioning error of EKF and UKF under different initial coordinates

由图 9 可见，设置［0.1；0.1］为坐标初始值，随着迭代次数的增加则算法的定位误差不断减小，充分体现了卡尔曼滤波算法的性能，且在迭代15次后才能达到与三边-KF算法同等的定位精度。经大量试验验证，当过程噪声协方差的取值不等于RSSI的噪声协方差时，为达到与三边-KF算法同等定位精度，［0.1；0.1］-KF算法需要的迭代次数远大于BP-UKF算法，很显然，BP-UKF算法中的坐标初始值的选择方法有较小的时间复杂度。

4 结语

文中提出BP-UKF定位算法，首先利用BP神经网络可以拟合任意非线性函数的特性，确定更加准确的Irss和距离之间的关系，进而通过量测的RSSI获得未知节点与锚节点间的距离，并用三边定位法估计未知节点的初始坐标，然后进一步采用无迹卡尔曼滤波算法对三边定位获得的坐标初始值进行精确化。BP-UKF算法一方面提高了对Irss与距离之间的非线性函数的拟合程度，对节点间距离的估计更加准确，另一方面选择无迹卡尔曼滤波对坐标的初始值进行精确化，降低了在扩展卡尔曼滤波中因为线性化导致的节点定位的估计偏差。同时，无迹卡尔曼滤波有较小的时间复杂度，适合应用到有限计算的无线传感器网络中。经过大量仿真试验验证了该算法的有效性。该算法具有一定的应用前景

参考文献：

[1] Qinghua L，Yu P，Junbao L，et al.RSSI-based localization through uncertain data mapping for wireless sensor network[J].IEEE SENSOR JOURNAL，2016，16（9）：3155-3162.

[2] Bensky A.Wireless positioning technologies and applications[J].Artech House，2016，9（6）：218-268.

[3] Malyavej V，Kumkeaw W，Aorpimai M.Indoor robot localization by RSSI/IMU sensor fusion[C]//Proc 10th Int Conf Electr Eng/Electron，Comput，Telecommun.Inf Technol，2013：1-6.

[4] YedavalliK，KrishnamachariB，RavulaS，etal.Ecolocation：a sequence based technique for RF localization in wireless sensor networks[C]//Proc Fourth Int Symp Information Processing in Sensor Networks.2005：1-8.

[5]Chen L-H，Wu E H-K，Jin M-H，et al.Homogeneous features utilization to address the device heterogeneity problem in fingerprint localization[J].IEEE Sensors J，2014，24（4），998-1005.

[6] Liu R，Sun K，Shen J.BP localization algorithm based on virtual nodes in wireless sensor networks[C]//6th International Conference on Wireless Communications Networking and Mobile Computing.2010：1-4.

[7] Yang Y，Zhao Y，Kyas M.A grid-scan maximum likelihood estimation with a bias function for indoor network localization[C]//International Conference on Indoor Positioning and Indoor Navigation.2014：1-9.

[8] Xiao Q，Xiao B，Bu K，et al.Iterative lo calization of wireless sensor networks：an accurate and robust approach[J].IEEE/ACM Trans Netw，2014，22（2）：608-621.

[9] Fang X，Jiang Z，Nan L，et al.Noise-aware localization algorithms for wireless sensor networks based on multidimensional scaling and adaptive Kalman filtering[J].Computer Communications，2017，101：57-68.

[10]Haykin S.神经网络原理[M].叶世伟，史忠植，译.北京：机械工业出版社，2004.

Indoor Localization Algorithm Based on BP-UKF for Wireless Sensor Network

HE Bin1，LV Xiao-jun2，ZHANG Chun-jia2，YANG Bo1
（1.School of Mathematical Sciences，Shanxi University，Taiyuan 030006，China；2.Institute of Computing Technologies，China Academy of Railway Sciences，Beijing 100081，China）

In order to solve the localization problem at the complex interior environment，indoor localization algorithm based on BP-UKF algorithm is proposed.This algorithm uses the BP neural network algorithm to obtain the relationship between the distance and Received Signal Strength Indication（RSSI） accurately by use of the characteristic in fitting any no-linear function.Then the distances between the unknown nodes and anchor nodes can be calculated.The coordinates of the nodes are initialized by using the trilateration with those distances.It uses the unscented kalman filter algorithm to deal non-linear system equation.The initial value of the coordinates of the positioning node is treated accurately by the estimated value of the distance as the observation variable.The result of simulation shows that BP-UKF algorithm can achieves reliable and accurate solution in interior environment than the traditional positioning algorithm.

indoor localization；BP neural network；trilateration；unscented kalman filter；non-linear function；wireless sensor network（WSN）

在室内定位研究中，基于接收信号强度指示[1]RSSI（received signal strength indication）的室内定位算法受到广泛的关注，但是基于RSSI的定位精度易受到多径效应、阴影衰落等影响[2]，使得室内定位技术向着更低能耗、更少实施成本、更好可测量性，以及更高定位精度等方向展开研究[3]。

TP183

A

1001-9944（2018）04-0071-05

10.19557/j.cnki.1001-9944.2018.04.017

2017-12-18；

2018-02-26

国家自然科学基金项目（U1334210，U1334210，61374059，61573230）

贺彬（1994—），女，硕士，研究方向为卡尔曼滤波、神经网络。