基于对流层散射的测向定位算法误差分析

王玉梅，张殿友，徐海洋(1.江苏科技大学，江苏 镇江 1003；.中国船舶重工集团公司第七二三研究所，江苏 扬州5101)

0 引 言

电磁波通过对流层散射可以传播到超出视距的范围，可以通过侦测对流层散射信号实现对运动辐射源的超视距侦察，若采用2个及以上的侦察站则可以实现超视距定位。目前，在利用对流层散射信号实现超视距定位的算法中，测向方位面定位算法[1]是一种快速高精度的超视距侦察定位算法。对于给定的定位体制，目标位置的求解算法不同，定位误差的大小也不同，并且由于参数测量误差的随机性，定位误差也是随机的[2]。因此需要对影响定位精度的因素[3-8]进行深入分析，从而采取措施克服不利条件，进一步提高定位精度。本文推导仿真了测向方位面定位算法的几何精度因子(GDOP)，并从目标距离、基线长度和测向精度这三个方面分析了对超视距定位误差的影响。

1 定位原理

1.1 椭球模型

目前，超视距信号传播普遍采用沿地球表面传播的轨迹模型。然而，地球是一个不规则的球体，实际中难以得到精确的集合模型，因此，往往采用某种近似球体，测向方位面定位算法采用WGS-84椭球模型[8]，曲率半径为：

(1)

式中：a为长半轴，a=6 378 137 m；b为短半轴,b=6 356 752.314 2 m；e为第一偏心率，e2=0.006 694 379 901 3。

大地坐标系和空间直角坐标系的转换关系为[9]：

(2)

式中：L为经度；B为纬度；H为高度。

1.2 测向方位面定位算法

利用对流层散射信号实现超视距定位，一般采用2个或2个以上的侦察站对散射信号进行截获并测向，利用测向交汇原理对远方辐射源进行定位。测向方位面定位算法的定位示意图如图1所示。

考虑2个侦察站、1个辐射源情况，假设目标和侦察站位于地球表面。已知2个侦察站的地理坐标为S1(L1,B1)、S2(L2,B2)，设目标所在位置的地理坐标为T(Lt,Bt)，Az1、Az2为两侦察站S1、S2测得的目标T的方位角。

图1 测向方位面交叉定位示意图

首先得出2个测量坐标系下的测向方位面方程，然后将2个方位面方程先转换到空间直角坐标系下并与椭球面方程连列，最后将连列的方程组转换到大地坐标系下，通过化简计算直接得出目标经纬度。式(3)给出了目标经纬度的最终计算结果(具体推导过程见参考文献[1])：

(3)

式中：Az1≠kπ；Az2≠kπ，k=0,1；能计算的目标位置范围为Lt∈(-90°,90°)，Bt∈(-90°,90°)；其他范围这里不做讨论。

值得注意的是，该定位算法计算得出的只有目标的经纬度，没有给出目标的高度，而是默认目标位于参考椭球的表面。但该算法计算过程中也不需要侦察站位置的高度信息，即侦察站高度对该算法没有影响。

2 定位误差分析

定位误差主要与定位体制以及相应的定位算法和相应的参数测量误差有关。对于无源侦察定位系统定位误差的描述和度量有许多方法[10]，在工程中通常采用圆概率误差(CEP)、几何精度因子(GDOP)来衡量定位精度。定位误差的几何精度因子用下式表示[9]：

(4)

通常将GDOP表示成一定区域内的等高线图，使得目标的定位精度表示更加直观，可以将其作为定位系统侦察站布站的参考。

2.1 几何精度因子推导

由于测向方位面定位算法采用经纬度进行计算，因此对式(2)两边微分，可以得到用经纬度表示的几何精度因子：

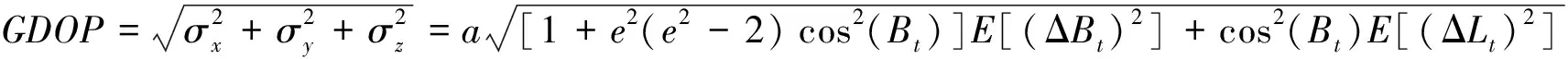
(5)

式中：E[(ΔLt)2]和E[(ΔBt)2]通过下面的式(7)和式(8)进行求解。将式(3)两边微分可得：

(6)

(7)

(8)

为了表述简便，令：

N=-cotAz1cosB2sinL1+cosB2sinB1cosL1+cotAz2cosB1sinL2-cosB1sinB2cosL2；

D=-cotAz1cosB2cosL1-cosB2sinB1sinL1+cotAz2cosB1cosL2+cosB1sinB2sinL2；

M=cotAz1sin(Lt-L1)+sinB1cos(Lt-L1)。

则式(7)和式(8)中：

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

2.2 定位精度仿真分析

2个侦察站位于图中“*”所示的位置，基线中点位于(20°,10°)处，辐射源目标在经度范围为10°～30°、纬度范围为0°～20°的栅格内，两侦察站测向精度、站址误差均相同。测向方位面定位算法GDOP分布图如图2～图5所示，相应参数见图上标注。

图2 测向方位面交叉定位算法GDOP分布图(L=100 km，测向精度1°，站址误差5 m)

图3 测向方位面交叉定位算法GDOP分布图(L=100 km，测向精度0.5°，站址误差5 m)

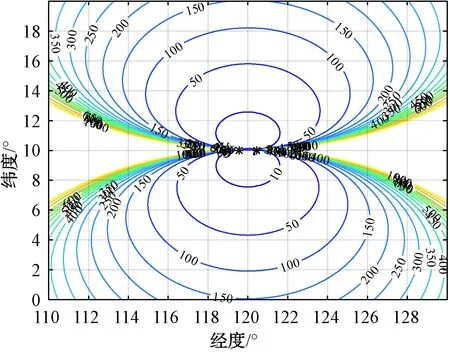
图4 测向方位面交叉定位算法GDOP分布图(L=100 km，测向精度0.5°，站址误差20 m)

图5 测向方位面交叉定位算法GDOP分布图(L=50 km，测向精度0.5°，站址误差20 m)

比较图2～图5得到如下结论：

(1) 根据图2～图5，目标到侦察站的距离越远，定位误差越大并且目标逐渐偏离两侦察站基线的中垂线时定位误差逐渐增大。

(2) 比较图2和图3，其他条件相同的情况下，相较于测向精度为1°时，测向精度为0.5°的定位精度几何分布的等值线更稀疏。这表明在同样的条件下，提高测向精度能够获得更高的定位精度。

(3) 比较图3和图4，其他条件相同的情况下，站址误差从5 m增大到20 m后GDOP的等值线分布基本不变。若侦察站站址采用GPS进行定位，而一般情况下军用GPS定位精度达到0.3 m，因此，通常情况下侦察站站址误差引起的定位误差非常小，可以忽略不计。

(4) 比较图4和图5，其他条件相同的情况下，基线长度L=100 km比L=50 km时的精度几何分布的等值线明显更加稀疏，这表明增大基线长度能够提高定位精度。

2.3 几种影响定位精度的因素分析

根据2.2节的分析，发现目标距离、测向精度和基线长度对定位精度的影响较大，而站址误差对定位精度的影响很小。因此以下在不同场景下就目标距离、测向精度和基线长度对该算法定位精度的影响情况作出更加具体的分析。

首先设定典型场景，如图6所示，辐射源目标T1从(-20°,10°)向北运动(经度不变，纬度增大)，辐射源目标T2、T3分别从与T1关于经线L1、L2对称的点向北运动，对应T1、T2、T3的场景分别表示为场景1、场景2和场景3。场景1和场景2中的距离d1、d2为目标到侦察站S1的球面距离，场景3中的距离d3是指辐射源目标到侦察站S2的球面距离。由于T2、T3关于T1对称，那么当T1、T2、T3位于相同纬度上时，d1=d2=d3。

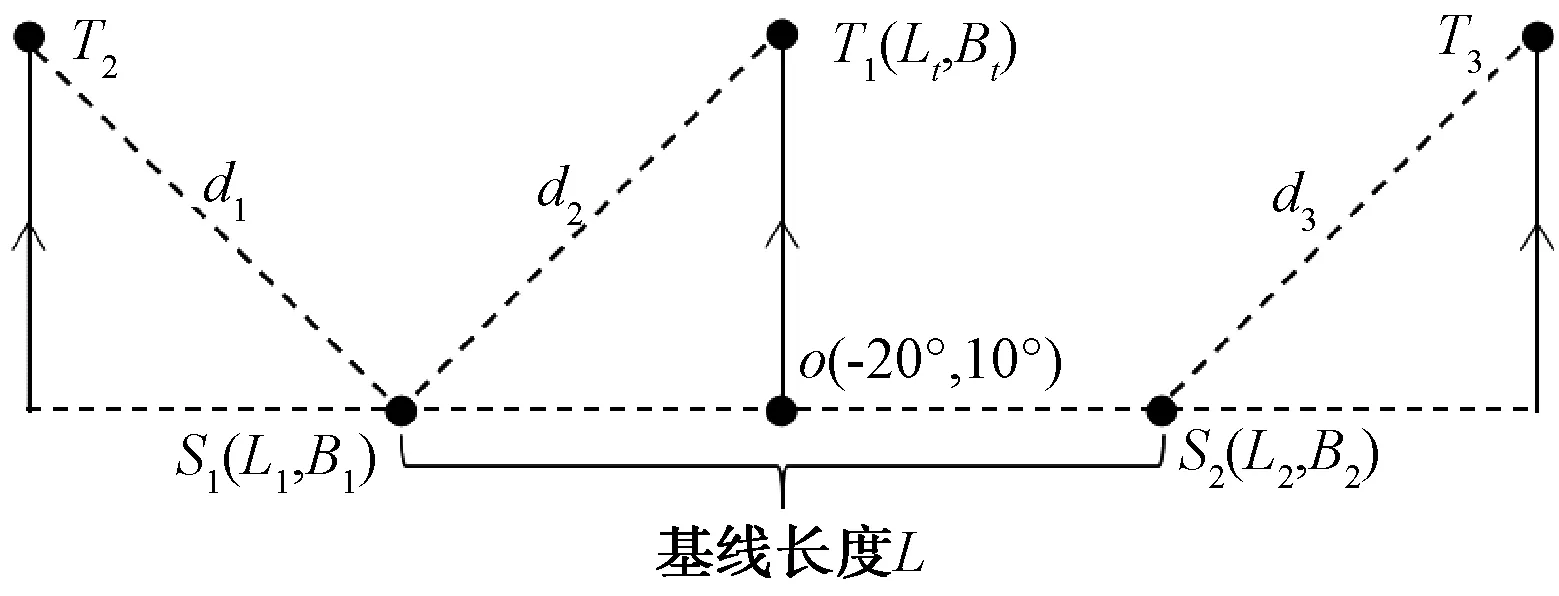
图6 目标与侦察站布站示意图

2.3.1 目标距离及测向精度对定位误差的影响

按照场景1、场景2和场景3进行布站，测向精度取2°、1.5°、1°和0.5°进行仿真计算，结果如图7～图10所示。

图7 测向方位面交叉定位算法误差分布(L=200 km，测向精度2°，站址误差20 m)

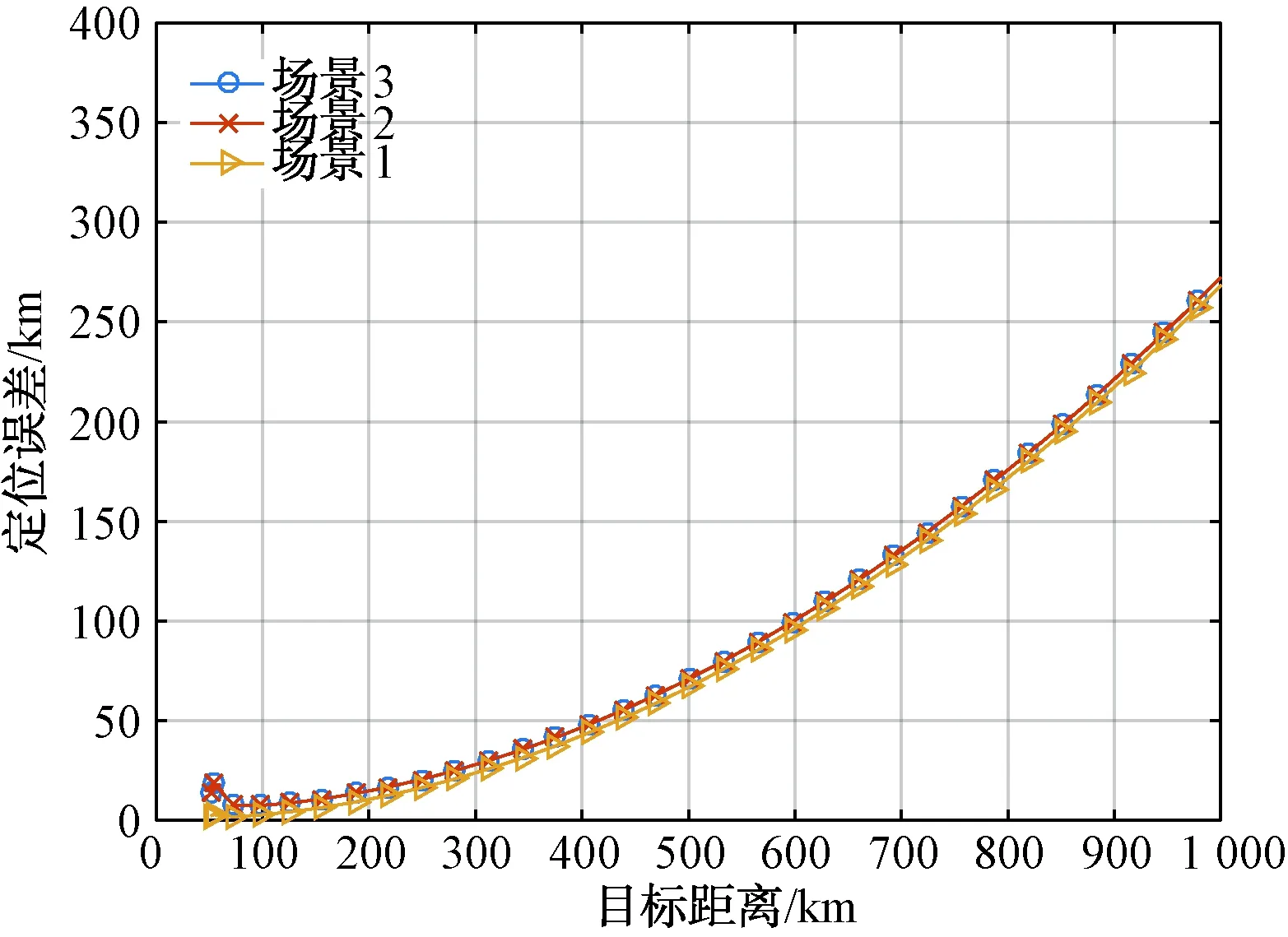
图8 测向方位面交叉定位算法误差分布(L=200 km，测向精度1.5°，站址误差20 m)

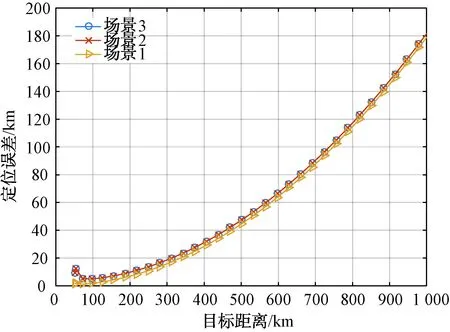
图9 测向方位面交叉定位算法误差分布(L=100 km，测向精度1°，站址误差20 m)

图10 测向方位面交叉定位算法误差分布(L=200 km，测向精度0.1°，站址误差20 m)

根据图7～图10，得出如下结论：

(1) 其余条件相同时，场景1(目标与侦察站呈等腰三角形分布)的定位误差小于场景2和场景3，这说明在布站时尽量使得目标位于两侦察站基线中垂线上能够减小定位误差。

(2) 随着测向精度的提高，定位精度显著改善，因此采取措施提高侦察站的测向精度对于提高整个系统的定位精度将起到非常关键的作用。

(3) 随着目标距离的增大，定位误差先快速减小而后增大，即并不是目标距离越近定位误差就越小，而是存在某一目标距离使定位误差最小，当目标距离小于最小值点时，定位误差反而快速增大。取步长为0.000 5 rad(约为0.028 6°)，计算得到不同测向精度下(L=100 km，站址误差20 m)取得误差最小值的目标的距离，在场景1下，不同测向精度下均在目标距离约为126.92 km时取得最小值，而场景2和场景3在目标距离约为165.90 km时取得最小值，这个计算得到的数据结果表明取得最小值点的目标距离与测向精度无关。

2.3.2 基线长度对定位误差的影响

按照场景1、场景2和场景3进行布站，基线长度L分别取20 km、30 km、50 km、100 km进行仿真计算，结果如图11～图14所示。取步长为0.000 5 rad(约为0.028 6°)，计算得到不同基线长度下取得误差最小值的目标距离，计算结果见表1与图15。

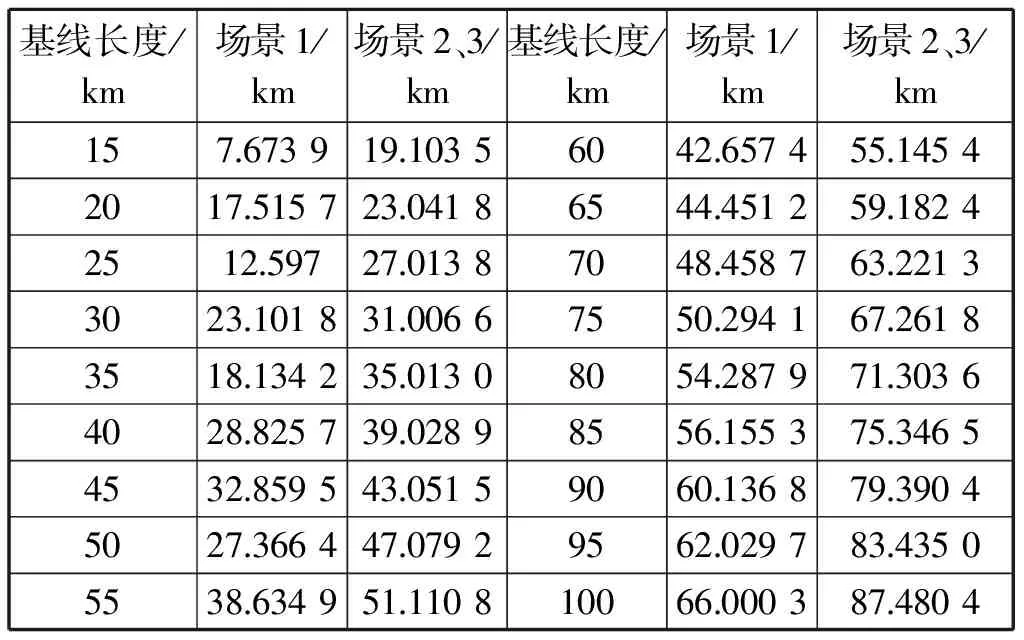
表1 最小值点的目标距离与基线长度关系表(测向精度0.5°，站址误差20 m)

比较图11～图14，其他条件相同的情况下，增加基线长度，定位误差改善明显。因此为了减小定位误差，可以根据实际情况，考虑站间通信等问题，在侦察站布站时尽量增加基线长度。

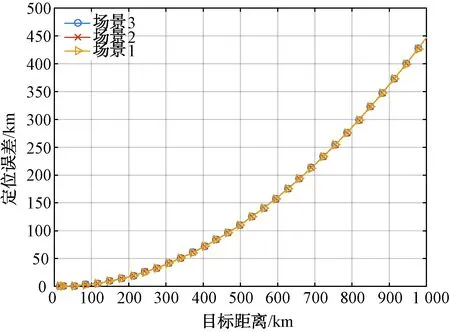
图11 测向方位面交叉定位算法误差分布(L=20 km，测向精度0.5°，站址误差20 m)

图12 测向方位面交叉定位算法误差分布(L=30 km，测向精度0.5°，站址误差20 m)

图13 测向方位面交叉定位算法误差分布(L=50 km，测向精度0.5°，站址误差20 m)

图14 测向方位面交叉定位算法误差分布(L=100 km，测向精度0.5°，站址误差20 m)

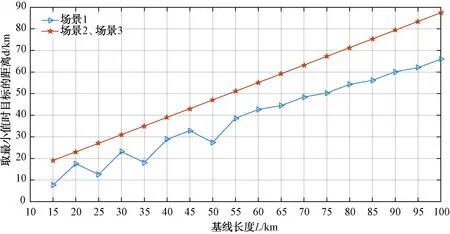
图15 最小值点的目标距离与基线长度关系图(测向精度0.5°，站址误差20 m)

根据表1和图15，场景2和场景3下取得最小值的目标距离与基线长度呈正比例增加。场景1下，基线长度超过50 km后取得最小值的目标距离与基线长度也基本呈正比。即在其它条件相同的情况下，当目标到侦察站的方位角为某一定值时可以得到最小的定位误差。

3 结束语

提高测向方位面定位算法定位精度的关键在于提高测向精度以及尽可能增大基线长度。对于采用何种测向方法对对流层散射信号进行测向、如何提高测向方法的测向精度以及实际应用过程中基线长度能达到的最大取值等问题还可以进一步分析。另外，本文只对两站定位系统的定位误差做了分析，若采用多个侦察站同时进行侦察定位，还可以从多站量测数据的关联、融合算法以及多站布站情况等方面进行研究。

[1] 高轶,王玉梅,徐海洋.一种对流层散射信号快速高精度无源定位算法[J].舰船电子对抗,2017(4):50-54.

[2] 田中成,刘聪锋.无源定位技术[M].北京：国防工业出版社，2015.

[3] 何缓,杨春山,傅文斌.无源雷达定位精度分析[J].现代雷达,2007，29(5):1-3.

[4] 罗争.双站测向交叉定位算法精度分析[J].科技传播,2016(19):230-231.

[5] 谢鑫.测向交叉定位最优布站方案分析[J].电子科技,2014(8):85-89.

[6] 朱剑辉,方洋旺,张平,李望西.双机协同定位误差分析的研究[J].电光与控制,2012,19(6):21-25.

[7] 曹鑫,陈欣.无源测向交叉定位的误差分析与校正[J].雷达与对抗,2011,31(3):1-4.

[8] 朱永文,娄寿春,韩小斌.双基地雷达测向交叉定位算法的误差模型[J].火力与指挥控制,2007(6):51-53.

[9] 施一民.现代大地控制测量[M].北京:测绘出版社,2008.

[10] 王本才,王国宏,何友.多站纯方位无源定位算法研究进展[J].电光与控制,2012(5):56-62.