环锭数码纺粗纱喂入位置对混色纱表面显色的影响

郭明瑞， 杨瑞华， 周 建， 薛 元， 高卫东

(生态纺织教育部重点实验室(江南大学), 江苏 无锡 214122)

色纺纱是采用有色纤维混合纺制而成的纱线。目前，色纺纱大都采用多种有色纤维通过前纺混合纺制而成[1-2]。三通道环锭纺数码纺纱技术[3]是一种采用有色粗纱在细纱工序混合纺制色纺纱的新技术。该技术采用并列组合式后罗拉和组合式后皮辊代替原有的后罗拉及后皮辊，实现了并列组合式后罗拉的3个通道独立驱动，在1个细纱锭位输入 3根不同颜色的粗纱，经过相同或不同倍率的牵伸然后横向汇聚成纱，可生产出混纺比在一定范围内变化的混纺纱，称为混色纱。混色纱具有独特的外观，给人一种幻彩、朦胧的艺术效果，可广泛应用于各种针织、机织面料和服装。

基于环锭纺成纱原理，对于Z捻或S捻纱线，纤维在加捻三角区的横向位置对其在成纱中的内外分布有显著影响[4-6]，这就导致混色纱表面各组分的分布面积比例与粗纱喂入比例并不等价。为准确纺制一定颜色比例的混色纱，研究粗纱喂入位置对混色纱表面各组分显色比例的影响具有重要意义。计算机技术在大数据彩色图像处理方面有不可比拟的优势[7-8]，图像处理技术已经初步应用到色纺纱领域[9]。

环锭纱纤维内外转移的研究重点主要集中在纺制包芯纱的工艺，包括单粗纱喂入、双粗纱喂入纺制包芯纱。研究发现前罗拉钳口输出须条的宽度对成纱纤维内外转移有明显影响。较窄的输出须条不利于边缘纤维包覆，扁平状的输出须条有利于边缘纤维分布在纱线表面[10-12]。输出位置对纤维在纱线内外转移分布规律的研究较少。

本文提出了一种测量环锭数码纺混色纱表面三组分纤维分布面积比的方法，研究了粗纱喂入比确定的条件下，粗纱喂入位置对混色纱表面各组分显色比例的影响。为简化问题，降低图像多色彩处理的复杂程度，增加数据处理的准确性，采用同定量的黑、白两色涤纶粗纱为原料，按等比例喂入1根白色粗纱、2根黑色粗纱纺制混色纱，改变白色粗纱的喂入位置，纺制白/黑/黑、黑/白/黑、黑/黑/白 3种混色纱，初步探讨3根粗纱等比例喂入时粗纱喂入位置对成纱表面纤维显色比的影响。

1 三色粗纱输入混色纱纺纱原理

图1示出三色混色纱，是由三通道环锭数码纺纱技术纺制而成，在纺纱工艺对传统环锭纺纱机的牵伸机构进行了改进设计。图2示出三通道环锭数码纺粗纱喂入位置示意图。采用并列组合式后罗拉，构成3个相互独立的后牵伸区，实现3根粗纱独立牵伸，通过改变各后牵伸区的牵伸倍率，在一定范围内调整各通道粗纱的喂入量，进而控制成纱中各粗纱的混纺比例。3根不同颜色的粗纱通过3眼喇叭口喂入对应通道的罗拉钳口，再通过后牵伸区集合器改变两侧通道的粗纱行进方向，在中罗拉后钳口将三色粗纱汇聚，经过前牵伸区同步牵伸纺制成纱。

图1 三色混色纱Fig.1 Three-color melange yarn

图2 三通道环锭数码纺粗纱喂入位置示意图Fig.2 Diagram of roving feeding location of three-channel digital ring spinning

图3为三通道环锭数码纺制混色纱加捻示意图。加捻过程中由前罗拉钳口输出的纤维加捻成纱，将纤维以一定角度引向斜下方，这样从前罗拉钳口输出的纤维在前罗拉表面有一段包围弧，这时纤维与前罗拉表面有接触，而与前皮辊无接触，所以在加捻过程中，加捻三角区平面上方与下方受力不一致，导致加捻过程中三角区左、右位置纤维受力不平衡，进而影响加捻三角区形态，使其不能保持理想的等腰三角形。同时，加捻三角区不同位置纤维所走路径也不一致，纤维会产生不同的几何转移。这些综合因素导致加捻三角区不同位置的纤维分布于纱线表面的比例不一致。

图3 混色纱加捻示意图Fig.3 Diagram of twisting of melange yarn

2 图像采集与处理

2.1 图像采集

混色纱的直径大都在百微米级，人眼对这个尺度范围的纱线表面直接观察，很难分辨出各色纤维的面积分布，必须借助显微镜放大几十倍至数百倍观察，但随着放大倍数的增大，观察到的视野范围变小，同一视野内显示的纱线面积不能有效涵盖混色纱表面的混色周期，并且混色纱表面纤维的分布比较复杂，人工很难对其表面各色纤维分布面积进行统计。本文在具有水平方向图像拼接功能的彩色数码显微镜上加装纱线卷绕装置，每次卷绕固定长度，在一定放大倍率条件下，通过图像拼接，采集一定卷绕长度的纱线图像。同时，光照环境对标准图像采集具有明显影响，本系统放置于无窗封闭空间，以减弱外部光照的影响，维持采集环境光照稳定，提高图像数据的稳定性。

图像采集系统如图4所示，包括电脑、显微镜、载物台、张力装置、绕纱辊、电动机、可编程逻辑控制器(PLC)。其中：载物台为电动载物台，能水平方向移动，实现图像水平方向拼接；载物台上固定有纱线张力装置，绕纱辊由步进电动机驱动，PLC控制步进电动机运行，通过设置脉冲数量实现纱线定长卷绕，每次卷绕由人工点动。

图4 图像采集系统Fig.4 Image acquisition system

图5为纱线采集区域示意图。纱线采集区两侧的张力装置可保证被采集的纱线张紧程度基本一致，呈平直状态，将采集区左侧边缘设置为起始位置，在1个图像采集拼接过程中，电动载物台左移，直至拍摄到设定的采集区右侧边缘，然后载物台自动返回起始位置，手动点击纱线卷绕按钮，卷绕装置执行纱线卷绕动作，1次卷绕长度近似等于1次采集拼接图像中纱线的长度。

图5 纱线采集区域示意图Fig.5 Diagram of yarn image capturing

各组分纤维在纱线内外的分布主要受粗纱喂入位置，即纤维在加捻三角区的横向位置决定，与纤维颜色并无相关性，由于黑、白两色在色彩空间中距离最远，图像数据区分度大，为简化问题，增加数据处理的准确性，本文采用相同定量的黑、白两色涤纶粗纱纤维(线密度为1.33 dtex、长度为38 mm)为原料，按比例喂入1根白色、2根黑色粗纱纺制混色纱。

以白色粗纱为示踪对象，将黑白混色纱放置在黑色载物台上采集纱线图像，在一定光照条件、聚焦深度下，黑色纤维颜色与载物台背景颜色接近，可以视为同一类颜色，而白色纤维在黑色背景下清晰呈现。图6为黑白混色纱显微镜拼接图像。

图6 黑白混色纱显微镜拼接图像Fig.6 Mosaic image of black/white mélange yarn

2.2 图像处理

2.2.1RGB色彩数据

数码图像的单元是像素点，本文目的是将图像中白色和黑色2类像素点进行分类，分割出白色、黑色像素点的数量，白色像素点的个数对应纱线表面白色纤维所占面积。数码彩色图像中每个像素点的色彩采用RGB色彩空间，色彩信息由红色R、绿色G、蓝色B3个通道组合而成。图7为1张黑白混色纱显微镜拼接图像各像素点在RGB颜色空间的分布图。虽然选取了对比度较大的黑、白两色，但是由于光的衍射现象，黑、白两色的交界区域所表现的颜色会介于两色之间。由图可知，黑白混色纱图像中所有像素点呈连续状分布于RGB颜色空间，而RGB颜色空间是非均匀颜色空间，在非均匀颜色空间中，空间不同区域等距离的2点颜色相差并不相等，这种颜色的非线性变化不利于颜色的分类，同时，三维空间中2类数据分界面的确定问题比较复杂，因此，需要对RGB色彩进行进一步转化处理，以保证计算结果的准确性。

2.2.2RGB向CIEL*a*b*颜色空间的转换

本文将图像的RGB数据转换至CIEL*a*b*均匀颜色空间，在CIEL*a*b*颜色空间中：L*表示明度；a*、b*表示色品。图8为图7中纱线图像各像素点在CIEL*a*b*颜色空间中的分布图。为便于计算机处理数据，图中的L*、a*、b*值经过线性变换，均为正值。

图7 黑白混色纱图像像素点RGB颜色空间分布图Fig.7 Distribution diagram of image of black/white melange yarn in RGB color space

图8 黑白混色纱图像像素点在CIE L*a*b*颜色空间分布图Fig.8 Distribution diagram of image of black/white melange yarn in CIE L*a*b* color space

由图8可知，像素点在CIE L*a*b*颜色空间中的分布主要分为2类：一类像素点的L*较小，沿a*-b*平面呈扁平状分布；另一类像素点在较小范围的a*、b*值区域内，沿L*成柱状分布。所以L*值，即明度，可以作为区分2类数据的参数。

2.2.3分界点确定

本文选取像素点的L*值作为分类参数。由于黑白混色纱显微镜采集图像中黑色区域面积大，白色区域面积小，并且数量相差较大，采用MatLab对图像进行处理，选取L*值绘制像素点分布频数直方图，图9为L*值(0～240)的像素点分布频数直方图。可知随着L*值增大，像素点的数量总体有减少趋势。

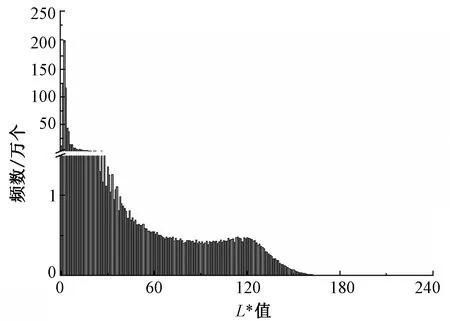
图9 像素点L*值分布频数直方图(0≤L*≤240)Fig.9 Frequency histogram of L* of pixels (0≤L*≤240)

本文选取不同的阈值，对图像进行处理，将黑、白2类数据分割，然后将分割后的图像进行二值化，再将二值化图像与原图进行人工比对，确定较优的分界点，经过多次人工比对发现当L*=60时，图像分割比较理想，所以此次采样选定分界点L*的值为60。图10示出黑白混色纱原图以及L*分界点为60的二值图。

图10 黑白混色纱原图及二值图Fig.10 Image of black/white melange yarn (a) and binaried image in demarcation L*=60 (b)

2.2.4采样数量确定方法

随机变量的均值大小仅依赖于随机变量的分布，当随机变量的概率分布确定以后，这个随机变量的均值就是确定的常数。本文研究的黑白混色纱，在粗纱牵伸过程中，纤维的变速点是随机的，所以沿纱线长度方向纤维的分布可以认为是一个随机变量[13-14]。沿纱线长度方向连续采集相同大小的图像，每张图像统计出的白色像素点个数可以看作一个随机变量，所以这个随机变量的均值应为常数。对纱线进行连续的图像采集，采用MatLab对每张图片中白色像素点的数量进行统计，然后计算随着采样数量增加白色像素点的平均值，随着采样数量的增加白色像素点的平均值趋于某一定值，则认为采样数量可以代表整体情况。

2.2.5显色比计算方法

将某一喂入位置的粗纱在成纱表面分布的纤维面积占纱线表面总面积的百分比称为显色比Ki。由于一定长度上纱线径向纤维分布是等概率的，所以，通过从单侧拍摄纱线的外观图片，用MatLab软件提取图片中白色纤维区域的像素点个数，分别提取 3个不同喂入位置成纱图像中白色纤维像素点数量Pi，并以单侧纱线的显色比作为成纱的显色比。显色比Ki的计算式如下：

(1)

式中，n为粗纱喂入位置的数量。

3 实 验

纺纱实验在JWF1551型三通道环锭数码纺纱机上进行，采用定量为460 g/(10 m)的黑、白两色涤纶粗纱，白色粗纱分别按喂入质量比为33.33∶33.33∶33.33，从左、中、右喂入位置纺制19.6 tex的Z捻与S捻黑白混色纱，涤纶纤维线密度均为 1.33 dtex，长度均为38 mm。

纱线图像采集在密闭无窗黑屋中进行，采样用基恩士VHX-5000型显微镜，配备VHX-S550E型电动载物台，光源采用环形光源，光源亮度级别为4级(可选0～255级)，放大倍率为100，单张拼接图像采集纱线长度为25 mm，每个品种纱线采集图像300张，选取分割点L*值范围为55～65。

将纺制的纱线用16 G宏成HC21 K型纬编圆机织造纬平针织物，线圈长度为0.6 mm，横向密度为98列/(10 cm)，纵向密度为160行/(10 cm)。

采用DataColor 650型分光测色仪对各纱线对应的织物测色，选取30 mm大孔径，100%紫外线(滤镜关闭)，D65光源，10°视场，每个样品测试6个位置，取平均值。

4 结果与分析

4.1 混色纱显色比例结果

表1示出不同分割阈值(55≤L*≤65)条件下图像法获得的各混色纱的显色比结果。图11示出19.6 tex等比例Z捻与S捻黑白混色纱在L*=60时，白色粗纱在不同喂入位置的单张图像纱线表面，白色纤维所占像素点数量的平均值随取样数量增加的变化趋势。

表1 显色比结果Tab.1 Results of color proportion

图11 纱线白色纤维像素点数量平均值(L*=60)Fig.11 Average pixels of white fiber (L*=60)(a) Z twist yarn; (b) S twist yarn

4.2 混色纱织物颜色测量结果

本文采用Datacolor 650型分光测色仪对黑白混色纱织物进行测色，以验证图像法获得混色纱的可靠性。表2示出3种黑白混色纱织物的L*测量值。

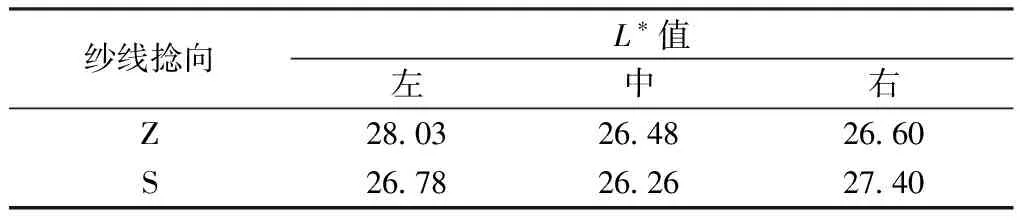
表2 黑白混色纱织物L*测量值Tab.2 Test results L* values of black/white yarn fabrics

4.3 结果分析

由表1可知，由于在55≤L*≤65的阈值范围内，阈值变化对不同图像中白色像素点的数量变化影响比例一致，对最终显色比结果影响不明显。说明采用图像法获取的显色比结果在一定范围内受分割阈值的影响不明显，结果稳定性好。

为了了解参保人员的基本情况，笔者随机走访了几个村进行实地调研，发放调查问卷120份，调查对象为男性70人，女性50人，年龄段主要集中在31-59岁，占调查总人数的91.7%；60岁以上的10人。受教育情况为，小学及以下、初中和高中的人数分别为61人、47人和12人。经济来源情况：纯务农的63人，这部分人员月均收入均在1000元以下；手工艺者27人，月均收入约在2000—4000元，经商者12人，依靠子女供养的18人。

经过人工比对，本文选取L*=60为最优分割阈值，由图11可知，在300张采样数量的条件下，对图像进行处理所得出的白色像素点平均值已经趋于稳定，因此，采用此数据计算出的显色比结果可以代表总体水平。

表1结果显示：阈值L*=60时，对于纺制Z捻纱线，粗纱从左、中、右喂入，其分布于细纱表面的显色比分别为36.84%、30.95%、32.21%，左侧通道显色比最高，中间通道显色比最低，右侧通道略高于中间通道；对于纺制S捻纱线，粗纱从左、中、右喂入，其分布于细纱表面的显色比分别为32.09%、31.00%、36.91%，右侧通道显色比最高，中间通道显色比最低，左侧通道略高于中间通道。结果表明：纤维在加捻三角区的横向位置对其分布在纱线表面的比例有明显影响，并与捻向有关。

白色纤维占纱线表面比例越高对应的纱线明度也越高，反之，纱线明度越低。由表2可知：Z捻混色纱织物，白色粗纱从左侧喂入，对应织物的L*值最大，为28.03，从中间喂入，对应织物的L*值最小，为26.48；S捻混色纱织物，白色粗纱从右侧喂入，对应织物的L*值最大，为27.40，从中间喂入，对应织物的L*值最小，为26.26。

由以上结果可知：本文利用图像法获取的纱线表面显色比与分光测试仪的测试结果是一致的。对于三通道环锭纺技术纺制等比例Z捻混色纱，左侧通道显色比最高，中间通道显色比最低；纺制S捻混色纱，右侧通道显色比最高，中间通道显色比最低。

5 结 论

采用三通道环锭数码纺技术纺制白、黑、黑3股粗纱等比例的19.6 tex Z捻涤纶混色纱，通过图像法研究白色粗纱分别在左、中、右喂入位置时白色纤维在混色纱的表面显色比，结果为 36.84%、30.95%、32.21%，可知：对于Z捻混色纱，左侧通道显色比最高，中间通道显色比最低; S捻涤纶混色纱表面显色比为32.09%、31.00%、36.91%，可知右侧通道显色比最高，中间通道显色比最低。该结论与纱线外观所反映的颜色效果一致。

本文提出的图像法给出了环锭数码纺成纱过程中粗纱喂入位置对混色纱外观显色比例的量化影响关系，同时也为准确测量此类混色纱各组分纤维在纱线表面分布面积提供了有效手段，为实际生产中所需特定色彩的混纺比工艺设计提供了参考依据。弥补了此类混色纱评价仅依靠人主观评价，或利用测色仪对其色彩进行宏观评价的不足。

FZXB

参考文献：

[1] 桂亚夫. 浅谈色彩艺术与色纺技术[J]. 棉纺织技术, 2015, 43(8):77-80.

[2] 黄玉强, 于文菡, 潘璟, 等. 新型色纺混色工艺流程的研究与应用[J]. 棉纺织技术, 2014, 42(3):46-49.

HUANG Yuqiang, YU Wenhan, PAN Jing, et al. Research and application of new colored spinning processing flow[J]. Cotton Textile Technology, 2014, 42(3):46-49.

[3] 高卫东, 郭明瑞, 薛元, 等. 基于环锭纺的数码纺纱方法[J]. 纺织学报, 2016, 37(7):44-48.

GAO Weidong, GUO Mingrui, XUE Yuan, et al. Digital spinning method developed from ring spinning[J]. Journal of Textile Research, 2016, 37(7):44-48.

[4] HUA Tao, TAO Xiaoming, CHENG Kwok Po Stephen, et al. Effect of geometry of ring spinning triangle on yarn torque: part I: analysis of fiber tension distribution[J]. Textile Research Journal, 2007, 77(11):853-863.

[5] HUA Tao, TAO Xiaoming, CHENG Kwok Po Stephen, et al. Effects of geometry of ring spinning triangle on yarn torque: part II: distribution of fiber tension within a yarn and its effects on yarn residual torque[J]. Textile Research Journal, 2010, 80(2):116-123.

[6] WEI Li, HUANG Suping, ZHU Ting, et al. Research on shape of spinning triangles in the ring spinning system[J]. The Journal of the Textile Institute, 2016, 107(4):420-430.

[7] 刘成龙. 精通MatLab图像处理[M]. 北京:清华大学出版社, 2015:48-71.

LIU Chenglong. Proficient in MatLab image processing[M]. Beijing: Tsinghua University Press, 2015:48-71.

[8] 费峥峰, 赵雁南. 一种快速彩色图像颜色分割算法[J]. 微计算机信息, 2007, 23(29):185-187.

FEI Zhengfeng, ZHAO Yannan. A fast color segmentation algorithm[J]. Microcomputer Information, 2007, 23(29):185-187.

[9] 沈利利, 李忠健, 潘如如, 等. 色纺纱线中纤维混色比例的图像检测[J]. 纺织学报, 2016, 37(3):

138-143.

SHEN Lili, LI Zhongjian, PAN Ruru, et al. Image inspection of fiber blending percentages in colored spun yarns[J]. Journal of Textile Research, 2016, 37(3):138-143.

[10] 梁蓉, 林建华. 传统和赛络纺锦纶长丝包芯纱的比较[J]. 纺织学报, 2006, 27(8):85-88.

LIANG Rong, LIN Jianhua. Comparison of traditional and siro polyamide filament core-spun yarns[J]. Journal of Textile Research, 2006, 27(8):85-88.

[11] 闫海江. 两种包芯纱的工艺优选及质量对比[J]. 棉纺织技术, 2015, 43(1):37-40, 82.

YAN Haijiang. Process optimization and quality comparison of two kinds of core-spun yarn[J]. Cotton Textile Technology, 2015, 43(1):37-40, 82.

[12] 吴汉林, 王继红, 赵今平, 等. 特细号精梳棉氨纶包芯纱的生产[J]. 棉纺织技术, 2012, 40(4):40-42.

WU Hanlin, WANG Jihong, ZHAO Jinping, et al. Production of superfine combed cotton spandex core spun yarn[J]. Cotton Textile Technology, 2012, 40(4):40-42.

[13] 于伟东, 储才元. 纺织物理[M]. 2版. 上海:东华大学出版社, 2009:281-306.

YU Weidong, CHU Caiyuan. Textile Physics[M]. 2nd ed. Shanghai: Donghua University Press, 2009:281-306.

[14] 张文赓. 罗拉牵伸原理[M]. 上海:东华大学出版社, 2011:53-61.

ZHANG Wengeng. Theory of Roller Drafting[M]. Shanghai: Donghua University Press, 2011:53-61.