基于功率调节的IWSN实时可靠路由研究*
吴 平,孙子文,2*
(1.江南大学物联网工程学院,江苏 无锡 214122;2.物联网技术应用教育部工程研究中心,江苏 无锡 214122)
工业无线传感器网络IWSN(Industrial Wireless Sensor Networks)[1-2]的路由协议应当满足3个主要目标:实时性,以最小延迟传送数据包到目的地;可靠性,以最小误差传送数据包到目的地;网络寿命,以最小能耗传送数据包到目的地。但是,工业环境的特点使得这3个主要目标受到威胁。第一,在工业生产流程中,系统需要快速地对厂内生产设备以及生产环境的状态做出响应,与WSN相比,工业环境中的无线通信对数据的时延有非常高的要求[3];第二,在数据传输中遇到空洞时即意味着数据包转发无法到达目的地,这将导致网络进入故障状态,因此如何遏制空洞以提高可靠性就显得非常重要;第三,工业无线传感器网络中的无线节点具有诸如电源受限等的资源约束,其中路由是电源消耗的主要因素,因此选择合适的能量策略是提高网络寿命的关键[4]。
研究人员已研究了多种提高IWSN网络可靠性或网络寿命的路由策略。在文献[5]中,采用地理路由协议GPSR(Greedy Perimeter Stateless Routing),它运用贪婪转发模式转发数据包,当遇到空洞时采用周边转发模式转发数据包,使得转发可靠性增加,但却加大了端到端延迟。在文献[6]中,采用了一种基于GRSR的GRSR-1路由算法,该算法提出两种度量值:贪婪度量值和边界度量值。在度量值中综合考虑了距离、角度和密度因素,最终降低了端到端延迟和截止期错失率,但是该算法没有考虑能量因素,并且在遇到空洞时,该算法使用的周边转发模式会使得节点跳数增多,导致实时性变弱。在文献[7]中,采用了一种能量优化的地理路由协议。该协议通过在优化函数中加入地理位置信息和剩余能量信息,保证了数据包的正确传输并且优化了能量,但是由于协议在遇到空洞时依然使用的是周边转发模式,因此实时性能受到威胁。在文献[8]中,采用了一种基于两跳邻居节点信息的地理路由算法—Greedy-2算法,该算法依靠两跳距离信息使数据包及时避开空洞,可靠性增加,但Greedy-2的边缘恢复机制无法保证截止期交付率,实时性受到威胁。这些协议虽然一定程度上提高了可靠性以及网络寿命,但却忽略了实时性,因此还存在不足。
研究人员也研究了很多提高IWSN实时性以及网络寿命的路由策略。在文献[9]中,采用了基于双跳速度的路由协议THVR THVR(Two-Hop Velocity-based Routing)。路由协议通过两跳的“望远镜”功能,具有提前感知能力;以速度代替距离,实时性得到增强;并通过考虑剩余能量,平衡了能量消耗,但THVR使用的概率丢包策略不能有效解决空洞问题,可靠性不能得到保证。在文献[10]中,提出了一种基于两跳速度信息的梯度路由,结果显示实时性能和能量效率提高,但是算法本身计算复杂度较高,另外协议在面对空洞时并没有给出具体的可靠性措施。这些协议都通过不同的方法提高了实时性以及网络寿命,但对于可靠性要求高的IWSN,这些方法也存在不足。
针对IWSN对实时性、可靠性以及网络寿命的要求,文献[11]采用了基于功率调节的实时路由协议CDRR(Critical Data Real-Time Routing)。CDRR路由协议在截止期的基础上选择速度最快的转发节点来满足实时性;通过选择剩余能量较多的节点来提高网络寿命;通过功率调节来满足节点的可靠性。虽然CDRR全面考虑了实时性、可靠性以及节点能耗,但其一跳速度策略并没有明显提高实时性,并且只考虑剩余能量也不足以平衡网络能量,有必要寻求综合性能更好的路由协议来满足IWSN的3个目标。
本文针对工业无线传感器网络对实时性、可靠性以及网络寿命的要求,研究了一种基于两跳速度的实时可靠路由算法THTR(Two-Hop Reliable and Real-Time Routing)。一方面,节点通过收集两跳范围内节点的位置与速度信息,来降低截止期丢包率,提高实时性;另一方面,通过调整传输功率,每个传感器节点动态选择其传输距离,提高协议的可靠性;此外,通过权重将剩余能量以及节点转发能耗同时考虑,平衡了网络能量,提高了网络寿命。
1 基于功率调节的实时可靠路由协议
从实时性、可靠性以及能量消耗3个方面进行路由协议的研究。
1.1 基于两跳速度的实时路由策略
所提出的路由算法通过将距离除以估计的延迟,把满足端到端延迟的问题转化为提供每跳所需速率的局部问题,以实现期望的及时性数据包传递。文献[9]仿真结果表明,通过定义基于两跳的速度,可以优化跳数,降低截止期错失率,提高能量有效性;但文献[12]也指出,从两跳到三跳的复杂度明显上升,端到端延迟也大幅度提高。因此,基于两跳速度的策略是对性能改进和复杂度之间的折中。
1.1.1 传输延迟估计
链路的延迟估计对路由决策有着很大影响。链路延迟由传播延迟和传输延迟两部分组成,将数据包从节点传给目的节点路径中的跳邻居节点定义为。传输的总延迟为:
delay1=delaysp(i,i+1)+delaydata(i,i+1)
(1)
delay2=delaysp(i+1,i+2)+delaydata(i+1,i+2)
(2)
式中:delay1是将数据包从节点i节点传到i+1节点的总延迟时间,delay2是将数据包从i+1传到i+2的总延迟时间;delaysp(i,i+1)是节点i和i+1之间的传播延迟,delaysp(i+1,i+2)是节点i+1和i+2之间的传播延迟;delaydata(i,i+1)是节点i和i+1之间的数据传输延迟;delaydata(i+1,i+2)是节点i+1和i+2之间的数据传输延迟,数据传输延迟的值是固定的,可以由数据包长度除以数据包传输的比特率得到。
基于自由空间模型给出接收/发射功率之比[13],如式(3):
qi+1_rec/qi_send=[λ/(4πr)]2
(3)
式中:qi_send是转发节点i的发射功率,qi+1_rec是邻居节点i+1的接收功率,λ是信号的波长,r是节点i与节点i+1之间的距离。由式(3)可得两节点间的距离,如式(4):
(4)
于是节点i和i+1之间的传播延迟估计为:
(5)
式中:f是电磁波的频率,c为电磁波的传播速度,满足c=λf。
1.1.2 路由机制
设源节点S到目的节点D的距离为d(S,D),截止时间为tdeadline,那么所需的源节点S到目的节点D的数据包的传输速度[14]为:
(6)
为了计算转发节点i与两跳邻居节点之间的速度,给出集合式(7)和式(8):
H1(i+1)={i+1|d(i,D)-d(i+1,D)>0,i+1∈W(i)}
(7)
H2(i+2)={i+2|d(i+1,D)-d(i+2,D)>0,
i+1∈H(i+1),i+2∈W(i+1)}
(8)
式中:H1(i+1)表示所有满足条件的一跳邻居节点i+1集合,W(i)和W(i+1)表示节点i或节点i+1传输范围内的所有节点;表示所有满足条件的两条邻居节点i+2集合。
一跳和两跳节点转发示意图如图1所示。

图1 节点转发示意图
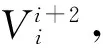
(9)
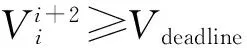
(10)
在路由机制中,邻居表由节点ID、节点位置以及剩余能量构成。其中,节点ID表示节点身份,位置表示地理坐标。通过两轮HELLO消息,每个节点都知道它的一跳或两跳邻居个数和位置。
1.1.3 关节度量
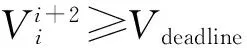
(11)
式中:E(qi_send)表示以qi_send为发射功率转发数据包消耗的能量,E(qi+1_send)表示以qi+1_send为发射功率转发数据包消耗的能量。Ei+1为节点i+1的剩余能量,Ei+2表示节点i+2的剩余能量。
采用文献[15]给出的能量策略来估计节点转发数据包所要消耗的能量,如式(12)所示:
(12)
式中:Eelec表示发射电路损耗的能量。若传输距离小于阈值d0,功率放大损耗采用自由空间模型;当传输距离大于等于阈值d0时,采用多路径衰减模型。εfs、εamp分别为这两种模型中功率放大所需的能量,l表示数据包的比特数[16]。
同时定义如下的线性优化函数:
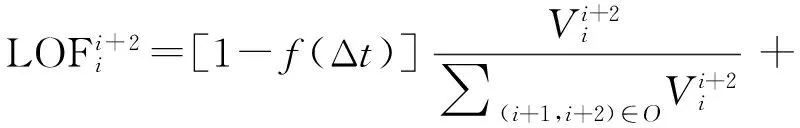
(13)
(14)
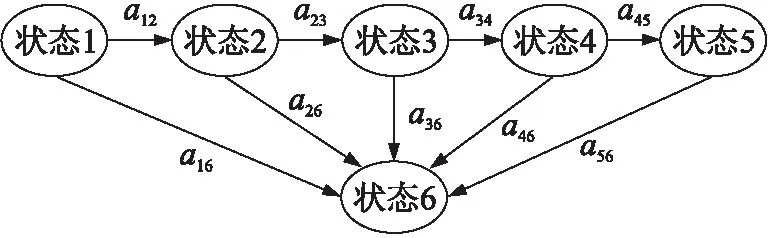
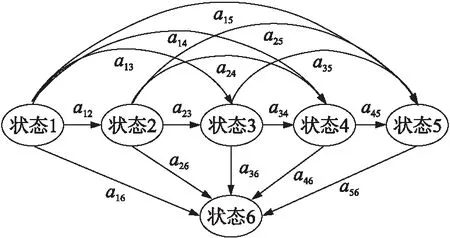
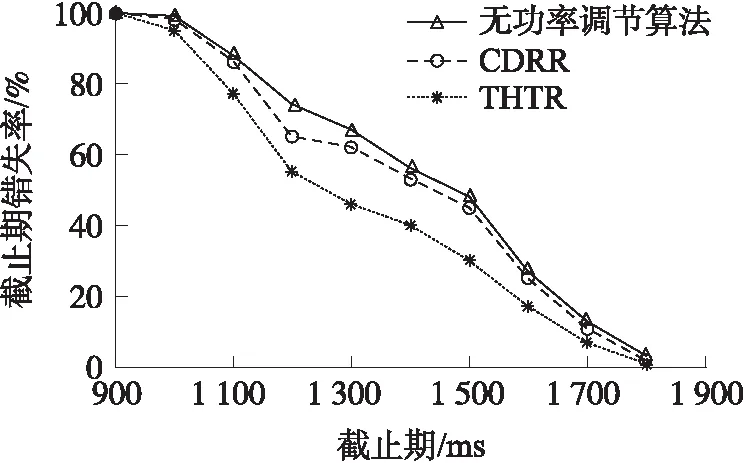
式中:0 通过分析,当截止时间较长、剩余时间Δt较多或者剩余距离较小时,对于前者速度的权重就小,由此可以更多地将业务分配到剩余能量较多或者消耗能量较少的节点;当截止时间较短、剩余时间Δt较少或者剩余距离较大时,需要保证截止期传输成功率,对于前者速度的权重就大。 IWSN的整体系统可靠性取决于传感器节点,通信链路以及网关的可靠性。其中,传感器节点的可靠性对提高系统可靠性起着重要作用。 基于两跳速度的路由协议能够很大程度上能改善实时性能,但地理路由一般遵循贪婪转发模式,这种转发模式的一个明显的缺陷就是遇到空洞,即通信范围内没有满足速度的可用的转发节点或者是集合H1(i+1)=∅,传统方法是启动重新路由机制或启用周边转发模式重新寻找路径,但是这样的方式不能及时地提供数据。针对以上问题,本文给出以下解决策略: ①尽力转发机制 在转发节点i的通讯范围内有满足式(7)但不满足速度要求的一跳邻居节点,即集合H1(i+1)≠∅。 定义如下优化度量函数: (15) 式中:0<β<1是加权因子,d(i+1,D)表示一跳邻居节点到目的节点的距离。为了简化描述,将前者的比值定义为距离因素,后者的比值定义为剩余能量因素,可以利用权值系数来体现不同的环境对两种因素的影响程度。 得到优化函数值后,选择最优路径进行转发,将该解决策略定义为尽力转发策略。 ②功率调节机制 在转发节点i的通讯范围内没有满足式(7)也没有满足速度要求的一跳邻居节点,即H1(i+1)=∅。 在这种情况下,为了能够可靠地传输数据包,加入功率调节机制解决这种空洞问题。首先,转发节点正常工作时都是以0 dBm的发射功率转发数据包,当H1(i+1)=∅时,转发节点将切换到下一功率级E1以便寻找更佳路径,如果再次发生故障,转发节点再次切换功率,直到切换至E3。当切换至E3后依然无法路由,转发节点将进入故障状态。 为了分析与对比加入功率调节机制和未加入功率调节机制的协议的可靠性,引入状态转移模型。图2是节点没有使用功率调节的协议状态转移模型。状态转移模型中全部使用固定节点。其中,状态1为源节点,状态2至状态4为中间节点,状态5为目的节点,状态6为遇到空洞后的故障状态。a12、a23、a34和a45分别表示节点之间正常传输的状态转移概率,a16、a26、a36、a46和a56分别表示节点在前5个状态进入故障的状态转移概率。在这种情况下,由于没有功率调节,节点进入故障状态的可能性非常大,可靠性无法得到保证。 图2 无功率调节的状态模型 图3 带功率调节的状态模型 图3是带功率调节机制的THTR状态转移模型。每个传感器节点具有4个功率级0 dBm、1 dBm、2 dBm 和4 dBm,也就是说,每个传感器节点可以基于允许的功率动态地选择其传输距离。a12、a23、a34和a45表示0 dBm的状态转移概率,a13、a24、a35表示 1 dBm 的状态转移概率,a14和a25表示2 dBm的状态转移概率,而a15表示4 dBm的状态转移概率。节点无论是在5个状态中的哪一个状态都有可能遭遇空洞陷入故障状态,此状态用状态6表示。 根据图3的状态模型,给出状态跃概率矩阵A[17],如式(16): (16) 式中:a11=a12+a13+a14+a15+a16,a22=a23+a24+a25+a26,a33=a34+a35+a36,a44=a45+a46。 令pk(t)=p(qt=k)表示节点在t时刻处于状态k的概率,根据切普曼-柯尔莫哥洛夫微分方程,有 p′(t)=p(t)A (17) 式中:p(t)=[p1(t)p2(t)p3(t)p4(t)p5(t)]为状态向量,p′(t)为p(t)的一阶微分状态向量。对式(17)进行Laplace变换,得: (18) 若节点在初始条件下处于正常状态,那么 p(0)= (19) 接着,将状态跃居概率矩阵A转置的值代入式(18)中,对P(s)进行Laplace反变换,最终得到节点在t时刻处于状态k的概率pi(t)(i=1,2,3,4,5)。令R(t)为系统的总可靠度,那么, R(t)=1-p6(t)=p1(t)+p2(t)+p3(t)+p4(t)+p5(t) (20) 若式(7)是∅,则对转发节点i启用功率调节机制并重新选择路径,直至调节至最大发射功率E3,若依然无法找到合适的路径,节点将进入故障状态。具体流程如图4所示。 图4 THTR算法节点转发数据包流程图 为研究算法的有效性,本文对THTR路由算法进行了仿真实验,并将THTR路由算法与已有的未加入功率调节机制的协议、CDRR算法的性能进行了对比。 利用MATLAB R2012b进行可靠性仿真。对图2中无功率调节算法的状态转移模型进行可靠性评估,并且将它与图3中THTR的状态转移模型可靠性进行对比。考虑传输范围、节点个数的影响,将图2中成功和故障状态转换概率都设定为0.02(0 dBm的传输距离大约在30 m~40 m,假设传输范围内有50个节点,转移概率大约为0.02),并代入式(16)得到概率矩阵A,将矩阵A的转置以及式(19)代入式(18)中,得到节点在t时刻处于状态k的概率pi(t)(i=1,2,3,4,5),最终根据式(20)得到总可靠度。同理,对于图3中的成功和故障状态转移概率,都设定为0.002(假设4 dBm的传输范围内有500个节点,那么转移概率大约为0.002),并根据上述方法得到总可靠度。 图5的结果表明,随着天数的增加,网络可靠度都在减小,对于无功率调节算法,在时间趋于300天时网络可靠度急剧下滑,在300天时变为0;对于加入功率调节机制的THTR,在时间趋于800天时可靠度开始下滑,并在800天时变为0。因此,通过对模型的分析,加入功率调节机制可以增加网络的可靠性。 图5 总可靠度 图6 网络拓扑图 采用OPNET建模者14.5建立实时性与能耗仿真平台。在200 m×200 m的区域内随机部署200个节点,源节点位于(175 m,175 m),目的节点位于(20 m,20 m)。图6显示了网络的拓扑结构。在OPNET上进行仿真的节点参数配置如表1所示。 表1 场景及节点参数配置 在模拟中,每个节点都以恒定比特率来转发和接收数据包。节点的初始发射功率设定为0 dBm,遇到空洞后,陆续切换至1 dBm、2 dBm和4 dBm。 为了强调实时性,式(15)中的参数β设置为较大值0.9。根据文献[18]得出的实验结果,对式(12)的未知参数进行设置,最终实验仿真参数如表2所示。 表2 实验仿真参数 以初始的场景及节点参数为基础,对3种协议的性能在不同的截止期需求(900 ms~1 800 ms)条件下进行仿真对比。每一个截止期进行10次模拟,将单次模拟时间设置为45 min,采用10次模拟结果的平均值。为了提供节点故障的行为,给定80个节点以20 s的间隔陆续关闭,并且对网络节点的邻居表以20 s的间隔进行更新。 图7 截止期错失率 2.2.1 截止期错失率 截止期错失率DMR(Deadlines Missed Ratio)是实时性数据传递的重要性能参数。表示在最后期限内没有成功传递至目的节点的数据包与发送数据包个数的比值。图7显示了在不同截止期的3种路由协议的DMR。从图7可以看出,THTR在任意一个截止期下的DMR都比无功率调节算法和CDRR都要小。截止期为1 300 ms时,THTR的DMR为46.2%,CDRR为62.3%,相差了16.1%;截止期为1 500 ms时,THTR为30.2%,CDRR为45%,相差了15.2%。相比CDRR,THTR的主要优势在于THTR采用了基于两跳速度的路由机制,而两跳相对于一跳不仅优化了跳数,并且有一定的可能性提早发现路由空洞而避免它[13]。而对于无功率调节算法,数据包的丢失率相对于THTR和CDRR都比较大(无功率调节算法在搜索不到邻居时数据包将丢失),因此截止期错失率在各个截止期就会比较大(在1 300 ms,无功率调节算法的DMR为67%,相对于THTR,错失率差异最大,达到21%),但是另一方面,较于CDRR而言,由于采用了两跳机制,虽然截止期错失率还是较高,但两者差异表现的并不是太大(在1 200 ms,无功率调节算法的DMR为74.2%,CDRR的DMR为64.9%,差异最大,为9.3%,不超过10%)。 当源节点设定个数在2~16,截止期设定为 1 500 ms时,3种路由协议的截止期错失率比较如图8所示。 图8 不同源节点个数下的截止期错失率 图8显示随着源节点的增多,截止期错失率也在不断增加。这是因为源节点的增多使得待传数据包增多,网络负载增大,可能导致网络拥塞以及信道冲突。此外,从图8可以看出THTR算法在不同源节点个数的情况下截止期错失率要比无功率调节算法和CDRR小很多,实时性能较好(当源节点为2时,THTR的DMR为33.9%,相对于DMR为51%的无功率调节算法和DMR为47.6%的CDRR,错失率差异最小,分别为17.1%和13.7%)。一方面是由于两跳速度策略降低了截止期错失率,另一方面,网络拥塞的存在会增加由于数据重传次数增多而带来的延迟,而功率调节机制的引入减少了丢包率,在一定程度上减少网络拥塞带来的负面影响,从而增加链路稳定性。 2.2.2 能量消耗 对THTR算法、无功率调节算法和CDRR算法进行能耗有效性对比。首先评估在每个截止期下从源节点到目的节点成功传递的数据包能耗的平均值,再分别取10次模拟结果的平均值作为实验结果进行对比。图7中,考虑到当截止期为900 ms时,3种路由协议的截止期错失率都为100%,于是在对能量消耗进行评估时将不再考虑900 ms时的包平均能耗。 图9中,当截止期在1 000 ms到1 400 ms之间,THTR的包平均能耗比CDRR的包平均能耗都低10%以上,特别是截止期在1 100 ms时,THTR的包平均能耗为102 mJ,比包平均能耗为117 mJ的CDRR少了15 mJ,表明THTR比CDRR更加节能。这是因为THTR采用两跳策略优化了跳数,降低了截止期错失率以及采用了不同的能量策略,CDRR仅仅考虑了节点的剩余能量,而THTR不仅考虑了剩余能量还考虑了转发数据包所需要的能耗。此外,从图9可以看出,截止期在1 000 ms和1 300 ms之间时,无功率调节算法的包平均能耗总是比THTR的包平均能耗低6%~9%,截止期在1 400 ms到1 800 ms之间时,两者包平均能耗基本相差不大,这是因为无功率调节算法的截止期错失率较高,而仿真只计算了成功传递的数据包的平均能耗,相对于加了功率调节机制的THTR,无功率调节算法的包平均能耗较小。 图9 平均能耗比较 本文通过把功率调节机制加入到两跳速度的路由策略中,研究了一种实时可靠的路由协议。首先,通过对状态转移模型的分析,可靠性得到提升,网络寿命随之增强;其次,两跳速度策略有效地降低了数据包的截止期错失率,从而降低了传输延迟,提高了实时性;最后,采用新的能量策略,既考虑了节点的剩余能量也考虑了节点转发数据包能耗,平衡了网络能量,提高了网络寿命。 参考文献: [1] 郑涛. 工业无线传感器网络MAC协议研究[D]. 北京:北京交通大学,2014:1-135. [2] Sheng Z,Mahapatra C,Zhu C,et al. Recent Advances in Industrial Wireless Sensor Networks toward Efficient Management in IoT[J]. IEEE Access,2015,3(10):622-637. [3] Vehbi C Gungor,Gerhard P Hancke. Industrial Wireless Sensor Networks:C-Hallenges,Design Principles,and Technical Approaches[J]. IEEE Transactions on Industrial Electronics,2009,56(10):4258-4265. [4] Tiab A,Bouallouche-Medjkoune L. Routing in Industrial Wireless Sensor Networks:A Survey[R]. Chinese Journal of Engineering,2014:1-7. [5] 张威,施伟斌. 无线传感器网络GPSR路由协议研究[J]. 电子测量技术,2010,33(9):118-121. [6] 孙磊,张和伟,冯铁军,等. 一种贪婪地理路由协议的改进算法[J]. 现代电子技术,2016,39(11):16-20. [7] Soltani M R,Motamedi S A,Ahmadi S,et al. Power-Aware and Void-Avoidant Routing Protocol for Reliable Industrial Wireless Sensor Networks[J]. International Conference on Wireless Communications,2011,237(3):1-5. [8] 王建新,赵湘宁,刘辉宇.一种基于两跳邻居信息的贪婪地理路由算法[J]. 电子学报,2008,36(10):1903-1909. [9] Li Y,Chen C S,Song Y Q,et al. Enhancing Real-Time Delivery in Wireless Sensor Networks with Two-Hop Information[J]. IEEE Transactions on Industrial Informatics,2009,5(2):113-122. [10] Quang P T A,Kim D S. Enhancing Real-Time Delivery of Gradient Routingfor Industrial Wireless Sensor Networks[J]. IEEE Transactions on Industrial Informatics,2012,8(1):61-68. [11] Kumar M,Tripathi R,Tiwari S. Critical Data Real-Time Routing in Industral Wireless Sensor Networks[J]. IET Wireless Sensor Systems,2016,6(4):144-150. [12] Chen C S,Li Y,Song Y Q. An Exploration of Geographic Routing withk-Hop Based Searching in Wireless Sensor Networks[C]//International Conference on Communications and Networking in China,2008:376-381. [13] 张新生. 自由空间传播模型[DB/OL]. https://baike.baidu.com/item/自由空间传播模型,2015-01-17. [14] He T,Stankovic J A,Lu C,et al. A Spatiotemporal Communication Protocol for Wireless Sensor Networks[J]. IEEE Transactions on Parallel and Distributed Systems,2005,16(10):995-1006. [15] Heinzelman W R,Chandrakasan A,Balakrishnan H. Energy-Efficient Communication Protocol for Wireless Microsensor Networks[J]. Hawaii International Conference on System Sciences,2000:3005-3014. [16] 龙胜春,卢定乾,池凯凯. 基于同构传感器网络的能量空洞避免策略[J]. 传感技术学报,2016,29(1):103-108. [17] 吴军,邵新宇,邓超. 隐马尔科夫链模型在装备运行可靠性预测中的应用[J]. 中国机械工程,2010,21(19):2345-2349. [18] 陈敏. OPNET物联网仿真[M]. 武汉:华中科技大学出版社,2015:156-159.1.2 可靠实时路由

[p1(0)p2(0)p3(0)p4(0)p5(0)]T=
[10000]T1.3 THTR算法流程


2 仿真实验与结果分析
2.1 可靠性分析


2.2 实时性与能耗分析




3 结束语

