重力向下延拓的迭代法对比分析研究

吴姿颖， 邓居智， 王彦国， 罗 潇， 王 娥

(1. 东华理工大学 放射性地质与勘探技术国防重点学科实验室，南昌 330013； 2. 广东省核工业地质局 二九三大队，广州 510800)

0 引言

向下延拓是位场数据处理及反演解释的重要手段，它能够突出浅部地质异常，划分水平叠加异常。但向下延拓是典型的不适定问题，直接使用会导致计算结果出现明显的不稳定现象，通常采用添加低通滤波器的方法来提高向下延拓稳定性。在改善向下延拓稳定性方法中，正则化法[1-2]、Wiener滤波法[3]、匹配组合滤波法[4]、泰勒级数展开法[5]及广义逆算法[6]等在一定程度上提高了计算稳定性，但向下延拓深度有限。徐世浙[7]提出的积分迭代法实现了大跨度向下延拓，之后各种不同模式的迭代法应运而生，如泰勒级数迭代法[8]、导数迭代法[9]、相关系数法[10]、补偿延拓法[11]、迭代维纳滤波法[12]。学者们还针对空间域积分迭代法计算效率低的问题，将积分迭代法引入到了波数域中，实现了快速计算[13]；针对积分迭代法压制高频干扰不足问题还提出了一系列改进措施[14-15]；针对泰勒级数迭代法迭代次数少的优点和高频干扰压制能力不足问题，提出了正则-积分迭代法[16]。

虽然迭代法在解决向下延拓上的良好应用效果已被普遍认同，但不同迭代模式之间关联性及差异性，尤其不同迭代模式的应用效果，需要进行深入研究与分析，以便选择更为适合的迭代模式进行有效的向下延拓。基于此，笔者对常用的积分迭代法、泰勒级数迭代法和补偿向下延拓法这三种方法进行了理论模拟和应用实例的对比研究，总结典型迭代法的适用性。

1 基本原理

在波数域中，向下延拓可以表示为式(1)。

UB=UAψ

(1)

其中:UA、UB分别为观测面和延拓面的位场波谱；ψ=exp(wz)为理论向下延拓算子；z为向下延拓深度；w为圆波数。由于向下延拓是不适定问题，直接使用理论延拓因子会导致计算不稳定性。在解决这一问题上，目前普遍认为迭代法具有较好的应用效果。这里选取了常用的积分迭代法、泰勒级数迭代法和补偿向下延拓法三种方法进行对比研究分析，以评判不同迭代模式的应用效果。

1.1 积分迭代法

积分迭代法是由徐世浙院士[7]在空间域中提出的，刘东甲等[13]将其引入到了波数域中，并严格证明了迭代法的收敛性。该方法是将原平面位场值作为延拓面初值，再将原平面位场值与延拓面上初值向上延拓到原平面结果之差作为剩余值对延拓面位场值进行修正，采用逐次循环迭代实现的，该方法的波数域迭代递推公式为：

(2)

其中:φ=exp(-wz)为向上延拓算子，利用数学归纳法可得到积分迭代法的通式为式(3)。

(1-φ)+1]=

UAψ[1-(1-φ)n+1]

(3)

1.2 泰勒级数迭代法

泰勒级数迭代法是将波数域中的向下延拓算子进行泰勒级数展开，取前N项和代替向下延拓理论算子进行近似向下延拓，并采用迭代法进行逐步逼近得到的，其迭代公式为式(4)。

(4)

(5)

1.3 补偿向下延拓法

补偿法是基于侯重初[17]的补偿圆滑滤波和陈生昌等[6]提出的广义逆算法推导出来的，其补偿向下延拓的迭代公式为式(6)。

(6)

(7)

从式(3)、式(5)、式(7)可以看出，迭代事实上是在理论延拓算子上添加了一个与迭代次数有关的低通滤波器，只是不同迭代法出发点不同。另外，积分迭代法、泰勒级数迭代法和补偿向下延拓法的迭代通式具有很强的相似性，不同之处在于通式中向上延拓因子φ之前所使用的初始滤波算子不同，积分迭代法是“1”，为全通滤波器；泰勒级数迭代法的是φ，为高通滤波器；而补偿法的是HD，为中低通滤波器。

1.4 滤波特性

图1是积分迭代法、泰勒级数迭代法和补偿向下延拓法这三种方法的滤波特性曲线，可以看出，理论下延算子随着波数的增加呈现指数型放大，而三种迭代法的滤波因子对高频成分均有一定的压制，但积分迭代法和泰勒级数迭代法的响应算子仍是高通滤波，对高频干扰仍有放大作用。补偿法的滤波因子则在中低频段更能较好地逼近理论延拓因子，在高频段则更有效地压制高频成分，即补偿法在低频段能更精确地逼近理论下延因子而对高频成分则更有效地压制。因此，补偿法在理论上具有更高的计算精度和计算稳定性，笔者认为根本原因在于迭代法使用的初始滤波器不同。

图1 不同迭代法的滤波特性Fig.1 Filter characteristics of different iterative methods

2 模型试算

为验证积分迭代法、泰勒级数迭代法和补偿向下延拓法的有效性，构建了由四个不同参数球体组成的叠加模型，各个模型体相对位置见图2，模型体A、B、C、D中心坐标分别为(10，10，1.5)、(20，10，6)、(10，20，6)和(20，20，4)，半径分别为0.5 km、2.5 km、2 km、1 km，四个模型体剩余密度均为0.5 g/cm3，并在组合模型产生的重力数据上添加了0.5%随机噪声(图2)，数据网格点距为0.1 km。从图2可以看出，受叠加异常影响，模型体A、B上方的重力极值与模型体中心位置不对应，模型体D上方的重力异常则是以等值线扭曲为标志，难以从原始异常图中精确识别出地质体的位置。为了提高异常分辨率，对原始含噪异常采用三种迭代法进行了向下延拓10倍、20倍点距计算。

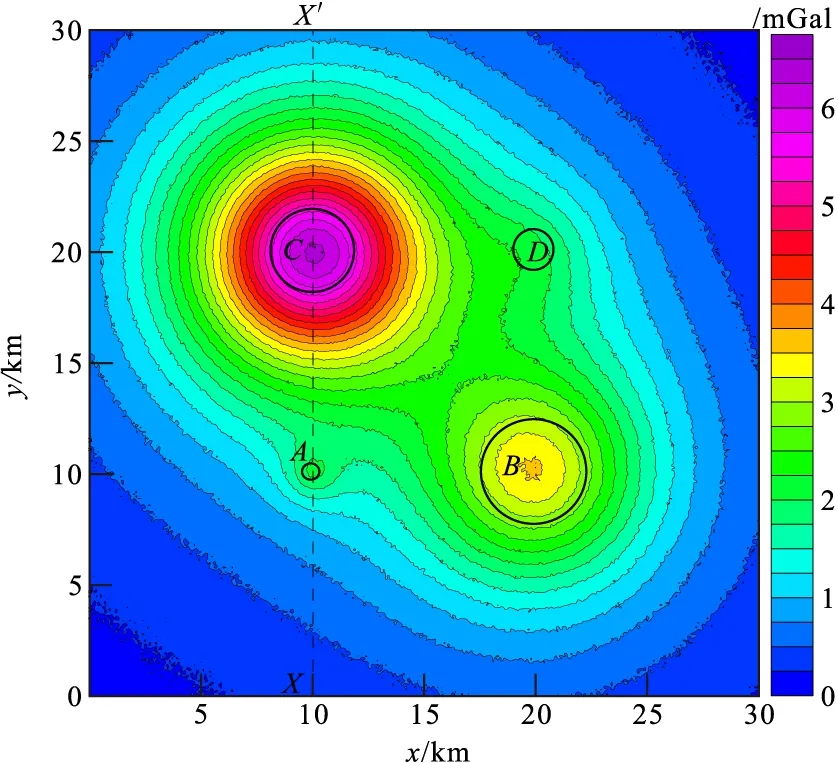
图2 含0.5%噪声的叠加重力异常Fig.2 Combined gravity anomaly including 0.5% random noise

图3是向下延拓10倍时三种迭代法均方误差与迭代次数的关系曲线，可以看出，泰勒级数迭代法迭代误差随着迭代次数的增加而快速递增，最小误差0.42 mGal在n=1时出现；积分迭代法和补偿法迭代误差则是随着迭代次数的增加先减少后增加，存在一个误差极小值，分别为0.10 mGal和0.07 mGal，均显著小于泰勒级数迭代法的。图4是三种迭代法在迭代误差最小时对应的向下延拓10倍的计算结果，可以看出，补偿法无论是在计算稳定性上还是在计算精度上均高于积分迭代法和泰勒级数迭代法，而泰勒级数迭代法的稳定性最差，噪声干扰几乎淹没了地质体A、B、D上方的有效异常。

图3 不同迭代法向下延拓10倍点距误差 与迭代次数关系曲线Fig.3 Relationship curves of iterative errors and iterative numbers using different iterative methods for downward continuation of 1.0 km

图5是积分迭代法、泰勒级数迭代法和补偿向下延拓法选取迭代次数分别为15、1、2 000时的向下延拓20倍点距的计算结果，由于向下延拓深度已超过地质体A的中心埋深，因此理论延拓值无法与实际延拓值进行对比，即无法获得不同迭代方法的误差曲线，此时迭代次数选取是以计算结果图中开始出现不稳定现象为依据。从图5中同样可以看出，补偿法同样具有更高的计算精度和计算稳定性，另外从图5(c)中还可以看出，当延拓深度大于地质体的实际深度时，地质体上方的极大值圈闭外围存在明显的极小负值环状圈闭。为清晰说明这种现象，图6给出了过地质体A、C中心位置剖面的重力及向下延拓重力异常，可以看出向下延拓较好地提高了对地质体A的异常识别能力，向下延拓20倍点距的重力异常在地质体A上方的重力正异常外围出现了边瓣负异常，而边瓣负异常外围则又出现了边瓣正异常(原始异常和向下延拓10倍点距的则无此异常特征)，因此在实际资料处理中可以此异常特征来评价地质体的大致埋深。

3 应用实例

为验证积分迭代法、泰勒级数迭代法和补偿法这三种方法的实用性，选取江西相山铀矿田重力数据进行方法对比试验。相山铀多金属矿田是我国最大的火山岩型铀矿田，位于赣-杭火山岩型铀多金属成矿带与大王山-于山花岗岩型铀多金属成矿带交汇区，其经历了晋宁期、加里东期、海西-印支期造山作用，燕山期时处于NEE向赣杭构造火山岩带西南端与近NS向赣中南花岗岩带的交接地带，发生了强烈的构造-岩浆-成矿活动。相山盆地断裂构造(图7)较为复杂，主构造方向为NE向，而NS向、近EW向、NW向及NEE向断裂同样较为发育。相山盆地中心部位地表岩性比较单一，主要以低密度的碎斑熔岩为主；盆地基底为高密度的青白口纪变质岩，盆地外围四周均有出露；高密度的晚侏罗世砂岩砂砾岩呈现出明显的环形条带状分布。

图4 不同迭代法向下延拓10倍点距的计算结果Fig.4 Results of downward continuation of 1.0 km using different iterative methods(a)理论向下延拓；(b)积分迭代法；(c)泰勒级数迭代法；(d)补偿向下延拓

图5 不同迭代法向下延拓20倍点距的计算结果Fig.5 Results of downward continuation of 2.0 km using different iterative methods(a)积分迭代法；(b)泰勒级数迭代法；(c)补偿向下延拓

图6 过地质体A、C中心位置剖面上的重力及向下延拓重力异常Fig.6 Original gravity and downward continuation gravity anomalies of the profile over the center position of geological body A and C

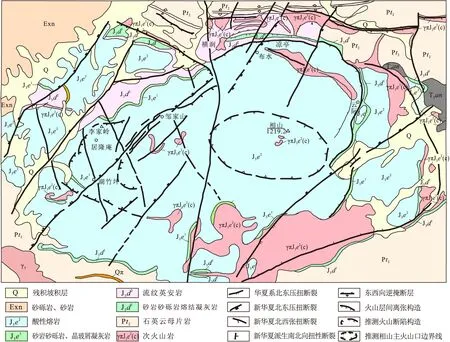
图7 相山矿田地质构造纲要图[18]Fig.7 Geological structure map of Xiangshan orefield

图8(a)是网格点距为250 m的相山布格重力异常，由图8(a)可以看出，布格重力异常整体上呈现为中心重力低、外围重力高，与低密度的碎斑熔岩及高密度的变质岩表现出了良好的对应关系，但重力异常中局部细节特征受区域场影响较大而难以清晰识别。为了提高异常分辨能力，这里采用了积分迭代法、泰勒级数迭代法及补偿向下延拓法分别迭代100次、5次和200次向下延拓5倍点距的计算结果分别见图8(b)～图8(d)，可以看出，积分迭代法和泰勒级数迭代法存在着明显的不稳定现象，仅能识别部分有效异常，而补偿法获得的计算结果显然稳定性较好，并未出现明显的振荡现象，同时，异常分辨率得到了明显提高，局部异常间的特征关系得到了清晰地展示。异常整体上呈现出NE走向，局部异常伴随着NS走向、EW向及NW向，这也恰与该地区的构造特征相一致。另外，向下延拓1.25 km的重力异常在研究区大部分区域均表现为明显的正、负相间出现，表明大多浅部地质体中心埋深则是小于这个延拓深度的。

图8 相山矿田重力数据迭代法向下延拓5倍点距的计算结果Fig.8 Downward continuation 1.25 km height of gravity data in Xiangshan orefield using different iterative methods(a)相山重力异常；(b)积分迭代法；(c)泰勒级数迭代法；(d)补偿向下延拓

4 结论

1)积分迭代法和泰勒级数迭代法仍是高通滤波，在实际资料处理中，需要对原始数据进行滤噪后再使用。补偿向下延拓法为中低通滤波，对高频成分具有较强的压制能力，在实际资料处理中直接使用也可以获得稳定的计算结果。

2)向下延拓可以直接用于估计地质体的大致埋深，可以清晰展示出异常间的相互关系和异常等值线圈闭走向，这些异常特征可为地质体平面赋存状态、边界位置及深度信息等方面提供了借鉴。

3)构造压制高频干扰能力强于广义逆算子的低通滤波器，结合迭代法则在理论上可以获得更为理想的向下延拓结果。

参考文献：

[1] 栾文贵. 位场解析延拓的稳定化算法[J]. 地球物理学报，1983, 26(3): 263-274.

LUAN W G. The stabilized algorithm of the analytic continuation for the potential filed[J]. Chinese Journal of Geophysics, 1983, 26(3): 263-274.(In Chinese)

[2] 梁锦文. 位场向下延拓的正则化方法[J]. 地球物理学报，1989, 32(5): 600-608.

LIANG J W. Downward continuation of regularization methods for potential fields[J].Chinese Journal of Geophysics, 1989, 32(5): 600-608. (In Chinese)

[3] PAWLOWSKI R S.Preferential continuation for potential-field anomaly enhancement[J]. Geophysics,1995,60(2):390-398.

[4] 王延忠，熊光楚. 位场向下延拓组合滤波器的设计和应用[J]. 地球物理学报，1985, 28(5): 537-543.

WANG Y Z, XIONG G C. A combined filter used for the downward continuation of the potential filed[J].Chinese Journal of Geophysics, 1985, 28(5): 537-543. (In Chinese)

[5] FEDI M, FLORIO G. A stable downward continuation by using the ISVD method[J].Geophysical Journal International, 2002, 151(1): 146-156.

[6] 陈生昌，肖鹏飞. 位场向下延拓的波数域广义逆算法[J].地球物理学报，2007, 50(6): 1816-1822.

CHEN S C, XIAO P F. Wavenumber domain generalized inverse algorithm for potential field downward continuation[J].Chinese Journal of Geophysics, 2007, 50(6): 1816-1822. (In Chinese)

[7] 徐世浙. 位场延拓的积分-迭代法[J]. 地球物理学报，2006, 49(4): 1176-1182.

XU S Z. The integral-iteration method for continuation of potential fields[J]. Chinese Journal of Geophysics, 2006, 49(4): 1176-1182. (In Chinese)

[8] 王彦国，张凤旭，王祝文，等.位场向下延拓的泰勒级数迭代法[J]. 石油地球物理勘探，2011, 46(4): 657-662.

WANG Y G, ZHANG F X, WANG Z W, et al. Taylor series iteration for downward continuation of potential field [J]. Oil Geophysical prospecting, 2011, 46(4): 657-662.(In Chinese)

[9] 王彦国，王祝文，张凤旭，等.位场向下延拓的导数迭代法[J].吉林大学学报(地球科学版), 2012, 42(1): 240-245.

WANG Y G, WANG Z W, ZHANG F X, et al. Derivative-iteration method for downward continuation of potential fields[J]. Journal of Jilin University (Earth science Edition), 2012, 42(1): 240-245. (In Chinese)

[10] 张志厚，吴乐园. 位场向下延拓的相关系数法 [J].吉林大学学报(地球科学版), 2012, 42(6): 1912-1919.

ZHANG Z H, WU L Y. Correlation coefficient method for downward continuation of potential field [J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1912-1919. (In Chinese)

[11] 高玉文，骆遥，文武. 补偿向下延拓方法研究及应用 [J]. 地球物理学报，2012, 55(8): 2747-2756.

GAO Y W, LUO Y, WEN W. The compensation method for downward continuation of potential field from horizontal plane and its application [J]. Chinese Journal of Geophysics, 2012, 55(8): 2747-2756. (In Chinese)

[12] 曾小牛，刘代志，李夕海，等.位场向下延拓的改进迭代维纳滤波法 [J]. 地球物理学报，2014, 57(6): 1958-1967.

ZENG X N, LIU D Z, LI X H, et al.An improved iterative Wiener filter for downward continuation of potential fields[J]. Chinese Journal of Geophysics, 2014, 57(6): 1958-1967. (In Chinese)

[13] 刘东甲，洪天求，贾志海，等. 位场向下延拓的波数域迭代法及其收敛性[J]. 地球物理学报，2009, 52(6): 1599-1605.

LIU D J, HONG T Q, JIA Z H, et al. Wave number domain iteration method for downward continuation of potential fields and its convergence [J]. Chinese Journal of Geophysics, 2009, 52(6): 1599-1605. (In Chinese)

[14] 张辉，陈龙伟，任治新，等. 位场向下延拓迭代法收敛性分析及稳健向下延拓方法研究 [J]. 地球物理学报, 2009, 52(4): 1107-1113.

ZHANG H, CHEN L W, REN Z X, et al. Analysis on convergence of iteration method for potential fields downward continuation and research on robust downward continuation method [J]. Chinese Journal of Geophysics, 2009, 52(4): 1107-1113. (In Chinese)

[15] 于波，翟国君，刘雁春，等. 噪声对磁场向下延拓迭代法的计算误差影响分析[J]. 地球物理学报，2009, 52(8): 2182-2188.

YU B, ZHAI G J, LIU Y C, et al. Analysis of noise effect on the calculation error of downward continuation with iteration method [J]. Chinese Journal of Geophysics, 2009, 52(8): 2182-2188. (In Chinese)

[16] 曾小牛，李夕海，牛超，等. 位场向下延拓的波数域正则-积分迭代法[J]. 石油地球物理学报，2013, 48(4): 643-650.

ZENG X N, LI X H, NIU C, et al. Regularization-integral iteration in wavenumber domain for downward continuation of potential fields [J]. Oil Geophysical Prospecting, 2013, 48(4): 643-650. (In Chinese)

[17] 侯重初. 补偿圆滑滤波方法[J]. 石油物探，1981，20(2): 22-29.

HOU Z C. Filtering of smooth compensation [J]. Geophysical prospecting for Petroleum, 1981, 20(2): 22-29. (In Chinese)

[18] 陈越. 相山铀矿田地球物理特征及深部地质结构研究[D]：北京：核工业北京地质研究所, 2014.

CHEN Y. Study on geophysical characteristics and deep geological structures of the Xiangshan uranium orefield. [D].Beijing: thesis of Beijing Research insititute of Uranium Geology，2014. (In Chinese)