基于协同传递机制的形状匹配算法
王江辉 吴小俊
(江南大学物联网工程学院 江苏 无锡 214122)
0 引 言
物体的形状是人类辨别物体的重要参考,对形状的表示和匹配在计算机视觉中一直是个具有挑战性的问题。形状检索算法应用范围较广,在人脸识别、医学影像分析、机器人导航和深度学习等领域中都有形状匹配算法的例子[1-3,16]。近些年,提出了大量基于深度学习的3D形状检索。Zhu等[17]将空间信息复杂的3D形状投影到2D空间,再用自编码器学习2D形状的特征。最后基于这类特征进行3D形状的检索与识别。Hang等[18]用物体的三维数据从不同“视角”所得到的二维渲染图,作为原始的训练数据。用经典、成熟的二维图像卷积网络进行训练,训练出的模型,对三维物体的识别、分类效果比用三维数据直接训练出的模型好。但是2D形状检索依旧是计算机视觉中一个研究热点,尤其是基于轮廓的描述子性能好于其他形状描述子,称为识别特征的首选。
基于轮廓的2D形状检索有2个大致过程: 形状描述和形状相似度计算[4]。形状描述是形状匹配的关键步骤,对形状几何信息描述越到位,形状的检索结果也就越好。但是一个合适的形状特征相似度度量在很大程度上也决定了算法的检索性能。其中,Wang等[4]提出的高度函数(Height function)是以动态规划算法DP(Dynamic programming)测量形状间相似度。而Belongie等[6]提出的经典检索算法——形状上下文SC(Shape Context)则先用卡方检验计算匹配代价矩阵再用匈牙利算法得出最优匹配结果。Shu等[7]提出的轮廓点分布直方图CPDH用地球移动距离EMD(Earth Mover’s Distance)度量直方图之间的相似度。但是CPDH区分剧烈变化的不相似形状时判别能力较弱使得其在大数据集下的检索效果不佳。
Bai等[8]提出了结合两种不同形状描述子的相似度度量的半监督学习框架(Co-transduction)。Co-transduction其实可以看成一种协同传递机制,它有效将半监督学习中的标签传播算法[9]LP(Label propagation)融入形状检索中。核心思想是输入查询形状并赋予一个标签信息,在两种不同形状检索算法下进行迭代检索与标签传播,最后返回与其最相似的目标形状。算法实例如图1所示:(a)由于局部形变,查询形状A与目标形状B、C的SC距离较大。而在(b)中形状A与B的距离更小,因为SC比IDSC对局部形变更加敏感(IDSC用内部距离替换了SC算法的欧式距离)。(c)中形状B与C有相同的姿势也就表明局部形变更少它们的SC距离也相对小。(d)为Co-transduction整合的第二步与第三步,先用IDSC检索出形状B,然后将A与B作为一个整体标签通过SC检索出目标形状C。受上述工作的启发,为了提升CPDH的检索性能,本文有效地整合SC[6]、CPDH[7]的相似度度量形成一个新的Co-transduction。通过对实验结果进行分析,该改进算法能有效地进行形状检索并提升了原始CPDH在大数据集下的检索性能。

图1 示例图
1 特征提取
1.1 轮廓提取
如图2所示,采用标准的Canny算子对目标图像轮廓进行提取,采样点数量依形状复杂度而定。

图2 轮廓提取图
式中:n表示轮廓点的数量,描述图像轮廓。图2中,(a)为初始图像;(b)为用Canny算子提取的轮廓;(c)为采样100个轮廓点的图像;(d)为轮廓图及其最小外接圆的效果图。
1.2 构建CPDH
以点集P为构建外接圆的区域,圆心为目标形状的质心,以等分外接圆的半径和圆周的方式建立图3模型来统计分布在各个网格的轮廓点数。对每一个网格B,得到描述集合Hi={ρi,θi,ni}其中:ρi为第i个同心圆的半径,θi为区域Bi的直径边与x轴正方向所成夹角,ni统计区域Bi中采样点的个数。查询形状的采样点分布信息就可以由B个描述集合所构成的二维直方图H来描述。

图3 极坐标下轮廓点分布
2 基于LP算法的Co-transduction
2.1 构造概率转移矩阵
给定一个形状集X={x1,x2,…,xn}和相似度函数sim:X×X→R+计算每一对形状之间的相似度。假设x1是一幅查询图像,{x2,x3,…,xn}是一组已知的形状数据集。利用sim(x1,xi)计算每一对形状的相似度且递减排序获得一组有序的形状数据集,并且将相似度定义成一个矩阵wij=sim(xi,xj),i,j=1,2,…,n,定义概率转移矩阵P:
(1)
式中:Pi,j表示节点i到节点j的标签传播概率其性质为相似度矩阵wij的行归一化矩阵。基于矩阵P定义一个新的相似度度量S,函数f(xi)=s(x1,xi),i=1,2,…,n。
(2)
函数f(xj)表示目标形状xi与查询形状x1的相似度,由式(1)、式(2)得f(xi)是形状数据集X的加权平均,且正比于权值wij。其中采用迭代方法求解式(2):

(3)
初始化迭代,ft+1(x1)=1,表示赋予查询形状一个标签信息。
2.2 构造相似度转移矩阵
为了将相似度矩阵D=(Dij)转换成一种新的相似度度量,利用高斯核函数构造一个相似度矩阵w:
(4)
式中:σij的大小是基于样本到K-NN平均距离(相似度)的自适应核学习:
σij=α·mean({knnd(xi),knnd(xj)})
(5)
式中:mean({knnd(xi),knnd(xj)})表示样本xi、xj之间的K-NN距离的平均距离;参数α和k是多次实验后获得的最优参数选择。
2.3 LP算法步骤
结合上述矩阵构造,将LP算法应用于形状检索中流程如下:
1) 输入:n×n的行归一化相似度矩阵P,查询形状x1。
2) 初始化f1(x1)=1(已有标签形状);f1(xi)=0,i=2,3,…,n(未标签形状)。
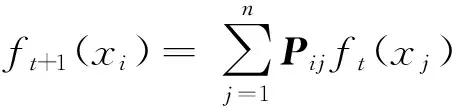
输出:查询形状x1相似度x1:fT。
3 基于Co-Transduction的CPDH检索算法
3.1 算法思想
Co-Transduction利用LP算法[9]获取形状间的上下文信息来提升相似度函数的准确性。输入CPDH度量结果和另一种形状检索算法的度量结果并将它们作为LP算法中的未标签数据集。查询形状作为单独标签数据,在式(2)、式(3)迭代传播标签信息直到所有未标签数据成为标签数据,最后输出与查询形状最相似的目标形状。
3.2 算法实现步骤
在大数据集下计算所有形状间距离相当费时,为了提升算法的时间性能,利用原始相似度度量计算目标形状与查询形状x1前M个最相似的度量结果构造成一个相似度矩阵w。
1) 输入一幅查询图像x1(标签数据),形状数据集X={x2,x3,…,xn}(无标签形状)。
2) 基于一种形状相似度度量S1(例如SC)构造一个M×M概率转移矩阵P1;基于另一种相似度度量S2(例如CPDH)构造一个M×M概率转移矩阵P2。
3) 给定四个集合:Y1,Y2={x1};集合X1=X2=X。
4) 进行m次迭代,迭代过程如下:

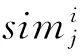
更新集合X1、X2:X1=X1-Y1,X2=X2-Y2,更新后的X1,X2作为下一次迭代的无标签数据集。
5) 整合两种算法得到新定义的相似度函数:
(6)
4 算法时间复杂度分析
根据所述算法流程,进行一次LP算法的迭代时间复杂度为O(n2),n表示数据集中形状的类别数。如上文提及,仅用与查询形状最相似的形状前m个形状构建LP算法的相似度矩阵。因此,LP算法的每次迭代的复杂度是O(M2)。整个LP算法复杂度是O(M2T),T表示迭代次数。易得,Co-transduction的算法复杂度为O(M2Tm),m表示LP的迭代次数。
5 实验结果与分析
为验证改进算法在各个数据集下的有效性,分别选取不同类别的形状数据集进行仿真分析。
实验环境:操作系统Windows 7 64位,CPU i5-6500,12 GB内存,使用软件为MATLAB 2015a。
5.1 Kimia-25与Kimia-99形状数据集
Kimia-25形状数据集[13]共有25个样本6个不同的类别,Kimia-99数据库[14]共有99个样本,每类形状有9个样本,2个数据集剪影如图4所示。

(a) Kimia-25形状数据集 (b) Kimia-99形状数据集图4 两组形状数据集剪影
在本文的验证实验中,设置参数如下:Canny采样点数100个。构建形状描述子时将外接圆圆周12等分,半径5等分,即5ρ×12θ=60个区域块。
表1列出了各种检索算法在Kimia-25数据集下的检索结果,统计并返回前3幅与查询形状属于同一类的形状数目。从表1的结果中可以看出,本文所提改进方法在 Kimia-25数据集下检索结果优于表中其他经典算法。

表1 Kimia-25数据集在不同方法下的检索结果
在Kimia-99数据库进行仿真实验的结果见表2。其中表中数值为与查询形状最相似的前10组目标形状分类正确的具体数目及总和。相比于表2中SC与CPDH,改进算法可以得到更好的匹配结果。通过对两类数据集的仿真,说明在小样本数据集下改进算法能有效进行形状检索并且有较优的识别精度。

表2 Kimia-99数据集下不同方法的检索结果

续表2
5.2 MPEG-7数据集
为验证本文算法在大数据集下的有效性。本次试验在MPEG-7[21]数据集下进行仿真,该数据集共有1 400个形状,共70个类别,每个类别中各有20个有形变的样本。使用Bull-eye[11]方法计算检索精度:将数据集中每个形状都作为查询形状并计算与数据集中所有形状的相似度。将实验结果降序排列取前40个检索结果,再统计这40个形状中与查询形状属于同一个类别的数目。从表3中可以看出,相比于其他算法,本文方法的检索精度较好而且Co-transduction约束条件少,可直接将相似度度量作为算法的输入。

表3 MPEG-7数据在不同方法下的结果比较
6 结 语
本文将半监督学习算法Co-transduction与CPDH有效结合。从实验结果来看,所提算法能取得良好的实验效果,优于原始CPDH算法。但实验中在大数集下的效果还不是特别理想。经分析,其主要原因在于CPDH只考虑到形状的全局特征而对微小形变比较敏感,且Co-Transduction只是一种距离学习框架而不是一种完整的形状描述子。在未来的工作中,将以2D形状检索为基础并结合深度学习研究3D形状检索。
[1] 胡大盟,黄伟国,杨剑宇,等.改进离散曲线演化的形状匹配算法[J].计算机辅助设计与图形学学报,2015,27(10):1865-1873.
[2] Bai X, Rao C,Wang X G,et al. Shape vocabulary: a robust and efficient shape rep-resentation for shape matching[J]. IEEE Transactions on Image Processing,2014,23(9):3935-3949.
[3] 原彧鑫, 周向东. 融合深度及边界信息的图像目标识别[J]. 计算机应用与软件, 2017, 34(4):183-187,220.
[4] 金铭, 汪友生, 边航, 等. 一种基于视觉词袋模型的图像检索方法[J]. 计算机应用与软件, 2017, 34(4):249-254,321.
[5] Ling H, Jacobs D W. Shape classification using the inner-distance[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 29(2):286-299.
[6] Belongie S, Malik J, Puzicha J. Shape Matching and Object Recognition Using Shape Contexts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002,24 (4):509-522.
[7] Shu X, Wu X J. A novel contour descriptorfor 2D shape matching and its application to image retrieval[J].Image and vision Computing, 2011, 29(4):286-294.
[8] Bai X, Wang B, Yao C, et al. Co-Transduction for Shape Retrieval[J]. IEEE Transactions on Image Processing, 2012, 21(5):2747-2757.
[9] Zhu X, Ghahramani Z, Mit T J. Semi-Supervised Learning with Graphs[C]//International Joint Conference on Natural Language Processing,2005:2465-2472.
[10] Latecki L J, Lakamper R, Eckhardt U. Shape Descriptors for Non-Rigid Shapes with a Single Closed Contour[C]//Computer Vision and Pattern Recognition, 2000. Proceedings. IEEE Conference on. IEEE, 2000,1:424-429.
[11] Attalla E, Siy P. Robust shape similarity retrieval based on contour segmentation polygonal multiresolution and elastic matching[J]. Pattern Recognition, 2005, 38(12):2229-2241.
[12] Mokhtarian F, Abbasi S, Kittler J. Efficient and Robust Retrieval by Shape Content through Curvature Scale Space[M]//Image Databases And Multi-Media Search,1996:51-58.
[13] Sharvit D, Chan J, Tek H, et al. Symmetry-Based Indexing of Image Databases[J].Journal of Visual Communication and Image Representation, 1998,9(4):366-380.
[14] Gdalyahu Y, Weinshall D. Flexible Syntactic Matching of Curves and Its Application to Automatic Hierarchical Classification of Silhouettes[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 1999, 21(12):1312-1328.
[15] 郭秀才, 白琳琳, 张学峰. 基于ISM形状模型的目标检测算法[J].计算机应用与软件, 2014,31(4):219-222.
[16] Kim K, Lawrence R L, Kyllonen N, et al. Anatomical 2D/3D shape-matching in virtual reality: A user interface for quantifying joint kinematics with radiographic imaging[C]//3D User Interfaces (3DUI), 2017 IEEE Symposium on. IEEE, 2017:243-244.
[17] Zhu Z, Wang X, Bai S, et al. Deep Learning Representation using Autoencoder for 3D Shape Retrieval[J].Neurocomputing, 2016,204(C):41-50.
[18] Su H, Maji S, Kalogerakis E, et al. Multi-view Convolutional Neural Networks for 3D Shape Recognition[C]//IEEE International Conference on Computer Vision. IEEE, 2016:945-953.

