Quasi Three-Body Decay of D Meson

T.Estabar and H.Mehraban

Physics Department,Semnan University,P.O.Box 35195-363,Semnan,Iran

1 Introduction

It is known that multi-body decays of heavy mesons provide a rich laboratory for studying the intermediate state resonance.Therefore,the multi-body decays are generally dominated by intermediate vector and scalar resonances;this means that there are a resonance state and a pseudoscalar meson which they proceed by quasithree-body decays. For calculating branching ratio of these decays,the products of Br(D −→ RM1M2)and Br(R−→M3M4)are applied.[2]The fact is that the analysis of multi-body D decays using Dalitz plot technique points us to some quasi-three-body D decays.We are interested in Br(D −→ RM1M2)decay extracted from multi-body decay of charmed mesons.Thus,the study

For computing these noted decays,we obtain term of Br(D−→RM1M2)using Feynman diagrams and experimental data is used for term of Br(R−→M3M4).Hence,we present concussions of a search for the multi-body decay including intermediate three-body modes that can decay to these final states.Three-body decay of D meson to Kππ has been analyzed long time ago.[3]In these sorts of three-body decay, final state mesons are supposed to be light.The momentum of output mesons and matrix elements of the amplitude are written by variables s=(pD−p3)2and t=(pD−p1)2,[4−5]and Dalitz plot technique should be used integral from smin,tminto smax,tmaxfor computing of the decay width.This double integral encompasses all angles between the momenta of output mesons.Under factorization approach,the amplitudes of three-body decay can be obtained as separate factorizable parts.We investigated parameters which appear in factored form of hadronic matrix elements.The direct non-resonant three-body decay of mesons generally receives two separate contributions:one from the point like weak transition and the other from the pole diagrams that involve three-point or four-point strong vertices.[6]A study of the new contribution which is indeed related to the decay,has been investigated.It arises from the virtual resonance,which the intermediate meson is the D∗meson resonance or other excited mesons.For the D∗intermediate state depicted in Fig.1,the strong coupling is on the left and weak coupling on the right that the strong coupling constant between D,D∗,and π is large.[7]Besides,there are three chances to form a pair of two particles of particles of the final state.Assume that two particles may make almost stable intermediate state named a resonance R.This is revealed in Dalitz plot as the region of the plot where two-particle invariant is equivalent to the resonant mass.Two-body channels may make more than one resonance.[8]Therefore,in non-resonant de-cays,it can be supposed,according to the reference that a virtual resonance occurred and virtual pole diagrams are considered,while the resonant contribution is an almost stable intermediate state.In the factorization method,thedecay amplitude includes the current-Induced process with a meson emission and annihilation process.In the case of⟨D0→ π+π−⟩× ⟨0 →both π mesons are expressed in the form factor andmeson is expressed in the decay constant.In the case ofthe matrix elements of vector and axial vector currents between D0andmeson states by applying D∗+pole.We also investigated the matrix elements of D0−→ K−π+ω decay which consists of⟨D0→ K−ω⟩×⟨0→ π+⟩where the matrix elements D0to Kω mesons are computed by applying D∗0pole,⟨D0→ K−⟩×⟨0→ π+ω⟩where the matrix elements D0to K transition multiplying πω arising from the vacuum,the emission process⟨D0→ ω⟩× ⟨0→ K−π+⟩where K and π mesons are placed from the vacuum,and⟨D0→ 0⟩×⟨0→ K−πω⟩the emission annihilation matrix element.Moreover,the D0−→ K−π+ϕ decay includes⟨D0→ K−ϕ⟩×⟨0 → π+⟩,⟨D0→ K−⟩×⟨0 → π+ϕ⟩,and⟨D0→ 0⟩× ⟨0 → K−π+ϕ⟩.The matrix elements D0to K−ϕ can be computed by applyingpole.

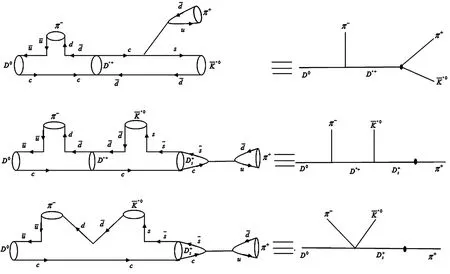
Fig.1Point like and pole diagrams for D−→¯K∗(892)0π+π−decay.

2 The Analysis of Amplitude

It is obvious that under the narrow width approximation,we can calculate the branching ratio of decays.Thus the multi-body decay rate obeys the factorization relation[9]

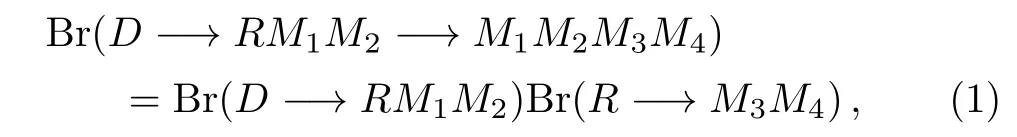
with R being a scalar or a vector meson resonance and M1,M2,M3,and M4are vector and pseudoscalar final states mesons.We have to calculate the branching ratios of the D −→ RM1M2by using the factorization approach and using the experimental results for the Br(R −→ M3M4)decays shown as[1,10]

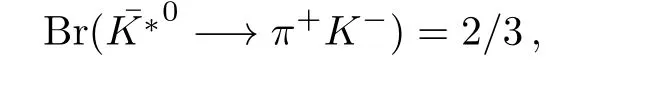
In this section,the amplitude and branching ratio ofand K−π+ϕ are obtained by using the factorization method.We have to contemplate the non-resonant and resonant contributions separately.Hadronic weak decays are evaluated by the effective weak Hamiltonian,[11]

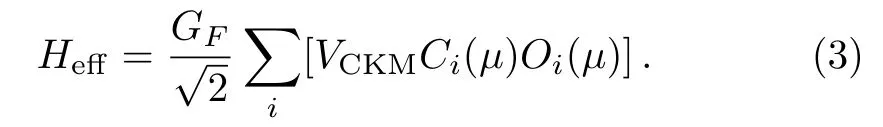
In the above equation,the GFdefines the Fermi coupling constant,the coefficients VCKMare explained elements of Cabibbo-Kobayashi-Maskawa(CKM)and Ci(µ)are the Wilson coefficients,which are evaluated at the typical en-ergy release in two-body non-leptonic D meson decays.[12]

2.1 D0−→∗(892)0π+π−(∗(892)0−→π+K−)

Feynmandiagramsforthethree-bodyD0−→decay can be plotted.The amplitude of this decay includesThus,under the factorization hypothesis,the decay amplitudeis given by

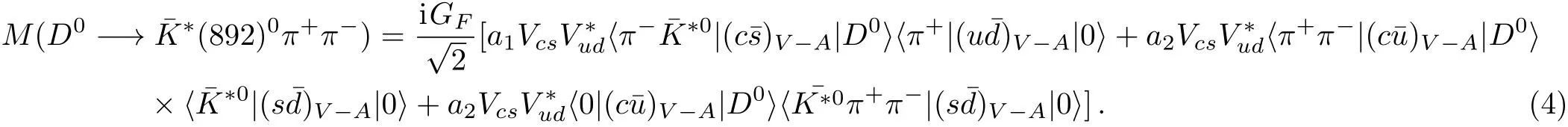
We should consider non-resonant and resonant contributions distinctly.

(i)Non-resonant contribution:The three-body matrix elements for the current-induced process×|D0⟩have the following general form as[13]

We need to consider point-like and pole diagrams that involve three-point or four-point strong vertices.We also require the strong coupling constant of D∗Dπ and DDsππ.The form factors w±and r for the non-resonant decay are evaluated from these diagrams as[14]

where g is a heavy-flavor independent strong coupling.The vector meson’s decay constant is defined[15]

Therefore,we are led to

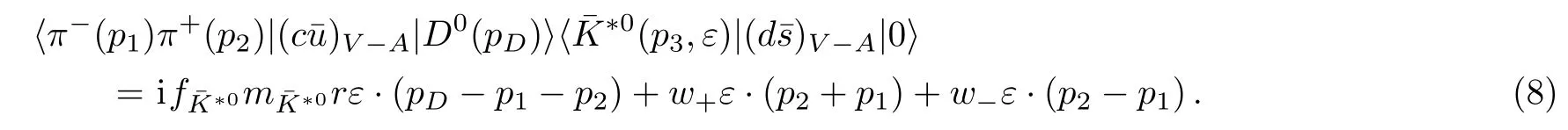
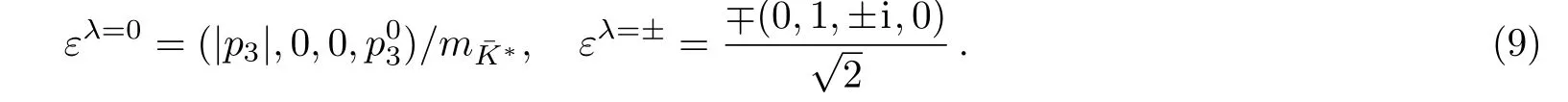
Under the Lorentz condition,ε·(pD−p1−p2)=ε·p¯K∗=0.We also obtain multiplying of the 4-momentum as

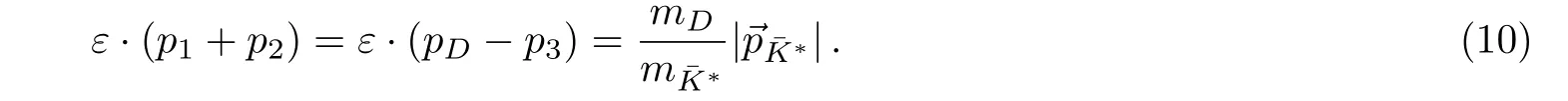
We investigate another matrix elementAccording to Fig.1,the D∗+pole contribution fordecay has been considered by[16]

The strong vertex is expressed as[17]

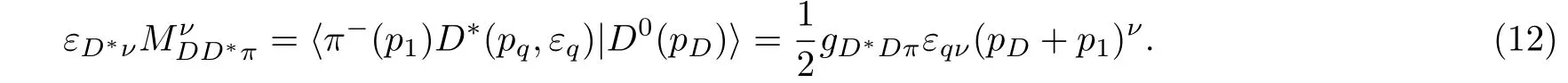
Under the factorization approximation,the weak vertex can be written

The pseudoscalar meson’s decay constant is defined as[18]

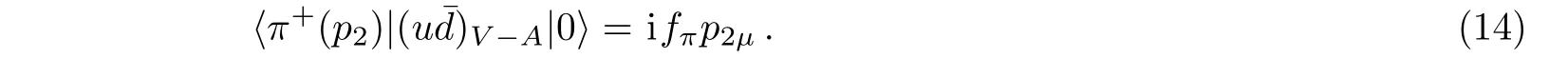
The hadronic matrix elements for D∗−→K∗can be described as the following[19]

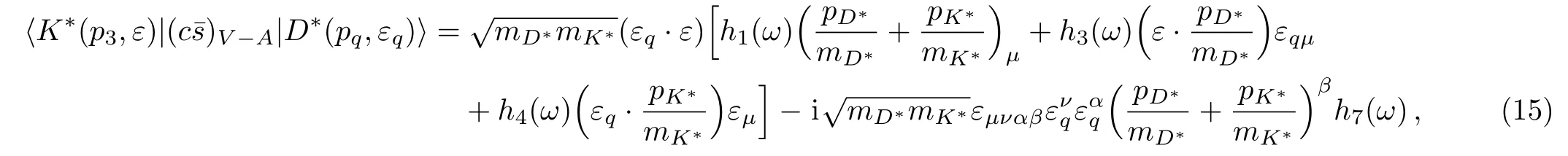
here,ω =pq·p3/mqm3.Form factors in the lowest order under heavy quark expansion become

ε(ω)is the universal Isgur-Wise function which could be written as

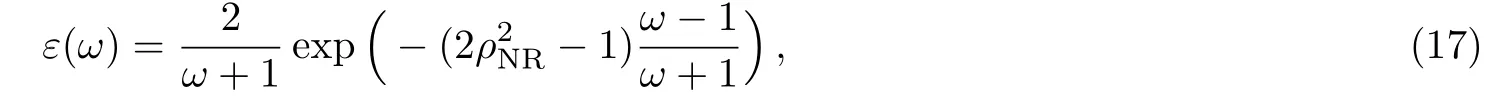
one can obtain close to ω=1

Now the pole contribution can be obtained

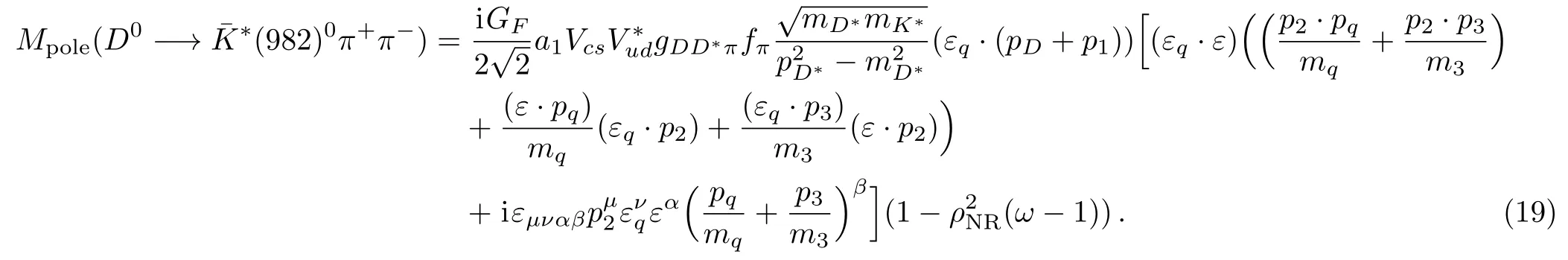
Consider the decay of the D meson into three particles of mass M1,M2,M3and mark their 4 momenta by pD,p1,p2,and p3.Then the energy-momentum conservation could be shown by:

Define the three following invariants that are not independent as:

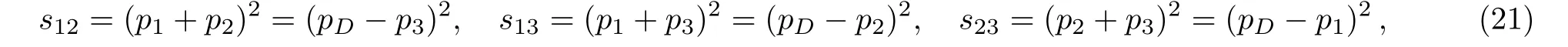
according to the definition of 4 momentum conservation,we have from invariants

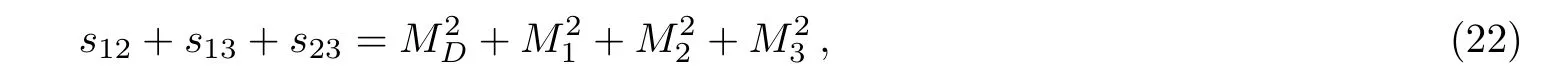
we let s12=s and s23=t.The framework in rest state of the D meson is considered,when D meson decays to final state mesons.Then,the momentum vector element of the D meson is zero

Assumed the movement of one of the final state mesons is along the z-axis,then the momentum of the D meson and the final mesons are presented by

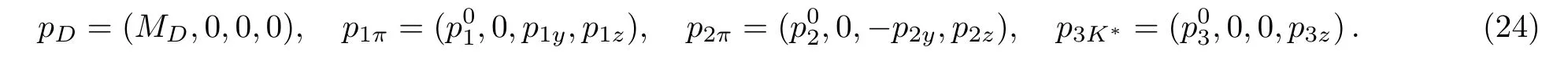
Eventually the decay amplitude of pole contribution can be expressed as

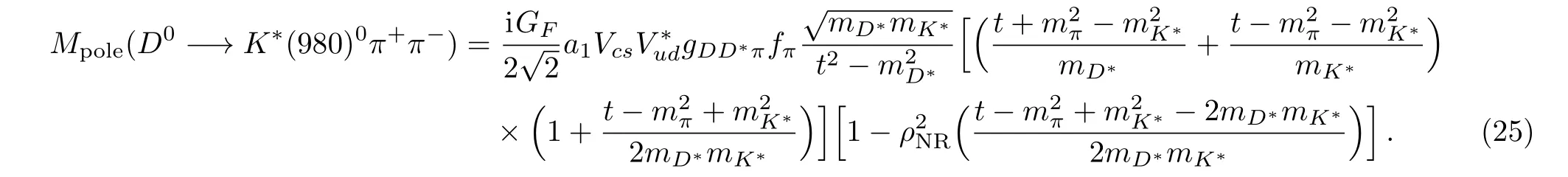
The matrix elements of annihilation process are written by[20]

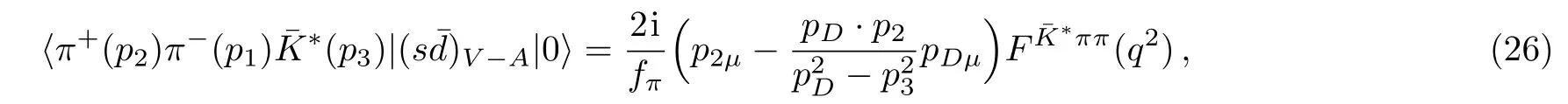
form factor F(q2)in the above equation is described as

Λχ=830 MeV is the chiral-symmetry breaking scale.

(ii)Resonant contribution:The three-body matrix element ⟨P1P2|Vµ|D⟩can receive a contribution from Vector mesons and scalar resonances.Resonant effects are explained in terms of BreitWigner formalism

The channels of three-body matrix element⟨π−(P1)π+(P2)|V −A|D0(pD)⟩can receive terms through intermediateresonance such as Vi=ω,ρi,...,Si=f0(980),f0(1370),...The other three-body matrix elementA|D0⟩receive K1(1270),K1(1400),K∗(1410)and K∗(1680).We need the form factors for D → V and D −→ A transition,which is defined as the following as[21−22]

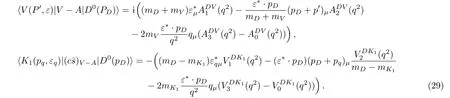
The physical states of axial vector mesons K1(1270)and K1(1400)are mixtures of two separate sorts of K1Aand K1Bwhere they are the singlet1P1and the triplet3P1states,respectively.[23]

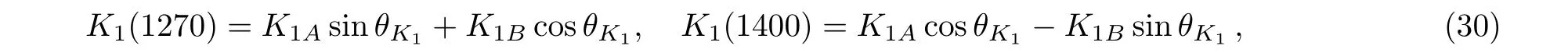
where θK1is the mixing angle.As noticed before,the form factor for D → A transition is stated in Eq.(29).We are led to

Also notice that gVi→P1P2and gSi→P1P2are the coupling constants for vector and scalar mesons.We use the partial

width for their value[13]

The form factor Aiapplied in Eq.(31)can be written by the following parameterization[24]

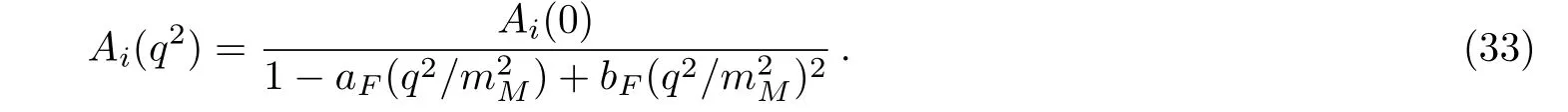
The decay width of three-body is written by[16]

where,

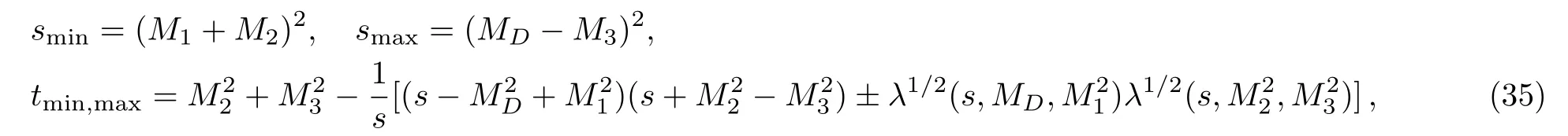
where,λ(x,y,z)=x2+y2+z2−2(xy+xz+yz).

2.2 D0−→ K−π+ω(ω −→ π+π−π0)

The D0−→ K−π+ω decay amplitude contains ⟨D0−→ K−⟩⟨0 −→ π+ω⟩,⟨D0−→ K−ω⟩⟨0 −→ π+⟩,⟨D0−→ω⟩⟨0 −→ π+K−⟩and ⟨D0−→ 0⟩⟨0 −→ K−π+ω⟩factorizable terms,based on the factorization method.Therefore,the factorizable amplitude for this decay has the expression

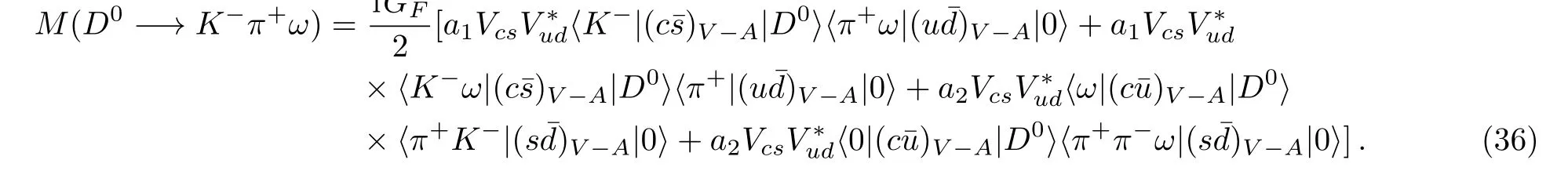
(i)Non-resonant contribution:The form factor for D−→P transition is described by[24]

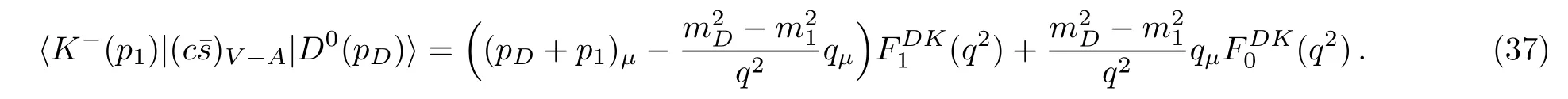
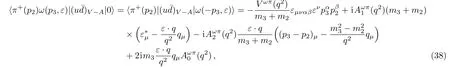
where q=p2+p3.Then,all of the form factors could be written in terms of the Isgur-Wise function ε(ω)for exampleUsing Eqs.(37)and(38),we obtain multiplying two-body matrix elements

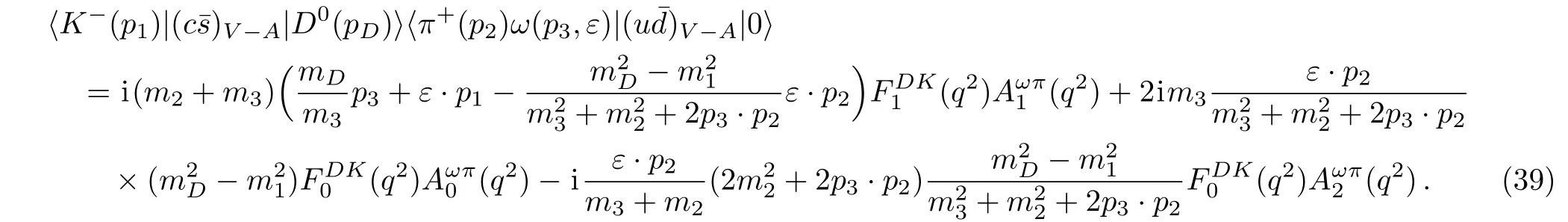
The three-body matrix elementcan be computed by applying D∗+pole,the strong vertex is expressed as

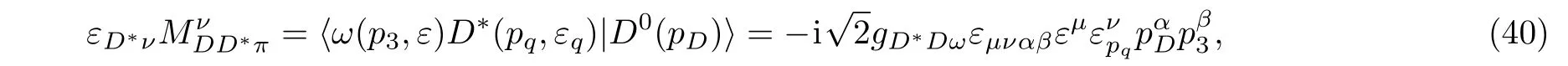
here pq=p−p3.The weak transition is determined as the following

The matrix elements for D∗−→ K and D −→K can be determined as[16]

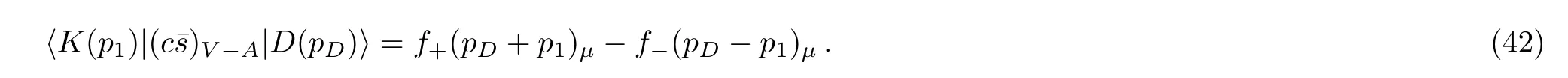
The form factors Tis and f±are defined as follows

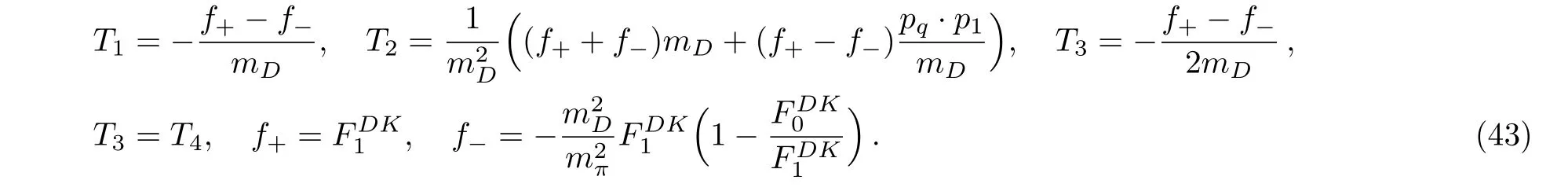
Substituting relations 40,41,and 42 in Eq.(11),the amplitude relating to pole contribution for D0−→Kπω can be expressed by

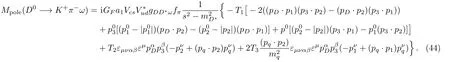
In order to compute the other term in Eq.(36),the two-body matrix elementsare considered by

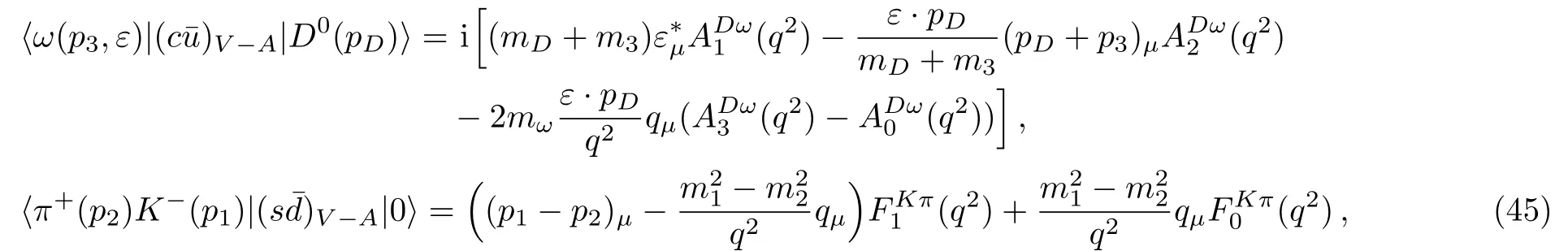
using Γ∗=200 MeV.We are led to

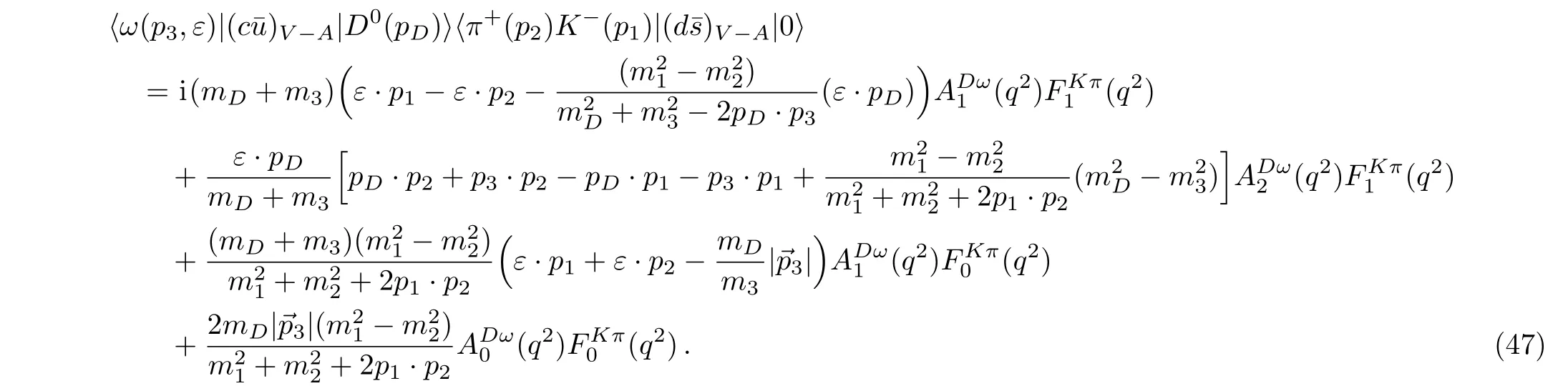
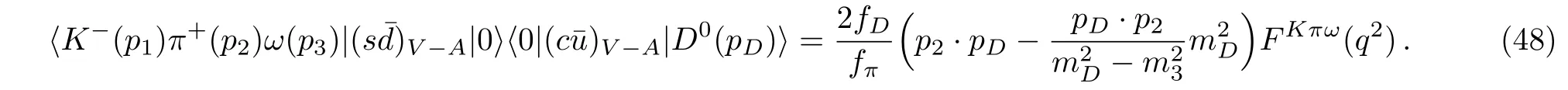
(ii)Resonant contribution:To proceed,we should investigate the resonance contribution of decay D0−→K−π+ω decay.The two body matrix element⟨K−π+|(¯sd)V−A|0⟩receive contribution from scalar and vector resonances.

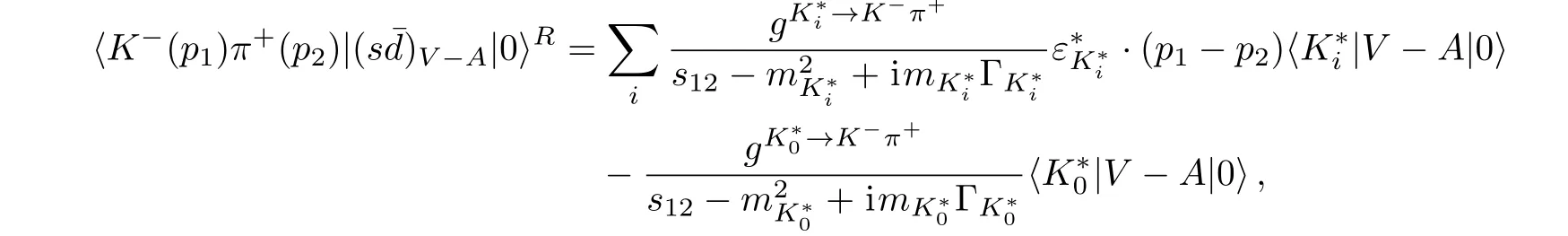
The emission-annihilation matrix element is assumed according to Eq.(26).Therefore,we obtain

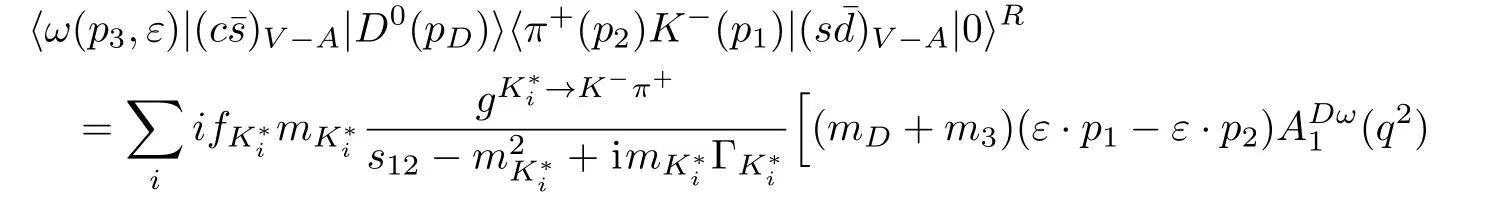
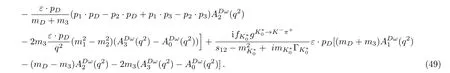
Note that the three-body matrix element⟩can also receive contribution from K1(1400)resonance.

We are led to

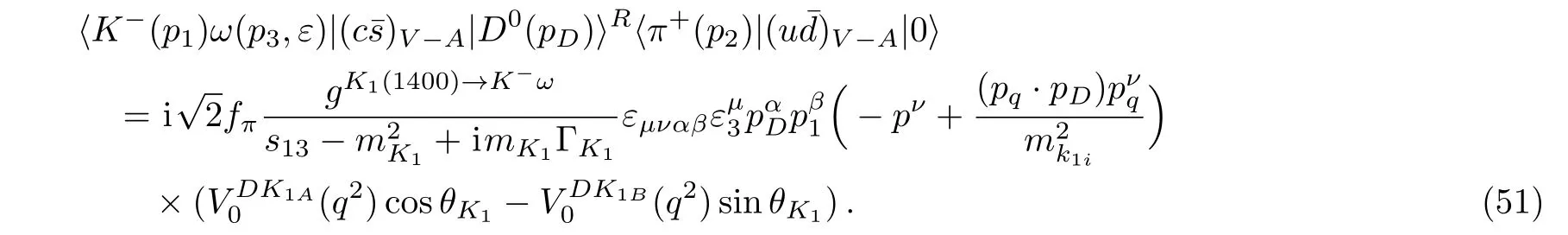
2.3 D0−→ K−π+ϕ (ϕ(1020)−→ K+K−)

The D0−→ K−π+ϕ decay amplitude includes⟨D0−→ K−ϕ⟩⟨0 −→ π+⟩,⟨D0−→ K−⟩⟨0 −→ π+ϕ⟩,and ⟨D0−→0⟩⟨0−→ K−π+ϕ⟩terms.Thus,the factorizable amplitude for this decay is written by

(i)Non-resonant contribution:Three-body matrix elementcan be computed by applying thepole contribution.As for this pole contribution,we shall describe the strong and weak vertices.The general expression for the strong vertex is described as

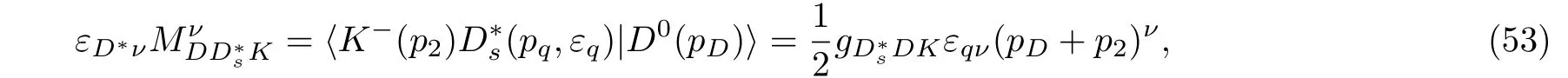
and the weak vertex is defined as

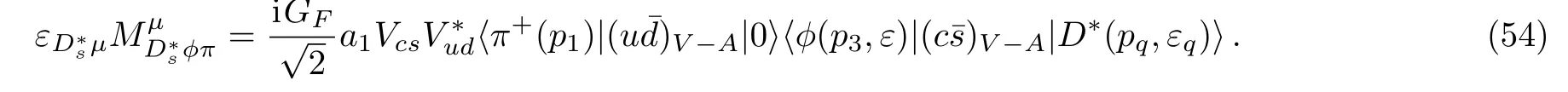
The hadronic matrix element for−→ ϕ has the similar expression as Eq.(15).Therefore,the decay amplitude of pole contribution can be expressed

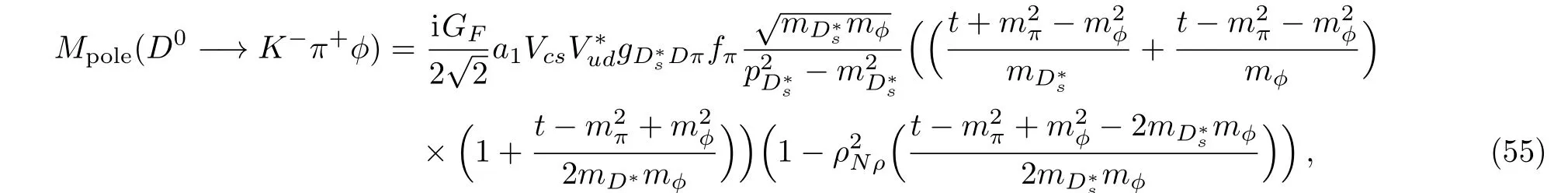
here pD∗s=p1+p3.Note that the matrix elementscan be computed by applying Eqs.(37)and(38).Therefore,We are led to

Eventually,the matrix elements of annihilation process have the similar expression as Eq.(48).Now,the amplitude of each decay obtained is replaced in the relation of the decay width.

3 Numerical Result

We require to determine the input of several physical ingredients for numerical analysis.The Fermi coupling constant,GF,is taken to be equal to 1.66× 10−5GeV.

The value of the decay constants and meson masses in units of MeV are[1,25]

Table 1 The value of Wilson coefficients ciat two renormalization scaleµ.

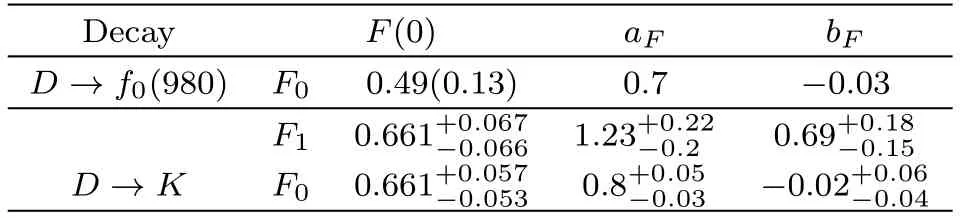
Table 2 The parameters for D→f0(980)and D→K transition.

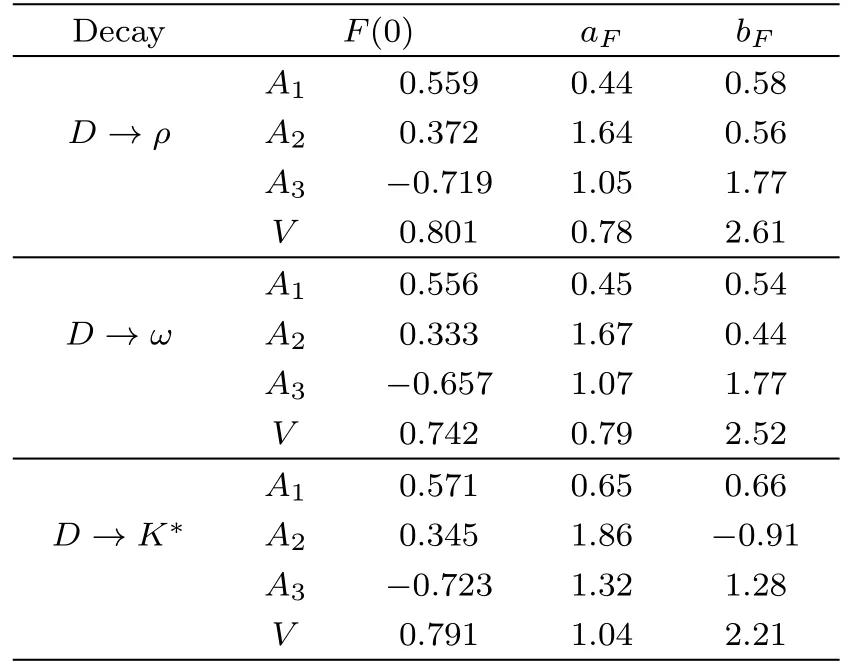
Table 3 The form factors for D → ρ,D → ω,and D→K∗transition.

The value of Ciat the scaleµ=Mcandµ=1 GeV are given in Table 1.[9−10]Parameters in the form factor of FDK(q2)used in Eq.(39)and D−→f0transition calculated by fitting to the covariant light-front model are depicted in Table 2.The value in parentheses are the form factor computed using the ISGW2 model.[24,28]The form factorsandare given in Table 3.[29]Using the relevant parameters to these decays,branching ratios of these decays at two scales MCand 1 GeV are calculated as shown in Table 4.It is necessary to say that the theoretical uncertainties in the computations depicted in Table 4 correspond to the masses,decay constant and form factors e.g.FDK.In addition,the theoretical uncertainties come from the CKM matrix element and coupling constant,e.g.gD∗Dπ=17.9± 0.3± 1.9.According to the investigations,the coupling constant has the greatest effect on the value of uncertainties.The measured values in these two scales are not much different.

4 Conclusion

In this research,we have computed the branching ratios of(ϕ(1020) −→ K+K−)decays obtained from studies of four-body decays.For this purpose,the branching ratios of hadronic three-body decays are evaluated by using the factorization method.Then,obtained branching ratios multiplied by experimental information channels.

In order to examine the branching ratio of threebodyand D0−→ K−π+ϕ decay,we investigated resonant and non-resonant amplitudes.There are some tree diagrams for these decay modes,so that,vector and pseudoscalar mesons are placed in the form factor where Matrix elements can be evaluated by using B∗pole.Besides,these decays receive intermediate mesons such as decay modewhich are intermediate states fordecay and intermediate statesdecay.The need to say that both theand K−π+ω decays include resonant and non-resonant contributions,while D0−→ K−π+ϕ decay only includes non-resonant contribution.In addition to these decays are dominated by non-resonant background and approximately near the experimental results.In fact the calculated resonances are small compared to experimental results.In summary,calculated branching ratios for the sum of non-resonant and resonant amplitudes indicated on the Table 4 are consistent with experimental values from PDG arranged.The value on Table 4,indicates,that branching ratios at the renormalization scaleµ=MCcompared with calculated branching ratios at the renormalization scaleµ=1 GeV have a little difference.

Table 4 The branching ratio of decays at two scalesµ=MCandµ=1 GeV.

[1]K.A.Olive,et al..(Particle Data Group),Chin.Phys.C 38(2014)and 2015 update.

[2]H.Mehraban and B.Mohammadi,Adv.High Energy Phys.2013(2013)989843.

[3]R.H.Dalitz,Phil.Mag.44(1953)1068.

[4]B.Bajc,S.Fajfer,R.J.Oakes,et al.,Phys.Lett.B 447(1999)313.

[5]S.Fajfer,R.J.Oakes,and T.N.Pham,Phys.Rev.B 60(1999)054029.

[6]H.Y.Cheng,C.K.Chua,and A.Soni,Phys.Rev.D 76(2007)094006.

[7]A.Deandrea,R.Gatto,M.Ladisaa,et al.,Phys.Rev.D 62(2000)036001.

[8]A.Wuethrich,arXiv:hep-ph/0507058.

[9]H.Y.Cheng,Int.J.Mod.Phys.A 23(2008)3229.

[10]H.Y.Cheng,C.K.Chua,and K.C.Yang,Phys.Rev.D 73(2005)014017.

[11]H.Y.Cheng,C.K.Cheung,G.L.Lin,et al.,J.High.Energy.Phys.028(2016).

[12]H.N.Li,C.D.Lu,and F.S.Yu,Phys.Rev.D 86(2012)036012.

[13]H.Y.Cheng and C.K.Chua,Phys.Rev.D 88(2013)114014.

[14]H.Y.Cheng and C.K.Chua,Phys.Rev.D 89(2014)074025.

[15]W.Lucha,D.Melikhov,and S.Simula,Phys.Lett.B 735(2014)12.

[16]H.Y.Cheng and K.C.Yang,Phys.Rev.D 66(2002)054015.

[17]B.Mohammadi and H.Mehraban,Adv.High Energy Phys.2012(2012)203692.

[18]W.P.Chen,Y.C.Chen,T.W.Chiu,et al.,Phys.Lett.B 736(2014)231.

[19]B.Mohammadi and H.Mehraban,Can.J.Phys.93(2015)339.

[20]B.Mohammadi and H.Mehraban,Adv.High Energy Phys.2014(2014)451613.

[21]M.A.Paracha,B.El-Bennich,M.J.Aslam,and I.Ahmed,J.Phys.Conf.Ser.630(2015)012050.

[22]M.Sayahi and H.Mehraban,Adv.High Energy Phys.2012(2012)494031.

[23]H.Y.Cheng,Phys.Lett.B 707(2012)116.

[24]J.M.Flynn,T.Izubuchi,T.Kawanai,et al.,Phys.Rev.D 91(2015)074510.

[25]V.Bashiry,Adv.High Energy Phys.2014(2014)503049.

[26]W.Roberts,arXiv:hep-ph/0204260(2002).

[27]X.J.Chen,H.F.Fu,C.S.Kim,and G.L.Wang,J.Phys.G:Nucl.Part.Phys.39(2012)045002.

[28]Y.L.Wu,M.Zhong,and Y.B.Zuo,Int.J.Mod.Phys.A 21(2006)6125.

[29]B.El-Bennich,O.Leitner,J.P.Dedonder,and B.Loiseau,Phys.Rev.D 79(2009)076004.