高架城市轨道交通车辆及桥梁振动的理论研究
杭 锦 张允士
(1.南京地铁运营有限责任公司,210012,南京;2.北京交通大学土木建筑工程学院,100044,北京∥第一作者,工程师)
伴随着城市轨道交通的快速发展,轨道交通影响下的环境振动也越来越受到人们的关注[1-3]。振动在国际上已被列为七大环境公害之一,而交通系统引起的振动,由于其影响人群数量大、持续时间长、振动强等特点,己经引起了公众的强烈反应。因此,研究高架城市轨道交通引起的车辆及桥梁的实际振动情况就显得十分必要。近年来,科研人员在对地铁产生的环境振动、波的传播规律以及对于振动控制方面做了大量的研究并取得了显著的成果[4-10]。南京地铁1号线南延线某高架区间自运营开通以来存在列车通过时产生不明原因的上下振动现象,不仅影响乘客的舒适度,而且可能危及高架桥梁的寿命安全。通过理论分析能够较为全面地了解地铁列车过桥时的列车及桥梁状态。本文主要从如下三方面进行理论分析:列车过桥时的车桥共振条件,车桥耦合振动的仿真模拟计算,不同影响因素对于车桥振动的影响。
1 地铁高架区段车桥共振条件
研究的高架线路区间采用整体道床,高架桥总长度为2 579 m。高架桥梁体为单箱单室斜腹板简支箱梁,基本跨径为30 m,采用等高度梁。
线路最小曲线半径800 m,曲线地段不设轨距加宽;线路最大坡度为18‰,轨道结构高度(内轨顶面至梁面的高度)为500 mm。该区间使用两种类型扣件,分别与相应的轨枕配套使用:DTVII2型高架无砟小阻力弹条扣件及短轨枕,用于一般减振地段;Ⅲ型轨道减振器扣件及短轨枕,用于较高减振要求的地段。
对于车桥系统,运行的列车是移动荷载,当列车车速、载重发生变化时,加载频率也会随之改变。当列车车速达到某个特定值时,车桥体系中的车桥频率可能接近或者相同,此时就会产生共振现象。列车所受的外荷载为列车通过桥跨结构的周期性线路不平顺,所研究区段高架桥均为L=30 m的等跨简支梁。假设列车以速度v通过桥面,则相当于桥梁对列车车辆施加了一个频率fv=v/L的周期性荷载。考虑列车速度范围为50~80 km/h,经计算得到其外荷载输入频率见表1。
1列地铁列车由6节车厢组成,依次记为A车、B车、C车、C车、B车、A车。车辆最大轴重16 t,最高运行速度80 km/h。A车、B车、C车在不同满载率条件下的自振频率见表2。车型与满载率共计15个组合的振动相同,分别为第1阶车体沉浮、第2阶车体点头、第3阶车体沉浮、第4阶车体点头、第5阶前转向架点头、第6阶后转向架点头。

表1 不同车速下桥梁周期性不平顺引起的外荷载输入频率
区间内地铁列车最高运行速度为70 km/h,此车速下外荷载输入频率为0.648 Hz,将其与车辆自振频率进行对比,在所有车型、满载率条件下,车辆自振频率均高于桥梁周期性不平顺引起的外荷载输入频率。图1给出了车辆一阶自振频率与外荷载输入频率的对比,因此可排除车桥发生共振的可能性。
2 车桥耦合振动分析
2.1 动力学分析理论基础
列车通过桥梁引起的振动即为列车-轨道-桥梁耦合振动、列车车辆通过城市高架桥梁时,对桥梁结构会产生动力冲击,使桥梁结构发生振动,而同时桥梁的振动也会对桥上运行的列车产生动力作用,对列车运行的安全性及舒适性会造成一定影响。列车、轨道、桥梁分别通过轮轨及桥轨的相互作用关系耦合成一个整体大系统,在系统激励的作用下,产生耦合振动,从而引发各部件的振动响应。轮轨动态相互作用在这一耦合系统中,作为连接列车与桥梁结构的纽带,起到了核心作用[11-14]。

表2 调整参数后的车辆自振频率

图1 车辆一阶自振频率与外荷载输入频率的对比
列车-轨道-桥梁系统动力学方程可以表述为车辆系统方程、轨道系统方程以及桥梁系统方程,且这3个方程具有统一的形式:
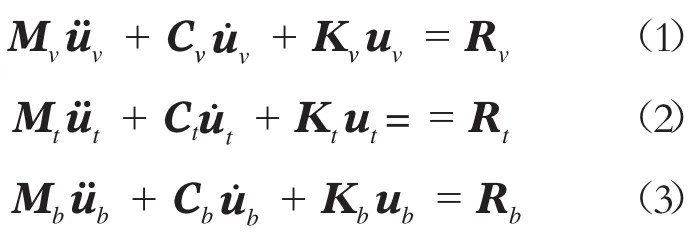
上述式中:Mv,Mt,Mb分别是列车、轨道、桥梁系统的质量矩阵;Cv、Ct、Cb分别是列车、轨道、桥梁系统的阻尼矩阵;Kv、Kt、Kb分别是列车、轨道、桥梁系统的刚度矩阵;uv、ut、ub分别是列车、轨道、桥梁系统的广义位移向量;u˙v、u˙t、u˙b、分别是列车、轨道、桥梁系统的广义速度向量;üv、üt、üb分别是列车、轨道、桥梁系统的广义加速度向量;Rv、Rt、Rb分别是列车、轨道、桥梁系统的广义荷载向量。
式(1)为列车系统方程,式(2)为轨道系统方程,两者通过轮轨关系相耦联,式(3)为桥梁系统方程,式(2)与式(3)通过桥轨关系相耦联。这几个方程一起构成了车线桥系统方程组。
通常采用全过程迭代法对此类方程组进行求解。在此方法中,首先将桥梁子系统视为刚性,对车辆结构的独立方程进行求解,以此得到车辆运动及轮轨作用力时程;其次将轮轨作用力施加给桥梁结构,对桥梁结构的独立方程进行求解,得到桥梁结构的运动状态;最后将求解得到的桥面运动时程与轨道不平顺进行叠加,叠加后作为再一次的车辆系统激励进行下一步迭代。图2给出了全过程迭代法的流程图,该方法一般采用轮轨间相互作用力作为收敛判断的对象。

图2 全过程迭代法流程图
2.2 仿真计算
由于所研究高架轨道区间地处郊区,乘客较少,试验期间平均客座比仅为44%,因此本计算只考虑满载率为0%、25%、50%的情况。计算车速为50~80 km/h,每5 km/h为一个速度等级。
钢轨采用60 kg/m,线路最小曲线半径为800 m。结合线路实际状态,计算中考虑DTVII2扣件和Ⅲ型减振器扣件两种线路刚度。DTVII2扣件和Ⅲ型减振器扣件间距均为620 mm,DTVII2扣件刚度取为每个30 kN/mm,Ⅲ型减振器刚度取为每个12 kN/mm。桥跨30 m,梁高1.8 m,桥梁按等截面考虑,不考虑桥墩及基础。桥梁截面形式见图3。选取20孔跨度30 m的简支梁建立桥梁模型。目前,对地铁列车轨道不平顺的研究较少,参照类似工程,本计算采用德国低干扰谱转换的时域样本作为系统激励。不平顺样本序列全长4 000 m,不平顺测点间距0.5 m,其高低不平顺幅值为11.80 mm,水平不平顺幅值为10.79 mm。
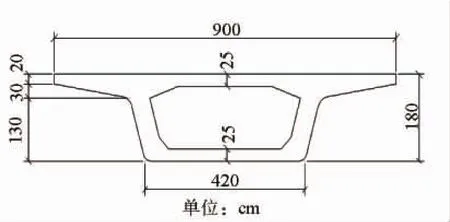
图3 桥梁横截面
列车分别在满载率0%,25%,50%的条件下,以50、55、60、65、70、75、80 km/h 的速度,在采用 DTVII2型扣件的轨道上运行通过桥梁时,车桥动力响应指标分析结果见图4—图9。
由计算结果可见,行车速度50~80 km/h范围内,采用两种扣件情况下,列车轮重减载率均小于GB 5599—85《铁道车辆动力学性能试验鉴定规范》第3.3.3.1条中规定的第二安全限度0.6的标准,列车Sperling指标均小于上述规范第2.3.2条中规定的平稳性等级1级标准2.50;借鉴《高速铁路设计规范(试行)》第7.6.3条规定,列车车体竖向加速度均小于竖向加速度半峰值1.3 m/s2的标准。

图4 不同满载率下动力系数的变化
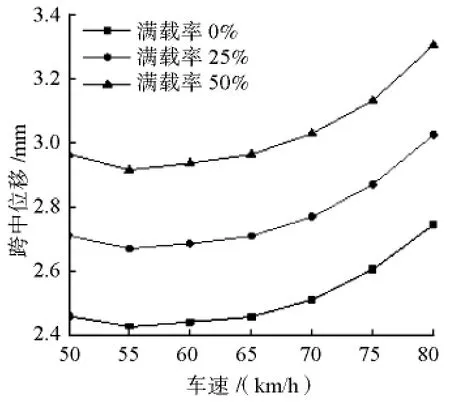
图5 不同满载率下跨中位移的变化

图6 不同满载率下跨中加速度的变化

图7 不同满载率下轮重减载率的变化

图8 不同满载率下车体加速度的变化

图9 不同满载率下列车Sperling指标的变化
3 不同影响因素对车桥振动的影响
3.1 列车车速及满载率对车桥振动的影响
为了探究列车车速及满载率对车桥振动的影响,以线路使用DTVII2扣件为例,分析不同车速、不同满载率条件下,列车及桥梁动力响应参数的对比变化。
(1)由图4—图6可见,车速及车辆满载率对桥梁动力系数影响不大;车速及车辆满载率的变化对桥梁跨中位移影响显著,随着车速的增加和车辆满载率的提高,桥梁跨中位移随之增大;车辆满载率越高,桥梁跨中加速度越大,在50~55 km/h、70~80 km/h车速范围内,车速提高,跨中加速度增大。
(2)车速及满载率对车辆振动的影响。由图7—图9可知,车速及车辆满载率对车辆轮重减载率影响不大;随着车速的提升,车体加速度与车辆舒适性指标也随之增加,在60~70 km/h车速范围内,满载率的增加会使车体加速度及舒适性指标有一定程度的降低。
3.2 减振扣件对车桥振动的影响
为了分析减振扣件对车辆和桥梁振动的影响,以满载率50%为例,分析桥梁、车辆响应在线路使用DTVII2扣件与Ⅲ型减振器时的对比及变化,见图10~图13。
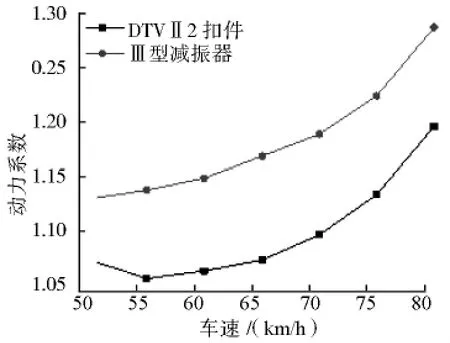
图10 不同扣件时桥梁动力系数的对比

图11 不同扣件时桥梁跨中位移的对比

图12 不同扣件时列车轮重减载率的对比
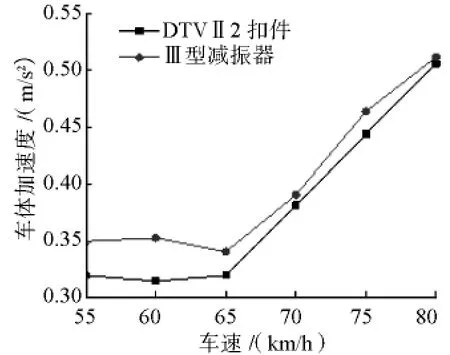
图13 不同扣件时车体加速度的对比
由图10—图13可知,DTVII2扣件相比于Ⅲ型减振器,可使桥梁动力系数及跨中位移有所减小,列车轮重减载率有所增加,车体加速度有一定程度减小。
综上可知,随着车速的提高,桥梁动力响应及车辆动力响应均有不同程度的增大,车桥振动系统受列车运行速度的影响较大;车辆满载率提高,乘客人数增加均会导致列车车体参振质量变大,桥梁的跨中位移及跨中加速度随之增大,而列车车辆的振动状态会有所改善,车辆的竖向振动有一定程度的减小;在满足环境振动标准的前提下,采用例如DTVII2扣件这类刚度较大的扣件,可降低车-桥系统振动,提高地铁列车的乘坐舒适性。
4 振动控制措施
地铁运营管理部门须密切关注所研究区段的振动状态,根据列车振动情况的发展状况酌情实施如下减振措施:
(1)当车体振动过大时,控制车速是可供减振的方法之一。
(2)加强对地铁高架线路的日常监测与维护。如加强对线路钢轨进行打磨和涂油等维修管理。
(3)在满足环境振动标准前提下,采用如DTVII2扣件这类刚度较大的扣件,可降低车-桥系统振动,尤其是车体的振动,以提高地铁列车的乘坐舒适性。
5 结语
地铁列车引发的环境、高架桥梁、线路结构以及列车本身的振动是一个系统性问题,其根本原因在于车-线-桥动力耦合系统中各子系统在外界激励下产生的共振。对于高架城市轨道交通,车速、车辆满载率及轨道线路的减振扣件对列车过桥时的车桥振动均有影响,降低车速、增加列车满载率及使用刚度较大的减振扣件可以对车桥振动有一定程度的改善。地铁运营管理部门须加强对地铁高架区段列车运行情况、高架桥梁结构使用状态的关注与检测,对轨道线路进行定期的维护,以确保地铁列车运行的安全性、舒适性及桥梁结构的安全稳定。
[1] 闫维明,聂晗,任珉,等.地铁交通引起地面振动的实测与分析[J].铁道科学与工程学报,2006,3(2):1.
[2] 刘卫丰,刘维宁,袁扬,等.地铁列车与道路车辆运行对环境的振动影响现场测试与分析[J].铁道学报,2013,35(5):80.
[3] 蒋通,张昕.高架轨道交通引起环境振动的实测与数值模拟[J].同济大学学报,2004,32(5):565.
[4] 夏禾,张楠,曹艳梅.列车对周围地面及建筑物振动影响的试验研究[J].铁道学报,2004,26(4):93.
[5] 陈建国,夏禾,肖军华,等.列车运行对周围地面振动影响的试验研究[J].岩土力学,2008,29(11):3113.
[6] 李小珍,刘全民,张迅,等.铁路高架车站车致振动实测与理论分析[J].岩土力学,2014,49(4):612.
[7] 陈建国,夏禾,曹艳梅,等.运行列车对周围建筑物振动影响的试验研究[J].振动工程学报,2008,21(5):476.
[8] 栗润德,刘维宁,张鸿儒.区间地铁列车振动的地面响应测试分析[J].中国铁道科学,2008,29(1):120.
[9] 刘长卿,车驰东,朱瑞仪.城市交通高架轨道振动衰减的快速预报[J].上海交通大学学报,2013,47(2):242.
[10] 魏蓬勃,夏禾,陈建国,等.高架轨道交通引起的地面振动理论与试验研究[J].工程力学,2009,26(10):117.
[11] 夏禾,郭薇薇,张楠.车桥系统共振机理和共振条件分析[J].铁道学报,2006,28(5):52.
[12] 夏禾,张楠,郭薇薇,等.车桥耦合振动工程[M].北京:科学出版社.2014.
[13] 翟婉明,夏禾.列车-轨道-桥梁动力相互作用理论与工程研究[M].北京:科学出版社.2011.
[14] ZHANG N,ZHOU S,XIA H,et al.Valuation of vehicletrack-bridge interacted system for the continuous CRTII nonballast track slab[J].Science China:Technological Science,2014,57(10);1895.

