简支曲线梁桥中预应力引起扭矩的计算分析

董 鹏

（上海市政工程设计研究总院（集团）第六设计院有限公司,安徽 合肥 230001）

0 引言

近年来，在大型立交设计中，对于空间的要求越来越严格，因此大跨度的预应力混凝土曲线梁桥得到了更多的应用。曲线梁在预应力的作用下，受力复杂，且具有弯扭耦合效应，预应力的空间分析存在一定的困难[1]。目前，学术上的研究热点是预应力的等效荷载和曲线梁桥的求解理论，对预应力的影响仅仅进行了定性分析。本文将以简支曲线梁为研究对象，采用经典的力学分析，推导出预应力引起的扭矩计算公式，为立交桥的设计提供参考和依据。

1 扭矩公式的推导

1.1 预应力的等效荷载

预应力对曲线梁桥的作用效应可以用6个个均布荷载来等效，分别是径向，切向和竖向3个方向上的均布力和均布力矩[2]。在实际的设计中，预应力筋与截面剪心的横向相对位置一般是不变的，每个腹板的配束也是大致相同的，因此，6个均布荷载可以简化为3个，即沿着竖向和径向的均布力以及径向均布力引起的均布扭矩，见式（1）～式（3）。

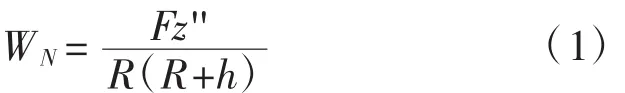
式中：WN、WM为分别代表竖向和径向的均布力；QL为指向切向的均布力矩；F为预应力的张拉力；R为曲线梁桥的曲率半径；h为预应力与横断面剪切中心的水平距离；z为预应力与横断面剪切中心的垂直距离。

预应力的竖向均布力WN可以抵抗部分外荷载，径向均布力WM则会产生不利于结构受力的扭矩，但是WN因弯扭耦合作用能减小一部分扭矩。从式（3）可知，预应力引起的扭矩与z有关，因此首先求解z与截面位置的关系。

1.2 预应力筋线形方程的确定

实际设计中，预应力的线形通常有两种基本形式，一种是不同斜率的直线用圆曲线内插相接，这种线形简洁实用，应用广泛；另外一种是二次抛物线，它有着固定不变的曲率，在连续体系结构中应用较多。本文以二次抛物线线型为研究对象，推导预应力产生的扭矩公式。如图1所示，x表示的是各截面剪切中心的连线。

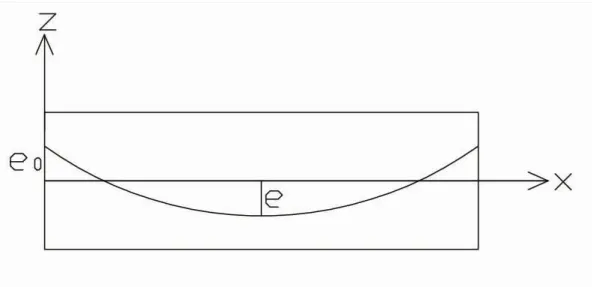
图1 立面布置图

经计算得到z与截面位置x的关系式为：

如图2所示，x与az的关系为：

由式（4）、式（5）可得 z与圆心角 az的关系

式中：αz为曲线梁桥x处所对应的圆心角，rad；L为曲线梁桥的桥长，m；e0、e为梁端及跨中预应力筋与剪心的竖向距离，m。

1.3 扭矩公式的推导

立交桥的桥长远大于桥宽，适用于单纯扭转理论，采用结构力学的方法可以得到精确的解析解[3]。简支曲线梁桥主要采用的是抗扭双支座，是一次超静定结构，见图2，超静定曲线梁桥的力法方程为：

图2 简支曲线梁桥示意图

式中：δBB为单位扭矩TB=1作用下基本体系在支座B处的扭角；TB为简支梁桥支座B处的扭矩；ΔBT为预应力引起的扭矩在支座B处引起的扭角。

求解力法方程得到的扭矩计算公式为：

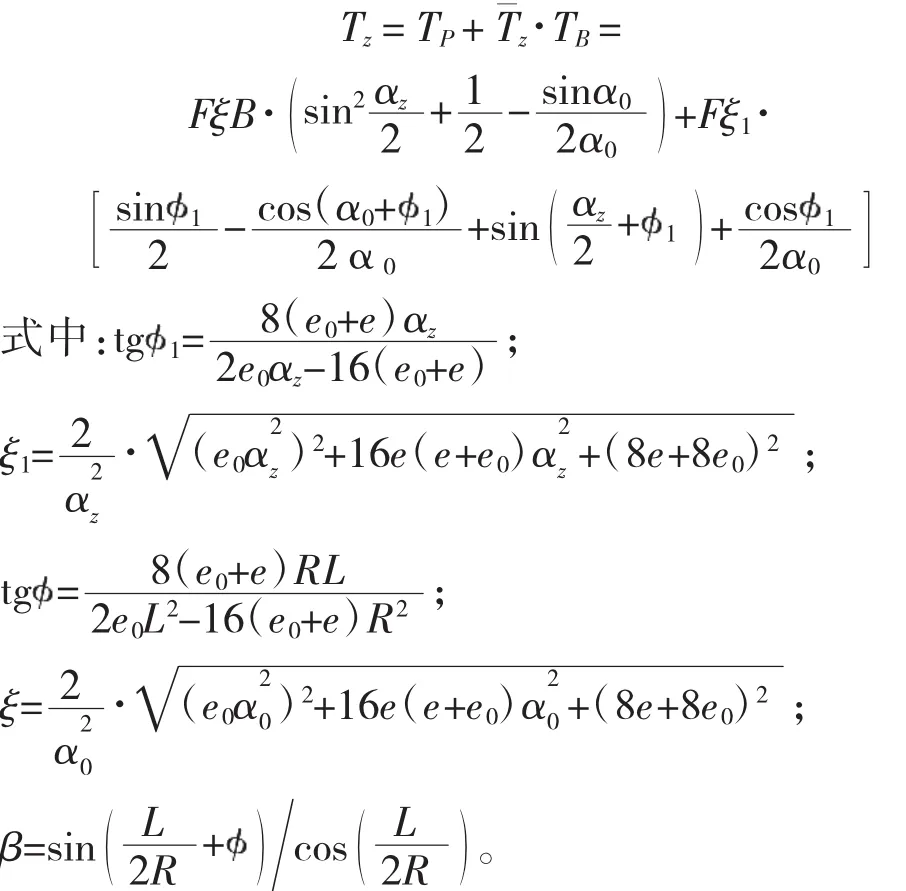
1.4 扭矩公式的简化

上述推导了预应力引起扭矩的计算公式，但是计算过程比较复杂，为了更好的应用于工程设计，需要对公式进行简化。将预应力引起的扭矩等效换算成均布扭矩，就可以利用《曲线梁》[2]里的计算公式，进一步的简化计算公式，计算简图见图3。

图3 预应力引起扭矩的计算模型

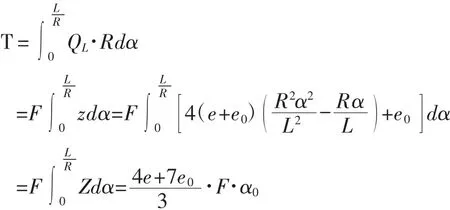
则预应力径向力的等效均布扭矩为：

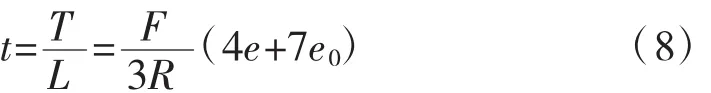
曲线梁桥中竖向均布力和均布扭矩作用下的扭矩公式[2]为：

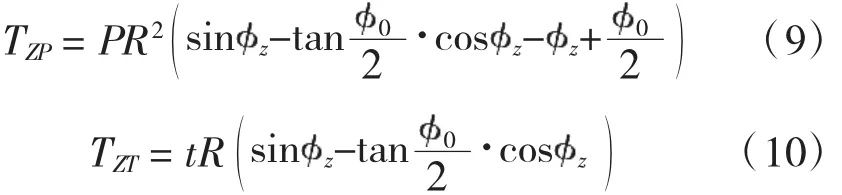
由式（6）可得

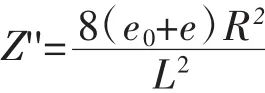
将其化入到式（1），得二次抛物线形的竖向均布荷载为：

将式（11）代入到式（9），得到竖向荷载因弯扭耦合引起的扭矩：

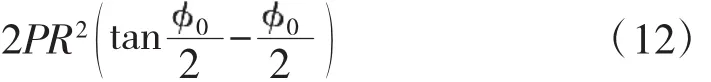
结合式（8）、式（12）得到预应力实际引起的等效均布扭矩：

式（13）代入到式（10）可得预应力引起的扭矩计算公式。

2 公式验证

采用Midas/Civil空间有限元软件，建立一个实际模型，为了简化计算，将实际模型中的钢束简化为2根对称布置的预应力筋进行分析，对比两种情况下预应力引起的扭矩值，结果见表1。

从表1可以看出，软件值与公式值的误差最大为3.8%，均不超过5%，满足工程实际的需要。而且桥梁的长宽比越大，结果就越精确。根据曲线梁桥的受力特点，预应力作用下的跨中扭矩为0，故不再与软件对比，公式的计算值为0。

3 结语

根据上述研究，可得以下认识：

（1）简化后的扭矩公式满足工程设计上的需要，可以广泛的用于分析预应力对简支曲线梁桥扭矩的影响。

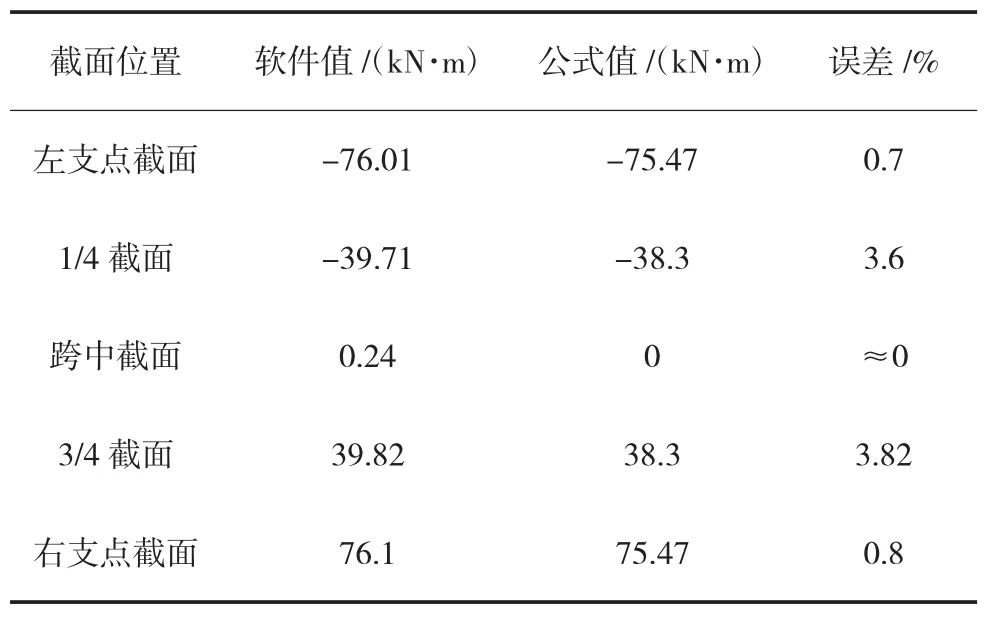
表1 软件值与公式值的对比

（2）公式主要用于分析桥长远大于桥宽情况下的简支曲线梁桥，一般认为长宽比至少大于4。

（3）对于直线与圆曲线相结合的线形，可以分别建立线形方程，按照式（3）直接积分计算。

参考文献:

[1]邵容光,夏淦.混凝土弯梁桥[M].北京:人民交通出版社,1996.

[2]任茶仙,竺润祥.连续曲线箱梁预应力效应分析[J].工程力学,2000(4):140-141.

[3]姚玲森.曲线梁[M].北京:人民交通出版社,1989.