考虑土-桥台-上部结构相互作用的曲线桥抗震性能研究

焦驰宇， 鲁子明， 龙佩恒， 时晓鹏， 侯苏伟,4

(1. 北京建筑大学 未来城市设计高精尖创新中心，北京 100044； 2. 北京建筑大学 工程结构与新材料北京高等学校工程研究中心，北京 100044； 3. 同济大学 土木工程防灾国家重点实验室，上海 200092； 4. 北京建筑大学 北京节能减排关键技术协同创新中心，北京 100044)

近年来，国内外发生的多次地震灾害，其中桥梁破坏受损严重，桥台震害尤其严重。如图1所示，1976年唐山地震(M7.8)中，某铁路桥桥台受到地震影响，桥址处场地砂土液化，造成桥台周围填土滑移，致使桥台发生破坏[1]；1994年美国Northridge地震(M6.7)中，受损的桥梁中一半以上的桥梁出现了桥台震害。图2所示为一座10跨曲线箱梁桥，地震时主梁与桥台碰撞，造成桥台侧墙破坏,主梁也因失去了桥台的支撑约束，而背离桥台移动了150 cm[2]。从上述可以看出，桥台破坏主要原因是地震中土-桥台-上部结构相互作用。

图1 桥台台后路基塌陷 Fig.1 Abutment subgrade subsidence

图2 桥台挡块破坏(Northridge地震，1994年) Fig.2 Shear key failure of Abutment (Northridge earthquake,1994)

Aviram等[3-4]对直线桥梁考虑土-桥台-上部结构相互作用的抗震性能做了相关研究；彭大文等[5]对于整体式桥台桥梁进行了天然脉动荷载作用下的自振特性的研究；李悦等[6]提出了一种考虑土-桥台-上部结构相互作用的离散质点-弹簧模型，并对其进行了一些非线性抗震研究；Wieser等[7]探讨了曲线桥在桥台-主梁相互作用下的抗震性能；高玉峰等[8]在前人研究基础上推导出了考虑土的非线性及桥台高度修正的桥台刚度计算公式；李立峰等[9]探讨了桥台-填土-结构相互作用对于直线桥抗震性能的影响。但对于曲线桥中考虑土-桥台-上部结构相互作用的抗震性能国内外鲜有研究。因此本文以某曲线桥为工程背景，考虑桥台-土-结构相互作用，通过改变曲率半径、桥台模拟等方法，建立不同的桥梁有限元模型进行研究，以期对曲线桥梁的抗震性能进行相关研究。

1 建立模型

1.1 工程背景

本文拟采用工程背景为某公路互通式立交桥G匝道桥。该桥上部结构为现浇5×33 m预应力混凝土连续弯箱梁(R=165 m)，桥梁全宽8.5 m，行车道宽7.0 m，墩柱高14 m。全桥结构如图3(a)、图3(b)所示，桥台为肋板式桥台，如图3(c)所示。桥台分为起点桥台、终点桥台，1#、4#桥墩为边墩，2#、3#桥墩为中墩。桥台采用板式橡胶支座(GYZØ400×84 mm)连接，桥墩与主梁刚性连接。下部结构为独柱式桥墩，基础采用钻孔灌注桩。桥址处为III类场地土。

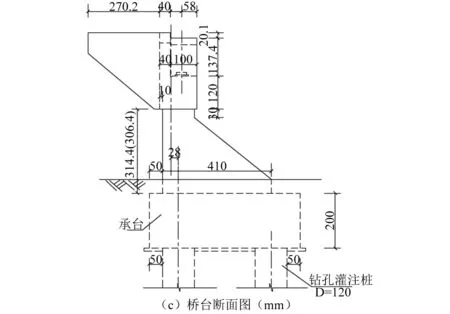
图3 桥梁基本信息图 Fig.3 Basic information map of bridge

1.2 数值模拟方法

已有研究表明：使用大型有限元模拟软件，对全桥建立精细化数值模型，可以考虑非线性影响获得对桥梁地震反应的详细认识。据此，本文建立了三维有限元模型，主梁顺桥向为X轴，横桥向为Y轴，竖向为Z轴，墩柱顺桥向为Y轴，横桥向为Z轴，竖向为X轴。由于桥宽较窄，主梁、墩柱、单桩采用三维空间梁单元模拟，沿桩身施加等代弹簧方式模拟桩侧土对单桩的弹性作用。

为获得真实的地震反应，本文参阅Aviram的文章，选择四种模拟方法(见表1)对土-桥台-上部结构相互作用进行了精细化数值模拟。同时，已有研究表明：在地震作用下，曲线梁桥墩柱将会发生弯扭耦合破坏，而曲率半径是影响地震反应的重要因素。据此，本文选用曲率半径分别为45 m、200 m、500 m的三种曲线桥进行研究，具体如下一节所示。

1.2.1 简化桥台模型

根据Aviram文中所述，简化桥台模型由一个长度为Dw的刚体单元构成(Dw为上部结构宽)，通过刚性连接到已经定义的上部结构纵向中心线，并在每一端采用纵向、横向和垂直方向的弹簧单元连接考虑非线性动力响应影响。在纵向，定义了一个串联体系，其中刚性杆释放了剪力和弯矩，两边都有一个间隙单元作为边界条件来约束，如同零长度的刚体单元，只允许纵向运动，如图4所示。在横桥向，采用接触单元模拟[10]了主梁与桥台挡块之间的横向相互碰撞，如图5所示。整个桥台模型如图5所示。

表1 桥台模拟方法汇总表Tab.1 Abutment simulation method summary

图4 碰撞模拟 Fig.4 Model of collision

其关系式为：

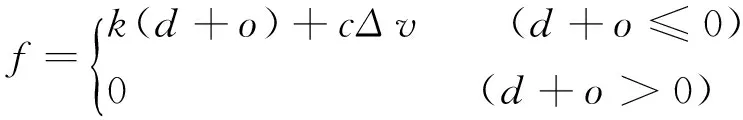
式中：d为N1、N2两点之间的相对位移，k为发生碰撞后间隙单元的轴向位移刚度，c为阻尼系数，Δv为相对速度。通过能量守恒定律可知阻尼系数c与恢复系数e的关系为：

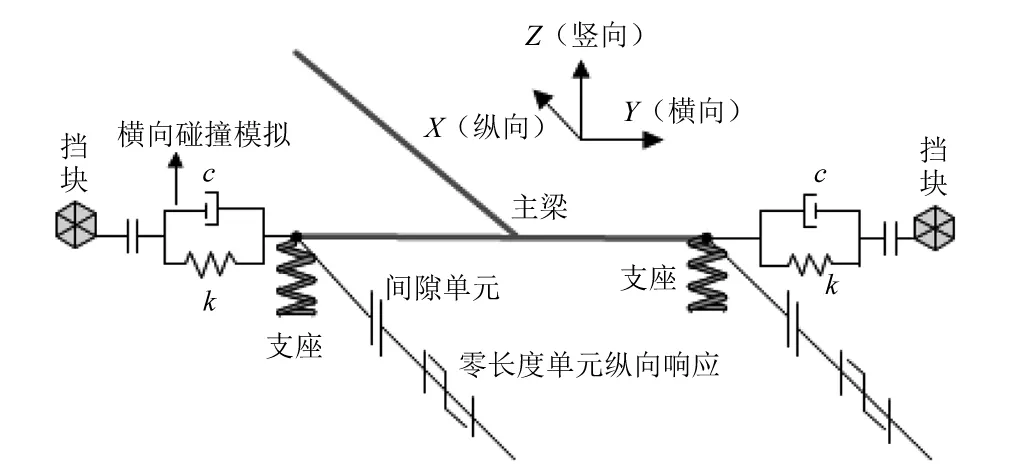
图5 简化桥台模型方案示意图 Fig.5 Schematic of simplified abutment

图6 横向碰撞模型图 Fig.6 Model of transverse collision

依据上面所做介绍，利用MIDAS/civil建立了曲率半径为45 m、200 m、500 m三种曲线桥的简化桥台模型，如图7～图9所示。简化桥台模拟如图10所示。

图7 曲率半径45 m模型 Fig.7 Model of radius 45 m

图8 曲率半径200 m模型 Fig.8 Model of radius 200 m

图9 曲率半径500 m模型 Fig.9 Model of radius 500 m

图10 简化桥台模拟情况 Fig.10 Simplified abutment simulation

由于这类模型在横向上忽略了挡块的横向约束和桥台处支座的分布。竖向上，在刚体单元两端施加线性弹簧约束，用来模拟地震作用下支座竖向响应及台后填土对桥台的相互作用影响，刚度为桥台支座刚度kv。在抗震分析中，不考虑支座和路基的竖向刚度影响，并假定土壤已完成沉降，双方按刚性条件考虑。

1.2.2 弹簧桥台模型

弹簧桥台模型由长度为Dw的刚体单元1和刚体单元2构成(Dw为上部结构宽)，刚体单元1中点通过刚性连接到上部结构纵向中心线。刚体单元2中点设置节点质量，质量大小为桥台参与质量，其算法具体见文献[11]所示。刚体单元1与刚体单元2之间通过弹簧单元相连接，以模拟板式橡胶支座。刚体单元2两端连接6个非线性弹簧支撑，其中纵向弹簧边界条件设置4个节点，第1个节点与第2个节点之间应用一个刚度较大的单元连接来模拟台背填土、背墙和桩的纵向弹性效应，并且释放此单元远离桥梁方向的约束，第2个节点与第3个节点之间采用间隙单元连接模拟桥台与主梁之间的间隙。第3个节点与最后一个节点之间采用弹簧单元连接模拟台后填土的弹性效应。在横向上，模拟主梁与挡块碰撞作用的方法与上节类似。模型示意图如图11所示。

其中，支座(GYZØ400×84 mm)抗推刚度和竖向刚度计算公式为

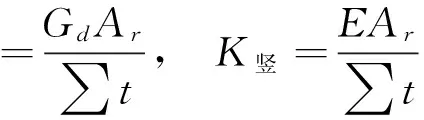
根据文献[12]表1及上述公式计算得到支座抗推刚度4 174 kN/m，竖向刚度2 138 379 kN/m。

图11 弹簧桥台模型示意图 Fig.11 Schematic of spring abutment

参考Zhang等的论文可知，路堤土体的参与质量，确定方法如下：

由公式[13]

转化，可得

式中：m为桥台与土体的参与质量，T为桥台与土体横向自振周期，一般取T=0.7 s[14]，K为桥台刚度，可由《SDC—2004》规范第七章中方程7.43和7.44计算得出。

依前所述建立三种曲率半径的曲线桥模型，如图12～图14所示。弹簧桥台模拟如图15所示。

图12 曲率半径45 m模型 Fig.12 Model of radius 45 m

图13 曲率半径200 m模型 Fig.13 Model of radius 200 m

图14 曲率半径500 m模型 Fig.14 Model of radius 500 m

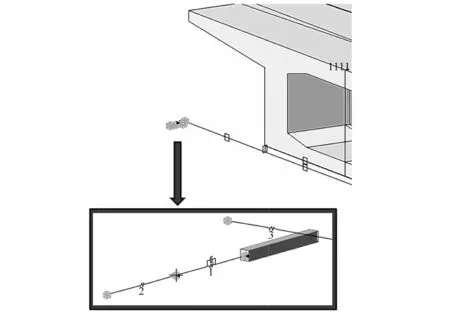
图15 弹簧桥台模拟情况 Fig.15 Spring abutment simulation

1.2.3 弹性单元桥台模型

桥台-土-结构相互作用是一个复杂的非线性问题，前面两种桥台模拟方法虽然建模简单，但是均将桥台视为刚体，忽略了桥台本身对结构在地震作用下的影响，因此本文尝试采用弹性单元建立肋板式实体桥台，土质条件为场地III类土。考虑桥台与主梁的横向接触碰撞，具体见小节1.2.1。

(1) 基本假定

① 深度方向上，土层处于平面应变状态。

② 桩周土体服从虎克定律的弹性体，将土体等效为一根两端具有支撑点没有质量的土弹簧；主、被动区的土弹簧系数变化只与软基处理和路堤填筑有关，其中土弹簧都为线性弹性；桩假定为弹性梁。

③ 土体始终处于受压状态，当土弹簧的长度大于受初始压力时的计算长度时，取土弹簧长度为原始长度，即土体不能受拉力作用。

④ 在研究中，桩、桥台桩除了受软基处理和路堤填筑的影响外，不考虑其他水平方向外力的影响因素和位移变化等。

(2) 模拟方法

桥台的盖梁、挡块及桩基础采用“梁单元”模拟，肋板、承台采用“板单元”模拟，厚度分别为1 m、2 m。在桥台台背、肋板及桩身上添加“土弹簧”,“土弹簧”刚度计算采用我国公路桥涵地基与基础设计规范[15]用的“m法”计算。

据此，建立有限元模型如图16～图18所示。桥台模拟情况如图19所示。

图16 曲率半径45 m模型 Fig.16 Model of radius 45 m

图17 曲率半径200 m模型 Fig.17 Model of radius 200 m

图18 曲率半径500 m模型 Fig.18 Model of radius 500 m

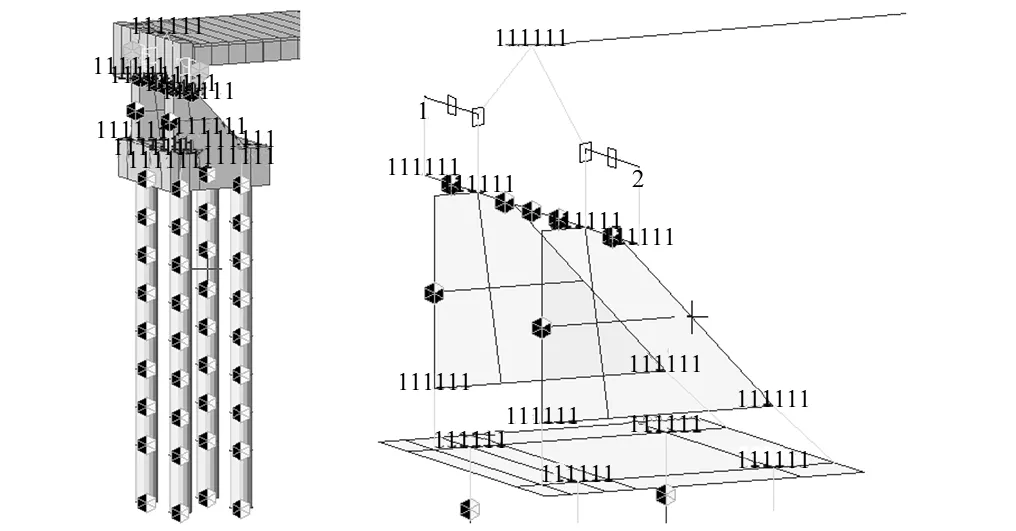
图19 弹性单元桥台模拟情况 Fig.19 The elastic element simulation of abutment

1.3 地震波输入

该桥地处III类场地，烈度为8度。利用罕遇地震下规范反应谱生成3条人工地震波，加速度时程曲线如图20所示。其峰值为4.066 m/s2。地震波输入方向取两端桥台连线方向[16]。

2 两种因素对结构抗震性能影响

本文首先在考虑恒载的基础上对结构进行非线性时程反应分析，取3条时程波分析结果的平均值作为比较基础。本文主要对比在相同曲率半径的情况下，不同的桥台模拟方法(滚轴桥台模型、简化桥台模型、弹簧桥台模型、弹性单元桥台模型)对于结构抗震性能

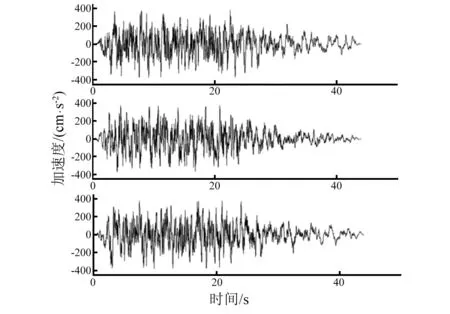
图20 人工地震波加速度与时间函数图 Fig.20 Artificial ground motion

的影响；在同种桥台模拟方法的情况下，不同曲率半径(45 m、200 m、500 m)下曲线桥的抗震性能，探究曲率半径对结构抗震性能的影响，并试图找出一种较为准确的桥台模拟方法用于结构抗震性能评价。

已有研究表明：桥梁的墩柱将主梁的恒载及地震作用传递给基础，因而墩柱为地震中的核心受力构件，所以有必要研究地震作用下墩柱内力的影响。同时，地震中梁体会产生位移，墩柱和桥台也会受地震作用影响而产生位移，两者与主梁之间存在位移差，当位移差大于支承面宽度会导致落梁现象发生。因而对比分析中，台梁、墩梁相对位移也是重点关注因素。

2.1 桥台模拟方法的影响

2.1.1 桥台模拟方法对墩柱内力的影响

选取曲率半径为200 m的曲线桥作为研究对象，通过改变桥台模拟方法来探究对曲线桥墩柱内力的影响情况。图21～图24为四种工况(滚轴桥台模型、简化桥台模型，弹簧桥台模型，弹性单元桥台模型)的墩柱内力图，包括法向剪力，切向剪力，法向弯矩，切向弯矩。选取了1-4号桥墩墩底。

图21 四工况墩底法向剪力图 Fig.21 Pier bottom normal shear diagram of conditon 1&2&3&4

从图21～图24可以看出曲线桥墩柱的法向剪力、切向剪力和切向弯矩的增减趋势大体一致，但桥台-土-上部结构相互作用对弹性单元桥台模型的边墩法向内力影响较大，未考虑桥台-土-上部结构相互作用的滚轴桥台模型中边墩的法向内力比弹性单元桥台模型中法向内力大30%左右。其原因为弹性单元桥台模型考虑土-桥台-上部结构相互作用，对桥台及边墩横向具有约束作用，所以边墩法向内力减小，从图2.1中也可看出，相比于另三种桥台模型，弹性单元桥台模型边墩法向剪力较小。

图22 四工况墩底切向剪力图 Fig.22 Pier bottom tangentialshear diagram ofconditon 1&2&3&4

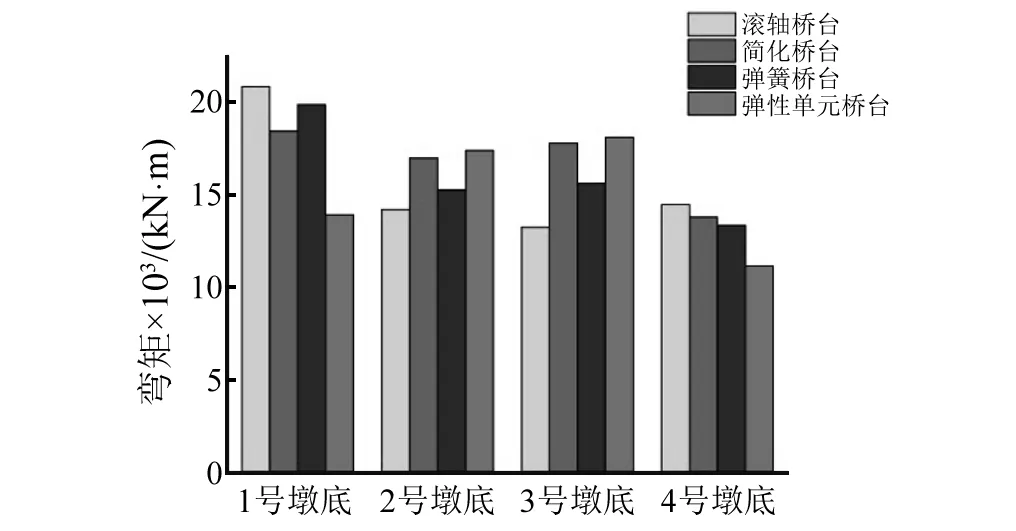
图23 四工况墩底法向弯矩图 Fig.23 Pier bottom normal bending moment diagram of conditon 1&2&3&4

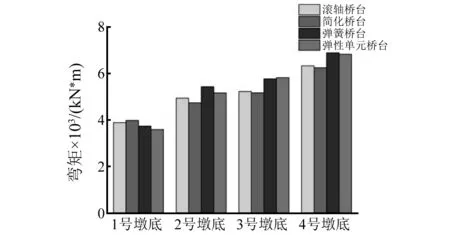
图24 四工况墩底切向弯矩图 Fig.24 Pier bottom tangential bending moment diagram of conditon 1&2&3&4

2.1.2 桥台模拟方法对墩柱与主梁相对位移的影响

选取曲率半径200 m的曲线桥作为研究对象，通过改变桥台模拟方法来探究对曲线桥梁墩梁横、纵向相对位移的影响情况。图25～图26为四种工况(滚轴桥台模型、简化桥台模型、弹簧桥台模型，弹性单元桥台模型)的横向、纵向相对位移图。选取1-4号墩墩顶4个点与主梁的相对位移。

图25 四工况横向位移图 Fig.25 Transverse displacement diagram of condition 1&2&3&4

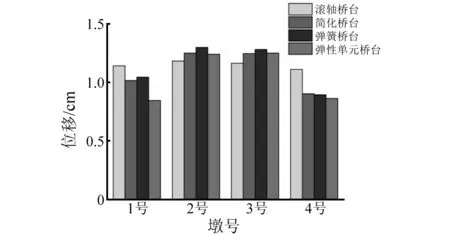
图26 四工况纵向位移图 Fig.26 Longitudinal displacement diagram of condition 1&2&3&4

从图25可以看出四种工况中墩横向位移基本一致，而边墩位移存在差异。其中弹性单元桥台模型的1号边墩位移比未考虑桥台-土-上部结构相互作用的滚轴桥台模型小28.4%，这是由于弹性单元式桥台模型考虑了桥台本身的特性，一定程度上提高了结构整体质量，致使在地震作用下距离桥台较近的边墩与主梁的相对位移较小；从图26可以看出后三种工况的中墩与边墩纵向位移量相差较大，其中弹性单元式桥台模型的中墩与边墩纵向位移相差32.4%，而滚轴桥台模型的中墩与边墩纵向位移相差很小。其原因在于考虑土-桥台-上部结构相互作用可以有效约束结构与桥墩的纵向相对位移，所以在距离桥台较近的边墩与主梁相对位移较小，较远的中墩与主梁相对位移较大。综上所述，弹性单元式桥台模拟方法可以较为真实的反映桥台在地震作用下的反应，所以本文后续选取弹性单元式桥台模拟方法来研究曲率半径对曲线桥抗震性能的影响。

2.2 曲率半径的影响

2.2.1 曲率半径对墩柱内力的影响

图27～图30为三种工况(曲率半径45 m、200 m、500 m)墩柱内力图，包括法向剪力，切向剪力，法向弯矩，切向弯矩。选取了1-4号桥墩墩底。

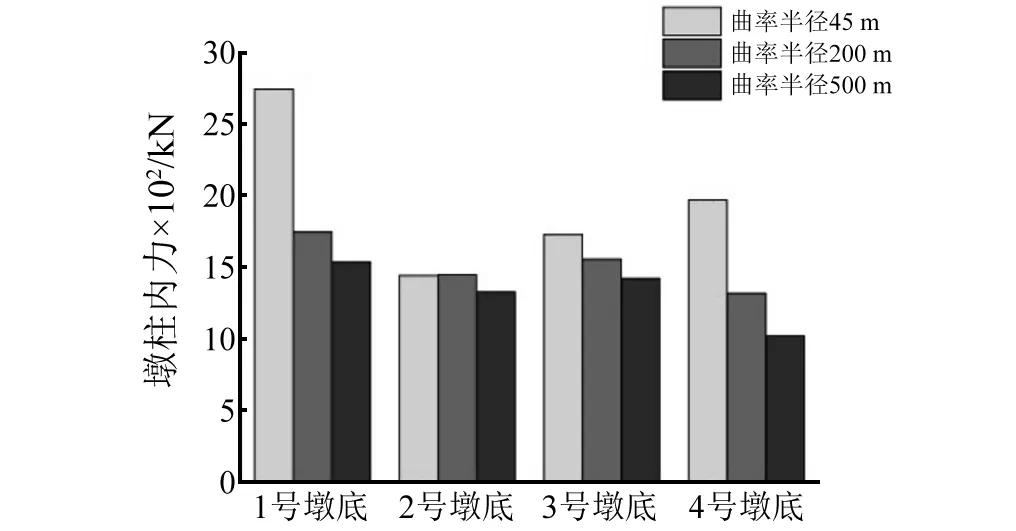
图27 三工况墩底法向剪力图 Fig.27 Pier bottom normal shear diagram of conditon 1&2&3

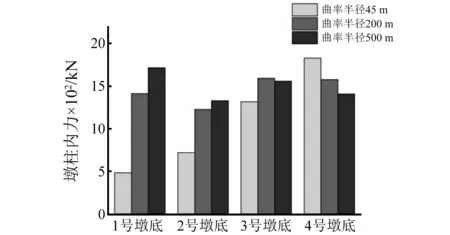
图28 三工况墩底切向剪力图 Fig.28 Pier bottom tangentialshear diagram of conditon 1&2&3

图29 三工况墩底法向弯矩图 Fig.29 Pier bottom normal bending moment diagram of conditon 1&2&3

图30 三工况墩底切向弯矩图 Fig.30 Pier bottom tangential bending moment diagram of conditon 1&2&3

从图27～图30可以看出，随着曲率半径的增大，墩柱各项内力都趋于平稳，说明曲率半径越大，桥梁墩柱受力越平均。其原因在于随着曲率半径的增加，曲线桥越接近直线桥，弯扭耦合效应减小[17]，所以各个墩柱内力分配更为平均。

2.2.2 曲率半径对桥台、墩柱与主梁相对位移的影响

图31～图32为三种工况(曲率半径45 m、200 m、500 m)相对位移图，包括横向相对位移和纵向相对位移。图中横坐标1-4号代表桥墩墩顶、0号和5号分别代表起点、终点桥台，共选取6个点与主梁的相对位移。

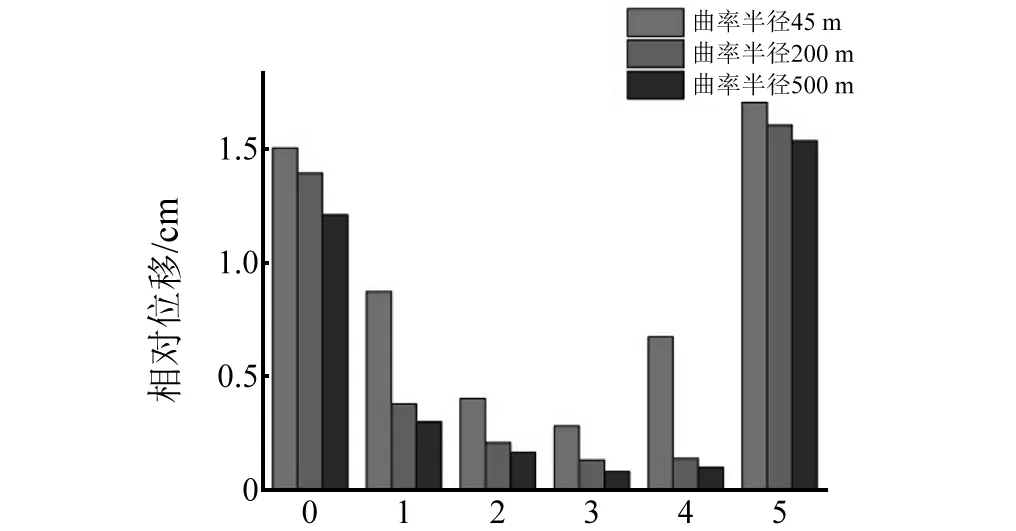
图31 两工况横向位移图 Fig.31 Transverse displacement diagram of condition 1&2

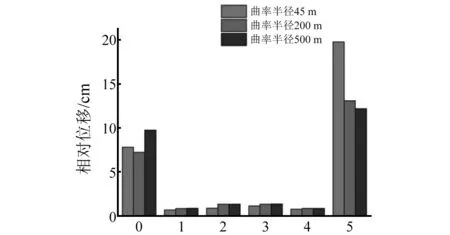
图32 两工况纵向位移图 Fig.32 Longitudinal displacement diagram of condition 1&2

从图31中可以看出，随着曲率半径的增大，台梁横向相对位移、墩梁横向相对位移都减小，就1号墩顶位移来看，曲率半径500 m模型比曲率半径200 m模型小20.7%，曲率半径500 m模型比曲率半径45 m模型小65.6%，可以看出曲率半径越小，二者差异越明显，而且边墩与主梁相对位移比中墩与主梁相对位移大。说明曲率半径对墩梁横向位移、台梁横向位移影响均较为明显。小半径曲线桥弯扭耦合效应增加，使桥梁横向位移增大，并且边墩及桥台横向位移较大，中墩横向位移较小。从图32中可以看出，墩梁纵向相对位移几乎一致，说明曲率半径的大小对墩梁纵向相对位移影响较小。

3 结 论

本文研究曲率半径对曲线桥抗震性能的影响，并试图找到一种较为准确的桥台模拟方法对曲线桥抗震性能进行评价。以某五跨曲线桥为工程背景，通过对12个模型在人工地震作用下变参数对比研究，得到以下结论：

(1) 以往的滚轴桥台模型对边墩的内力及位移计算结果有一定过量估计。与未考虑了土-桥台-上部结构相互作用的滚轴桥台模型相比，考虑了土-桥台-上部结构相互作用的弹性梁单元桥台模型对桥台及边墩的约束作用较强，在地震作用下可以有效约束边墩的位移以及内力，这使研究人员在对曲线桥进行抗震设计时对于边墩的设计有更加合理的计算依据。

(2) 曲率半径对墩梁横向位移、台梁横向位移影响均较为明显。曲率半径越小，曲线桥弯扭耦合效应增加，桥梁横向位移越大并且边墩与中墩的位移差越大；曲线桥墩柱内力分配不平均，曲率半径越小的曲线桥各个墩柱内力相差往往很大，在对曲线桥进行抗震设计时应予以重视。

[ 1 ] 何度心. 桥台抗震设计的理论与方法[J].世界地震工程, 1991, 7(3): 1-16.

HE Duxin. The theory and method of bridge abutmentseismic design [J]. Journal of World Earthquake Engineering, 1993, 7(3): 1-16.

[ 2 ] 陈张伟, 王志强, 魏红一. 桥台震害及其抗震研究综述[C]//第八届全国土木工程研究生学术论坛论文集.杭州:浙江大学出版社,2010.

[ 3 ] AVIRAM A, MACKIE K, STOJADINOVIC B. Effect of abutment modeling on the seismic response of bridge structures [J]. Earthquake Engineering and Engineering Vibration, 2008, 7(4): 395-402.

[ 4 ] AVIRAM A, MACKIE K, STOJADINOVIC B. Guidelines for nonlinear analysis of bridge structures in California [R]. 2008.

[ 5 ] 彭大文，洪锦祥，郭爱民.整体式桥台桥梁的动力试验研究[J].中国公路学报,2004, 17(4): 59-63.

PENG Dawen, HONG Jinxiang, GUO Aimin. Study on dynamic test of monolithic abutment bridge [J]. China Journal of Highway and Transport, 2004, 17(4): 59-63.

[ 6 ] 李悦，宋波，川岛一彦.考虑土、上部结构和桥台相互作用的桥台抗震性能研究[J].岩石力学与工程学报, 2009, 28(6): 1162-1168.

LI Yue, SONG Bo, KAWASHIMA K. Research on abutment seismic performance considering interaction of soil, superstructure and abutment [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(6): 1162-1168.

[ 7 ] WIESER J. Experimental and analytical investigation of seismic bridge-abutment interaction in a curved highway bridge [D]. USA, Reno, University of Nevada, 2014.

[ 8 ] 高玉峰, 蒲黔辉. 考虑碰撞效应的桥梁非线性地震反应特性研究[D]. 成都:西南交通大学, 2010.

[ 9 ] 李立峰, 王辉辉, 吴文朋. 桥台-填土-结构相互作用对RC连续梁桥抗震性能的影响分析[J].世界地震工程, 2017, 33(2): 71-79.

LI Lifeng, WANG Huihui, WU Wenpeng. Influence of abutment-soil-structure interaction on seismic performance of reinforced concrete continuous girder bridge [J]. World Earthquake Engineering, 2017, 33(2): 71-79.

[10] 聂利英, 李建忠, 范立础. 地震作用下结构碰撞的模型参数及其影响分析[J].工程力学, 2005, 22(5): 142-147.

NIE Liying, LI Jianzhong, FAN Lichu. Selection of pounding analysis parameters and its effects on structure under earthquake [J]. Engineering Mechanics, 2005, 22(5): 142-147.

[11] ZHANG J, MAKRIS N. Kinematic response functions and dynamic stiffnesses of bridge embankments [J]. Earthquake Engineering and Structural Dynamics, 2002, 31(11): 1933-1966.

[12] 中华人民共和国交通行业标准.JTT 663—2006公路桥梁板式橡胶支座规格系列[S].北京：人民交通出版社，2007.

[13] CALTRANS. Seismic design criteria [S]. California Department of Transportation, Sacramento, Califronia, 2004.

[14] MACKIE K, STOJADINOVIC B. Bridge abutment model sensitivity for probabilistic seismic demand evaluation [C]. Proc. 3rd Nat. Seismic Conf and Workshop on Bridges and Highways, Portland, Oregon, USA, 2002.

[15] 中华人民共和国行业标准.JTG D63—2007公路桥涵地基与基础设计规范[S].北京：人民交通出版社，2007.

[16] 中华人民共和国行业标准.JTGT B02—01—2008公路桥梁抗震设计细则[S]. 北京：人民交通出版社,2008.

[17] 韩星. 曲线梁桥“弯扭耦合”效应影响因素分析研究[D]. 重庆:重庆交通大学, 2014.