基于希尔伯特黄变换的高压输气管道爆裂振动信号时频特性分析

吴建源， 龙 源， 纪 冲， 李兴华， 马华源， 程良玉

(1. 75833部队，广州 510080； 2. 解放军理工大学 野战工程学院，南京 210007)

管道输送是天然气运输的主要方式之一。为提高输送效率，天然气输送管道正向高钢级、大口径、高气压规格发展。尽管大口径高压天然气具有高效、经济等特点，但由于环境腐蚀、近域施工、自然灾害及其他未知因素的影响，天然气管道断裂爆炸事故时有发生[1-4]。自20世纪80年代以来，世界范围内发生过上千起管道爆裂事故[5]。

目前，针对高压气体管道爆裂产生的空气冲击波、热辐射等危害效应，国内外学者进行了大量的理论、试验和数值模拟研究，并依据相关研究成果制定输气管道安全设计规范[6-7]。然而，对并行埋地管道而言，空气冲击波和热辐射对其影响相对较小，管道爆裂对岩土介质冲击压缩作用形成的地震波更易造成其变形破坏[8-11]。为控制管道爆裂振动安全问题，需迫切研究揭示管道爆裂地震波的形成机理、传播规律及时-频能量特性[12]。

为研究大口径高压输气管道的爆裂危害效应，本文对直径1 219 mm的X90 输气管实施了3次全尺寸爆破试验；测试了管道裂纹扩展速度、管内气体压力变化以及地表爆破振动速度，并对结果进行了分析。文中使用希尔伯特-黄变换(HHT)方法研究了管爆地震波的时间-频率-能量分布特性，揭示高压气体管道爆裂地震波的传播及衰减规律，为深入研究邻近管道和建筑物在管爆地震效应下的振动响应提供依据。

1 HHT方法的基本原理及特点

希尔伯特-黄变换(HHT)[13-15]是Huang等于1998提出的信号分析领域的一种新方法，它能够自适应地处理非平稳随机信号。对信号进行HHT分为两步：

①对信号进行经验模态分解(Empirical Mode Decomposition, EMD)，获得一系列表征信号特征时间尺度的固有模态函数(Intrinsic Mode Function, IMF)；

②对每个IMF分量作Hilbert变换获取瞬时振幅-瞬时频率-时间的分布。

EMD是利用时间序列上下包络的平均值确定“瞬时平衡位置”，进而提取固有模态函数 (IMF)。一个IMF是在给定时间所记录数据的振荡模式之一。

信号经过希尔伯特变换，可以得到信号幅值在时间-频率空间内的函数分布，即Hilbert谱

(1)

对Hilbert谱进行时间积分就得到Hilbert边际谱

(2)

边际谱是每一个频率成分幅值在时间全局上的积分，即所有幅值的累加求和。对Hilbert谱的平方进行频率积分可得到信号的瞬时能量谱

(3)

其精确地描述了信号能量随时间的变化过程。

2 试验概况

文中共设计和实施了3次(T-1、2、3)X90输气管全尺寸爆破试验。试验钢管的直径为1 219 mm，壁厚为17 mm±0.3 mm，长度为33 m(T-1和T-2)和15.3 m(T-3)。所有钢管均由超高韧性管材制成，其最小屈服强度达670 MPa，平均夏比冲击能量达294 J。

试验钢管设置在深1 m的管槽里，采用不覆土的方式爆破，管壁距离管槽边沿约20 cm。过去研究表明，要使大口径高钢级管道发生裂纹扩展，通常需在管壁轴向引入500 mm长的初始裂纹。文中采用500 mm长的线型聚能切割器在钢管中心上侧引入初始裂纹(线型聚能切割器的性能参数见表1)。

表1 线型聚能切割器性能参数Tab.1 Performance parameters of linear convergentenergy cutter

钢管爆破过程中分别使用时间线和动态压力传感器测量裂纹速度和管内气体压力变化。其中时间线由细铜丝漆包线、电阻和电源组成的简单断通电路。测量时，将漆包线缠绕在管壁上(如图1所示)，裂纹经过时，漆包线将断裂，从而产生一个断通信号。根据相邻漆包线的距离及断裂时间差，可求得裂纹经过相邻两根漆包线的平均速度。

图1 试验设置 Fig.1 Test setup

动态压力传感器沿钢管轴向安装，通过螺纹固定在管壁上。其中，T-1分别在距离钢管中心2.5 m、3.5 m、8.1 m和13.85 m的管壁环向45°位置安装一个压力传感器。文中使用的压力传感器为昆山双桥生产的CYG401压阻式高频动态压力传感器，具体技术参数如表2所示。

表2 动态压力传感器技术参数Tab.2 The technical parameters of dynamicpressure sensors

文中主要研究管道爆破引起的地震效应，考虑到安全问题所有试验均使用空气代替实际运输中的天然气。空气通过高压气泵充入管内，当达到目标压力后停止充气，3次试验的压力皆为12.3 MPa。

管道爆裂地震波采用TC-4850型测振仪进行监测，该测振仪由磁电式三矢量速度传感器和TC-4850爆破数字采集仪组成，如图2所示。三矢量速度传感器可以测试3个相互垂直方向(X-轴、Y-轴、Z-轴)的振动速度。文中把X-轴对准起爆点，Y-轴与钢管轴向平行，Z-轴垂直于地面。地震波测点主要设置在钢管垂向(V1)和钢管轴向45°(V2)，如图3所示。这样设置传感器的目的是研究管道爆裂地震波的方向特性和随传播距离的衰减特性。

图2 测振仪器的安装 Fig.2 Install vibration measurement instrument

图3 测点布设 Fig.3 Measuring point layout

3 试验结果

3.1 钢管的断裂及气体泄漏

线型聚能切割器起爆后，在聚能射流的侵彻作用下，预设位置形成贯穿裂缝(初始裂纹)。经试验后测量，贯穿裂缝的长度约为500 mm。

图4 钢管爆破过程及断裂效果(T-2) Fig.4 Pipes bursting process and cracking effect(T-2)

在T-2中，裂纹从初始裂缝两端沿轴向扩展1.75 m后，由于裂纹尖端压力的下降，发生止裂形成两条沿环向扩展的裂纹，其中一端裂纹沿环向切断钢管，另一端仍与未开裂管段连接，钢管总的开裂长度为4.0 m。除断裂长度以外，T-1和T-3中的钢管断裂情况与T-2的基本相同，其中T-1钢管断裂长度为4.6 m，T-3钢管断裂长度为2.5 m。图5所示为T-2中裂纹扩展速度随距离的变化情况。图中显示裂纹最大的扩展速度约为270 m/s，裂纹开始时扩展速度迅速增加，并在扩展约0.5 m后达到200 m/s。东侧裂纹，在扩展速度达到最大后开始下降；西侧裂纹，扩展速度不断增加，在分叉位置开始减小。T-1和T-3中裂纹扩展情况基本与T-2的类似。

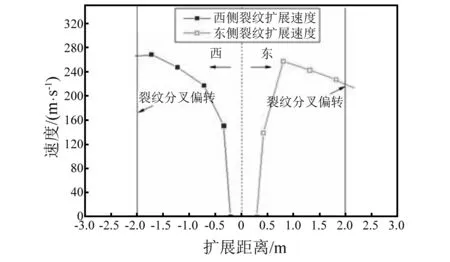
图5 裂纹扩展速度(T-2) Fig.5 Crack propagation velocity(T-2)

初始裂纹形成后，钢管两端气体泄漏速率相同。图6所示为T-1中，不同测点的压力-时间时程曲线。图中表明T-1中管内大部分气体在起爆约100 ms时已经泄漏，且距离裂口越近的位置，泄压曲线斜率越大，说明气体泄漏速度越快。过去研究表明，管内未开裂位置气体流出裂口是堵塞的，如图6所示位于裂口附近测点(距离起爆中心3.5 m)的压力在下降到约3 MPa后，压力保持不变，这个压力称为“堵塞压力”。钢管开裂后，管内气体减压波波头从断裂位置以当地声速向两侧传播，低于初始压力气体的减压波传播速度等于瞬时状态下当地声速减压气体流动的速度。从图6可以看出，切割器爆炸产生的空气冲击波，导致测点形成增压，冲击波后面的稀疏波又引起测点压力降低，在减压波波头到达前会产生多次振荡，减压波波头到达后，管道内部压力开始急剧降低。减压波波头到达4个压力测点的时间分别为6.8 ms、9.5 ms、21.9 ms和38.5 ms，根据各个测点距起裂中心的距离，可以计算得到减压波波头的传播速度约为368 m/s。

Fig.6 管内压力-时间时程曲线(T-1) Fig.6 Pressure-time traces in the pipe (T-1)

钢管爆裂对周围介质的冲击力主要与钢管断裂长度、速度和管内的初始压力相关。钢管断裂越快越长，瞬间释放的气体越多，形成的冲击力越大。同理，管内的初始压力越高，瞬间泄漏释放的能量越大，形成的冲击力也越大。

3.2 地震波测试结果

图7所示为典型的管道爆裂振动速度时程曲线，由T-1中距离钢管中心20 mV1方向上测点记录的结果。管道爆裂地震波信号表现出典型的冲击加载瞬态响应和运动特征。地震波在岩土介质中传播是复杂波动过程的合成，由于纵波、横波和面波传播速度各不相同，造成振动速度曲线出现众多峰值。从图可以看出，振动持续时间约为0.8 s。振幅衰减较快，呈现指数衰减趋势，0.5 s之后趋于平稳。根据高速摄影的观测，切割器起爆约0.5 ms后就在钢管预设位置形成初始裂缝，因此切割器爆炸作用过程小于1 ms。切割器的总装药量只有231 g，且属于裸露爆炸，其爆炸造成的振动较小。从切割器爆炸振动的作用时间和量级，结合图7的数据综合分析可知，切割器爆炸形成的振动对试验结果的分析影响不大。

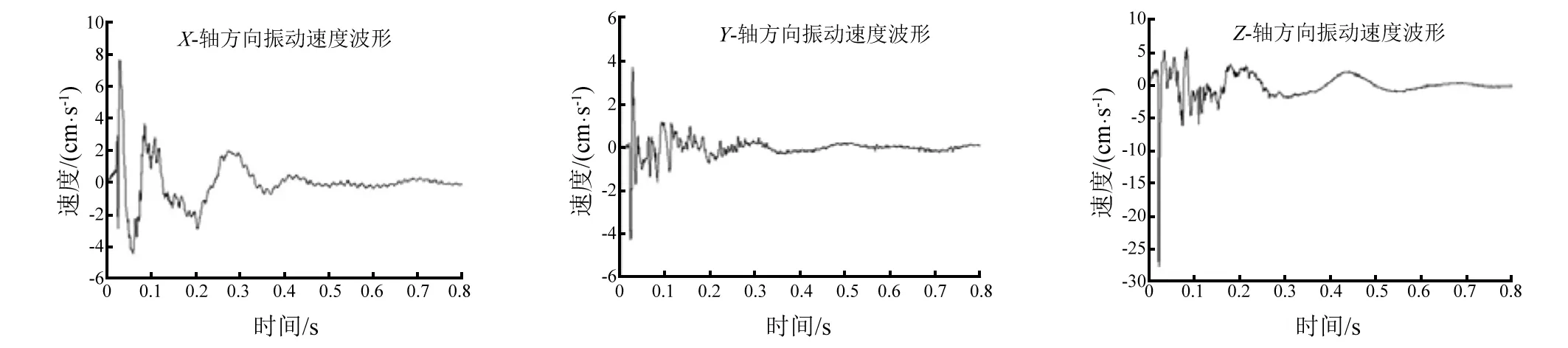
图7 T-1中距离钢管中心20 m测点(V1方向上)的振动速度时程曲线 Fig.7 The vibration velocities of measuring point 20 m away from pipe center in V1 direction (T-1)

爆破中该测点振动持续时间约为0.8 s，且Z-轴(垂直地面方向)的振动速度峰值最大，X-轴(即爆源与测点连接方向)次之，Y-轴的最小。地震波振动速度峰值出现在0.02～0.04 s之间，此时管内减压波波头尚未到达钢管端部，表明试验钢管的长度足够研究管道爆裂地震波的强度。输气管道爆裂对周围介质的冲击作用主要在断裂阶段。裂纹停止时，裂口压力开始下降直至稳态泄漏，此时泄漏气体对周围介质形成持续的作用力，但造成振动响应较小。

图8 振动速度峰值随传播距离的变化 Fig.8 The peak vibration velocity VS distance

图8所示为不同传播方向上的振动速度峰值随传播距离的变化。分析这些数据我们可以得出以下结论：①除个别奇异数值外，3次试验的振动速度峰值衰减规律基本一致。② 随着传播距离的增加，地震波的振动速度峰值随之衰减。在距离爆源约40 m以内，地震波振动速度峰值衰减较快。③ 总体来看，在同一个测点Z-轴的振动速度峰值最大，X-轴的次之，Y-轴的最小。④传播距离相同时，V1方向上测点的振动速度峰值比V2方向的大。⑤相同的测点位置，T-3的振动速度峰值普遍比T-1和T-2中的小，造成这种现象的主要原因是T-3中钢管的断裂长度比T-1和T-2的短。断裂长度越短，瞬间释放的气体量越小，形成的反作用力越小。

4 记录数据的HHT分析

4.1 低频脉冲状(LFPL)信号的提取

如图7所示，记录的数据含有低频脉冲状(LFPL)信号和高频信号。过去研究表明[16]，LFPL信号整合包括主导低频成分以及它们的峰值幅度等蕴含在地面运动的重要信息。在记录数据中筛选出LFPL波信号，并求出其在时间-频率上的能量分布特征将有助于研究震源的形成机理和土壤的非线性响应，以及量化LFPL在结构物上的影响。

HHT可以通过几个IMF分量有效地揭示LFPL波信号特征。图9所示为由EMD从原始数据分解出来的10个IMF分量，图10所示为与各分量对应的傅里叶振幅普。大多数地震数据只需分解为10个左右的IMF分量，这说明END具有较高的效率。如图9和图10所示，每个分量具有不同的振幅和频率成分。从IMF1到IMF10，分量的频率越来越低，波长也越来越长。IMF1～IMF6的持续时间约为0.2 s，而IMF7～IMF10一直持续到地震波结束，约为0.8 s。由于IMF分量在HHT中是自适应分解的，高频成分和低频成分并没有明确的界限，故在前面的IMF分量中可以发现一些低频成分。

图9 图7中Z-轴振动信号的IMF分量 Fig.9 IMF components of vibration signal (Z-axial) depicted in Fig.7

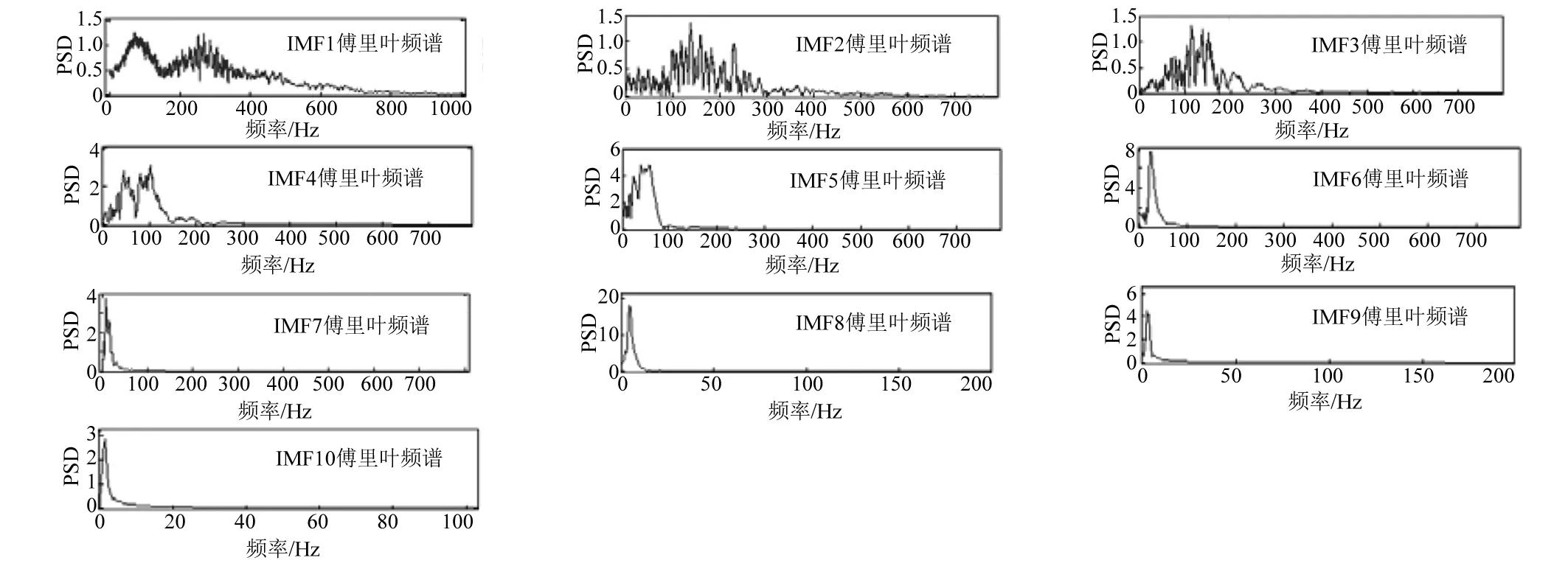
图10 图9中IMF分量的傅里叶频谱 Fig.10 Fourier spectra of the IMF components depicted in Fig.9

图11所示为基于EMD分解的低频成分和高频成分与原始数据的对比。图中基于EMD的低频成分是由IMF4～IMF10之和组成；高频成分由IMF1～IMF3之和组成。从图中可知，基于EMD分解的成分能够捕获数据中的LFPL波信号。

图11 基于EMD分解的低频成分和高频成分与原始数据的对比 Fig.11 Original data versus EMD-based low-frequency and high-frequency component

4.2 Hilbert时频能量谱

我们仍然对图7中的信号进行分析。经由EMD分解得到的IMF分量，代入希尔伯特变换后，即可得到信号的希尔伯特谱(时频能量谱)，以时频谱为研究对象，便可对数据进行清晰的时频分析。图12所示为不同振动方向上信号的Hilbert能量谱，它精确表明了各IMF分量的能量分布。从图中可以发现3个方向振动速度的希尔伯特谱整体形式基本相同，具有以下特征：①地震波到来后的0.1 s内，频率成分十分复杂，在0～150 Hz均有分布；②低频成分持续时间长，3个方向的能量谱都存在0～10 Hz的低频成分持续到地震波结束。

图12 图7中所描述信号的希尔伯特谱 Fig.12 Hilbert spectrum of the signals depicted in Fig.7

图13和图14分别为3个信号的边际谱和瞬时能量谱。对比它们的边际谱可以发现，3个方向振动的频率成分有重叠的部分但同时又存在一些差别。在0～20 Hz频率范围都具体较大的振动能量。但在这一范围X-轴的能量最大，Z-轴次之，Y-轴最小，说明X-轴的低频成分要比Y-轴和Z-轴要多。造成上述现象的原因是X-轴的振动信号是由勒夫波和瑞利波叠加产生，成分复杂。当频率大于20 Hz时，Z-轴的能量最大。

图13 信号边际谱 Fig.13 Marginal spectrum

图14 信号瞬时能量谱 Fig.14 Instantaneous energy spectrum

从瞬时能量谱可以看出，管道爆裂地震波在开始时表现出典型的冲击加载瞬态响应和运动特征。3个方向振动能量波峰出现的时间相差不大。开始时Z-轴的能量最大，但0.1 s后X-轴的能量超越Z-轴的能量。造成这种现象主要是由于Z-轴含有的高频成分能量较多，能量衰减较快，而X-轴含有的低频成分较多，能量衰减较慢。Y-轴的能量最小。由于结构物的固有频率一般较低，当爆破振动能量分布趋于低频带时容易引发结构物共振而加剧破坏。因此，通过HHT方法可以快速准确地获取管道爆破振动信号中，不同频率成份对周围结构物的影响，并用以指导管道安全设计。

5 结 论

本文通过对天然气输送管道实施3次全尺寸爆破试验，研究了管道爆破产生地震波的强度及其传播特性；分析了管道断裂、气体泄漏及地震波形成之间的内在联系；并使用HHT对管道爆裂地震波的时间-频率-能量分布特性进行了研究。最终得到以下结论：

(1) 输气管道爆裂对周围介质的冲击作用主要在断裂阶段，且断裂越快越长，瞬间释放的气体越多，形成的冲击振动越强。

(2) 地表振动速度峰值随传播距离增加而衰减，且距离爆裂中心40 m以内衰减速度较快；同一测点Z-轴的振动速度峰值最大，X-轴的次之，Y-轴的最小；V1方向上测点的振动速度峰值比V2方向的大，说明管道爆裂地震波的能量在地表上传播具有明显的方向性。

(3) 管道爆裂地震波在开始的0.1 s内，频率成分十分复杂，在0～150 Hz均有分布；其低频成分持续时间长，同一测点3个方向的能量谱都存在0～10 Hz的低频成分持续到地震波结束；总体来看，管道爆裂地震波的能量优势频段为0～20 Hz。

[ 1 ] WANG H, DUNCAN I J. Likelihood, causes, and consequences of focused leakage and rupture of US natural gas transmission pipelines[J]. Journal of Loss Prevention in the Process Industries, 2014, 30: 177-187.

[ 2 ] LOWESMITH B J, HANKINSON G. Large scale experiments to study fires following the rupture of high pressure pipelines conveying natural gas and natural gas/hydrogen mixtures [J]. Process Safety and Environmental Protection, 2013, 91(1): 101-111.

[ 3 ] LEIS B N, ZHU X K, FORTE T P. New approach to assess running fracture arrest in pipelines [C]// Pipeline Technology Conference, Ostend, 2009: 12-14.

[ 4 ] EIBER R, BUBENIK T, MAXEY W. Fracture control technology for natural gas pipelines[M]. Arlington: Technology for Energy Pipelines, 1993.

[ 5 ] 郑远攀,苏晓珂,刘新新,等. 气相井喷的泄漏源模型及其仿真[J]. 高压物理学报, 2012(2): 189-198.

ZHENG Yuanpan, SU Xiaoke, LIU Xinxin, et al. Study on leakage model of gas blowout and its numerical [J]. Chinese journal of high pressure physics, 2012(2): 189-198.

[ 6 ] DONG Gang, XUE Lin, YANG Yun, et al. Evaluation of hazard range for the natural gas jet released from a high-pressure pipeline: A computational parametric study [J]. Journal of Loss Prevention in the Process Industries, 2010, 23(4): 522-530.

[ 7 ] 李伟,张奇. 高压氢气输运装置物理爆炸状态场特征及灾害效应研究[J]. 高压物理学报, 2009(3): 203-208.

LI Wei, ZHANG Qi. Study on the physical explosion character and ejection effect of the high-pressurized hydrogen transport device [J]. Chinese journal of high pressure physics, 2009(3): 203-208.

[ 8 ] 许砚新，马学海，庞宝华，等. 天然气管道与原油管道并行敷设的安全间距[J]. 油气储运，2011, 30(11): 816-818.

XU Yanxin, MA Xuehai, PANG Baohua, et al. Determination of safety distance for parallelly laid natural gas/oil pipelines. Oil & Gas Storage and Transportation, 2011, 30(11): 816-818.

[ 9 ] ACTON M R, JACKSON N W, JAGER E E R. Development of guidelines for parallel pipelines [C]// 2010 8th International Pipeline Conference. American Society of Mechanical Engineers, 2010: 485-495.

[10] 赵燕辉,吴明,张纯静. 油气管道并行敷设技术研究现状[J]. 节能技术, 2012, 30(9): 447-450.

ZHAO Yanhui, WU Ming, ZHANG Chunjing. Research status in parallel laying technology of oil and gas pipelines [J]. Energy Conservation Technology, 2012, 30(9): 447-450.

[11] SU Huayou. Analysis of characteristics of compound vibration and effects to surrounding gas pipeline caused by impact and explosion [J]. Procedia Engineering, 2011, 26: 1835-1843.

[12] 路亮,龙源,谢全民,等. 爆破振动信号的提升小波包分解及能量分布特征[J]. 爆炸与冲击, 2013(2): 140-147.

LU liang, LONG Yuan, XIE Quanmin, et al. Decomposition and energy distribution of blasting vibration signal based on second generation wavelet packet [J]. Explosion and Shock Waves, 2013(2): 140-147.

[13] ZHANG R R, MA S, SAFAK E, et al. Hilbert-Huang transform analysis of dynamic and earthquake motion recordings [J]. Journal of Engineering Mechanics, 2003, 129(8): 861-875.

[14] HUANG N E, WU Z. A review on Hilbert-Huang transform: Method and its applications to geophysical studies [J]. Reviews of Geophysics, 2008, 46(2): 1-23.

[15] 刘翠伟,李玉星,孟令雅,等. 基于希尔伯特黄变换的输气管道泄漏音波时频特性分析[J]. 振动与冲击,2014, 33(16): 42-49.

LIU Cuiwei, LI Yuxing, MENG Lingya, et al. Time-frequency analysis of acoustic leakage signal for natural gas pipelines based on Hilbert-Huang transform [J]. Journal of Vibration and Shock, 2014, 33(16): 42-49.

[16] ALAVI B, KRAWINKLER H. Consideration of near-fault ground motion effects in seismic design [C]// Proceedings of the 12th World Conference on Earthquake Engineering, 2000.