蘑菇头对铜底吹炉内气液流动影响数值模拟研究
王书晓, 余 跃, 温 治, 刘训良
(1.中国恩菲工程技术有限公司, 北京 100038; 2.北京科技大学能源与环境工程学院, 北京 100083)
0 引言
氧气底吹熔池熔炼工艺是我国有色冶金领域研究人员研发的先进冶炼新工艺[1-2],具有原料适应性强、能耗低等优点。富氧空气通过炉底喷枪喷入炉内,作为冶炼反应物的同时并搅拌熔池内熔体,底吹炉内包含复杂的多相流动行为,熔池气泡对炉内熔炼效果有着重要影响;底吹气体较高温熔体温度很低,高温熔体会逐渐在氧枪喷口周围形成蘑菇状的疏松多孔介质区,称为“蘑菇头”。实际冶炼中,合适大小的蘑菇头,既不妨碍送气量,又可保护氧枪;但蘑菇头的存在亦会对气体喷吹和气液流动产生影响。
上世纪90年代以来,为延长底吹喷嘴和炉底内衬寿命,部分冶金工作者[3-6]对顶底复吹转炉炼钢过程中形成的蘑菇头进行了研究,并取得了一些研究成果。认为底吹气体流量的平方根与蘑菇头的半径成正比,底吹气体流量与喷枪供气压力成正相关,在一定范围内,底吹喷枪供气压力较大时有助于蘑菇头的形成。这些研究使人们对蘑菇头的组织结构和形成机理有了初步了解,但受限于当时的技术条件等,研究并不深入,也不连续。另一方面,铜底吹炉与顶底复吹转炉有相似之处的同时,也存在区别,而目前关于铜底吹炉内氧枪出口端蘑菇头方面的研究鲜有报道。
数值模拟方法与传统试验研究方法相比,具有安全可靠、信息全、成本低、方便快捷等优点,已成为研究冶金炉窑内高温流体多相流动的重要方法。Li[7]、Yu[8]、闫红杰[9]等学者分别选用VOF多相流模型和标准k-ε、Realizable k-ε等湍流模型对钢包底吹氩气过程、连铸过程、铜熔炼和吹炼过程等进行了模拟研究。
本文以某铜底吹炉为研究对象,基于冷态水模实验和热平衡理论计算得到蘑菇头尺寸,随后利用Fluent商业软件对实际热态铜底吹炉气体喷吹与气液两相流进行模拟仿真,研究了气泡形貌、气泡上升时间及蘑菇头的影响。
1 计算模型
1.1 几何模型
首先基于一定假设,根据热平衡理论计算得到蘑菇头的尺寸大小,如图1所示,假设条件如下:
(1) 蘑菇头为半球状,其直径为n倍的喷枪外径(n>1);
(2)高温熔体与蘑菇头之间的传热以对流换热为主;
(3)蘑菇头得到的热量来自于高温熔体,失去的热量为喷枪喷吹的冷气体经过蘑菇头带走的热量。
计算得n=2.86。
另外通过水模实验研究[10],得到蘑菇头尺寸约为喷枪外径的的2.75倍(见图1)。
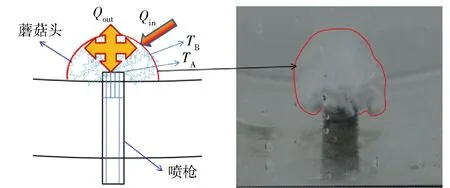
图1 蘑菇头尺寸确定
本文在模拟研究中假设铜底吹炉氧枪出口端已生成稳定蘑菇头,综合热平衡计算和水模实验结果,计算中将蘑菇头区域设置为半球形多孔介质区域,直径为喷枪外径的2.8倍。
铜底吹炉结构庞大,本文主要研究单枪0°倾角情况下蘑菇头对炉内流动的影响作用,为便于建模和减少计算时间,截取底吹炉某一切片的2/3部分建模并划分网格。简化后几何计算几何模型如图2所示,模型与原型比例1∶1,半径为3.88 m,炉体长度1.25 m,氧枪直径32 mm,凸起高度100 mm。
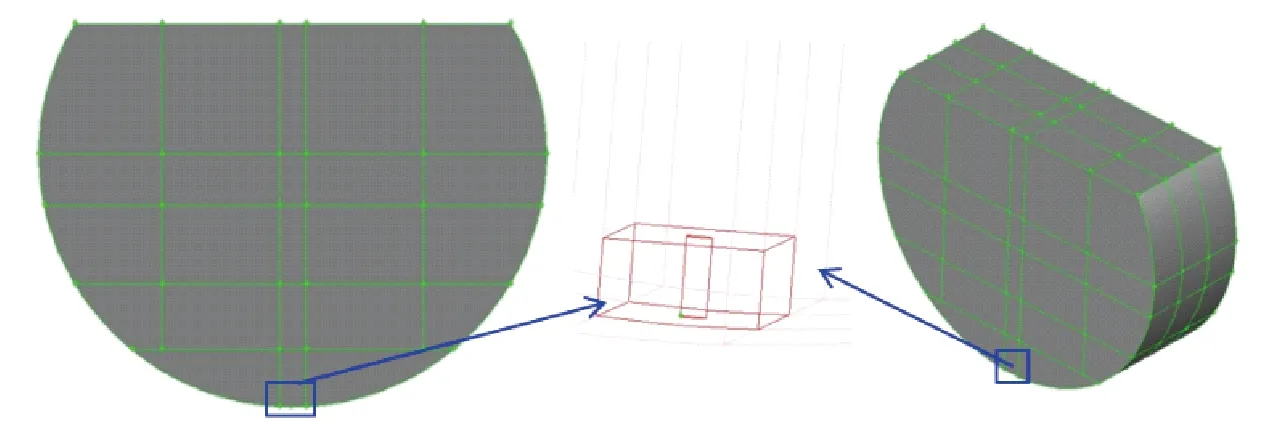
图2 计算几何模型
几何模型并不规则,为生成较高质量的网格,采用分块划分和局部加密方法进行网格划分,有蘑菇头和无蘑菇头时模型网格数分别为57.4万和58.1万,不存在负网格,网格质量良好。网格划分的情况如图3所示。
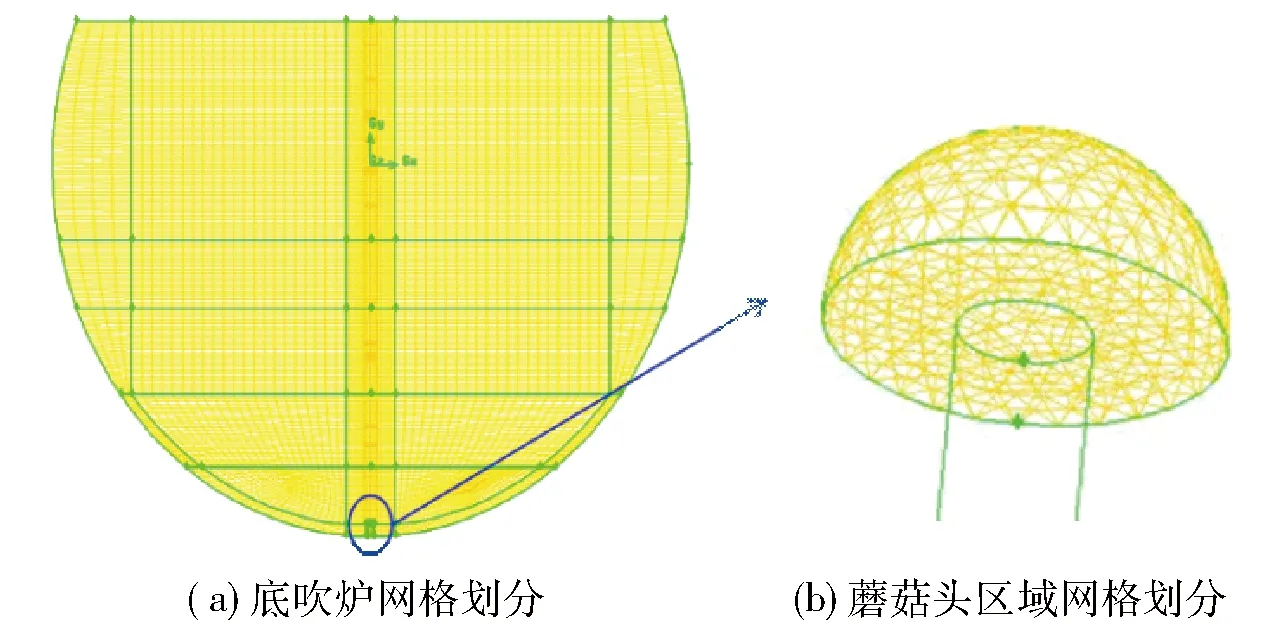
图3 网格划分
1.2 模型假设
为便于模拟计算,本文计算模型提出如下假设:
(1)熔池内液相全部为铜锍,气相为空气,忽略渣层;
(2)忽略炉内化学反应和温度场变化,忽略温度对气相影响;
(3)气相为理想流体,液相为不可压缩流体,密度、粘度等物性参数不随时间变化;
(4)假设初始状态熔体静止,忽略喷溅熔体损失;
(5)炉衬为绝热体,壁厚对模拟结果影响不大。
1.3 数学模型
选取VOF两相流模型模拟炉内气液两相流动,VOF模型基本控制方程如下:
1.3.1 体积分数方程
对气液两相流,VOF模型中提出了体积函数α概念,α的值定义为单元中流体所占体积与单元体积之比,通过建立和求解体积分数的连续性方程确定自由表面的位置,跟踪相与相之间的界面。当α=1,则单元体积内充满液体;当α=0,则单元体积内无液体;α=0~1时,单元体积中既有气体组分又有气体组分,此单元为自由表面单元,包含两相交界面。
(1)


Saq——源项,默认为0;
Vq——为第q相的速度,m/s;
ρq——为第q相的密度,kg/m3;
αq——为第q相的体积分数。
1.3.2 动量方程
在整个计算区域内,求解单一动量方程,计算得到的速度场结果由各相共享,动量方程如下所示:
(2)
式中:F——作用于控制容积上的体积力,N;
g——重力加速度,m/s2;
μ——为有效粘度,Pa·s;
V——流体速度,m/s;
p——压力,Pa。
湍流模型,本文采用标准的k-ε模型来描述湍流。湍动能k方程和耗散率ε方程如式(3)和式(4)所示:
(3)
(4)
式中:Gk——由于浮力引起的湍动能k的发生项,kg/(m·s3);
Gb——平均速度梯度引起的湍动能k的发生项,kg/(m·s3);
YM——可压缩湍流中脉动扩张项,kg/(m·s3);
σk、σε——湍动能k和耗散率g所对应湍流普朗特数;
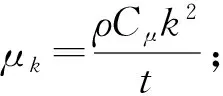
C1ε、C2ε和C3ε——湍流经验常数;
Sk——用户自定义湍动能源项,kg/(m·s3);
Sε——用户自定义湍流耗散率源项,kg/(m·s4)。
关于模型常数设置如表1所示。

表1 模型参数设置
1.4 多孔介质模型
多孔介质模型其实是指在定义为多孔介质的区域增加了主要根据经验假设和经验常数的流动阻力。从本质上来说,多孔介质模型仅仅是在动量方程上增加代表动量消耗的动量源项,此源项主要由粘性损失项和惯性损失项组成,用于模拟多孔介质对流动的影响作用。Fluent中多孔介质模型除多孔介质区域大小和孔隙率之外,还需参考经验数据设置粘性阻力和内部阻力系数。
2 边界条件及求解策略
2.1 边界条件与初始条件
(1)模型入口条件为速度入口,气流速度为133.92 m/s,湍流强度3.08%,喷枪当量直径32 mm,出口条件定义为压力出口,出口压力设置为0 Pa;
(2)壁面边界条件采用无滑移边界条件,近壁区域则采用标准壁面函数进行处理;
(3)模型下部为铜锍熔体区域,上部为空气区域,空气与铜锍间的表面张力为0.33 N/m;
(4)蘑菇头区域设置为多孔介质区域,孔隙率为0.2;
(5)操作压力设置为101 325 Pa,重力加速度设置为9.8 m/s2;
(6)液态铜锍熔体温度为1 473 K,初始熔体深度为1 545 mm。
2.2 求解策略
为了保证计算准确性,采用双精度模型进行变时间步长非稳态计算,Courant数为2,最小时间步长限制为10-5s。压力- 速度耦合方式采用压力耦合方程组半隐式SIMPLE法;梯度插值选用Least Squares Cell Based method;压力离散选用PRESTO;采用二阶迎风格式来离散动量方程;体积率方程采用Geo-Reconstruct格式;湍动能和耗散率输运方程的离散采用一阶迎风格式;控制方程残差为10-3。
3 结果与讨论
3.1 模型验证
首先将不存在蘑菇头情况下,底吹气流刚开始喷吹时气泡形貌变化情况模拟结果与实验结果进行对比,以验证数学模型的正确性。如图4a、4b、4c和4d所示,从第一个气泡生成到第一个气泡脱离,再到第二个气泡生成,以至多个气泡融合的过程中,可以看出气泡的形貌变化。随着气体的不断喷入,气泡逐渐长大,到一定时间之后,第一个气泡会与喷枪出口截面发生脱离,喷吹过程中气体在与液体的表面张力作用下变形、破碎,最终从液面溢出。从图4中可以看出,射流初期气泡形貌的模拟结果与水模实验非常接近,数值模拟与水模实验所得到的气泡运动过程的结果是基本一致的,利用本文所建立的数学模型对铜底吹炉内的气液两相流动过程进行模拟是可行的,得到的模拟结果准确性较高。
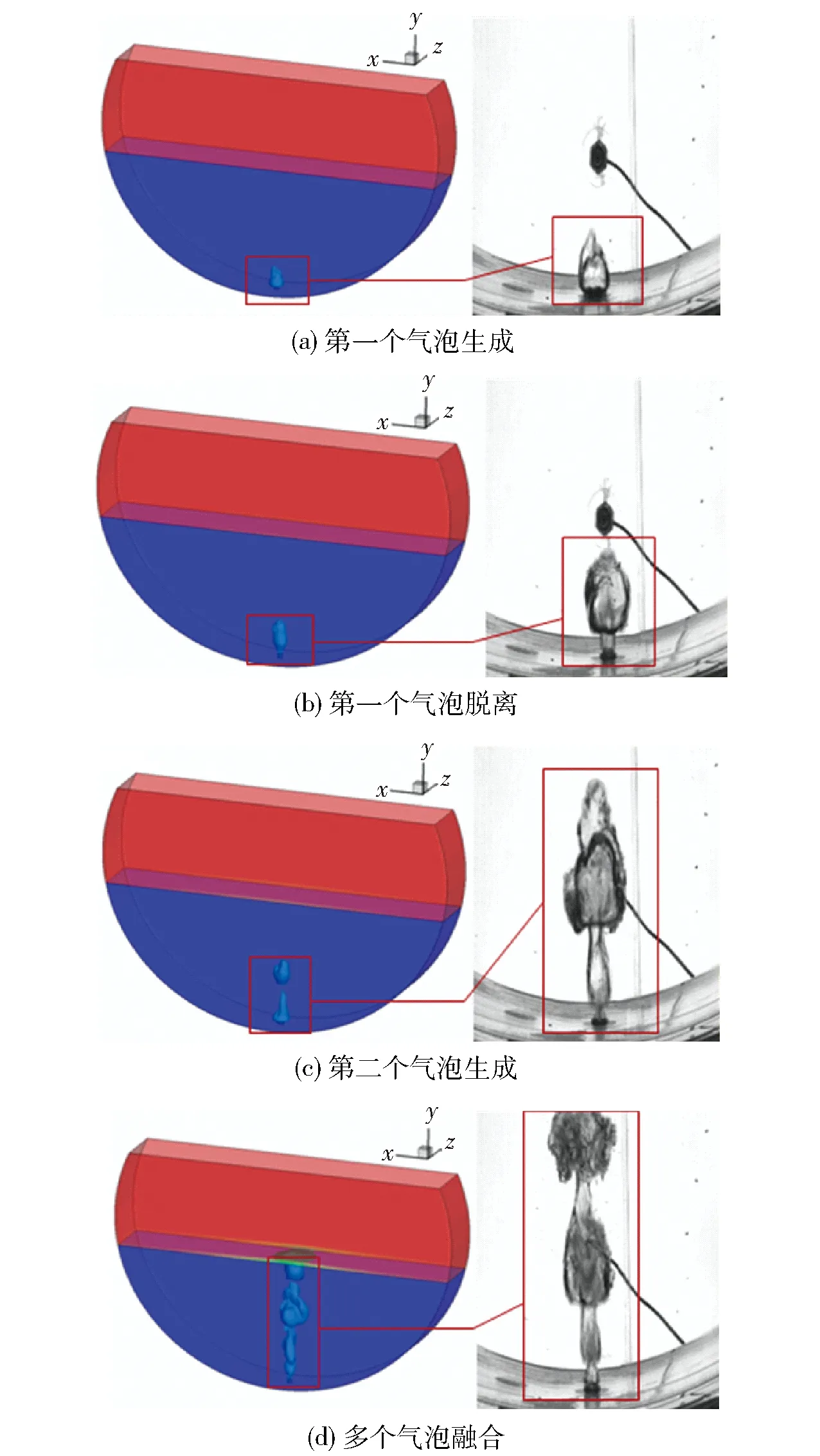
图4 无蘑菇头时模拟与实验结果气泡形貌对比
3.2 气泡上升过程形貌变化
针对存在蘑菇头和不存在蘑菇头两种情况,分别建立数学模型并模拟得到底吹气流喷吹时气泡上升过程形貌变化。存在蘑菇头时,气泡上升过程形貌变化如图5a所示。底吹气体从氧枪喷出后,首先在喷口处形成近似小球状气泡,第一个气泡体积不断膨胀变大,大约经过0.2 s明显横向膨胀后开始竖直抬升;在第一个气泡上升过程中,随着底吹气体持续喷吹,第二个气泡开始生成、长大并与第一个气泡分离;随后第三个气泡开始生成、长大并与第二个气泡分离,不断重复这一过程。在第一个气泡产生之后,气泡生成频率变快,且每个气泡都存在生成、分离、长大的过程。在气泡上升过程中,由于底吹氧枪不断喷入高速气流,新生成的气泡上升速度较快,而较早前生成气泡上升速度较慢,新生成气泡很快追上较早前气泡,部分融合形成更大蘑菇头状气泡。由于蘑菇头状气泡与熔池接触表面积增加,熔体液面对气泡上升过程的阻力变大,气泡上升速度减慢,持续喷吹的底吹高速气流很快与其融合,形成新的蘑菇头状气泡,气泡继续浮升并冲破熔池表面发生液面波动现象,同时气泡破裂。不存在蘑菇头时,气泡上升过程形貌变化如图5b所示,与存在蘑菇头时气泡形貌变化相似,存在气泡的生成、长大和分离过程,不同之处如下:①由于不存在蘑菇头,第一个气泡生成阻力与存在蘑菇头时相比较小,第一个气泡不存在明显横向膨胀过程;②气泡生成频率较快;③气泡体积小于存在蘑菇头时的气泡体积。
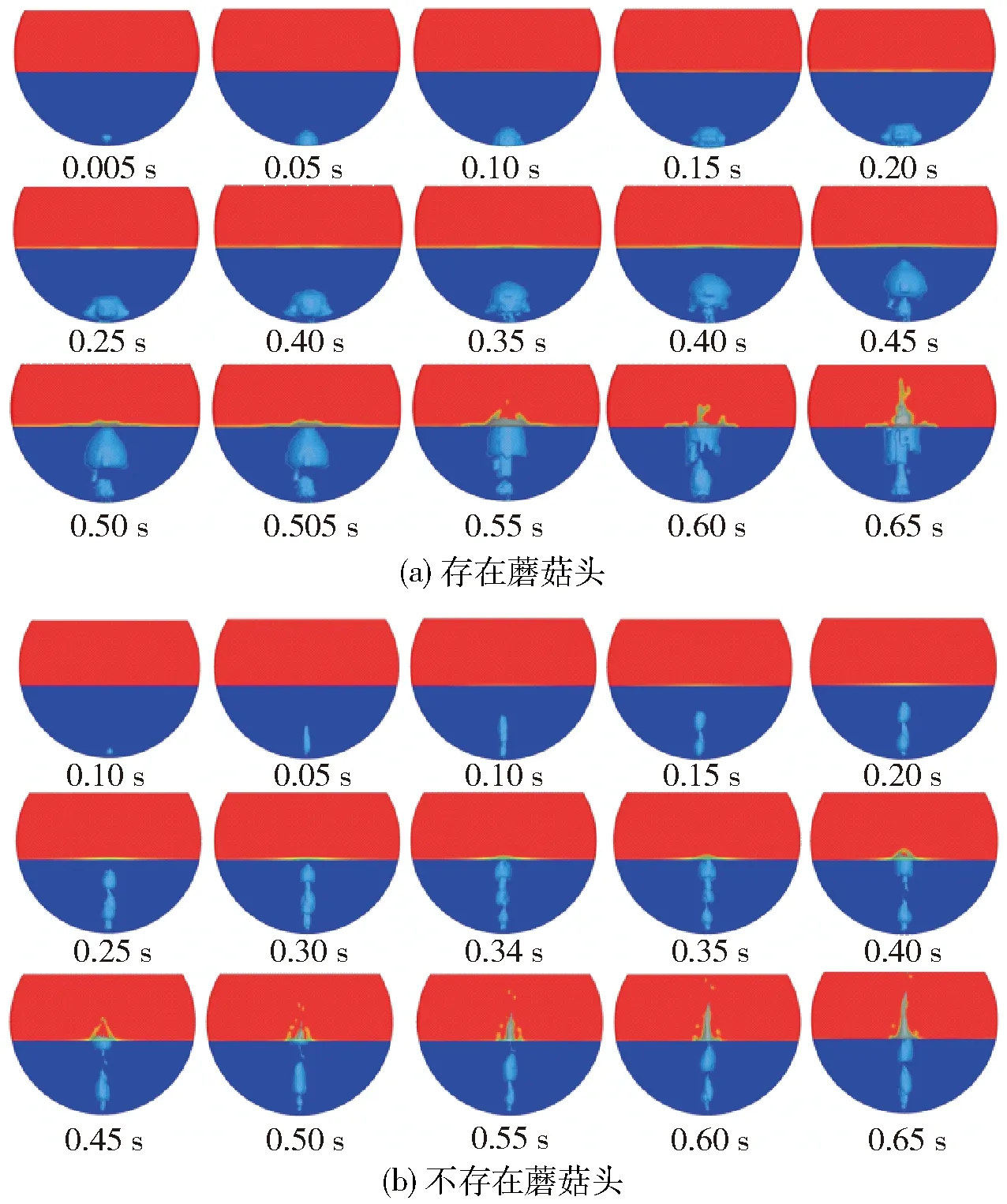
图5 底吹炉0.65 s时间内气泡上升过程形貌变化
3.3 蘑菇头的存在对炉内气液流动的影响
由图6可以看出,存在蘑菇头时气泡的体积明显大于不存在蘑菇头时气泡的体积。蘑菇头的存在使气体喷出速度方向不再只是竖直向上方向,也会向四周散开喷出,这造成气泡在横向方向膨胀明显,气流形状如图6b所示,而不存在蘑菇头时气泡无明显的横向膨胀,整体而看,气流形状会更像是柱状气流,如图6a。因此,在不堵塞底吹气流不断喷入前提下,底吹炉氧枪出口端蘑菇头的存在一定程度上可以使气泡与熔体间接触更充分。
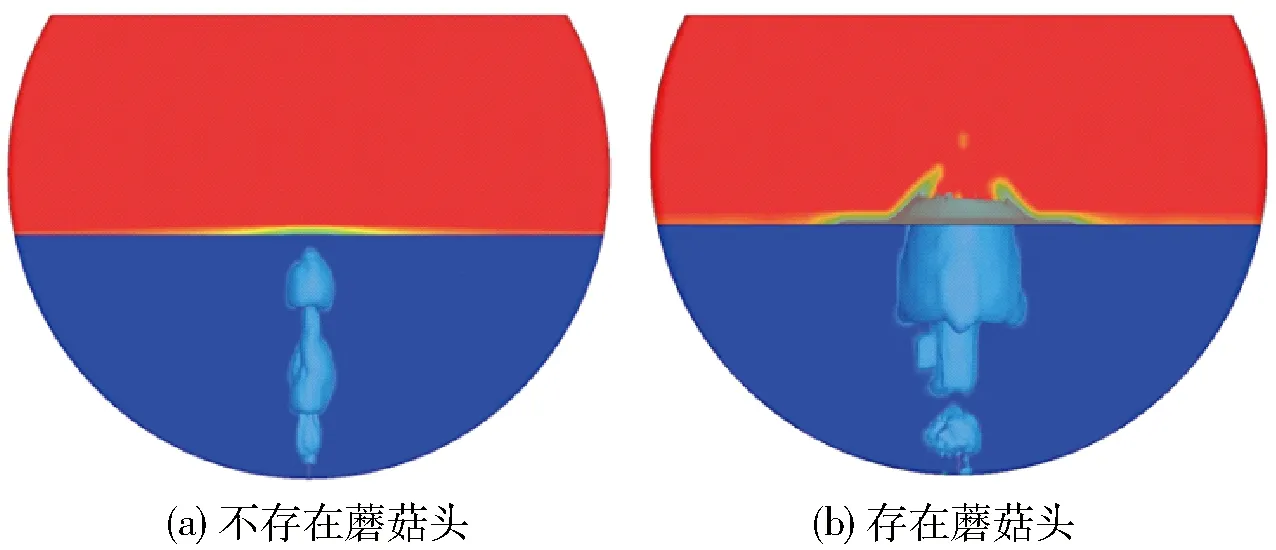
图6 存在和不存在蘑菇头时底吹气流对比
气泡簇到达液面的时间可以反映出气泡在炉内的停留时间长短,由图5a可知存在蘑菇头情况下气泡簇到达液面时间为0.505 s,图5b显示不存在蘑菇头时气泡簇到达液面时间为0.34 s。对比发现,存在蘑菇头情况下,气泡到达液面的时间比不存在蘑菇头时的时间要长,大约为其1.49倍。因此蘑菇头的存在一般可以使气体在炉内停留更长的时间,这有利于炉内反应充分进行。
综上所述,蘑菇头的存在对炉内流动的影响主要体现在气泡形貌和气泡到达液面时间等方面,蘑菇头存在时,气泡的体积会更大且横向膨胀明显,到达液面的时间会更长即在炉内停留时间变长,这在一定程度上有利于炉内熔体与底吹气体之间进行更充分的反应。
4 结论
(1) 基于通过热平衡理论计算得到半球状蘑菇头区域直径为喷枪外径的2.86倍,水模实验结果得到蘑菇头直径为喷枪外径的2.75倍,误差3.85%;水模实验模拟得到蘑菇头基本为半球状多孔介质区,数值模拟计算将蘑菇头区域假设为半球形符合实际。
(2) 模拟研究了存在蘑菇头时底吹气流喷吹过程气泡形貌变化。气体从氧枪喷出后形成蘑菇状气泡,随后断裂为两部分,上半部分与球状气泡融合,下半部分则与新气泡结合。新气泡流速较大,很快与之前气泡融合为新蘑菇状气泡,过程不断重复。第一个气泡生成、膨胀和分离耗时较长,随后气泡生成频率加快,每个气泡都存在生成、长大和分离过程。
(3) 蘑菇头的存在会影响炉内流动,蘑菇头存在时气泡体积更大,气泡横向膨胀明显;气泡到达液面的时间会更长,约为不存在蘑菇头时气泡到达液面时间的1.49倍。合理控制蘑菇头,可以使底吹气体与熔体接触面积增加,气体在炉内停留时间更长,这都有利于炉内反应充分进行。
目前关于底吹炉蘑菇头方面的研究较少且不成熟,本文中模型的建立也是建立在相当多的假设上的,未来会对其进行更为细致的研究。
[参考文献]
[1] 蒋继穆.氧气底吹炉连续炼铜新工艺及装置简介[A]. 中国首届熔池熔炼技术及装备专题研讨会论文集[C], 2007.
[2] 陈知若.底吹熔池炼铜技术的应用[J]. 中国有色冶金, 2009 (5): 16-22.
[3] 张晓兵,曹兆民,李洪利.顶底复吹转炉底吹喷嘴端部蘑菇体的冷模拟研究[J].钢铁,1992(8):22-25.
[4] 袁集华,陈永定,唐仲和等. 底吹喷枪出口端蘑菇头形成机理及模拟研究[J]. 钢铁研究学报,1994(1):5-8.
[5] 刘浏,佟溥翘,崔淑贤等.长寿复吹转炉工艺技术开发[J].钢铁,2002 (10):13-15.
[6] 陈树林,陈红伟,张太生.复吹转炉底吹“蘑菇头”的形成及维护实践[J].钢铁研究,2010(z2):103-105.
[7] LI Bao-kuan,YIN Hong-bin, ZHOU Qian,et al. Modeling of three-phase flows and behavior of slag/steel interface in an argon gas stirred ladle[J]. ISIJ International, 2008(12): 1704-1711.
[8] Yu Hai-Qi, Zhu Miao-Yong, Wang Jun,et al. Interfacial fluctuation behavior of steel/slag in medium-thin slab continuous casting mold with argon gas injection[J]. ISIJ International. 2010 (4): 5-11.
[9] 闫红杰, 刘方侃, 张振扬等. 氧枪布置方式对底吹熔池熔炼过程的影响[J]. 中国有色金属学报, 2012(8): 2393-2400.
[10] 王书晓,余跃,温治等.铜底吹炉氧枪出口端蘑菇头生成过程水模实验研究[J].中国有色冶金,2018(1):47-53.

