高层钢结构住宅结构性能研究

朱 华 （安徽省建筑科学研究设计院，安徽 合肥 230001）

1 工程慨况

1.1 工程简介

本工程为一拟建于合肥市的高层钢结构住宅，结构型式为钢框架-支撑结构体系，建筑户型为2梯4户，对称分布，如图1所示。结构高度为81m，共27层，每层建筑面积为638.5m2，建筑总面积为17239.5m2。

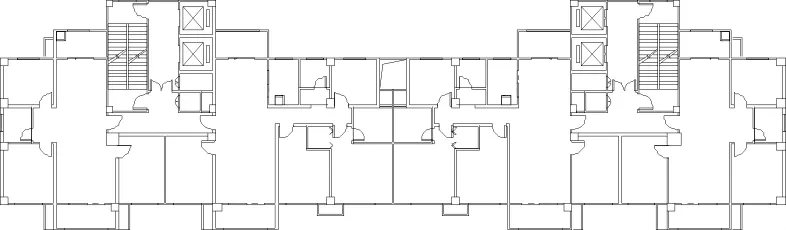
图1 标准层平面图

1.2 设计参数及荷载取值

本工程为丙类建筑，设计使用年限为50年，各设计参数及荷载取值见表1和表2所示。

设计参数 表1

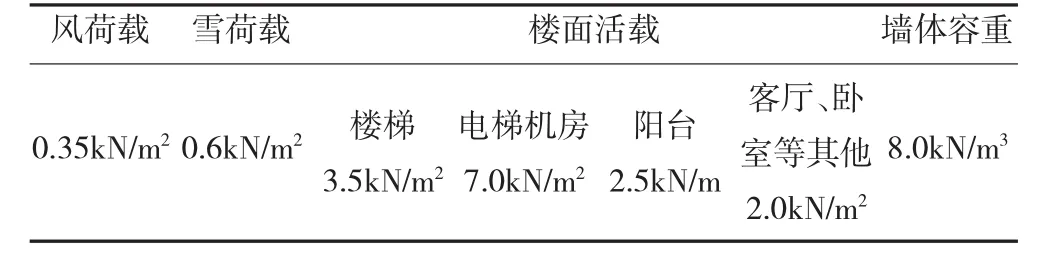
荷载取值 表2

2 两种结构体系对比分析

2.1 结构布置

本工程分别采用方矩钢管混凝土柱结构体系和方矩钢管柱结构体系进行布置。方矩钢管混凝土柱结构体系即在钢柱中填充自密实混凝土，而方矩钢管柱结构体系中的钢柱则无混凝土填充。本工程对方矩钢管混凝土柱结构体系与方矩钢管柱结构体系采用相同的结构布置，如图 2（a）、图 2（b）所示。两种结构所用钢材均选用Q345B型号，螺栓采用10.9级摩擦型高强螺栓。经试算后，两种结构体系的柱截面尺寸如表3所示。

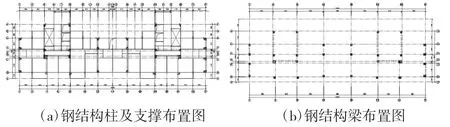
图2 结构布置图

2.2 结构分析

对两种结构体系采用SATWE程序进行结构分析，由分析结果可知，两种结构体系的主要技术指标对比如表4所示。这两种结构体系的计算结果均满足我国现行规范及规程的要求。由表中数据我们可以知道，方矩钢管混凝土柱结构体系和方矩钢管柱结构体系各项技术指标中主要的不同之处为最大层间位移角，方矩钢管混凝土柱结构体系的层间位移角明显要小很多。由此我们可以得出，在钢柱中灌注混凝土后使结构的整体刚度变大了。

2.3 材料用量比较

根据PKPM软件中对结构材料的统计，可以得到方矩钢管混凝土柱结构体系的总用钢量为1330.2t，折合成每平方米用钢量为77.2kg/m2，方矩钢管柱结构体系的总用钢量为1487.2t，合86.3kg/m2。而方矩钢管混凝土柱结构体系中钢管柱内所灌筑的混凝土总量约为460m3，合每平方米增加混凝土用量为0.0267m3。可以看出，方矩钢管混凝土柱结构体系相比于方矩钢管柱结构体系而言，混凝土用量每平米增加0.0267m3，钢材用量每平米可减少9.1kg，柱用钢量可减少35%左右。

主要柱截面尺寸(单位：mm) 表3

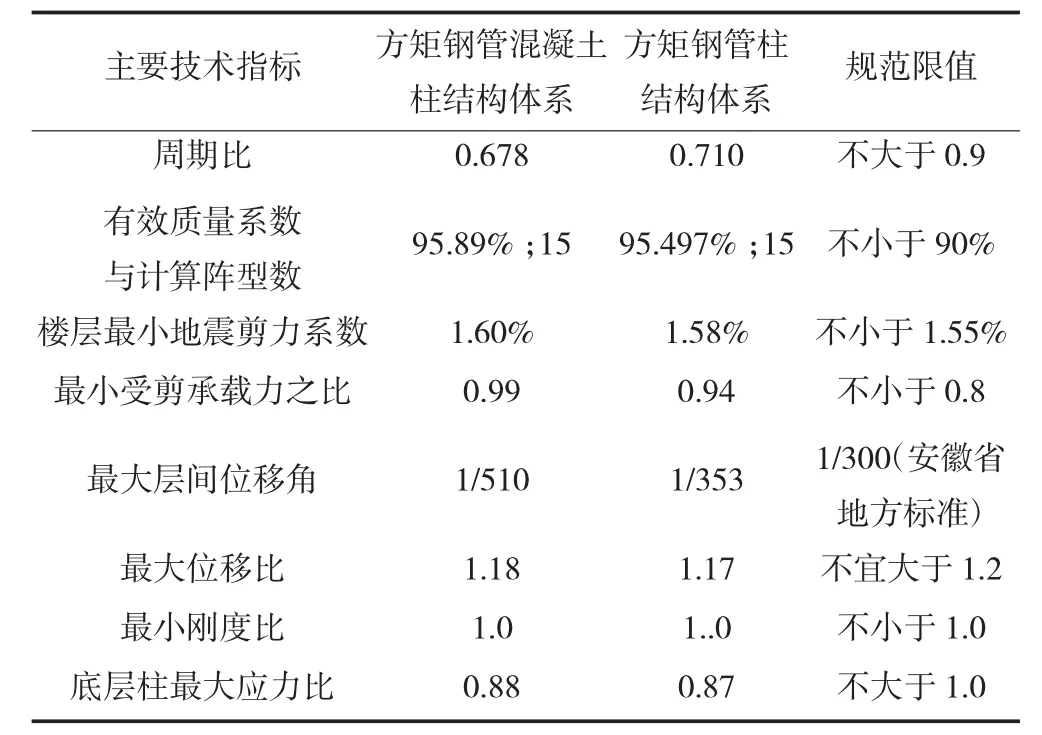
结构性能指标对比 表4

3 结构性能分析

3.1 性能目标选取

采用静力弹塑性法和动力非线性时程分析法对所建立的两种结构模型进行结构性能的分析。由《建筑抗震设计规范》（GB50011-2010）（以下简称《抗规》）附录M中表M.1.1-2所推荐的性能目标与层间位移角的关系，选取性能目标3做为结构的性能目标。罕遇地震作用时，性能目标与层间位移角限值的对应关系如表5所示。

性能目标与层间位移角限值的对应关系 表5

3.2 静力弹塑性分析

3.2.1 静力弹塑性分析方法

静力弹塑性（Pushover）分析的核心问题是找到结构的性能点，其方法一般可按某种规律对结构施加侧向位或移侧向力，直至结构模型的最大平动位移或控制点位移达到设定的破坏位移为止（其中破坏位移一般可取结构高度的1/100或2/100），从而得到结构在侧向荷载作用下的荷载-位移曲线图，再进一步将荷载-位移曲线图转化为加速度-位移曲线图，即结构的能力谱曲线图。然后根据条件建立目标地震作用下的需求谱曲线，将能力谱曲线和需求谱曲线画在同一坐标系中，从而求得结构的性能点。

3.2.2 静力弹塑性分析结果

本工程将对方矩钢管混凝土柱结构体系和方矩钢管柱结构体系所建立的两种模型分别用Midas Gen软件进行Pushover分析。其中柱铰布置轴力-弯矩铰（P-M-M型铰）、梁铰布置弯矩铰（My铰）、支撑布置轴力铰（Fx铰），塑性铰曲线采用FEMA骨架曲线。分别从X、Y两个方向采用振型法进行加载。设定7度（0.1g），第1地震分组，Ⅱ类场地，罕遇地震影响的需求谱，得到两种结构体系下模型的性能点，如表6所示。两种模型在结构性能点处的最大层间位移角如表7所示。

两种结构体系下模型的性能点对比 表6

由表7可知，两种结构模型在X向加载工况下的层间位移角均比Y向加载工况下的层间位移角大。由最大层间位移角结果可知，两种不同结构体系下结构的性能均能达到性能目标3的要求。且方矩钢管柱结构体系模型已达到性能目标2的层间位移角要求。由此可见，钢混凝土柱结构体系模型与钢柱结构体系模型相比，后者的抗震性能相对较好。

两种结构体系下模型的性能点处结构最大层间位移角对比 表7

以X向加载工况为例，两种结构模型在性能点处塑性铰的发展情况如图3和图4所示。由图3、图4可知，在罕遇地震作用下，结构塑性铰均先出在梁和支撑上，柱均无塑性铰的出现。同时从结构性能点处塑性铰的布置情况看出，方矩钢管柱结构体系模型相对于方矩钢管-混凝土柱结构体系模型而言，具有更大的安全储备。

图3 罕遇地震下方矩钢管-混凝土柱结构体系模型性能点处塑性铰状况

图4 罕遇地震下方矩钢管柱结构体系模型性能点处塑性铰状况

3.3 动力非线性时程分析

3.3.1 动力非线性时程分析参数

PUSHOVER分析还仅是一种拟动力分析，还不能完全反映结构在实际地震波作用下的抗震性能。采用Midas-Gen软件对两种结构模型进行罕遇地震作用下的弹塑性时程分析，根据规范要求，选取了两条实际强震波和一条人工波对两种结构模型进行弹塑性时程分析。两条实际强震波分别为1940年记录的El Centro波和1952年记录的Taft波。根据《抗震规》中表5.1.2-2规定，将3条地震波的加速度峰值均调整到7度（0.1g）罕遇地震作用下的220cm/s2，分别从X向和Y向对结构加载进行动力时程分析。其中，柱定义轴力-弯矩铰（Fz轴力铰和My、Mz弯矩铰），采用随机硬化的滞回曲线模型；梁定义弯矩铰（My方向），采用双折线的滞回曲线模型；支撑定义轴力铰（Fz方向），采用双折线的滞回曲线模型，动力分析方法选择直接积分法，以0.02s为时间步长进行分析。

3.3.2 动力非线性时程分析结果

两种结构模型在3条地震波作用下的最大层间位移角如表8所示。由表8可知，两种结构模型均满足性能3的层间位移角限值规定，且接近性能目标2的层间位移角限值规定，方矩钢管混凝土柱结构体系模型的层间位移角均比方矩钢管柱结构体系模型的层间位移角略小。

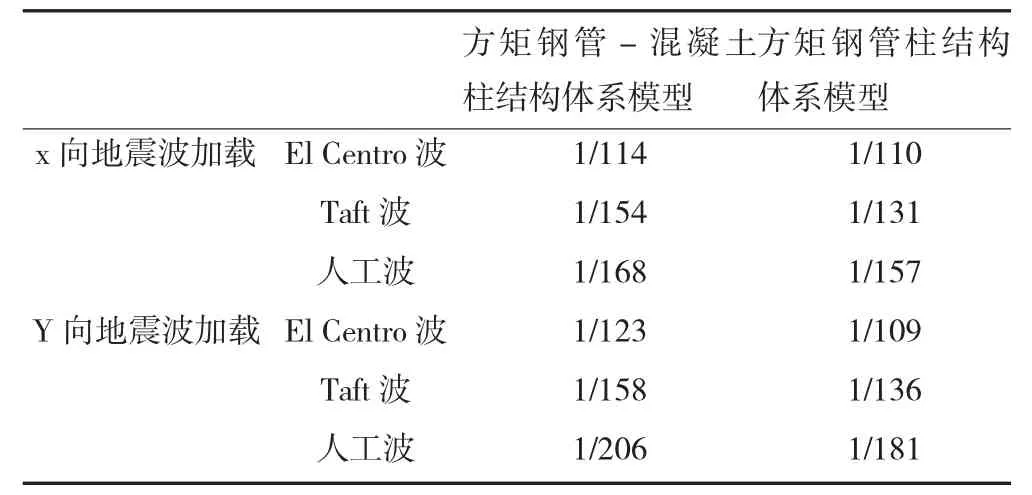
两种结构体系下模型的最大层间位移角对比 表8

X向地震波加载下两种结构体系非弹性铰延性分布情况 表9

以X向地震波加载为例，列出两种结构模型在3条地震波加载过程中，结构非弹性铰铰的延性分布情况如表9所示。图中Lever-1表示铰还处于弹性阶段，Lever-2表示铰已达到屈服状态，Lever-3、Lever-4、Lever-5表示各构件的延性依次递增。在分析结果中对于上述5个状态分别以蓝色、深绿色、浅绿色、橙色和红色来表示。由分析结果可知，两种结构模型在3条地震波作用下，结构中有部分梁和支撑的非弹性铰铰进入塑性阶段（Lerer-2阶段），柱铰均在弹性阶段。在各条地震波作用下，两种结构体系下模型中铰的分布情况相似，也即说明两种结构具有相近的抗震性能。

4 结论

本文对同一高层钢结构住宅建筑采用了两种结构模型进行了对比分析，从而得出了如下结论：

①高层钢结构住宅，在柱中灌筑混凝土可减少柱用钢量35%左右，而混凝土用量每平方米仅增加0.03m3左右，具有一定经济性；

②在方矩钢管柱中灌注混凝土可提高结构整体的抗侧刚度，减小水平作用下结构的层间位移角；

③由于在柱中灌注混凝土而减少柱用钢量，在罕遇地震作用下，方矩钢管混凝土柱结构模型的整体延性略小于方矩钢管柱结构模型。柱中灌注混凝土后，在罕遇地震作用下结构的抗震性能略为下降。

[1]李国强.多高层建筑钢结构设计[M].北京:中国建筑工业出版社，2004:10-23.

[2]JGJ99-2015，高层民用建筑钢结构技术规程[S].

[3]GB50017-2003，钢结构设计规范[S].

[4]GB50011-2010，建筑抗震设计规范[S].

[5]王迎春，朱华.方矩管混凝土柱高层钢结构住宅结构性能分析[J].安徽建筑，2017，24(05).

[6]沈康.小截面柱高层钢结构住宅性能分析[D].2015.