基于虚拟样机的3缸机曲轴系扭振分析及优化研究
董俊红,李伟,杨征睿,刘佳鑫,聂尔冰
(1.中国汽车技术研究中心,天津 300300;2. 吉林大学,吉林 长春 130022;3.中国民航大学,天津 300162)
随着国内汽车市场竞争的日益激烈,汽车的驾驶平顺性、振动及噪声逐渐成为影响产品销量的重要指标,发动机NVH性能也越来越受到主机厂的关注[1]。小型3缸汽油机作为混合动力的主力机型,在当前节能减排的大环境下,引起了国内外厂家的高度重视和大力开发。而曲轴扭振问题是发动机研发过程中必须重视的关键点之一,扭振发生时,曲轴系会产生交变扭转应力,导致传动机构磨损加剧,发动机功率下降,燃油经济性和可靠性变差,甚至曲轴断裂[2],极大影响发动机的NVH特性。对于扭振问题,应用虚拟样机技术可以节省计算时间和研发成本,避免无谓的摸索,可为发动机的设计提供巨大的便利。
国外对曲轴扭振的研究起步较早,取得了丰富有指导意义的成果。Maciej Zawisza针对橡胶减振皮带轮进行研究,发现改变橡胶环的参数会影响整个曲轴系的弹性[3]。C. Jagielowicz-Ryzna等通过大量的计算说明曲轴扭振谐振程度与强迫振动阶次的关系[4]。G.W. Kim等介绍了一种压电式能量回收装置PEH来回收曲轴扭转振动能量[5]。M. Dereszewski等尝试使用IAS(曲轴两端瞬时角速度)的方法来监测曲轴的扭振状况[6]。B. Chiliński, M. Zawisza等针对曲轴系和扭振减振器进行了详细的建模和计算分析[7]。B. Kareem通过模型分析了曲轴扭振、轴承润滑等其他因素对曲轴失效的贡献[8]。国内近些年在曲轴扭振方面的研究也发展迅速。李静、王东方等应用ADAMS软件以及对扭振振幅进行FFT操作,得出曲轴前端扭转变形的主因是该转速下的频率及谐次频率[9]。上官文斌、陈超等对曲轴系扭振以集总参数模型进行了理论计算,计算结果与试验值吻合较好[10]。
本研究基于一款缸内直喷3缸汽油机,采用有限元法及一维和三维多体动力学法,详细分析了发动机的扭转振动特性,并对比了一维模型和三维模型计算的精确度,且以虚拟样机技术为基础结合试验测试解析了该款发动机在NVH设计上的先进理念,为国内同类自主产品的开发设计与改进提供了重要的参考依据。
1 虚拟样机模型
1.1 发动机虚拟样机模型建立
将曲轴系和缸体视为柔性体[11],利用AVL EXCITE软件建立该3缸机虚拟样机模型(见图1)。为保证模型计算结果的准确性,虚拟样机的边界条件需尽量与实际情况一致,全部采用实测值。图2示出发动机实测缸内燃烧压力。其中,虚拟样机一维Designer模型相关参数设置由三维Power Unit模型简化而得到,以此实现一维和三维的精准建模。

图1 虚拟样机模型
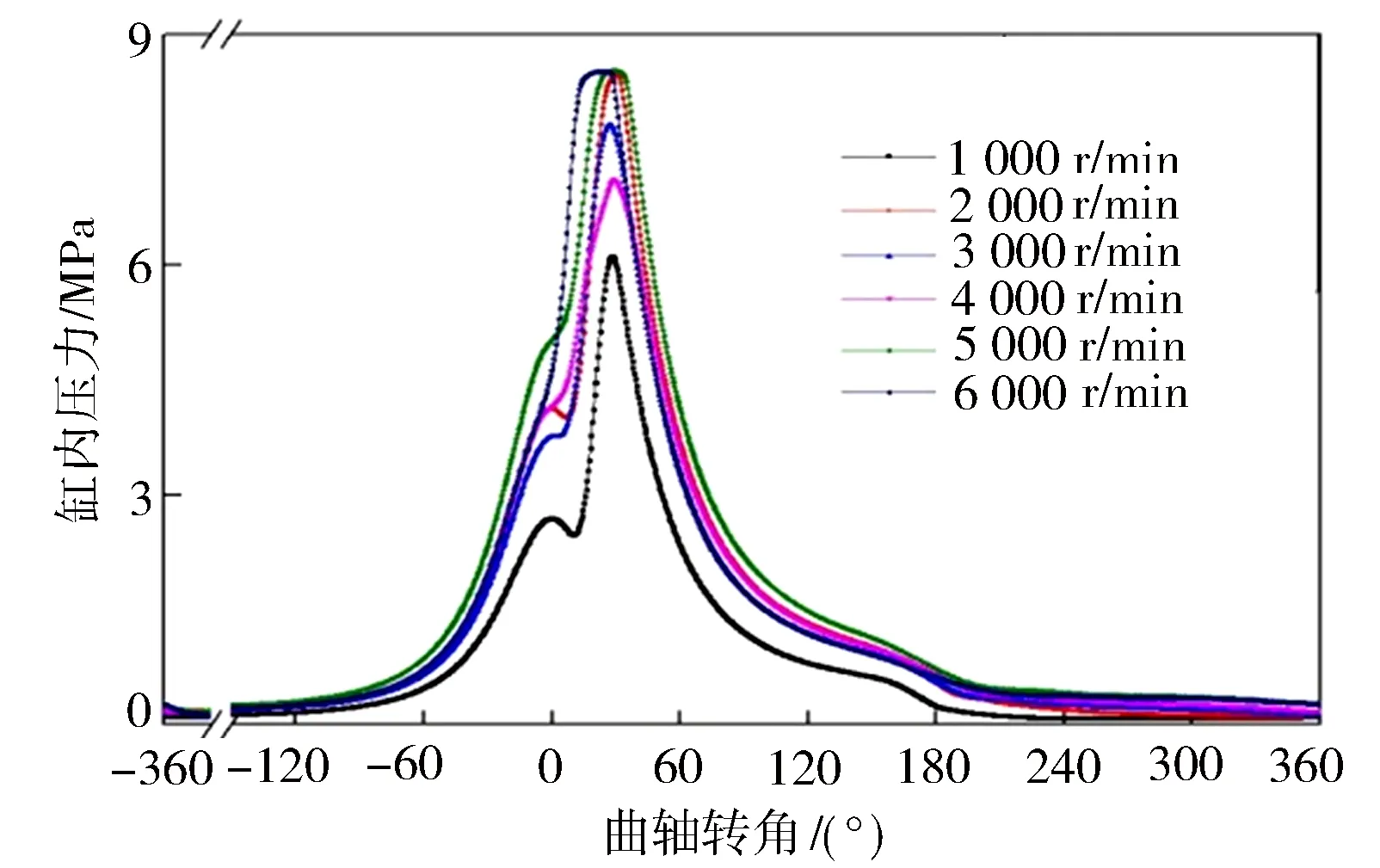
图2 缸内燃烧压力边界条件
1.2 模态综合法基本理论
建立曲轴柔性体有限元模型,采用二阶四面体对曲轴进行有限元建模,曲轴有限元模型见图3。
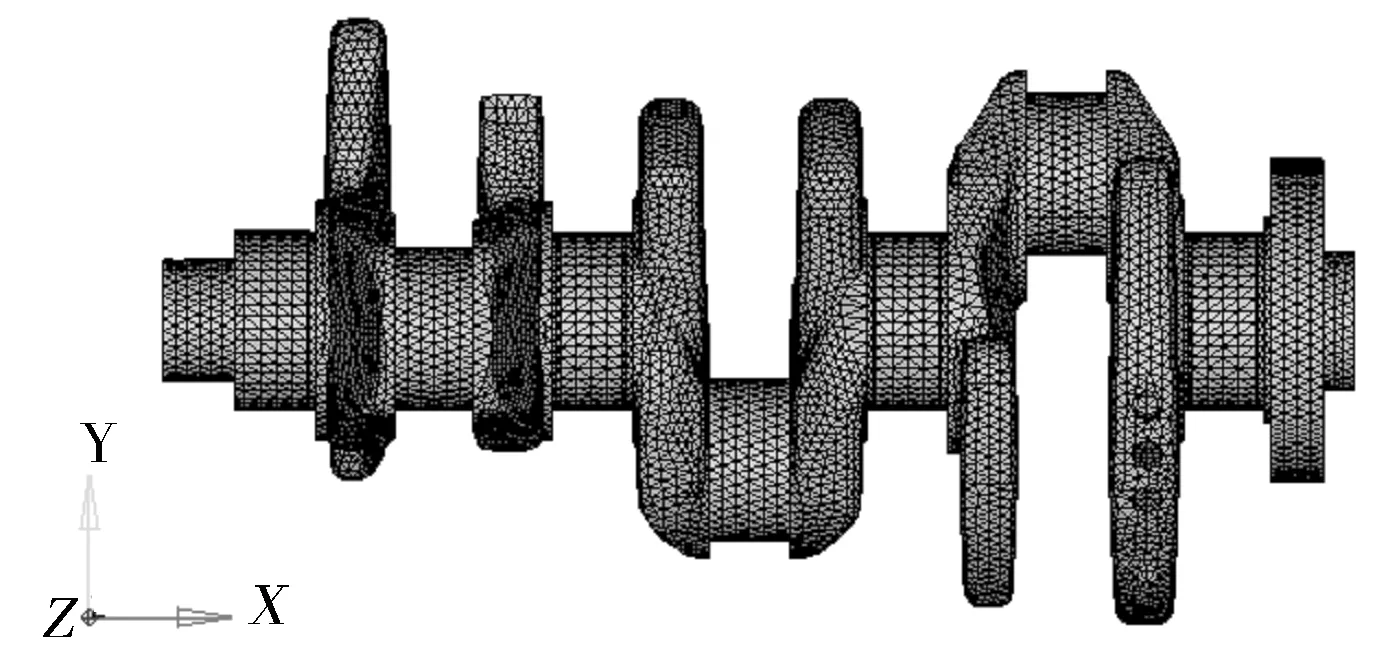
图3 曲轴系有限元模型
对于复杂大型结构件的有限元计算,通常采用模态综合法。模态综合法的基本思想是把复杂结构分成若干个子结构,然后用离散化方法对子结构作各种力学分析,得到各子结构的模态,再然后通过坐标变换,得到用独立的各子结构模态坐标组成的描述整个系统运动的独立广义坐标[12]。在Abaqus软件中进行曲轴系有限元模型的缩减工作,将缩减好的有限元模型利用AVL Excite软件中的Abaqus接口导入Excite虚拟样机模型中,该接口可实现两软件间的无缝连接。模态综合法能够大量减少计算模型的自由度,从而节约计算资源与计算时间。下面详细介绍模态综合法的基本过程。
首先,将子结构的位移分为界面位移矢量xj和内部位移矢量xz,子结构运动方程可描述为
(1)
式中:M为质量矩阵;K为刚度矩阵;F为结构受力。
然后,通过坐标变换将物理坐标X变换到模态坐标Y,坐标变换矩阵见式(2):
(2)
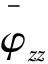

(3)

1.3 柔性体多体动力学方程
柔性体多体动力学是在刚体多体动力学上发展起来的。柔性体多体动力学理论进一步考虑了结构件弹性对计算结果的影响,相比刚性体多体动力学理论具有更高的准确性,是目前理论研究和应用力学领域使用最广泛的理论。基于拉格朗日的柔性体多体动力学方程表述为
(4)

1.4 多体动力学模型有限元验证
为保证计算模型能够模拟实际曲轴系工作状态,对有限元模型精度进行模态试验验证和标定。采用单点激励多点响应的方法,对每个测点的振动加速度信号,通过集总平均法得到模态频率。在模态试验时,为保证测量精度,曲轴模态测试采用弹性悬挂。同时,结构件模态频率测量时,各测点布置时尽量避开部件的模态节点。
曲轴模态频率的对比见表1,曲轴有限元模型的误差均保持在3%以内,远远小于一般工程计算5%的要求,保证了计算模型的精度。

表1 曲轴模态频率计算值与试验值对比
2 曲轴系扭振计算及试验
2.1 一维模型曲轴系扭振计算
2.1.1扭振频率与临界转速
一维扭振分析将整个曲轴系离散成当量惯量与当量扭转刚度构成的多质量点系统,分析模型在AVL EXCITE Designer中建立。曲轴系模型包括减振器总成(内圈Hub、外圈Ring及螺栓)、正时带轮、曲轴、飞轮及飞轮螺栓。
计算时需将活塞组件与连杆组件的惯量折算至对应的曲轴旋转中心线上。减振器减振性能的自身减振频率采用扭振试验数据反向标定法,结果为658 Hz,对应的扭转刚度为32 000 N·m/rad。离散后的当量曲轴系、当量惯量与当量扭转刚度见图4及表2和表3。
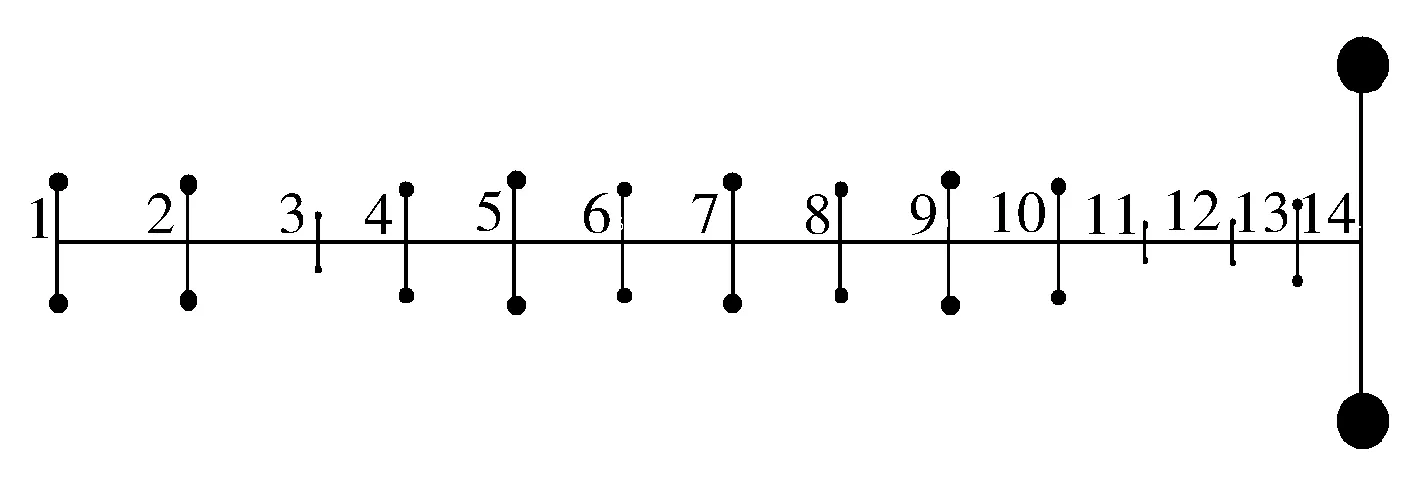
图4 当量曲轴系简化图

1DamperRing11.87e-032DamperHub1.24e-033Seg1⁃MainJournal11.32e-054MainJournal19.94e-045CrankPin12.71e-036MainJournal29.97e-047CrankPin21.89e-038MainJournal31.03e-039CrankPin32.86e-0310MainJournal41.11e-0311Segment1⁃MainJournal11.65e-0612Segment1⁃MainJournal15.75e-0613Segment1⁃MainJournal11.77e-0414Flywheel1.27e-01
表3曲轴轴段扭转刚度N·m·rad-1

1—2Damper3.200e+042—3Segment11.097e+053—4Half⁃MainJournal12.620e+054—5Web13.815e+055—6Web23.614e+056—7Web34.423e+057—8Web44.423e+058—9Web54.041e+059—10Web64.144e+0510—11Half⁃MainJournal42.897e+0611—12Segment21.425e+0712—13Segment32.171e+0713—14Segment42.128e+07
基于上述的当量惯量与当量扭转刚度,计算得到如图5所示的曲轴系扭振频率及振型图,前两阶扭振频率分别为419.4 Hz与759.7 Hz。从振型图中可知,对于重点分析的第一阶振型,越靠近自由端,相对振幅越大。扭振节点位于靠近飞轮的主轴颈附近。

图5 曲轴系扭振频率及振型图
进一步结合图6曲轴扭振临界转速图可知,在发动机工作转速范围1 000~6 000 r/min内,3缸机的主阶次1.5,3阶阶次线与频率红线无相交,即不会出现扭转共振,因此只需重点关注相交的4.5,6,7.5及9阶等阶次激励引起的扭转共振。

图6 曲轴扭振临界转速
2.1.2曲轴自由端扭转角及转速均匀度
对于曲轴系扭振,通常重点关注前端减振器的扭转角及后端功率输出端飞轮的转速均匀度。图7示出减振器Hub扭转角的阶次结果。对于4.5,6,7.5及9阶在不同转速引起的扭转共振,共振阶次、对应临界转速与扭振角分别为4.5阶/5 550 r·min-1/0.138°,6阶/4 350 r·min-1/0.054°,7.5阶/3 350 r·min-1/0.038°,9阶/3 000 r·min-1/0.024°,对应的扭振频率均为420 Hz左右,与自由模态分析吻合。1.5与3阶在低转速时的扭转角并非由扭转共振引起,而是由转速波动引起的(转速越低,波动越大)。

图7 减振器Hub扭转角
图8示出减振器Ring和飞轮转速均匀度(转速波动量与名义转速之比)结果,转速均匀度反映曲轴功率输出的均匀程度,波动量越小,发动机运转越平稳。两条曲线的总体趋势是随着转速增加,输出趋向平稳,飞轮端更加明显,是因其受扭振影响较小(飞轮相对扭振振幅较小)。减振器Ring受扭振影响相对较大,均匀度在3 000 r/min以上时并未单调降低,而是维持在7%~8%。

图8 减振器Ring与飞轮转速均匀度
2.2 三维模型曲轴系扭振计算
在EXCITE Power Unit计算中,通过有限元网格模型得到的曲轴系前两阶扭转固有频率分别为441.1 Hz和766.9 Hz,其中一阶扭转模态见图9。
图9 曲轴系一阶扭转模态
进行曲轴系扭振计算时,采用曲轴转速范围为1 000~6 000r/min、间隔100 r/min的稳态转速进行计算。图10示出减振器Hub在不同转速下的幅频特性Colormap图。图11示出减振器Hub扭转角的阶次结果。

图10 减振器Hub扭转角Colormap图

图11 减振器Hub扭振阶次图
对于4.5,6,7.5及9阶在不同转速引起的扭转共振,三维扭振计算结果中的共振阶次、对应临界转速与扭振角分别为4.5阶/5 750 r·min-1/0.341°,6阶/4 400 r·min-1/0.136°,7.5阶/3 400 r·min-1/0.093°,9阶/2 800 r·min-1/0.065°,对应的扭振频率均为430 Hz左右,与自由模态分析基本吻合。
2.3 试验验证
在台架上对发动机进行曲轴系皮带轮端扭振测试,并将实测数据与计算结果进行对比。曲轴扭振各主阶次振幅随转速的变化见图12。从图中可以看出扭振阶次4.5,6,7.5及9阶对应的临界转速与扭振角,具体数值见表4。
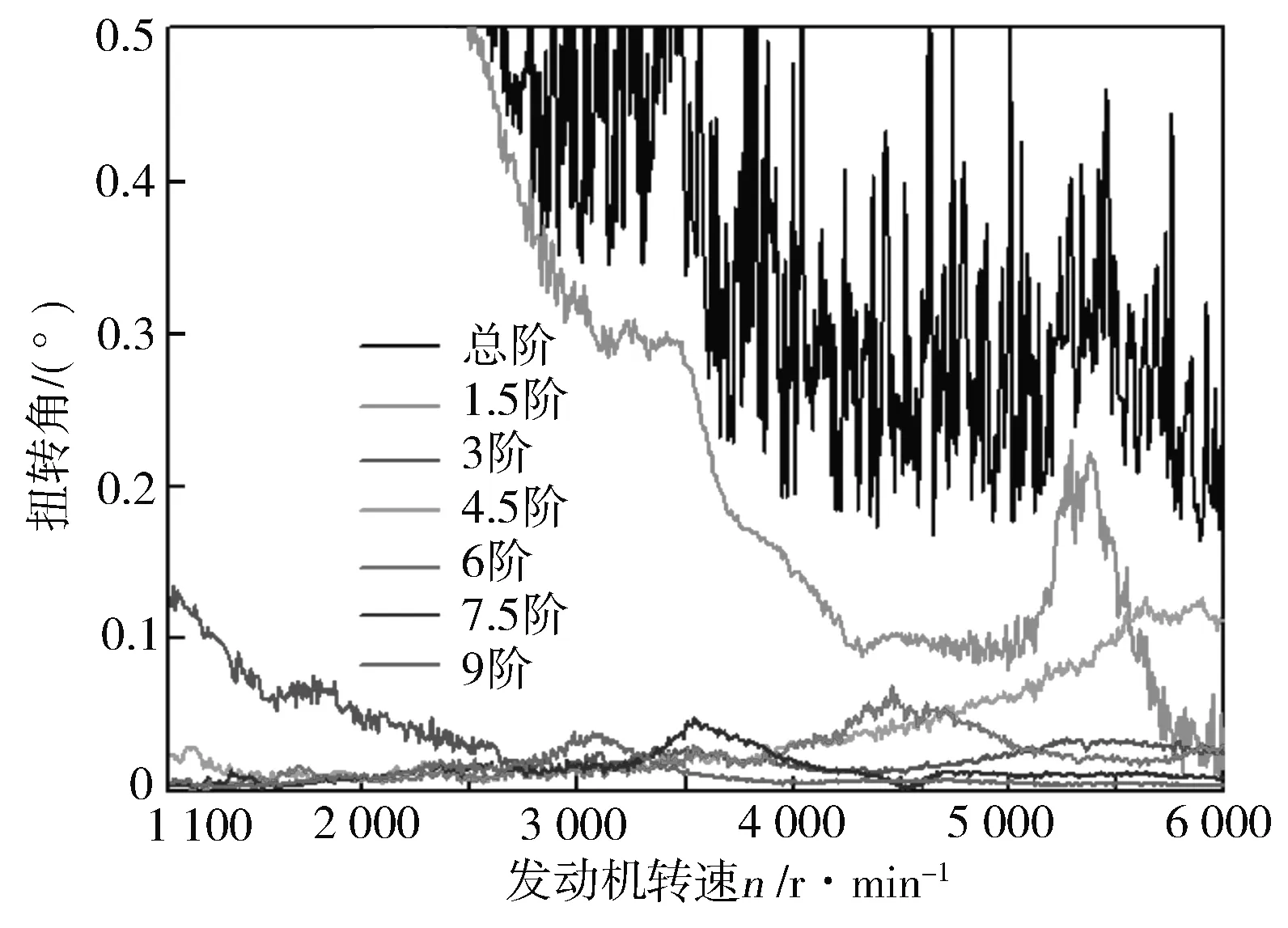
图12 曲轴扭振角转速
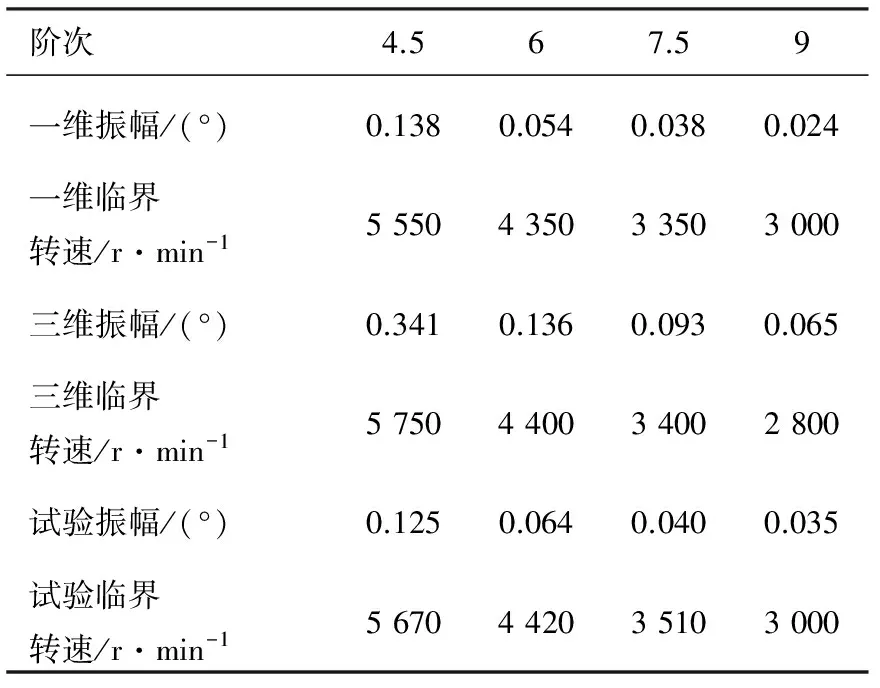
阶次4.567.59一维振幅/(°)0.1380.0540.0380.024一维临界转速/r·min-15550435033503000三维振幅/(°)0.3410.1360.0930.065三维临界转速/r·min-15750440034002800试验振幅/(°)0.1250.0640.0400.035试验临界转速/r·min-15670442035103000
减振器Hub扭振转角一维和三维计算值与试验值对比见表4,各阶次计算值与测试值吻合较好。
通过对比不难发现,三维模型计算结果振动幅值的精度反而略低于一维计算模型,这是因为三维计算模型需要的边界条件较难处理(如轴承油膜润滑、曲轴和缸体有限元模型缩减等);稳态转速控制较为复杂,转速间隔也较大,因此计算误差相对难以控制,需要更为精准的建模。出于对计算时间和计算精度的考虑,以下对该三缸机的扭振分析,均以一维计算模型为基础。
需要特别说明的是,从扭转角-转速曲线可以看出,1.5阶次5 300 ~5 500r/min范围内存在振幅峰值,经对试验台架的整体分析,发现出此峰值是由于曲轴转速达到了传感器支架的固有频率而发生的共振引起,并非是曲轴扭振共振,属于测试误差范畴。
3 曲轴系扭振分析与探究
3.1 三缸机曲轴系扭振特性
众所周知,三缸机的平衡性和扭振问题相对于四缸机更难以解决。较四缸机而言,三缸机的发火间隔角较大,曲轴受到的激励间隔也就增大,造成低速时运转平顺性差,转速波动较大,只有当转速逐渐升高,转速波动才有所缓解;而且低速时各缸膨胀做功均匀性较差,从而导致了在该低速范围内转速波动较大,转速越低,波动越大。
三缸机的点火间隔角为240°,点火频率为曲轴转速的1.5倍,因此曲轴扭振的1.5阶分量实则代表点火做功激励引起的强迫振动。而1.5阶作为三缸机的主阶次,在研究三缸机扭振特性时需重点关注。
图13示出减振器Hub端扭转角1.5阶分量在各个转速下占扭振总阶比例。可以看出:低转速段,三缸机曲轴扭转振幅主要成分是1.5阶分量,而1.5阶在该转速区间并未发生扭转共振,说明低速段振幅的主要成分是强迫振动激励造成的转速波动;高转速段,点火激励所占扭转振幅比例很低,此时曲轴扭振振幅的主要成分是高阶次扭转共振。

图13 1.5阶分量占扭振总阶比例
3.2 三缸机曲轴系扭振优化分析
根据以往工程经验和当前曲轴工艺水平可知,目前发动机曲轴系的一阶扭转固有频率基本在200~350 Hz,所以对于三缸机,在6 000 r/min以内其1.5阶不会发生扭转共振。因此,对于三缸机的扭振控制,应该控制低速段转速波动和高速段高阶次的扭转共振。
对于低速段转速波动,最有效的方式为增大系统转动惯量,通常增加飞轮惯量。改变一维模型的飞轮惯量(原系统飞轮惯量0.20 kg·m2),减振器Hub端扭振计算结果见图14。
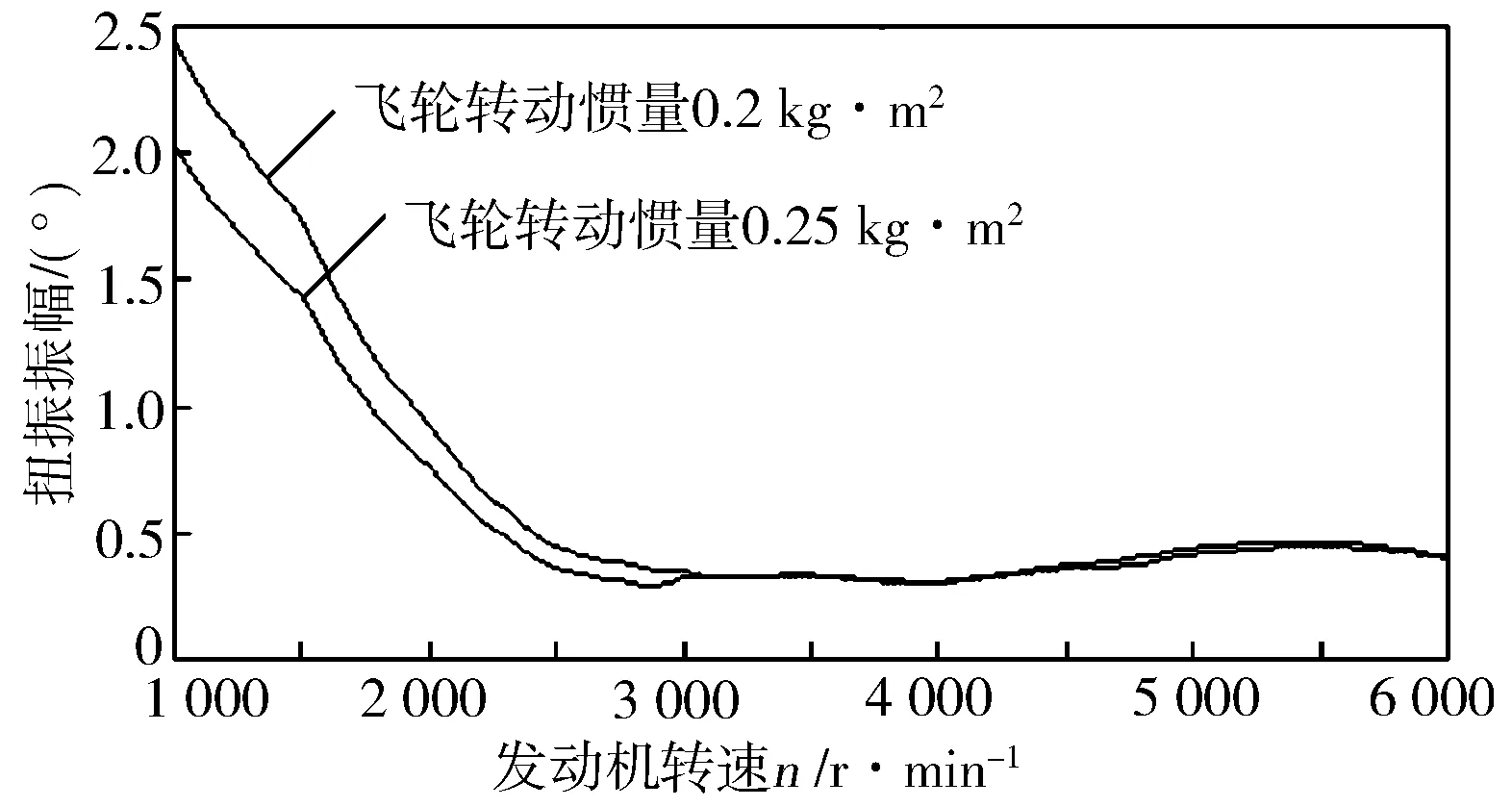
图14 增加惯量前后Hub端振幅对比
但系统惯量的增加会导致高阶次共振振幅略微增大,同时还会增加发动机质量,因此对于飞轮转动惯量的选取应经过严格的分析与计算。
对于降低高速段高阶次扭转共振振幅,目前应用最多的方式为在曲轴前端安装曲轴扭振减振器(减振皮带轮),采用合适的设计参数可以起到消减曲轴扭振共振振幅和吸收曲轴扭振产生的能量的作用,并且能够改善前端附件轮系的工作状态。本研究试验所采用的三缸机在高阶次的扭振表现较为优秀,在共振阶次4.5阶、6阶、7.5阶和9阶上,均将共振振幅限制在0.2°内,而且在汽油机常用工作转速1 300~3 000 r/min内均未发生共振。
观察该三缸机的曲轴减振皮带轮,发现其结构与常见的外圈惯量环直接承载皮带的减振器(承载式减振器,见图15a)不同,它是由减振器轮毂Hub承载皮带(非承载式减振器,见图15b),而惯量环为自由端。下面将两种结构形式的减振皮带轮对曲轴前端自由端的减振效果应用一维模型进行验证。

图15 曲轴扭振减振器
3.3 两种减振器的减振效果对比
承载式减振器相对于非承载式减振器改变了扭振模型前端所受载荷的位置(见图16)。

图16 曲轴扭振减振器简化模型
为了对比两种方案的减振效果,以减振器结构形式为自变量,保证承载式减振器的Ring、橡胶环和Hub的参数与原减振器一致,计算中减振器形式的变化在扭振计算模型中不体现为参数的变化。因此,所需关注的加载皮带端的扭转角则从轮毂Hub变为了惯量环Ring,这样,以原一维计算模型为基础,在计算结果中提取惯量环Ring的计算结果与Hub进行对比。
计算结果显示曲轴系扭转振动固有频率与原模型一致(固有频率不受外部载荷和激励影响),因此主阶次1.5阶和3阶仍不发生共振,安装两种减振皮带轮时的4.5阶、6阶、7.5阶和9阶皮带轮加载位置扭转角对比结果见图17。

图17 曲轴扭振减振器承载皮带端扭转角
从计算结果可以明确得出,本机采用的非承载式减振皮带轮对曲轴前端自由端的扭振降低效果显著,能将自由端共振振幅峰值衰减35%~40%,同时从图18也能看出加载位置的转速均匀度有明显改善,确认为本机降低曲轴系扭振危害的一个有效设计。

图18 皮带加载位置转速均匀度
4 结束语
采用一维和三维多体系统仿真体系分析了曲轴系的扭振特性、自振固有频率、振型、强迫振动扭转角度及转速均匀度,计算结果显示,基于虚拟样机的扭振分析结果与试验测试结果基本一致,且一维模型计算精度足以很好地预测发动机实际工作过程可能产生的扭振问题。由计算结果和试验数据分析了三缸机曲轴系的扭振特性,并对三缸机扭振的研究方法和控制路线进行了说明,即控制其低速段1.5阶分量强迫振动激励引起的转速波动和高速段高阶次的曲轴扭转共振振幅;同时,该三缸机对非承载式减振皮带轮的应用也有效降低了曲轴自由端的扭振危害。本次建模无论在有限元模型还是多体动力学模型上都保持了很高的计算精度,从而保证了计算结果的准确性。该款发动机在NVH设计上的先进理念,为国内同类自主产品的开发设计与改进提供了重要的参考依据。
参考文献:
[1] 李克强.汽车技术的发展动向及我国的对策[J].汽车工程,2009,31(11):1005-1016.
[2] 张芳,王必璠,李显戴.车用发动机扭转振动的分析与控制[J].汽车科技,2011(2):47-51.
[3] Maciej Zawisza.Energy Loss and the Choice of Damper of Torsional Vibration Combustion Engines[J].Trans Tech Publications,2015,236:188-195.
[4] Jagielowicz-Ryznar C.The Impact of Complex Forcing on the Viscous Torsional Vibration Damper’s Work in the Crankshaft of the Rotating Combustion Engine[J].Int.J.of Applied Mechanics and Engineering,2016,21(4):1017-1023.
[5] Kim G W.Piezoelectric energy harvesting from torsional vibration in internal combustion engines[J].International Journal of Automotive Technology,2015,16(4):645-651.
[6] Dereszewski M.Monitoring of torsional vibration of a crankshaft by instantaneous angular speed obserbations[J].Journal of KONES Powertrain and Transport,2016,23(1):99-106.
[7] Chiliński B,Zawisza M.Modelling of lateral-torsional vibrations of the crank system with a damper of vibrations[J].Vibroengineering Procedia,2015,10(6):61-65.
[8] Kareem B.Mechanical failure analysis of automobile crankshafts under service reconditioned modeling approach[J].Engineering Failure Analysis,2017,80:87-101.
[9] 李静,王东方,繆小东,等.发动机曲轴扭振仿真分析与研究[J].机械设计与制造工程,2017,46(5):41-45.
[10] 上官文斌,陈超,段小成,等.发动机曲轴系扭转振动建模与实测分析[J].振动、测试与诊断,2012,32(4):560-567.
[11] 王祺.内燃机轴系扭转振动[M].大连:大连理工大学出版社,1991.
[12] 盛宏玉.结构动力学[M].合肥:合肥工业大学出版社,2005.

