一种基于双喷嘴模型的涡轮等效流通面积计算方法
李梦钰,石磊,张慧龑,李华雷,刘胜,杨震寰
(1.上海交通大学动力机械与工程教育部重点试验室,上海 200240; 2.中国航发商用航空发动机有限公司,上海 201109;3.中国北方发动机研究所(天津),天津 300400)
涡轮增压技术在保证结构紧凑性的情况下可缩小排量,改善缸内燃烧过程,进一步提高柴油机的功率密度,降低柴油机油耗、排放和噪声[1-2]。而涡轮等效流通面积的计算对涡轮特性的描述和涡轮增压系统与柴油机的匹配具有重要意义:一方面,利用涡轮等效流通面积可以计算涡轮膨胀比与流量的关系,描述涡轮流通特性和做功能力;另一方面,对于涡轮增压系统与柴油机的匹配,特别是变海拔匹配,通过压气机耗功需求和柴油机特性计算全工况涡轮等效流通面积需求,可以确定匹配点涡轮增压器的选型和全工况涡轮旁通阀调节目标。为计算涡轮等效流通面积,学者基于热力学基本方程提出较多一维涡轮简化模型,目前应用范围较广的是简单涡轮模型[4],将涡轮等效成单喷嘴,认为在相同流量下,喷嘴面积产生与涡轮相等的压降。但其只适用于中等膨胀比,膨胀比到达1.89之后,简单喷嘴模型计算的涡轮流量增加缓慢,会出现阻塞现象。事实上,实际涡轮工作过程分为静叶和动叶两阶段,膨胀比可达3.0[5]。之后又衍生出简单喷嘴模型的替代方法[6],认为其产生的压降是涡轮实际压降的一半。此方法解决了临界膨胀比问题,但喷嘴出口处的压力实际上是静叶与动叶之间的压力,不利于计算涡轮出口压力演变和分析涡轮做功能力。为解决上述问题,Payri等[7-8]提出双喷嘴模型,之后Eriksson[9]进行了改进,但分别局限于气体在两个喷嘴膨胀过程中压降相等或膨胀比相等的假设。
本研究在双喷嘴模型的基础上,提出了根据反动度计算静叶喷嘴出口压力,分别确认静叶和动叶喷嘴处膨胀比,进一步计算涡轮等效流通面积的方法。为验证此改进方法描述涡轮流通特性的准确性,利用GT-Power软件搭建柴油机性能仿真模型,根据计算得到的面积反算相应工况下涡前涡后的气体状态参数并得到涡轮流通特性曲线,同时与简单喷嘴模型计算结果作对比。为验证此改进方法描述涡轮做功能力的准确性,基于计算得出的涡轮等效流通面积和变海拔涡轮面积关系式,为某6缸柴油机确定了涡轮变海拔匹配方案,考察增压压力恢复情况。
1 计算模型
根据Payri的理论[7-8],气体在径流式涡轮中的热力过程实际上是在静叶和动叶的两次膨胀,其简化模型见图1,热力过程见图2。由此可将静叶和动叶分别视为等效喷嘴,具有和理想喷嘴相同的流通特性。排气从涡轮入口处进入静叶喷嘴,进行第一次膨胀,然后经过稳压腔积聚质量流量,再经动叶喷嘴进行第二次膨胀并做功,最后通过涡轮出口排入大气。将气体在径流式涡轮中的流动过程视为准稳态流动。
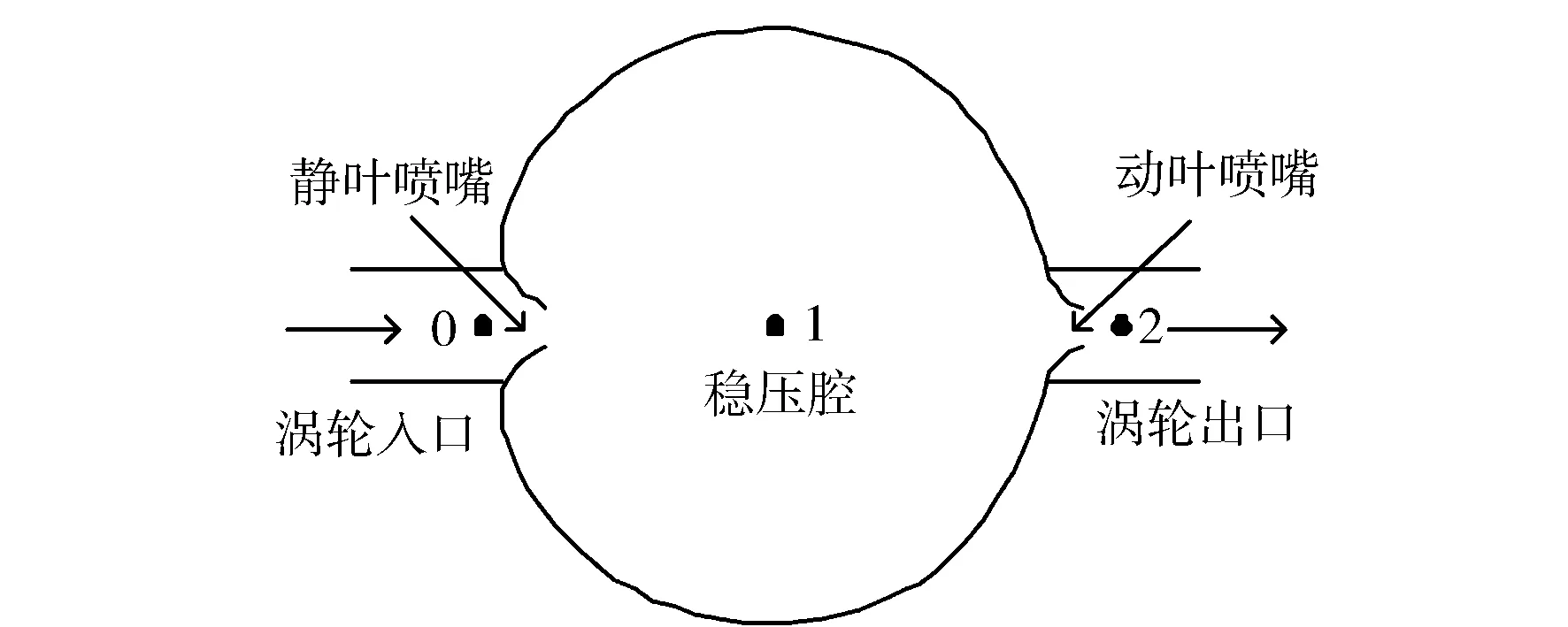
图1 径流式涡轮简化模型
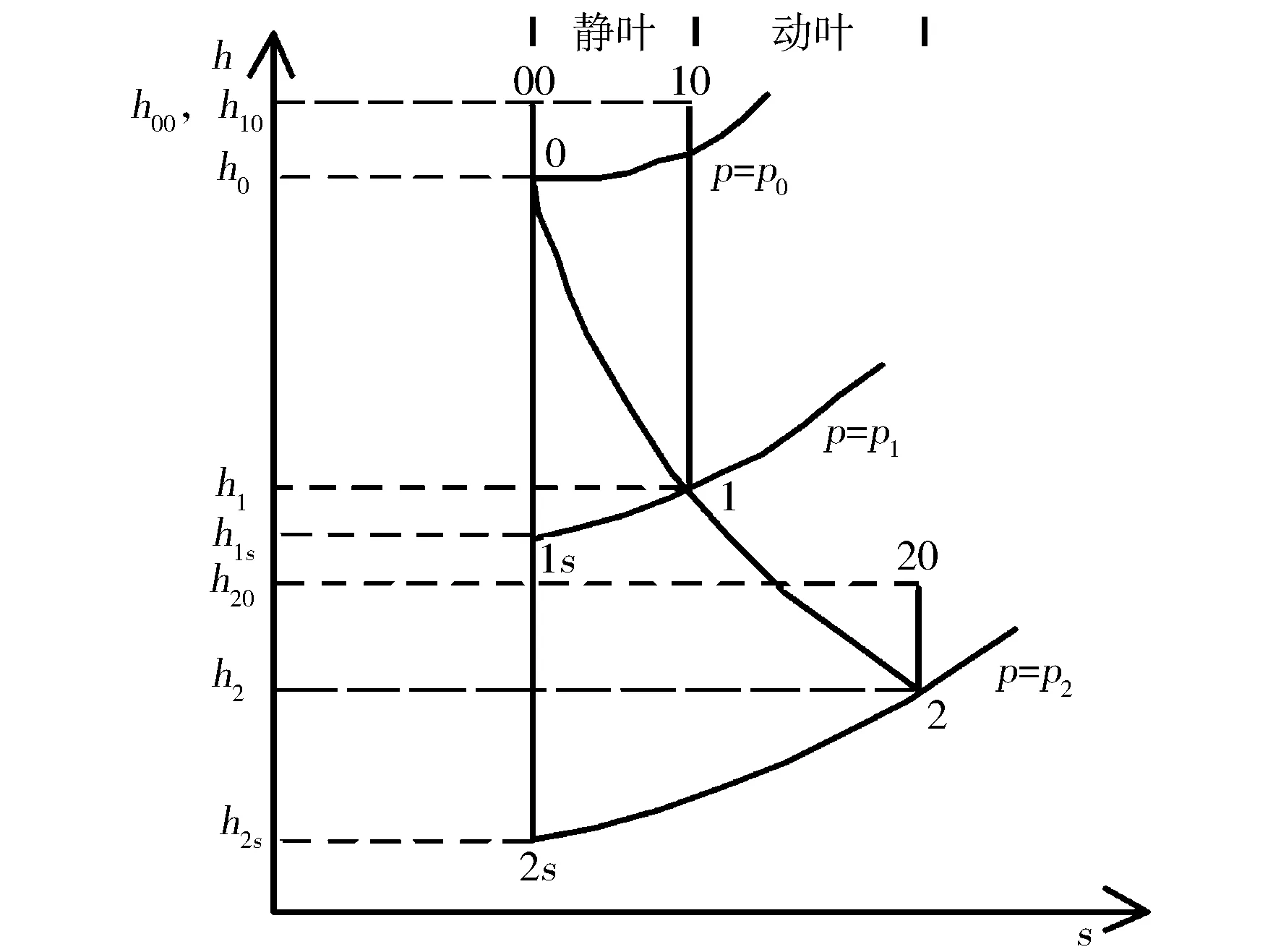
图2 径流式涡轮热力过程
1.1 涡轮反动度计算
反动度是衡量气体的膨胀过程在动、静叶处如何分配的参数。反动度大意味着气体在动叶的膨胀份额更大。目前,比较常见的反动度定义方法有两种:一种是由静压定义的反动度,为动叶静压降与级的压降之比;一种是由静焓定义的反动度,为动叶静焓降与级总能量转换之比。本研究选取后者:
(1)
式中:Λ为反动度;h表示焓;下标中第一个位置的0,1,2分别表示静叶入口、静叶出口和动叶出口,下同;下标中第二个位置的0表示滞止焓,如没有则为静焓。
涡轮动叶入口和出口处的速度三角形见图3,其中c为气流绝对速度,它的径向和轴向分速度分别为cr和cα。u表示动叶叶尖速度,ω为气体相对于叶片的速度。所以有
(2)
又因为气流在静叶只膨胀不做功,有静叶喷嘴入口和出口滞止焓相等,即h00=h10,代入式(2)中可得
(3)
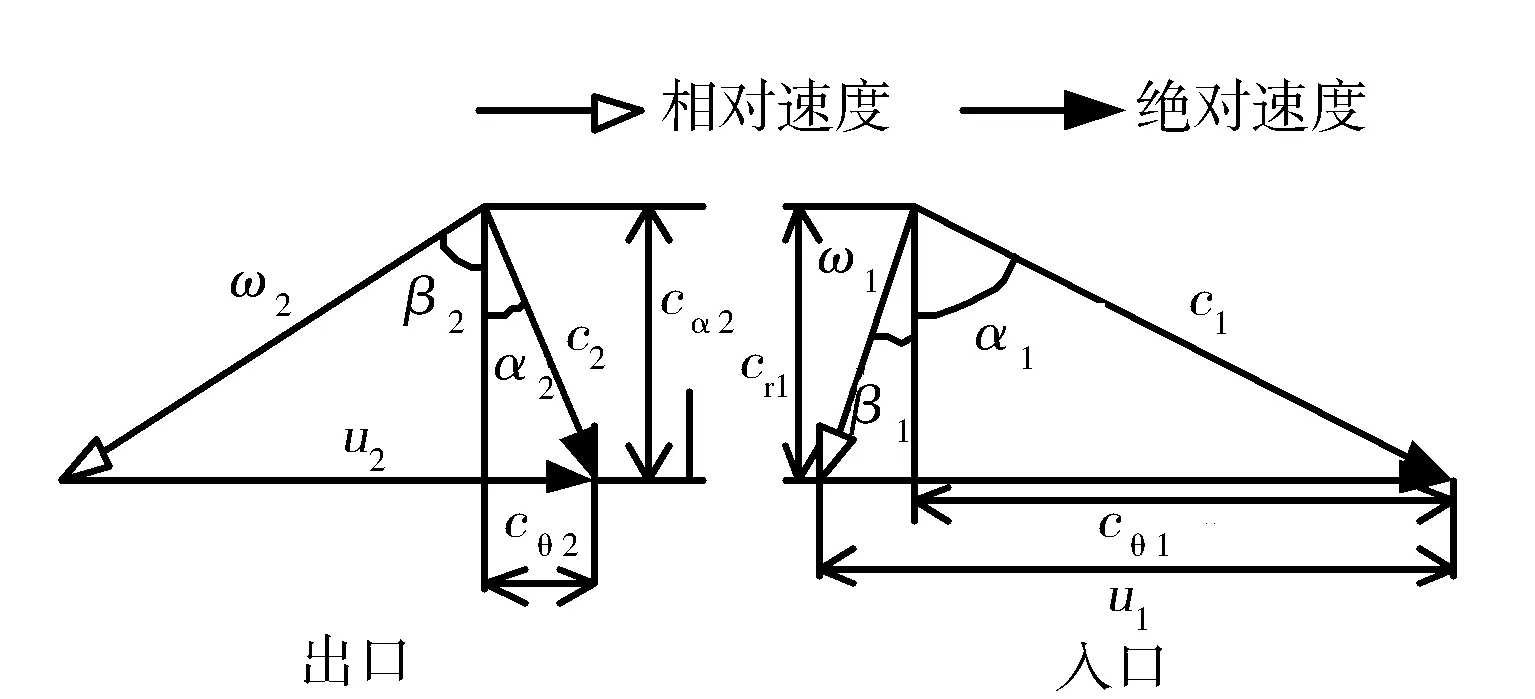
图3 动叶出口和入口速度三角形[4]
将发动机排气视为理想气体,则有
h10-h20=cpT10-T20。
(4)
式中:cp为排气的比定压热容;T表示温度,下标中第二个位置的0表示总温。将式(3)、式(4)与式(1)联立得
(5)
根据叶轮机械欧拉方程和速度三角形,则有
(6)
c12=cθ12+cr12,
(7)
c22=cθ22+cα22。
(8)
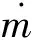
(9)
最后考虑动叶出口气体轴向分速度等于入口气体径向分速度,即cr1=cα2,最终化简得
(10)
如果是固定截面涡轮,静叶出口相对速度ω1与垂直线的夹角β1=0,cθ1=u1,所以反动度Λ=0.5。
1.2 静叶喷嘴出口压力计算
根据式(1),将涡轮内工质视为理想气体,可得
(11)
将气体在静叶、动叶和整个级之间的膨胀过程视为多变过程,多变指数分别为k,g和n,有
(12)
其中p表示气体压力。整理得
(13)
其中n可通过下式计算:
(14)
但k和g未知,只有式(12)无法求出两个变量,需引入其他假设。分别讨论Λ>0.5,Λ=0.5,Λ<0.5的情况,热力过程见图4。Λ=0.5时,两个喷嘴处气体焓降相同,因为静叶喷嘴处的气体流速更快,所以比动叶喷嘴有更大的熵增。由此可确定实际过程的工作曲线,进一步确定静叶喷嘴出口压力p1k-g(见图4a)。由图可以看出,假设气体在静叶喷嘴处作多变指数为k′的膨胀,在动叶喷嘴处作绝热膨胀,得到静叶喷嘴出口压力为p1k′-γ,比假设全部过程绝热膨胀求得的p1γ和假设全部过程为多变指数为n的膨胀求得的p1n更接近实际压力p1k-g。事实上,当涡轮等效流通面积越小时,静叶喷嘴处气体因摩擦造成的不可逆损失越大,在图中表现为0—1曲线更倾斜,p1k-g和p1k′-γ之间的差距更小,假设更精确。同理,对于Λ>0.5(动叶喷嘴处气体焓降大于静叶喷嘴)和Λ<0.5(动叶喷嘴处气体焓降小于静叶喷嘴)的情况,由图4b和图4c可以看出,p1k-g总是落在p1k′-γ与p1γ之间,且均靠近p1k′-γ一侧。所以,综合考虑上述3种情况,为计算静叶喷嘴出口压力,可假设气体在动叶喷嘴处进行绝热膨胀,即g=γ,代入式(13)中求得静叶喷嘴处多变指数k′:
(15)
进一步求得静叶喷嘴出口压力p1:
(16)
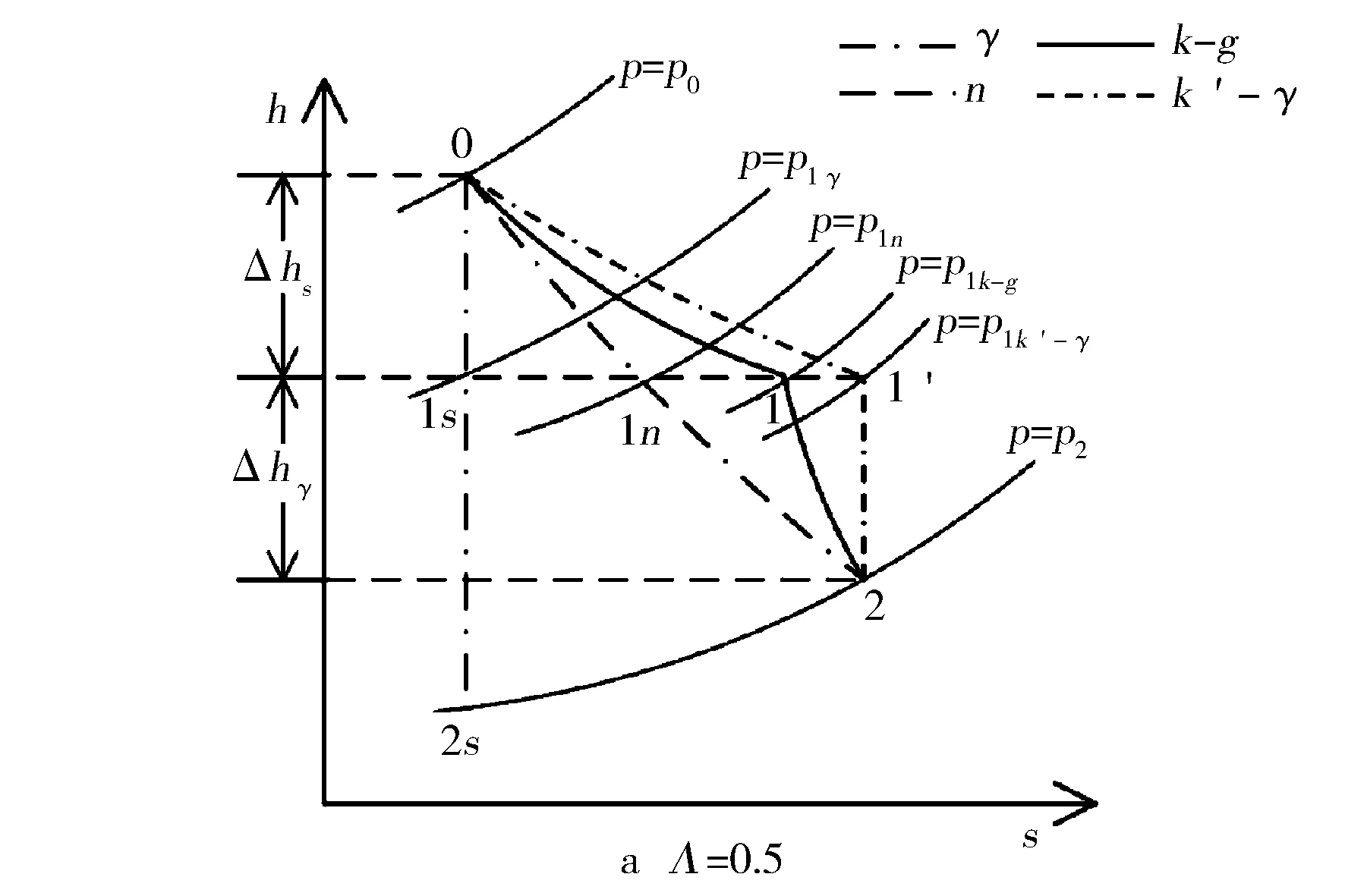
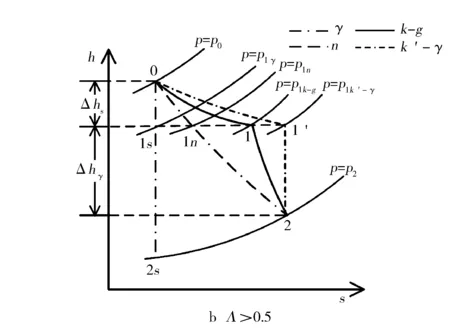
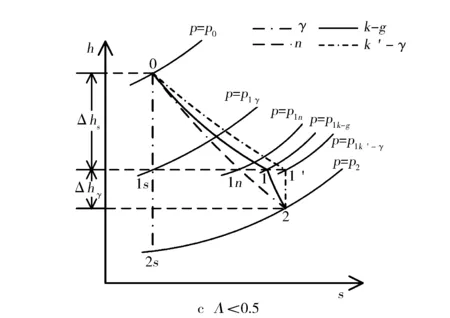
图4 不同反动度下涡轮热力过程
1.3 涡轮等效流通面积计算
如前所述,利用式(10)和式(16)求出涡轮反动度和静叶喷嘴出口压力之后,可确定在静叶喷嘴和动叶喷嘴处的膨胀比,再代入到Payri提出的公式[7-8]中,可得静叶喷嘴和动叶喷嘴的等效流通面积。
(17)
(18)
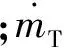
(19)
2 计算结果及验证
2.1 双喷嘴模型的GT-Power仿真验证
2.1.1计算结果
将某6缸柴油机(主要参数见表1)的试验数据代入上述公式,得到外特性工况不同转速(从最大扭矩点转速到标定功率转速)的涡轮等效流通面积(见图5)。同时利用简单喷嘴模型[4]计算相同工况下的涡轮等效流通面积,将两者进行对比。

表1 试验发动机主要参数

图5 涡轮等效流通面积
由图5可以看出,当发动机转速从最大扭矩点转速提高到标定功率转速时,静叶喷嘴面积、动叶喷嘴面积以及涡轮等效流通面积均上升。这是因为小涡轮等效流通面积对应大膨胀比,在涡轮效率变化不大的情况下,可提供更大的涡轮功,进一步提高压气机压比,弥补低转速时发动机进气量不足的情况。反之,高转速时发动机进气量充足,涡轮等效流通面积应增大,否则可能出现压比过高、缸内最高燃烧压力超限、涡轮增压器超速的现象。
此外,由图5还可以发现静叶喷嘴面积小于动叶喷嘴面积,更接近涡轮等效流通面积。表明在整个涡轮的气体膨胀过程中,静叶喷嘴处的膨胀比要高于动叶喷嘴(见图6),这与双喷嘴模型推导过程中静叶喷嘴不可逆损失大于动叶喷嘴的假设相符。此外,比较简单喷嘴和双喷嘴模型的涡轮等效流通面积计算结果,发现简单喷嘴模型计算结果偏小。表明在流量相同条件下,简单喷嘴模型需要用更小的面积,才能达到与双喷嘴模型相同的膨胀比,也就是说,简单喷嘴模型对废气能量利用率更低,不可逆损失更大,这是由双喷嘴模型假设动叶喷嘴处膨胀绝热导致的。

图6 双喷嘴模型涡轮膨胀比
2.1.2模型建立与校核
为便于验证双喷嘴涡轮流通特性模型的计算结果,利用GT-Power软件搭建某单级涡轮增压柴油机的仿真计算模型(见图7)。其中,气缸燃烧模型采用三韦伯放热规律函数[11];缸内传热过程用woschni模型[12]描述;利用一维简化方式设立进排气管道;中冷器效果通过增大Pipe模块的管壁面积和传热系数以及设定其目标壁温实现;将MAP图谱以离散化方式输入到涡轮增压器模型中。变海拔环境通过修改入口、出口气体压力和温度模拟。
利用上述GT-Power仿真模型计算原机在最大扭矩点转速和标定功率转速的外特性性能参数,计算结果与试验值之间的误差见图8。可以看出,两个工况下主要参数的相对误差均小于5%,表明此柴油机单涡轮增压器系统仿真模型有较高精度,可用于柴油机性能分析研究。
2.1.3验证结果
将原机增压器流通特性用前述双喷嘴模型计算得到的涡轮等效流通面积表示,并输入GT-Power仿真模型,反算得到外特性工况下涡轮工作曲线以及柴油机性能数据,与简单喷嘴模型计算结果进行比较,验证双喷嘴涡轮流通特性模型的准确性和适用范围(见图9和图10)。
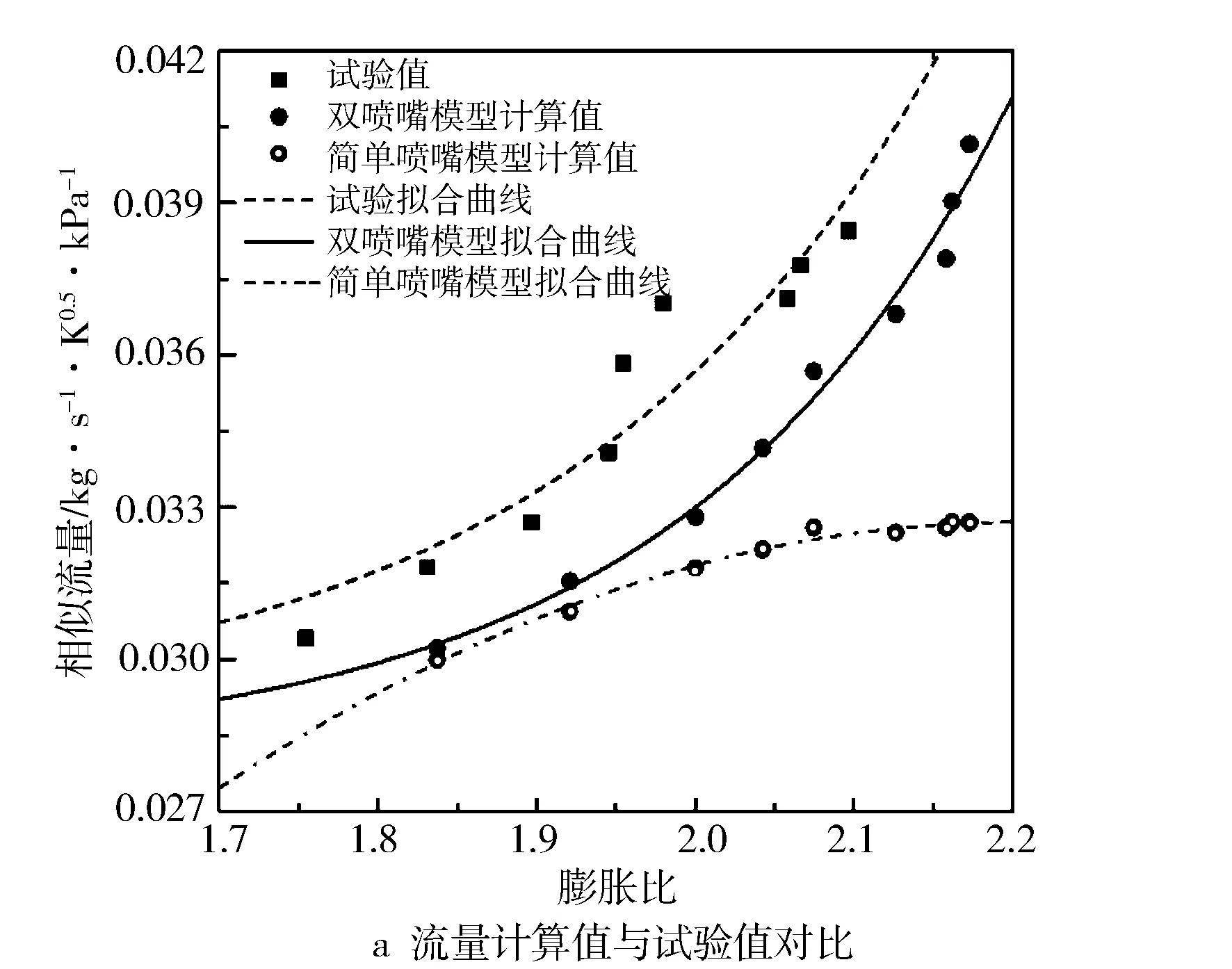
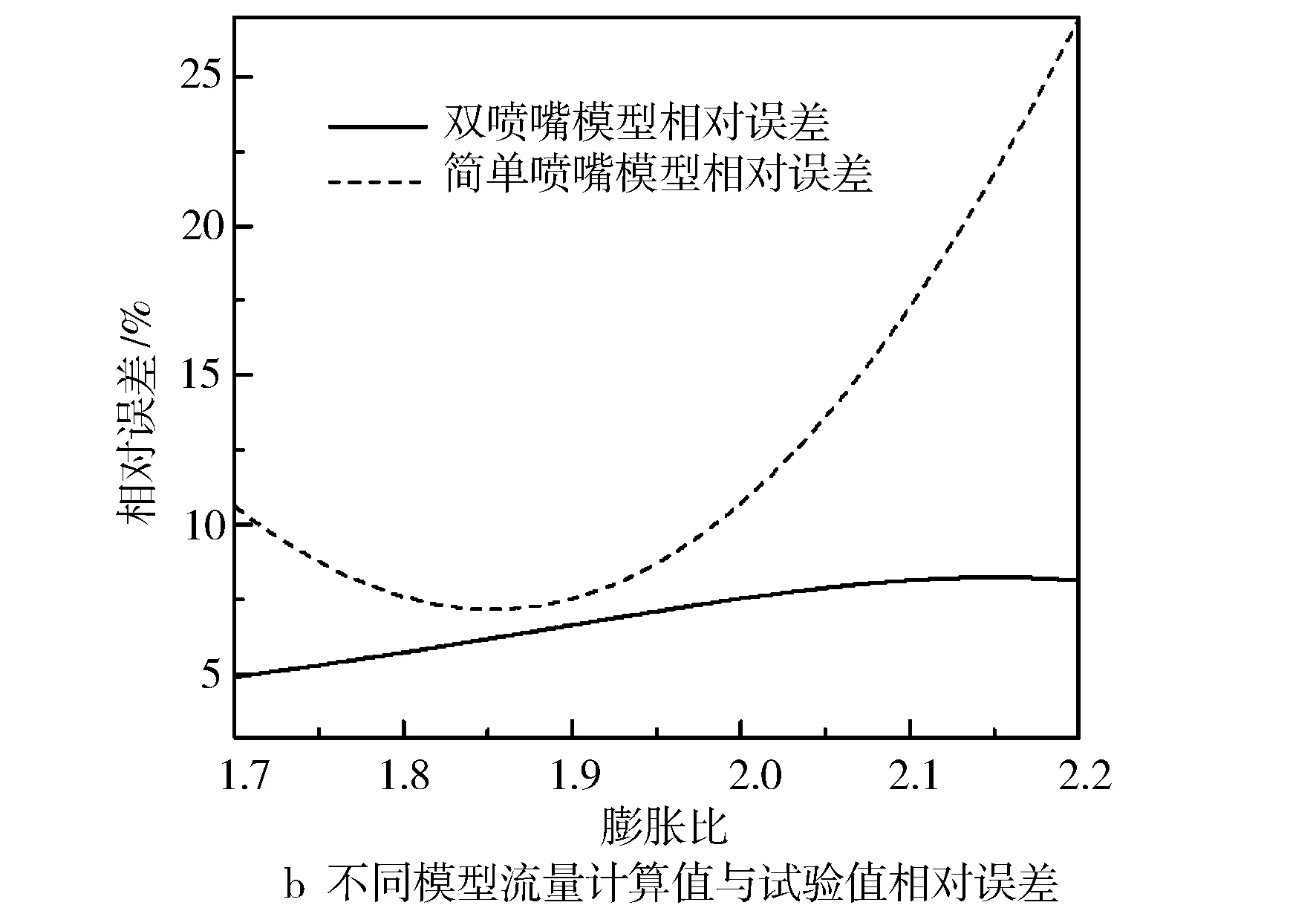
图9 涡轮特性对比
图9比较了经计算和试验得出的外特性不同转速下涡轮的膨胀比和流量,并利用计算得到的工作点得出涡轮特性拟合曲线。得到的拟合曲线与一般涡轮特性曲线稍有区别,描述的是涡轮在不同流通面积下对应的膨胀比和流量。双喷嘴模型拟合结果与试验得到的曲线相对误差不超过9%,且在低流量时的误差要比高流量时小一些,表明双喷嘴模型可用于表征涡轮特性,且在低流量时准确性更高。这是因为在高流量时,涡轮实际的等效流通面积较大,故在静叶喷嘴处气体膨胀的不可逆损失较小。而又如前1.2节所述,已经得出在静叶喷嘴处的不可逆损失越大,动叶喷嘴膨胀过程越接近绝热膨胀假设,静叶喷嘴出口压力计算值越接近实际值的结论。所以高流量时静叶喷嘴出口压力的计算不如低流量时准确,进一步影响了涡轮等效面积的计算。简单喷嘴模型涡轮特性计算值低于双喷嘴模型,因为如2.1.1节所述,简单喷嘴模型涡轮等效面积计算值更小,所以在相同膨胀比下,流通能力差,由GT-Power计算出的流量更低,与试验值误差更大。特别是在高膨胀比(大于2.1)区域,由于流量增长缓慢,简单喷嘴模型与试验值的误差在15%以上。综上,双喷嘴模型在准确度和适用范围方面均优于简单喷嘴模型。
图10示出涡前温度和涡后温度的计算结果和试验数据的比较。
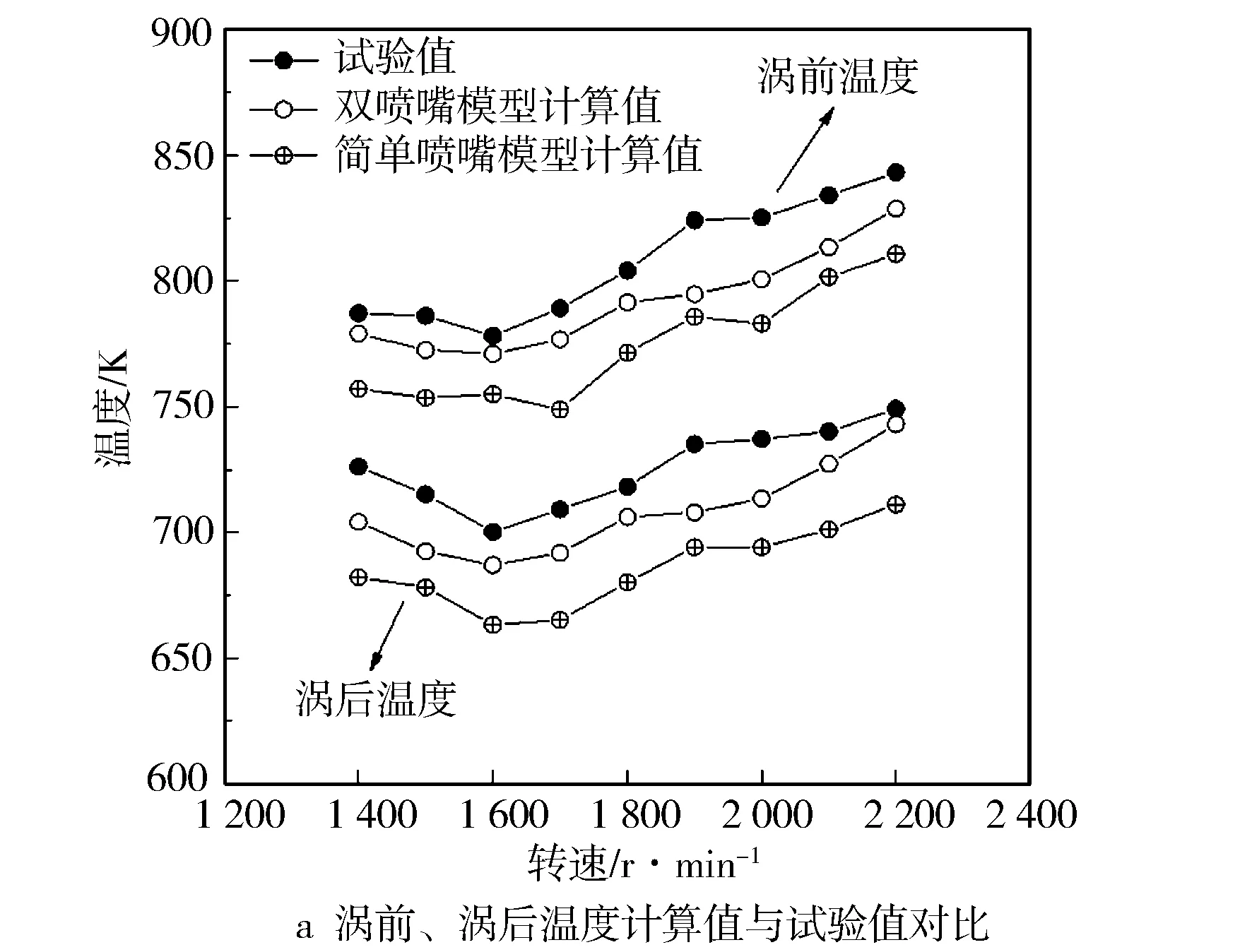
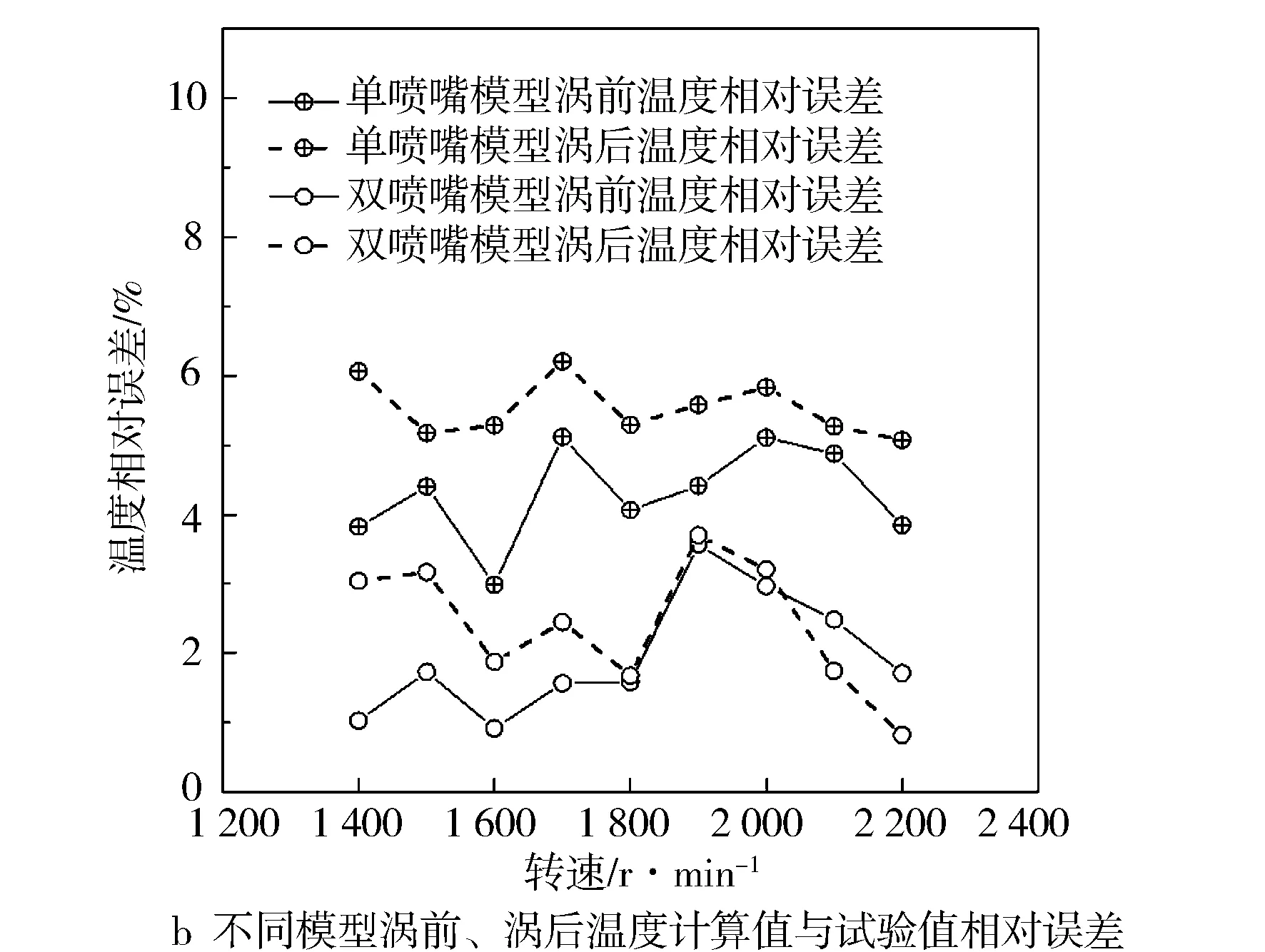
图10 涡前、涡后温度计算与试验结果对比
从图10可以看出简单喷嘴模型计算结果误差大于双喷嘴模型,前者误差在4%~6%之间,后者相对误差在4%以内,证明双喷嘴涡轮流通特性模型具有较高的精度,可以用来再现涡轮的工作过程。
2.2 双喷嘴模型的变海拔匹配验证
在涡轮增压系统与柴油机变海拔匹配过程中,海拔变化将引起环境压力即压气机入口压力变化,如果要确保不同海拔下增压压力均恢复到平原水平,压气机压比以及涡轮做功能力需要有一定的调节范围,这通过涡轮旁通阀调节涡轮流量,进一步调节涡轮等效流通面积实现。若只考虑平原涡轮等效流通面积,在高海拔时不加以调节,容易造成高海拔时涡轮等效流通面积过大,涡轮膨胀功和压气机压比不足,难以实现高海拔增压压力恢复。因此,需要利用本研究提出的涡轮流通特性模型计算出平原涡轮等效流通面积,再结合变海拔涡轮面积关系得到全海拔涡轮等效流通面积需求,通过计算全海拔涡轮等效流通面积下对应的增压压力,验证增压压力是否恢复到平原水平,证明涡轮等效流通面积的计算值满足要求,进一步证明本研究提出的涡轮流通特性模型的正确性与实用性。
2.2.1计算结果
根据李华雷等[13-15]提出的基于增压压力恢复的变海拔涡轮匹配方法,则有
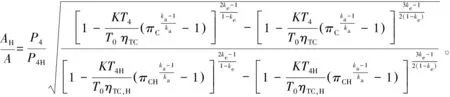
(20)
式中:角标0和4分别表示涡前和环境状态;H代表高原状态;πC为压比;ka和ke分别为空气和排气的绝热指数;ηTC为增压系统总效率。
将2.1.1节所述计算结果,即利用双喷嘴涡轮模型计算得到的某柴油机在平原外特性工况下最大扭矩点转速和标定功率转速的涡轮等效流通面积A1和A2,代入到式(20)中,可确定该柴油机在高原对应工况下为实现增压压力恢复所需的涡轮等效面积A1H和A2H,进一步得到变海拔、变工况所需的涡轮等效流通面积变化范围(见图11)。可以看出,随着海拔降低,压比需求增大,涡轮等效流通面积变小,且面积最小值和最大值分别出现在3 000 m最大扭矩点转速(匹配点)和平原标定功率转速工况。这是因为高海拔低转速时柴油机进气量最少,因此,需要最小的涡轮等效流通面积,旁通阀门应全部关闭,保证涡轮有足够的膨胀功输出,带动压气机提供高压比,因此,此点也经常作为涡轮选型的匹配点。而在低海拔高转速工况,柴油机进气量较大,需调节旁通阀开度,令涡轮等效面积达到最大值,否则将出现涡轮超速、压比超限现象,因此,此点将作为阀门调节规律中的开度最大点。
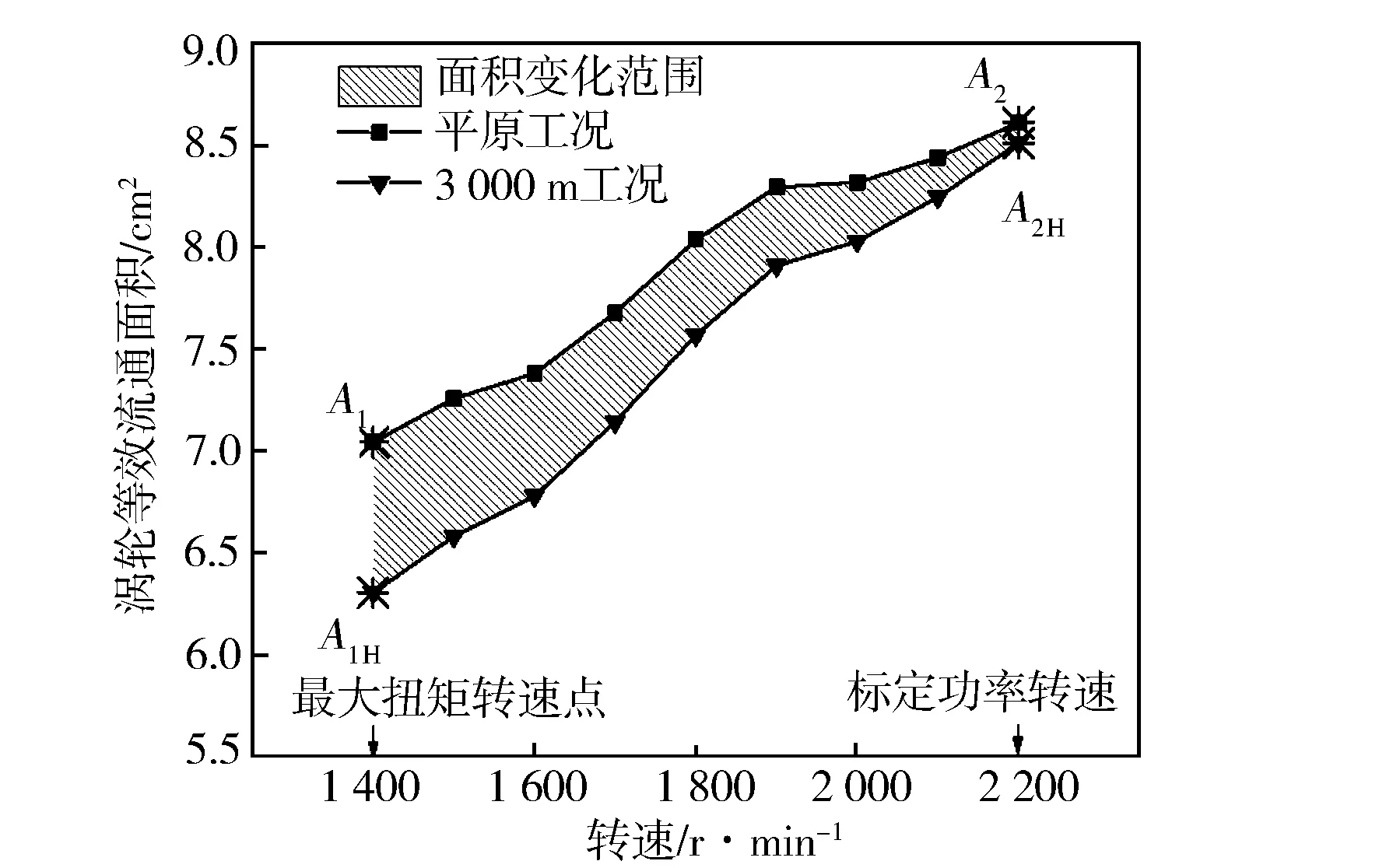
图11 变海拔外特性工况涡轮等效面积变化范围
2.2.2验证结果
将全海拔涡轮等效流通面积计算值代入2.1.2节所述某柴油机性能仿真模型中,验证柴油机变海拔增压压力恢复情况(见图12)。可以看出在3 000 m范围内,该柴油机从最大扭矩点转速到标定功率转速的增压压力均恢复到了平原水平,证明基于双喷嘴涡轮流通特性模型以及变海拔等效面积关系式计算得出的高原涡轮等效流通面积可以满足变海拔增压压力恢复需求,进一步说明双喷嘴涡轮流通特性模型可准确表征涡轮做功能力。此外,在低于1 400 r/min的低转速范围,该柴油机未能实现增压压力完全恢复,这与匹配点选择有关,匹配点涡轮等效流通面积为调节范围内的最小值,无法进一步减小为更低转速提供足够压比,若想实现更大范围内压力恢复,应重新调整匹配点向更高海拔更低转速移动。
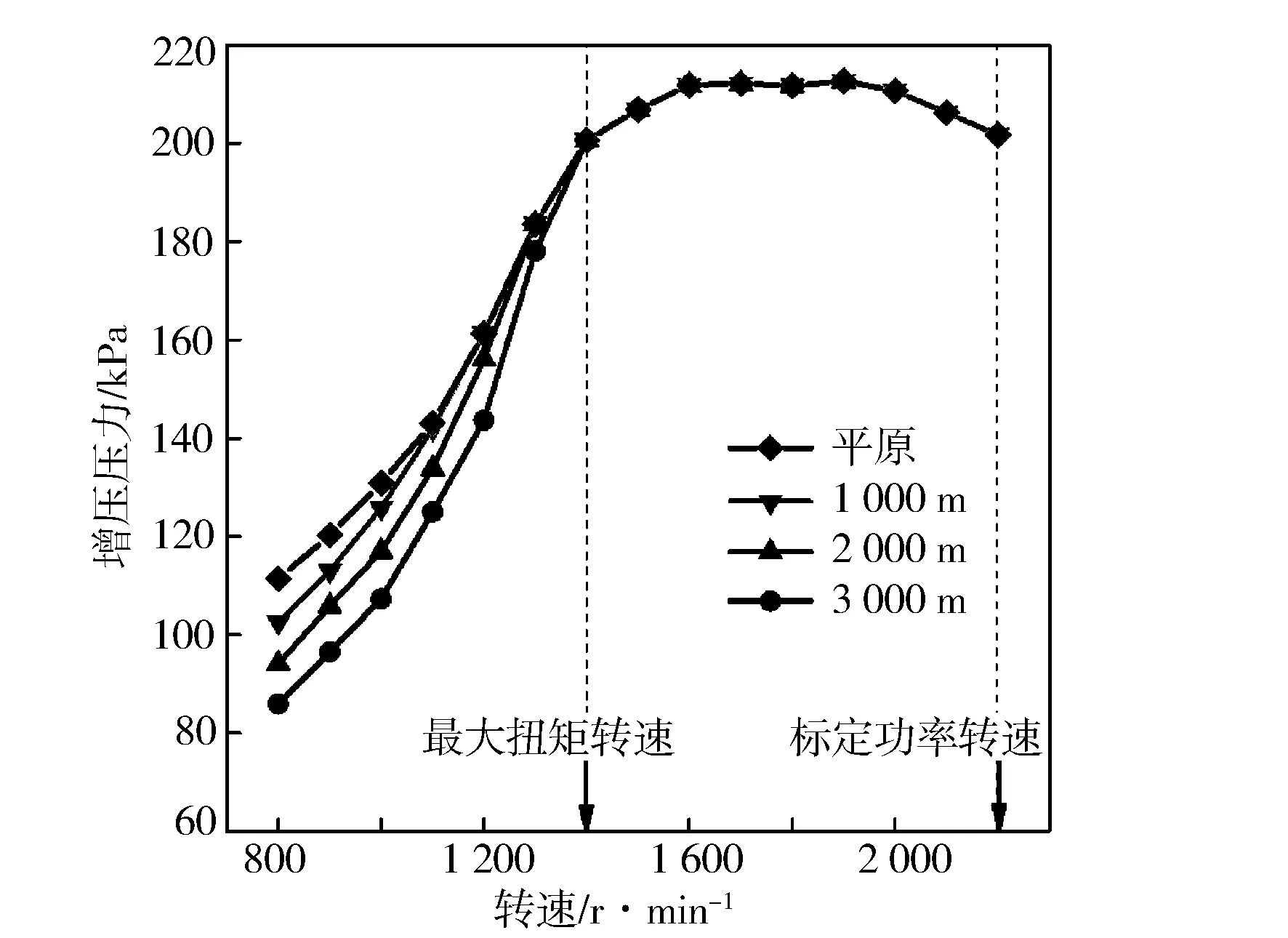
图12 0~3 000 m增压压力恢复情况
3 结束语
本研究在双喷嘴涡轮模型的基础上进行优化,根据动叶喷嘴绝热膨胀的假设以及反动度的计算确定静叶喷嘴出口压力,得出动、静叶膨胀比分配,最终计算涡轮等效流通面积。
经GT-Power仿真验证,此模型反算得到的柴油机性能参数与试验值误差低于4%;计算得到的涡轮特性拟合曲线也与实测曲线接近,误差低于9%,而简单喷嘴模型误差在膨胀比大于2.1时高于15%;并且此模型在膨胀比大于2.2时,未出现涡轮阻塞现象,适用范围比简单喷嘴模型更广。证明此模型能准确描述涡轮的流通特性和工作过程。
结合变海拔等效面积关系式,利用此模型计算得到某柴油机变海拔涡轮等效面积需求,经验证可实现3 000 m最大扭矩点转速到标定功率转速范围内增压压力恢复。证明此模型能准确描述涡轮做功能力,对涡轮增压系统与发动机的匹配有重要意义。
参考文献:
[1] Deutschmann H,张书良.新的增压技术改进了高增压柴油机的性能[J].车用发动机,1987(5):22-36.
[2] 芮鹏.高强化柴油机性能优化及可调涡轮增压系统匹配的仿真研究[D].北京:北京理工大学,2006.
[3] 谢磊,张扬军,诸葛伟林,等.两级增压涡轮几何参数对发动机性能的影响研究[J].车用发动机,2011(6):33-37.
[4] Watson N,Janota S.Turbocharging the Internal Combustion Engine[M].London:McMillan Publishers Ltd,1982.
[5] Li H,Zhang G,Zhang H,et al.Equivalent Matching Model of a Regulated Two-Stage Turbocharging System for the Plateau Adaptability[J].Proceedings of the Institution of Mechanical Engineers Part D Journal of Automobile Engineering,2016(12):230.
[6] Winterbone D E.The Theory of Wave Action Approaches Applied to Reciprocating Engines[M].Netherlands:Springer,1990:445-500.
[7] Payri F,Benajes J,Jullien J,et al.Non-Steady Flow Behavior of Supercharger Turbine[C]//Proceedings of the Third EAEC International Conference.Strasbourg:Springer,1991:347-351.
[8] Payri F,Benajes J,Reyes M.Modelling of Supercharger Turbines in Internal-Combustion Engines[J].International Journal of Mechanical Sciences,1996,38(8):853-869.
[9] Eriksson L.Modeling and Control of Turbocharged SI and DI Engines[J].Oil&Gas Science and Technology,2007,62(4):523-538.
[10] 顾宏中.涡轮增压柴油机性能研究[M].上海:上海交通大学出版社,1998:13.
[11] 梁辰,崔毅,陶一凯,等.车用增压柴油机全工况燃烧放热规律分析[J].内燃机工程,2014,35(5):95-99,106.
[12] 李世伟.柴油机缸内工作过程传热模型的研究[D].济南:山东大学,2012.
[13] 李华雷,石磊,邓康耀,等.D6114柴油机高海拔功率恢复计算研究[J].车用发动机,2013(4):30-35.
[14] Li H,Shi L,Deng K.Research on the Power Recovery of Diesel Engines with Regulated Two-Stage Turbocharging System at Different Altitudes[J].International Journal of Rotating Machinery,2014(3):1-10.
[15] 李华雷,石磊,邓康耀,等.两级可调增压系统变海拔适应性研究[J].内燃机工程,2015,36(3):1-5.

