基于物流时效需求差异的电商平台市场均衡研究
夏德建 王勇


内容提要:随着越来越多的企业和个人将网络市场作为商品销售和采购的重要渠道,网购交易量的节节攀升既促进了电商平台市场的繁荣,也对物流畅通带来了巨大压力。限时物流成为提升物流企业核心竞争力的关键,相关研究也将配送时效作为提升服务和成本控制的约束变量。鉴此,本文将物流时效作为影响买家网购和物流商成本的决定性变量,构建基于线性与非线性物流时效需求的电商平台市场决策模型,求解比较平台、电商、买家和物流商等参与方的决策与收益均衡。研究发现:当买家的网购基本需求越强时,买家的物流时效需求越可能呈现为线性结构,此时线性情景下的平台、电商及物流商的定价水平更低,买家的购买量更大,各方的均衡收益均比非线性情形更高;当买家的网购基本需求偏弱时,买家的物流时效需求越可能表现为非线性结构,此时非线性情景下的平台、电商及物流商的定价水平更低,买家的购买量更大,各方的均衡收益比线性情形下更高。上述结论可为平台、电商及物流商识别买家的需求类型和自身定价决策的合理性,优化其利润空间提供一定的参考。
关键词:网购;物流时效;线性需求;非线性需求;电商平台;博弈;均衡
中图分类号:F2732 文献标识码:A 文章编号:1001-148X(2018)03-0171-06
收稿日期:2017-11-20
作者简介:夏德建(1984-),男,重庆永川人,重庆大学经济与工商管理學院博士研究生,研究方向:物流与供应链管理、双边市场;王勇(1957-),男,四川内江人,重庆大学经济与工商管理学院教授,管理学博士,研究方向:物流优化、双边市场。
基金项目:国家自然科学基金项目“‘电商-平台-物流价值链的决策方法研究”,项目编号:71672015;中央高校基本科研业务费专项项目“电商平台与电商物流的发展模式及竞争策略研究”,项目编号:2017CDJSK02PT09。
随着物流业竞争的加剧,限时物流服务成为提升物流企业核心竞争力的关键所在[1]。各大电商平台、电商企业通过自建物流公司来加快配送,相关的研究也将配送时效作为服务水平和成本控制的重要约束变量[2-3],针对客户等待时间与其满意度负相关的“交货时间窗”研究日渐成为焦点[4-5]。为了表征客户等待时间与其需求的关系,本文将物流配送时间引入网购买家的需求函数之中,并将需求假设为物流时间的减函数,即物流等待时间越长,买家对线上商品的需求越少;考虑到需求与客户等待时间的关系研究尚未有定论,对二者的关系同时考虑了线性与非线性两种减函数形式,希望通过比较上述两种物流时效需求函数影响下的各方决策均衡及收益差异,发现买家的网购基本需求与平台、电商和物流商定价水平的大致关系,旨在为各关联商充分挖掘买家的潜在需求、采取有针对性的策略提供参考。
一、关于研究模型的基本说明
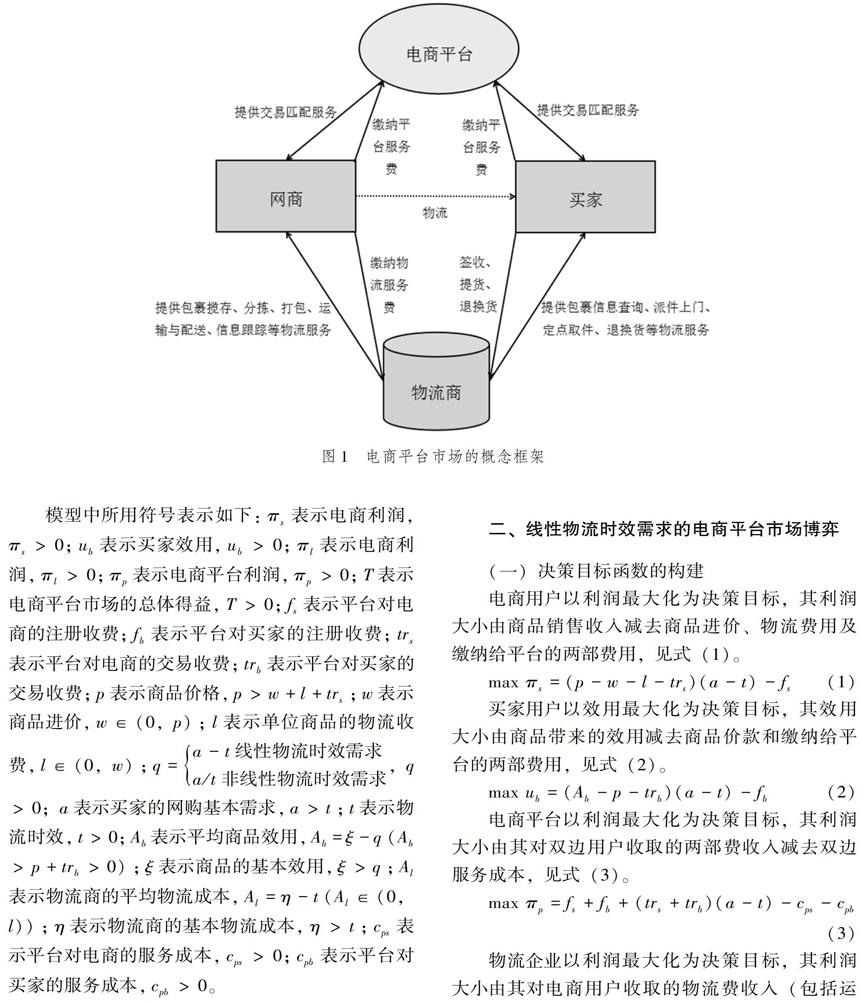
电商平台市场是指由电商平台、电商、买家和物流商等市场参与方在平台主导下进行的由网络平台商品交易、平台中介服务、物流辅助服务等子市场构成的平台经济市场。其中,电商平台企业是核心,负责搭建网络交易平台,是网络商品交易的撮合方。入驻平台的电商是平台的双边用户之一,是电商平台市场的商品销售方。入驻平台的买家是平台的另一侧用户,是电商平台市场的商品购买方。物流企业为双边用户交易的商品提供仓配、流通加工、信息跟踪与查询、派揽件、处理退换货等物流服务,是创造商品时间效用、空间效用和形质效用的物质支撑方。
电商平台市场的框架结构如图1所示,本文将物流时效引入电商平台市场各方的决策博弈模型,假定电商平台对双边用户都收取两部费用,而不对物流商收费,同时考虑电商包邮,分别构建基于线性与非线性两种物流时效需求函数的电商平台市场决策博弈模型。买家需求在两种物流时效需求函数中均为物流时间的减函数,即物流等待时间越长,买家的购买量越少,但相对于物流时间的需求变化速率不同。此外,在两种需求模型中,储运单位商品给物流商带来的平均物流成本也被假定为物流时间的线性减函数,单位商品带给买家的平均效用被假设为买家需求量的线性减函数(即商品的边际效用递减)。电商平台市场各方的决策博弈遵循以下时序:(1)平台确定对双边用户的交易收费(注册收费外生);(2)物流商确定对电商的单位商品物流收费;(3)电商决定商品的售卖价格;(4)买家决定商品的购买数量。按逆向归纳法的操作原理,电商平台市场各方的子博弈精练纳什均衡的求解顺序与决策顺序相反。
图1 电商平台市场的概念框架
模型中所用符号表示如下: π s 表示电商利润, π s>0 ; u b 表示买家效用, u b>0 ; π l 表示电商利润, π l>0 ; π p 表示电商平台利润, π p>0 ; T 表示电商平台市场的总体得益, T>0 ; f s 表示平台对电商的注册收费; f b 表示平台对买家的注册收费; tr s 表示平台对电商的交易收费; tr b 表示平台对买家的交易收费; p 表示商品价格, p>w+l+tr s ; w 表示商品进价, w∈(0,p) ; l 表示单位商品的物流收费, l∈(0,w) ; q=a-t线性物流时效需求
a/t非线性物流时效需求,q>0;a 表示买家的网购基本需求, a>t ; t 表示物流时效, t>0 ; A b 表示平均商品效用, A b=ξ-q (A b>p+tr b>0) ; ξ 表示商品的基本效用, ξ>q ; A l 表示物流商的平均物流成本, A l=η-t (A l∈(0,l)) ; η 表示物流商的基本物流成本, η>t ; c ps 表示平台对电商的服务成本, c ps>0 ; c pb 表示平台对买家的服务成本, c pb>0 。
二、线性物流时效需求的电商平台市场博弈
(一)决策目标函数的构建
电商用户以利润最大化为决策目标,其利润大小由商品销售收入减去商品进价、物流费用及缴纳给平台的两部费用,见式(1)。
max π s=(p-w-l-tr s)(a-t)-f s (1)
买家用户以效用最大化为决策目标,其效用大小由商品带来的效用减去商品价款和缴纳给平台的两部费用,见式(2)。
max u b=(A b-p-tr b)(a-t)-f b (2)
电商平台以利润最大化为决策目标,其利润大小由其对双边用户收取的两部费收入减去双边服务成本,见式(3)。
max π p=f s+f b+(tr s+tr b)(a-t)-c ps-c pb (3)
物流企业以利润最大化为决策目标,其利润大小由其对电商用户收取的物流费收入(包括运输费、仓配费、流通加工费等)减去物流服务成本,见式(4)。
max π l=(l-A l)(a-t) (4)
(二)决策均衡及得益的求解
1.买家的最优决策
将 A b=ξ-q 代入式(2),并对式(2)求 q 的偏导数,得 u b/q=ξ-p-tr b-2q 。令 u b/q=0 ,得:
q=(ξ-p-tr b)/2 (5)
因为 2u b/q2=-2 ,所以式(5)是买家效用最大的购买量。
2.电商的最优决策
将式(5)代入式(1),得 π s=(p-w-l-tr s)(ξ-p-tr b)/2-f s 。对 π s 求 p 的导数,得 π s/p=(ξ+w+l+tr s-tr b)/2-p 。令 π s/p=0 ,得:
p=(ξ+w+l+tr s-tr b)/2 (6)
因为 2π s/p2=-1 ,所以式(6)是使电商利润最优的售价。将式(6)代入式(5),得:
q=(ξ-w-l-tr s-tr b)/4 (7)
3.物流商的最优决策
将式(7)、 t=a-q 和 A l=η-t 代入式(4),得 π l=(4a+w+5l+tr s+tr b-ξ-4η)(ξ-w-l-tr s-tr b)/16 。对 π l 求关于 l 的导数,得 π l/l= (3ξ+2η-3w-5l-3tr s-3tr b-2a)/8 。令 π l/l=0 ,得:
l=(3ξ+2η-3w-3tr s-3tr b-2a)/5 (8)
因为 2π l/l2=-5/8 ,所以式(8)是使物流商利润最优的定价。将式(8)代入式(6)和式(7),可分别得到:
p=(4ξ+w+η+tr s-4tr b-a)/5 (9)
q=(a+ξ-w-η-tr s-tr b)/10 (10)
4.平台的最优决策
将式(10)代入式(3)的平台利润函数中,得 π p=f s+f b+(tr s+tr b)(a+ξ-w-η-tr s-tr b)/10-c ps-c pb 。对 π p 求 tr s 的导数,得 π p/tr s=(a+ξ- w-η-2tr s-2tr b)/10 。令 π p/tr s=0, 得 tr s=(a+ξ-w-η)/2-tr b 。由对称性,同理可得 tr b=(a+ξ-w-η)/2-tr s 。因为 2π p/tr s2=-1/5 , 2π p/tr b2=-1/5 ,所以上述 tr s 和 tr b 是平台对电商和买家的最优交易收费。因此,平台对电商和买家的最优交易收费定价分别为:
tr* s=(a+ξ-w-η)/2-tr* b (11)
tr* b=(a+ξ-w-η)/2-tr* s (12)
5.决策均衡与得益
将式(11)-式(12)代入式(8)-式(10),可得各方的决策均衡,见表1。由表1可知平台对双边用户的最优交易收费定价与买家的基本需求、商品的基本效用正相关,而与电商的商品购进价、物流商的基本物流成本及平台对另一侧用户的交易收费水平负相关;电商的最优商品定价与商品的基本效用、商品进价、物流商的平均物流成本及平台对电商的交易收费正相关,而与买家的基本需求和平台对买家的交易收费负相关;物流商对双边用户交易商品的最优单位物流收费定价与商品的基本效用、物流商的平均物流成本正相关,而与电商的商品进价和买家的基本需求负相关;买家的最优购买量与买家的基本需求、商品的基本效用正相关,而与电商的商品购进价、物流商的基本物流成本负相关。
表1 线性物流时效需求情形的各方决策均衡
决策方决策均衡
平台
tr* s=(a+ξ-w-η)/2-tr* b , tr* b=(a+ξ-w-η)/2-tr* s
电商
p*=(2ξ+3w+3η-3a)/5+tr* s 或 p*=(9ξ+w+η-a)/10-tr* b
物流商 l*=(3ξ+7η-3w-7a)/10
買家 q*=(a+ξ-w-η)/20
将上述决策均衡代入各方的目标函数,可得各方的最优得益,见表2。由表2可知平台、电商、物流商和买家的最优得益水平均与买家的基本需求、商品的基本效用正相关,与电商的商品购进价、物流商的基本物流成本负相关,即电商平台市场各方的均衡得益随买家的基本需求和商品的基本效用的增加而增加,随电商的商品购进价和物流商的基本物流成本的增加而减少。因此,提高网购商品的质量和买家的网购偏好,降低电商的商品进货成本和物流商的基本物流成本应是增加电商平台市场各参与主体得益水平的着力方向。
表2线性物流时效需求情形的各方最优得益
决策方最优得益
平台 π* p=(a+ξ-w-η)2/40+f s+f b-c ps-c pb
电商 π* s=(a+ξ-w-η)2/200-f s
物流商 π* l=(a+ξ-w-η)2/80
买家 u* b=(a+ξ-w-η)2/400-f b
三、非线性物流时效需求的电商平台市场博弈
(一)决策目标函数的构建
非线性物流时效需求情形与线性情形的电商平台市场博弈模型类似,与线性博弈模型的主要差异在于物流时效对买家的需求影响是非线性的。因此,各方决策目标函数构成的博弈模型如式(13)所示。
max π s=a(p-w-l-tr s)/t-f s
max u b=a(A b-p-tr b)/t-f b
max π p=f s+f b+a(tr s+tr b)/t-c ps-c pb
max π l=a(l-A l)/t (13)
(二)决策均衡及得益的求解
求解同线性情形可得非线性物流时效需求情形下各方的最优决策均衡,见表3。将上述决策均衡代入各方的目标函数可得各方的最优得益,见表4。
表3非线性物流时效需求情形的各方决策均衡
决策方决策均衡
平台
tr*′ s=(ξ-w-η)/2-tr*′ b , tr*′ b=(ξ-w-η)/2-tr*′ s
电商
p*′=(3ξ+5w+5η)/8+tr*′ s 或 p*′=(7ξ+w+η)/8-tr*′ b
物流商 l*′=(ξ+3η-w)/4
买家 q*′=(ξ-w-η)/16
表4非线性物流时效需求情形的各方最优得益
决策方最优得益
平台 π*′ p=(ξ-w-η)2/32+f s+f b-c ps-c pb
电商 π*′ s=(ξ-w-η)2/128-f s
物流商 π*′ l=(ξ-w-η)2/64+a
买家 u*′ b=(ξ-w-η)2/256-f b
四、两种物流时效需求博弈均衡的比较
(一)电商平台市场的决策均衡比较
比较线性与非线性物流时效需求下电商平台市场的博弈均衡可得各方的决策均衡差异,见表5。
因为 0<t<η<l<w<p<ξ , p-w-l>0 ,所以 ξ-w-l>0 , ξ-w-η>0 。
令 X=tr* s-tr*′ s , Y=tr*′ b-tr* b , Z=ξ-w-η。 相对线性物流时效需求而言,在非线性物流时效需求下,由表5可知平台既可同时对电商和买家收取更高或更低的交易费用,也可对某边用户收取更高交易费而对另侧用户收取较低交易费,还可对某边用户收取不变交易费而对另侧用户收取更低交易费。总体来说,当 a>2Y(tr*′ b<tr* b) , a>0(tr*′ b>tr* b) 或 a>2X(tr*′ s<tr* s) , a>0(tr*′ s>tr* s) ,即買家的基本需求足够大时,有 tr* s>tr*′ s , tr* b>tr*′ b ,即平台在非线性情形下对双边用户的交易收费均更低;反之,平台在线性情形下对双边用户的交易收费更低。电商对商品的定价方面,非线性物流时效需求情形下的商品价格可高于、低于和等于线性情形。总体来说,当 a<10(X-Y)/7+Z/14 ,即买家的基本需求偏小时,有 p*>p*′ ,即电商在非线性情形下的商品定价更低;反之,电商在线性情形下的商品定价更低。关于两情形下的物流商利润大小,当 0<a<Z/14 ,即买家的基本需求偏小时,有 l*>l*′ ,即非线性情形下的物流商收费更低;反之,物流商在线性情形下的物流收费更低。至于两情形下的买家购买量大小,当 0<a<Z/4 ,即买家的基本需求偏小时,有 q*<q*′ ,即买家在非线性情形下的购买量更大;反之,买家在线性情形下的购买量更大。
表5两种物流时效需求的各方决策均衡比较
决策方决策均衡差异
平台
tr* s-tr*′ s=a/2+tr*′ b-tr* b , tr* b-tr*′ b=a/2+tr*′ s-tr* s
电商
p*-p*′=(ξ-w-η-14a)/40+(tr* s+tr*′ b-tr*′ s-tr* b)/2
物流商 l*-l*′=(ξ-w-η-14a)/20
买家 q*-q*′=[4a-(ξ-w-η)]/80
相对于商品进价 w 、商品的基本效用 ξ 和物流商的基本物流成本 η 等参数,在两种物流时效需求情景下,当买家的基本需求 a 分别大到一定程度时,线性需求情形的平台对双边用户的交易收费定价、电商的商品定价及物流商的物流收费定价均更低,而买家购买量更高;反之,当买家的基本需求 a 偏小时,则非线性需求情形的平台对双边用户的交易收费定价、电商商品定价及物流商收费定价均更低,买家购买量更高。
(二)电商平台市场的最优得益比较
比较线性与非线性物流时效需求下的电商平台市场的博弈均衡得益,可得到各决策主体及总体的最优得益差异,见表6。
由 Z=ξ-w-η , a>0 ,知 2a+(2+5)Z>0 , 4a+9Z>0 ,而 2a+(2-5)Z 和 4a-Z 与零值的大小需要根据各决策方及总体的均衡差异值的临界点分情况讨论。通过比较可得到两情形下各方及总体最优得益的大小关系,如表7所示。
表6两种物流时效需求的各方及总体最优得益差异
决策方最优得益差异
平台 π* p-π*′ p=[2a+(2+5)(ξ-w-η)][2a+(2-5)(ξ-w-η)]/160
电商 π* s-π*′ s=[4a+9(ξ-w-η)][4a-(ξ-w-η)]/3200
物流商 π* l-π*′ l=[2a+(2+5)(ξ-w-η)][2a+(2-5)(ξ-w-η)]/320-a
买家 u* b-u*′ b=[4a+9(ξ-w-η)][4a-(ξ-w-η)]/6400
总体
T*-T*′=3[2a+(2+5)(ξ-w-η)][2a+(2-5)(ξ-w-η)]/320-a+3[4a+9(ξ-w-η)][4a-(ξ-w-η)]/6400
表7两种物流时效需求的各方及总体最优得益比较
决策方 a 的取值最优得益比较
平台 0<a<(5/2-1)Z π* p<π*′ p
a=(5/2-1)Z π* p=π*′ p
a>(5/2-1)Z π* p>π*′ p
电商 0<a<Z/4 π* s<π*′ s
a=Z/4 π* s=π*′ s
a>Z/4 π* s>π*′ s
物流商 0<a<[80-2Z+(80-2Z)2+Z2]/2 π* l<π*′ l
a=[80-2Z+(80-2Z)2+Z2]/2 π* l=π*′ l
a>[80-2Z+(80-2Z)2+Z2]/2 π* l>π*′ l
买家 0<a<Z/4 u* b<u*′ b
a=Z/4 u* b=u*′ b
a>Z/4 u* b>u*′ b
总体 0<a<[800-72Z+(800-72Z)2+1566Z2]/72 T*<T*′
a=[800-72Z+(800-72Z)2+1566Z2]/72 T*=T*′
a>[800-72Z+(800-72Z)2+1566Z2]/72 T*>T*′
表7中 a 在各区间的临界点取值具有以下关系: (5/2-1)Z<Z/4<[800-72Z+(800-72Z)2+1566Z2]/72<[80-2Z+(80-2Z)2+Z2]/2 。相对于线性物流时效需求而言,当 0<a<(5/2-1)Z 时,非线性情形下的平台、电商、物流商的利润水平和买家效用、总体福利水平均更高;当 (5/2-1)Z<a<Z/4 时,非线性情形下的电商和物流商的利润水平、买家效用及总体福利水平都更高,但非线性情形下的平台利潤水平却更低;当 Z/4<a<[80-2Z+(80-2Z)2+Z2]/2 时,非线性情形下的物流商利润和总体福利水平更高,但非线性情形下的平台、电商的利润水平和买家效用均更低;当 [800-72Z+(800-72Z)2+1566Z2]/72<a<[80-2Z+(80-2Z)2+Z2]/2 时,物流商和总体福利在非线性情形下更高,而平台、电商的利润及买家效用均没有线性情形高;当 a>[80-2Z+(80-2Z)2+Z2]/2 时,电商平台市场各参与方及市场总体福利在线性情景下的得益水平均要高于非线性情形。
相对于商品进价 w 、商品的基本效用 ξ 和物流商的基本物流成本 η 等参数,在两种物流时效需求情景下,当买家的基本需求 a 分别大到一定程度时,线性需求情景的各方得益与总体福利水平均比非线性物流时效需求情形更高,即当买家的基本需求偏大时,线性需求下的买家效用水平更高,同时也使得平台、电商和物流商的利润水平更高,这说明买家的购买能力和对商品的整体偏好越强,其网购的物流时效需求越趋近于线性需求;反之,当 a 偏小时,则非线性需求情景的各方得益与总体福利水平均更高,即当买家的基本需求偏小时,非线性需求下的买家效用水平和平台、电商、物流商的利润水平更高,这说明买家的购买能力和对商品的整体偏好越弱,其网购的物流时效需求更可能为非线性需求。
五、结束语
本文将物流时效假设为决定买家网购需求和物流商运营成本的决定性因素,从电商平台对双边用户收取两部费用视角,分析了关于物流时效的线性与非线性需求差异带来的各方决策均衡与得益水平影响,并得出如下结论:当买家的网购基本需求强度偏强,即买家对网络购物的偏好程度上升至某较高水平时,在线性物流时效需求情景下,平台对双边用户的最优交易收费定价、电商的最优商品定价和物流商的最优物流收费定价水平均要比非线性需求情景低,而买家的最优购买量比非线性情景更大,且电商平台市场各方及总体的均衡收益水平均比非线性情形更高。因此,当买家具有更高的网络购物需求时,买家的物流时效需求函数往往表现为线性结构形式。反之,当买家的购买力偏弱,网购渠道给买家带来的效用水平低至某一程度时,非线性物流时效需求情景下的平台对双边用户的最优交易收费定价、电商的最优商品定价和物流商的最优物流收费定价水平均要比线性需求情景低,而买家的最优购买量在非线性情景更大,且非线性情景下的电商平台市场各方及总体的均衡收益水平均比线性情景更高,可知买家在具有较弱的网购基本需求强度下的物流时效需求函数越可能表现为非线性结构形式。所以,电商平台市场上各方的博弈均衡一定程度上具有暴露买家物流时效需求类型的功能,使得平台、电商及物流商等企业可迅速根据买家的交易表现掌握买家的需求特点,同时结合关联商的定价行为甄别自身决策的合理性,适时调整定价策略,以便最大化实现决策目标。
參考文献:
[1] 冯雄华.物流限时服务特点与操作分析[J].中外物流,2007(6):37-40.
[2] 史伟.考虑时效约束的物流系统选址研究[J].云南民族大学学报(自然科学版),2009(1):89-91.
[3] 张跃,尹春华.基于AHP-SPC的项目物流配送时效监控体系[J].物流工程与管理,2015(10):51-53+73.
[4] Mcnabb M E, Weir J D, Hill R R, et al.Testing local search move operators on the vehicle routing problem with split deliveries and time windows[J].Computers and Operations Research,2015,56(6):93-109.
[5] 黄益平,杨琴,李青,等.考虑客户等待时间感知的快递车辆优化调度[J].工业工程,2017,20(4):31-36+48.
Research on Game Equilibrium of E-commerce Platform Market Influenced by
Demand Discrepancy based on Logistics Timeliness
XIA De-jian1,2, WANG Yong1,2
(1. School of Economics and Business Administration, Chongqing University, Chongqing
400044,China; 2.Key Laboratory of Modern Logistics of Chongqing, Chongqing University,
Chongqing 400044, China)
Abstract:With the popularity of internet transactions, more and more enterprises and individuals have taken the internet market as an important channel for product purchase and sale. The increase in the volume of online shopping has not only promoted the prosperity of the e-commerce platform market, but also brought great pressure to the smooth logistics. Logistics timeliness is considered as the decisive variable affecting buyer′s online shopping and logistics costs. The paper constructs two different decision-making game models of the e-commerce platform market based on the buyer′s demand function affected by linear and non-linear logistics timeliness, solving and comparing the equilibrium of the decisions and income of the participants of the e-commerce platform market, such as e-commerce platform company, the online seller, the online buyer and the logistics express enterprise. The results show that the stronger the basic demand of buyer′s online shopping, the more likely the buyer′s demand function for logistics timeliness is linear, so under this circumstance, the prices of the platform, the online seller and the logistics provider are lower, while the buyer′s purchase quantity is higher, and the equilibrium returns of all parties are higher than those of nonlinear scenarios;on the contrary, when the buyer′s basic demand for online shopping is weaker, the more likely the buyer′s demand function for logistics timeliness is nonlinear, so under this circumstance, the prices of the platform, the online seller and the logistics provider are lower, while the buyer′s purchase quantity is higher, and the equilibrium returns of all parties are higher than those of linear scenarios. The decision equilibrium of the two different kinds of demand function can provide some reference for the platform, the online seller and the logistics express enterprise to quickly identify the buyer′s demand type and realize the rationality of their price decisions, and then optimize their profit margins.
Key words:online shopping; logistics timeliness; linear demand; nonlinear demand; e-commerce platform; game; equilibrium

