三次B-样条配点法定价欧式看跌期权

吴蓓蓓

(1. 同济大学 数学科学学院， 上海 200092； 2. 上海电力学院 数理学院， 上海 200090)

期权，又称选择权，它赋予其持有者在一个特定的时间或之前以预先指定的价格买入或卖出标的资产的权利.期权价格是期权合约中唯一随市场供求变化而改变的变量，它的高低直接影响到买卖双方的盈亏状况，是期权交易的核心问题.

对Black-Scholes模型[1]及其推广形式进行期权定价时，很难找到解析解.虽然欧式期权的解析解存在，但是复杂的定价表达式往往给计算带来许多困难，因此人们更愿意采用高效的数值方法研究期权定价问题.常用的数值方法主要有：格点法、二叉树法、Monte Carlo方法、有限差分法、有限体积法等[2-9].

B-样条的概念最初是由Schoenberg[10]于20世纪40年代中期提出来的，如今已得到很大的发展.B-样条具有几何不变性、凸包性、保凸性、变差减小性、局部支撑性等许多优良性质.B-样条配点法构造简单，数值精度高，易处理复杂的边界问题，目前已成为求解偏微分方程的重要数值方法之一.

近年来，B-样条配点法也被众多学者应用于期权定价问题的计算中，并受到了广泛的关注和研究[11-15].本文重点研究Black-Scholes模型下欧式看跌期权定价的数值解.将三次B-样条的基函数重新定义，对Black-Scholes方程空间离散采用改进的三次B-样条配点法，时间离散采用向前有限差分，并引入参数θ，建立混合差分格式.利用稳定性分析的Von Neumann条件，证明了该格式当1/2≤θ≤1时是无条件稳定的.数值实验表明，本文改进的三次B-样条配点法对求解欧式看跌期权定价问题是有效的，提高了逼近精度，减少了CPU时间，且其Crank-Nicolson格式的数值结果要优于隐式欧拉格式.

1 欧式看跌期权模型

考虑定义在区域Σ:{0≤S<,0≤t≤T}上的Black-Scholes方程：

(1)

终止条件为

f(S,T)=max(E-S,0),

(2)

其中,f(S,t)是欧式看跌期权价格，它随着原生资产价格S和时间t的变化而变化,σ和r分别为波动率和无风险利率(均假定为常数),T为到期日，E为执行价格.

为了利用数值方法求解，把问题限制在一个有限区域

[Smin,Smax]×[0,T]，

其中Smin和Smax为适当选取的非负数.

补充边界条件：

f(Smin,t)=α(t),f(Smax,t)=β(t),
t∈[0,T].

(3)

作变换S=ex，即x=lnS，则上述问题可转化为求下列定解问题

(4)

它的边界条件为

u(xmin,t)=α(t),u(xmax,t)=β(t),

(5)

其中,u(x,t)=f(S,t)，(x,t)∈[xmin,xmax]×[0,T]，

xmin=lnSmin，xmax=lnSmax.

2 B-样条配点法

以空间步长h和时间步长τ将求解区域

[xmin,xmax]×[0,T]

划分为均匀网格，网格点为(xj,tk),其中,

利用三次B-样条基函数配点法可将方程(4)的逼近解表示成

(6)

其中,cj(t)是与时间t相关的未知量，Bj(x)是三次B-样条基函数[16]，定义为

(7)

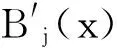
表 1 函数Bj(x)及其导数在节点处的值

记(xj,t)处的逼近解为Uj=U(xj,t)，根据表1，逼近解Uj及其关于x的一阶和两阶导数分别为

Uj=cj-1+4cj+cj+1,

(8)

U(x0,t)=c-1+4c0+c1=α(t),

U(xN,t)=cN-1+4cN+cN+1=β(t).

(9)

从逼近(6)和(9)式中消除c-1和cN+1，重新定义B-样条的基函数，将逼近解写成下列形式

(10)

其中

(11)

且

(12)

在点(xj,tk)处取关于时间变量的一阶向前差商，并引入参数θ(0≤θ≤1)，(4)式中的偏微分方程可以离散化为

(13)

当θ=0时，(13)式为差分显式格式；当θ=1/2时，(13)式为Crank-Nicolson格式；当θ=1时，(13)式为隐式欧拉格式.

校园建设中，对安全的重视不仅体现在对网络设备的投入，而且还体现在对安全维护人员配备上。国内大部分高校，没有专门的编制去配备网络安全人员。网络中心的工作人员只是负责服务器、存储设备的基本维护。导致一旦发生安全问题，心有余而力不足，不能快速处理。

将逼近解(6)式代入(13)式中，并利用(11)、(12)式及表1，可得下面矩阵形式

PCk=QCk+1+b,

(14)

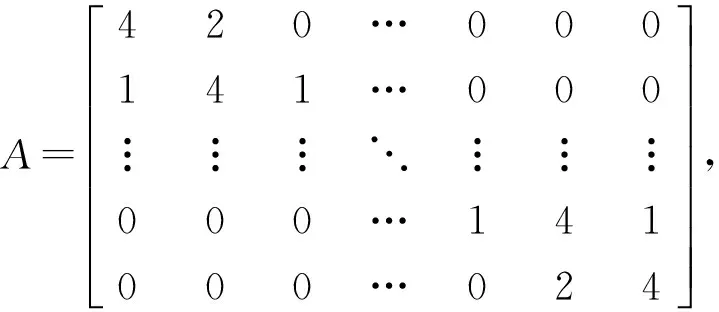
其中，

且

这里P和Q是(N+1)×(N+1)阶三对角矩阵，b是(N+1)阶列向量，由边界条件确定.

(i)Ux(xj,T)=g′(xj),j=0；

(ii)U(xj,T)=g(xj),j=0,1,…,N；

(iii)Ux(xj,T)=g′(xj),j=N.

对应的矩阵形式为

ACM=f,

(15)

其中，

3 稳定性分析

由(14)式，可以得到下列差分方程

(16)

现在采用Fourier分析方法来研究其稳定性所需要满足的条件.

令

(17)

将(17)式代入到(16)式中，化简后，可得增长因子为

(18)

其中,

(19)

根据Von Neumann 条件，要保证(16)式稳定，需满足条件|G(θ)|≤1，即

(20)

其中,

易验证G(θ)在θ=0处取到极大值.在(20)式中令θ=0，于是有

(21)

从而解得

(22)

由此可知，当满足(22)式时，格式(16)是稳定的.这表明，当1/2≤θ≤1时，差分格式(16)是无条件稳定的.

4 数值实验

下面用数值实验来验证有效性.

考虑不支付红利的4月期标的资产为股票的欧式看跌期权，假设敲定价格为12美元，无风险利率为每年5%，波动率为每年25%，用符号记为

T=0.3,E=12,r=0.05,σ=0.25,

且计算区域为[1,21]×[0,0.3]，相应的边界条件为α(t)=Ee-r(T-t)-S,β(t)=0.

数值实验中相对误差的计算公式为

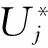
图1显示了当网格剖分为(M,N)=(200,200)时，采用本文三次B-样条配点法 (θ=1/2) 计算该欧式看跌期权所得的(a)期权价格曲面和当t=0时刻的(b)相对误差.从图中不难看出，数值结果是稳定的.

当网格剖分为(M,N)= (120,120)时，选取不同的θ值，对应的相对误差也不同，如图2所示.相对误差走势基本相同，而随着时间t减少，三次B-样条配点法的Crank-Nicolson格式(θ=0.5)的整体误差最小.

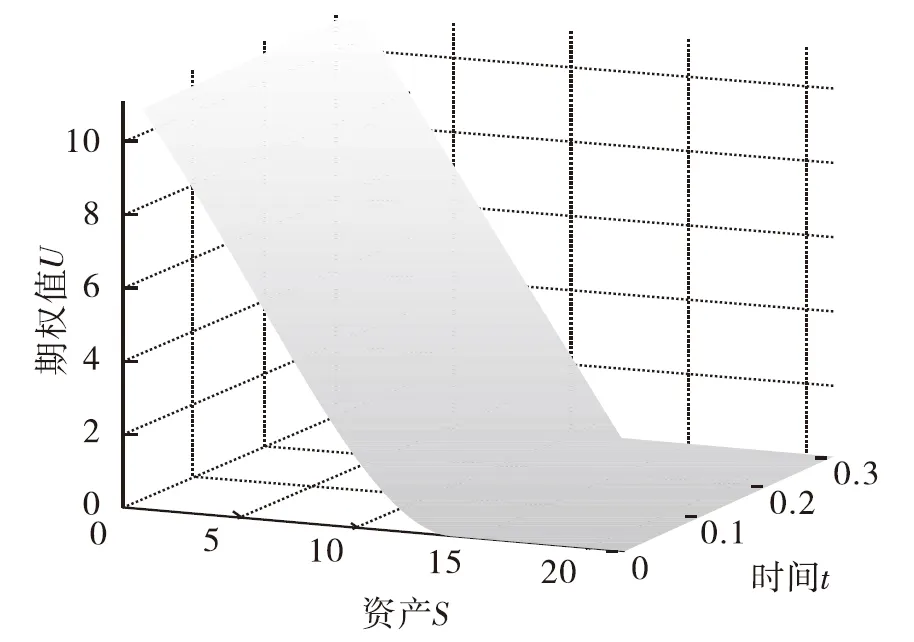
(b) 相对误差

图 2 不同θ值的相对误差比较

将本文Crank-Nicolson格式与文献[12]中差分格式的相对误差和CPU时间作比较，如表2所示.本文的数值方法比文献[12]的三次B-样条配点法略提高了精度，且有效地减少了CPU时间.

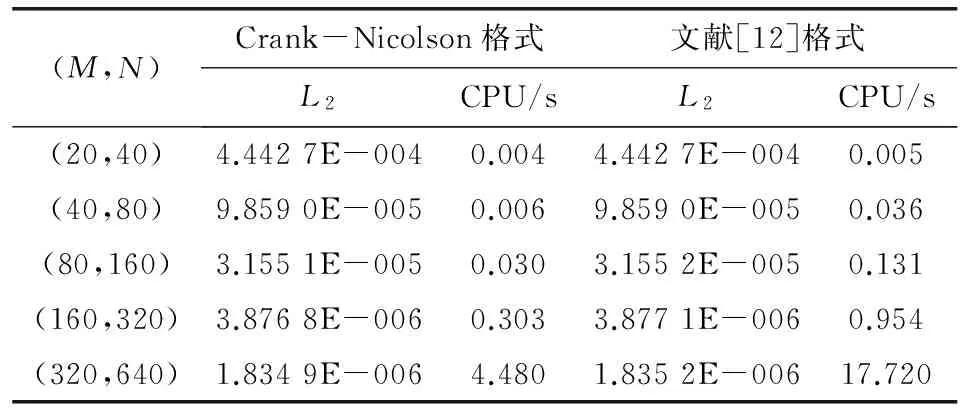
表 2 相对误差和CPU时间比较

5 结束语

本文利用重新定义基函数的三次B-样条配点法定价Black-Scholes模型下的欧式看跌期权.数值实验表明，该方法逼近精度高，求解快捷、简便.此外，其Crank-Nicolson格式的逼近效果要好于隐式欧拉格式.文中所构造的数值方法在期权定价中是有效的.

[1] BLACK F, SCHOLES M. The pricing of options and corporate liabilities[J]. J Polit Econ,1973,81(3):637-659.

[2] COX J C, ROSS S, RUBINSTEIN M. Option pricing:a simplified approach[J]. J Financ Econ,1979,7(3):229-264.

[3] GAUDENZI M, PRESSACCO F. An efficient binomial method for pricing American put options[J]. Decis Econ Financ,2003,26(1):1-17.

[4] LIU Q, GUO S X. Variance-constrained canonical least-squares Monte Carlo:an accurate method for pricing American options[J]. N Am J Econ Financ,2014,28(322):77-89.

[5] CHAWLA M M, EVANS D J. High-accuracy finite-difference methods for the valuation of options[J]. Int J Comput Math,2005,82(9):1157-1165.

[6] FADUGBA S E, NWOZO C R. Crank Nicolson finite difference method for the valuation of options[J]. Pac J Sci Tec,2013,14(2):136-146.

[7] ANGERMANN L, WANG S. Convergence of a fitted finite volume method for the penalized Black-Scholes equation governing European and American option pricing[J]. Numer Math,2007,106(1):1-40.

[8] 甘小艇，殷俊峰. 二次有限体积法定价美式期权[J]. 计算数学,2015,37(1):67-82.

[9] 甘小艇，易华. 有限体积元法定价欧式期权[J]. 四川师范大学学报(自然科学版),2016,39(3):327-331.

[10] SCHOENBERG I J. Contributions to the problem of approximation of equidistant data by analytic functions[J]. Q Appl Math,1946,4:3-57.

[11] KADALBAJOO M K, TRIPATHI L P, KUMAR A. A cubic B-spline collocation method for a numerical solution of the generalized Black-Scholes equation[J]. Math Comp Model,2012,55(3/4):1483-1505.

[12] RASHIDINIA J, JAMALZADEH S, MOHEBIANFAR E. B-spline collocation approach to the solution of options pricing model[J].J Comput Sci Comput Math,2014,4(1):5-9.

[13] SERGHINI A, ElHAJAJI A, MERMRI E B, et al. Pricing of European options using a cubic spline collocation method[J]. Int J Appl Math Stat,2013,47(17):15-28.

[14] HUANG J, CEN Z D. Cubic spline method for a generalized Black-Scholes equation[J]. Math Prob Eng,2014,2014(3):1-7.

[15] MOHAMMADI R. Quintic B-spline collocation approach for solving generalized Black-Scholes equation governing option pricing[J]. Comput Math Appl,2015,69(8):777-797.

[16] MITTALR C, JAINR K. B-splines methods with redefined basis functions for solving fourth order parabolic differential equations[J]. Appl Math Comput,2011,217(23):9741-9755.