高斯整数环的商环的5次幂映射图

2018-04-28 02:32韦扬江梁艺耀唐高华

四川师范大学学报（自然科学版） 2018年2期

韦扬江, 梁艺耀, 唐高华,2*

(1. 广西师范学院数学与统计科学学院, 广西南宁 530023; 2. 钦州学院理学院, 广西钦州 535011)

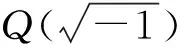
令Z为整数环,Zn为模n整数剩余类环.对于任一正整数n,记模n高斯整数环为Zn[i],即Z[i]/〈n〉≅Zn[i].如果α∈Zn[i],则α=x+yi,这里x与y均为Zn中的元素.定义Zn[i]上的5次幂映射图G(n),该映射图的顶点为Zn[i]中的所有元素,并且,对于图中的2个顶点α和β,如果β=α5,则从α到β有一条有向边,且称α为β的一个母点,而β称为α的衍生点.用indeg(β)表示β的入度,即β的所有母点的个数.如果α的衍生点是它本身,即α5=α,则α称为不动点.如果α为不动点,并且indeg(α)=1,则α称为孤立不动点.

在G(n)中的每一个极大连通部分叫做G(n)的一个连通分支.显然Zn[i]中的单位和零因子不可能位于同一连通分支,所以可以定义G(n)的2个子图G1(n)、G2(n),其中G1(n)是由Zn[i]中所有单位及这些单位之间的有向边组成的子图,G2(n)是由Zn[i]中所有零因子及这些零因子之间的有向边组成的子图.若α是G(n)的顶点,α→α5→α52→…→α5m=α,且对于t∈{0,1,…,m-1},均有α5t≠α,则称由α,α5,α52,…,α5m-1组成的图为圈,且圈长为m.一个连通分支称为孤立圈当且仅当这个连通分支上的点都在圈上.

一个图称为正则的当且仅当存在正整数d,使得图中所有顶点的入度等于d.一个图称为半正则的当且仅当存在正整数d,使得图中所有顶点的入度等于d或者0.显然,正则图也是半正则的.

令R为任意的交换环,定义U(R)为R的单位群,D(R)为R中所有零因子构成的集合.对于α∈U(R),定义o(α)为α在U(R)中的阶.如果R为模n整数环Zn,将α在环Zn中的阶用ordn(α)表示.不失一般性,也用Zn表示n阶循环群.

本文研究了Zn[i]的5次幂映射图G(n)的结构,包括G(n)中不动点的个数,顶点0和1的入度,G(n)的半正则性,将文献[4-5]中的相关结论从3次幂推广到5次幂.

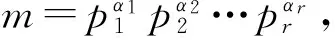
1) 当gcd(m,n)=1时,同余方程xn≡1(modm)的解数为

gcd(n,p1-1)×gcd(n,p2-1)×
…×gcd(n,pr-1).

2) 当x=c0是xn≡a(modm)的一个解时,它的全部解为x≡c0y(modm),这里y是yn≡1(modm)的解.

引理2[9]假设a+bi∈Zn[i],则:

1) 元素a+bi是Zn[i]的单位当且仅当a2+b2是Zn的单位;

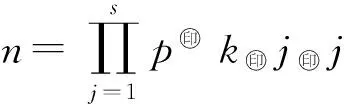
其中

3)Zn[i]是局部环当且仅当n=2t或qt,其中q是素数且q≡3(mod4),t≥1;

4)Zn[i]是域当且仅当n=q,其中q是素数且q≡3(mod4).

引理3[11]1)U(Z2[i])≅Z2,U(Z4[i])≅Z2⊕Z4,U(Z2t[i])≅Z4⊕Z2t-1⊕Z2t-2,t>2.因此|U(Z2t[i])|=22t-1,|D(Z2t[i])|=22t-1.

2) 若q是素数且q≡3(mod4),则U(Zqt[i])≅Zqt-1⊕Zqt-1⊕Zq2-1,t≥1.因此|U(Zqt[i])|=q2t-q2t-2,|D(Zqt[i])|=q2t-2.

3) 若p是素数且p≡1(mod4),则U(Zpe[i])≅Zpe-1⊕Zpe-1⊕Zp-1⊕Zp-1,e≥1.因此

|U(Zpe[i])|=(pe-pe-1)2,
|D(Zpe[i])|=2p2e-1-p2e-2.

与文献[5]中引理2.4类似,可以证得以下引理.

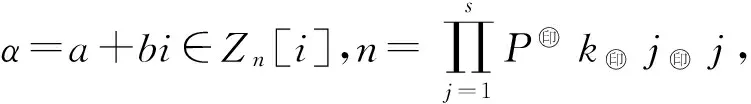
与文献[6]中定理2.7类似可得以下引理.

1 主要结论

如果没有特别说明,均以p表示素数且p≡1(mod4),而以q表示素数且q≡3(mod4).

令α=x+yi∈G(n),则α是G(n)中的不动点当且仅当α5=α,即以下2个同余式成立：

x5-10x3y2+5xy4≡x(modn),

(1)

y5-10x2y3+5x4y≡y(modn).

(2)

下面令

(3)

是整数n的素数分解式,其中,k,m,l≥0,tj,es≥1,qj是素数且qj≡3(mod4),ps是素数且ps≡1(mod4).下面定理给出了G(n)中不动点的个数.

定理6若n的素数分解式为(3)式,则对应的映射图G(n)中不动点的个数L(n)为

证明令α=x+yi∈Zn[i]并且α5=α.由引理4,只需求出n是素数的方幂时G(n)的不动点个数即可.

1) 令n=2k,k=1,2.容易算出L(2)=3,L(22)=9.

接下来,令k≥3.若α是Zn[i]中的零因子,由于α(α4-1)=0,又因为Z2k[i]是局部环,所以α4-1是Z2k[i]中的单位,因此α5=α当且仅当α=0.

若α是Z2k[i]中的单位,则得α4=1,即以下2个同余式成立：

x4-6x2y2+y4≡1(modn),

(4)

4x3y-4xy3≡0(modn).

(5)

因为α是单位,所以x与y的奇偶性互异.

若x是奇数,y是偶数,由于同余式(5)等价于xy(x2-y2)≡0(mod2k-2),又因为x2-y2必是奇数,故由同余式(5)得y≡0(mod2k-2).所以y=2k-2d,这里d=0,1,2,3.进而可以得到,当k≥3时,无论y是上述4个取值的哪一个,都有2k|6y2和2k|y4.所以同余式(4)可化简为x4≡1(mod2k).由于当k≥3时,剩余类环Z2k的单位群U(Z2k)同构于Z2×Z2k-2,故当k=3时在U(Z2k)中恰有4个元素的4次方等于1,而当k>3时在U(Z2k)中恰有8个元素的4次方等于1.因此同余方程x4≡1(mod2k)的解数在k=3时等于4,在k>3时等于8.所以,当2⫮x且2|y时,由同余式(4)和(5)构成的同余方程组在k=3时恰有4×4=16个解,在k>3时恰有4×8=32个解.

当y是奇数,x是偶数时,证明过程与前面类似,此时由同余式(4)和(5)构成的方程组也是在k=3时恰有4×4=16个解,在k>3时恰有4×8=32个解.

所以k=3时,L(2k)=16+16+1=33,当k>3时,L(2k)=32+32+1=65.

2) 令n=qt,t≥1.由引理2,此时Zqt[i]是局部环.若α5=α且α是Zqt[i]中的零因子,则显然α=0.

下面,假设α∈U(Zqt[i])且α5=α,则必有α4=1.如果α=d(1±i),其中d∈{1,…,qt-1}且q⫮d,易得-4d4≡1(modqt),即(2d2)2≡-1(modqt).然而,由文献[14]第196页的推论3可知,当q≡3(mod4)时,同余方程X2≡-1(modq)无解.所以,X2≡-1(modqt)无解.故同余式(2d2)2≡-1(modqt)对任意的d∈{1,…,qt-1}都不成立.所以映射图G(qt)中没有形如α=d(1±i)的不动点.

现在,假设α=x+yi且x≢±y(modqt).由同余式(5)得xy(x2-y2)≡0(modqt).如果q⫮xy,这时有x2≡y2(modqt),这与x≢±y(modqt)矛盾.所以,q必整除x或y.又由引理2的1)知,q不能同时整除x和y.首先,令q|x,q⫮y.由同余式(5)得,x(x2-y2)≡0(modqt).如果qt⫮x,则必有q|(x2-y2).由于q|x,所以可知q|y,这与q⫮y矛盾.因此,必有qt|x即x=0且q⫮y.同理,可得qt|y即y=0且q⫮x.先讨论qt|x且q⫮y的情形.由同余式(4)可得y4≡1(modqt),此同余方程的解数为gcd(4,q-1)(引理1).由于q≡3(mod4),所以gcd(4,q-1)=2.因此当x=0且q⫮y时,由同余式(4)和(5)构成的方程组的解数为2.同理当y=0且q⫮x时,此方程组的解数也为2.因此Zqt[i]的单位群中恰有4个元素为不动点.

所以,L(qt)=4+1=5.

3) 令n=pe,e≥1.根据引理2的3)可知,此时Zpe[i]不是局部环.显然α=0是一个不动点.下面假设α∈D(Zpe[i])且α≠0.由引理2的1),p|(x2+y2).所以p同时整除x与y或者同时不整除x与y.首先,由同余式(1)与(2)可得

如果p同时整除x与y,则p⫮ (x4-10x2y2+5y4-1)且p⫮ (y4-10x2y2+5x4-1),所以由以上2个同余式得pe|x且pe|y,即x=y=0,这与α≠0矛盾.因此可以推出p⫮xy.那么,上述方程组等价于

x4-10x2y2+5y4-1≡0(modpe),

(6)

y4-10x2y2+5x4-1≡0(modpe).

(7)

(6)与(7)式相减可得4x4-4y4≡0(modpe),即pe|(x2+y2)(x2-y2).若p|(x2-y2),则由p|(x2+y2),可得p|x且p|y,与p⫮xy矛盾.所以有p⫮ (x2-y2).从而x2+y2≡0(modpe).将x2≡-y2(modpe)代入(6)式得(2x)4≡1(modpe),此方程的解数等于gcd(4,p-1)(引理1).又因为p≡1(mod4),所以gcd(4,p-1)=4.因为对给定的每个x,关于y的同余方程x2+y2≡0(modpe)都有2个解,所以当p|(x2+y2)且x≠0,y≠0时,由(6)和(7)式构成的方程组的解数为8,即Zpe[i]恰有8个非零的零因子为不动点.

下面,假设α∈U(Zpe[i]).如果α=d(1±i),其中d∈{1,…,pe-1}且p⫮d,由α5=α易得-4d4≡1(modpe),即

(2d2)2≡-1(modpe).

(8)

由于p≡1(mod4),由文献[14]的推论3知,同余方程Y2≡-1(modp)恰有2个解.从而由文献[16]的引理2.3得,方程Y2≡-1(modpe)恰有2个解,记为Y≡Yj(modpe),j=1,2.再由文献[16]的引理2.3知,方程2d2≡Yj(modpe)的解数为2.因此方程(8)的解数为4.所以Zpe[i]的单位群中形如α=d(1±i)的不动点个数为8.

现在,假设α=x+yi且x≢±y(modpe).与本定理情形2)的证明类似,可得x=0且p⫮y,或y=0且p⫮x.对于前者,有y4≡1(modpe),此方程的解数为gcd(4,p-1)=4.因此当x=0且p⫮y时,由同余式(4)和(5)构成的方程组的解数为4.同理当y=0且p⫮x时,由同余式(4)和(5)构成的方程组的解数也为4.从而Zpe[i]的单位群中形如α=x+yi且x≢±y(modpe)的不动点个数为8.

所以L(pe)=1+8+8+8=25.

定理7令

n=2k5

其中k,w,l,m,λ≥0,eh,μs,tj≥1,并且,p1,…,pl是互不相同的素数且ph≡1(mod20),h=1,2,…,l;π1,π2,…,πm是互不相同的素数且πs≡11,19(mod20),s=1,2,…,m;η1,η2,…,ηλ为互不相同的素数且ηj≡3,7,9,13,17(mod20),j=1,2,…,λ,则G(n)中单位元1的入度indeg(1)为:

证明由引理4,只需求出n是一个素数的方幂时G(n)中单位元1的入度.

1) 令n=2k,k≥1.由引理3,对于α∈U(Z2k[i]),都有5⫮o(α).因此,根据文献[15]的定理2.5得,对于α∈U(Z2k[i]),α都在G(2k)的圈上.所以,indeg(1)=1.

2) 令n=5w,若w=1,由引理3可知,5⫮o(α),这里α∈U(Z5[i]).因此,根据文献[15]中的定理2.5得,indeg(1)=1.若w≥2,由引理3,U(Z5w[i])中满足α5=1的元素个数为52.所以当w≥2时,G(5w)中单位元1的入度indeg(1)=52.

3) 令n=pe,e≥1,p是模4余1的素数且p≠5.由引理3,U(Zpe[i])≅Zpe-1⊕Zpe-1⊕Zp-1⊕Zp-1.显然5⫮pe-1.又,若5|(p-1),则由4|(p-1),得20|(p-1),即p≡1(mod20).这时循环群Zp-1中满足α5=1的元素个数为5.因此,当p≡1(mod20)时,G(pe)中单位元1的入度indeg(1)=5×5=52.当p≢1(mod20)即p≡9,13,17(mod20)时,G(pe)中单位元1的入度indeg(1)=1.

证明由引理4,只需求出n是一个素数的方幂时0在G(n)的入度.假设n=pt,p为素数,t≥1.令α=a+bi∈Zpt[i],且α5=0,则显然α为零因子,即p|(a2+b2),且有

a5-10a3b2+5ab4≡0(modpt),

(9)

b5-10a2b3+5a4b≡0(modpt).

(10)

1) 假设n=pt,p为奇素数,t≥1.由p|(a2+b2)得,或者p同时整除a与b,或者p⫮ab.如果p⫮ab,则由同余式(9)有

a4-10a2b2+5b4≡0(modpt).

(11)

由于p|(a2+b2),可令a2=pd-b2,d为整数,代入同余式(11)得

p2d2≡4b2(3pd-4b2)(modpt).

(12)

因为p⫮b,所以p⫮ (3pd-4b2).故同余式(12)不成立.从而,当p⫮ab时,α5≠0.因此,必有p同时整除a与b.令a=pma1,b=pμb1,其中p⫮a1b1,m与μ为正整数.又令s=min{m,μ}.则α=psα1,这里α1=pm-sa1+pμ-sb1i.显然,当s≥「t/5⎤,即当

p「t/5⎤|a,p「t/5⎤|b

(13)

时,同余式(9)和(10)式都成立,从而α5=0.由于0≤a,b≤pt-1,因此满足条件(13)的α共有p2(t-「t/5⎤)个.下面令1≤s≤「t/5⎤-1.

当m=μ=s时,α5=0当且仅当以下2个同余式同时成立:

(14)

(15)

(16)

当m>μ=s时,若α5=0,则由(10)式可得

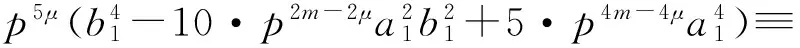
(17)

由于p⫮b1,故

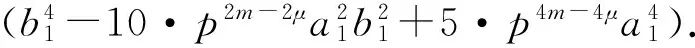
从而同余式(17)成立当且仅当5μ≥t,即μ≥「t/5⎤.但考虑到前提条件是1≤s≤「t/5⎤-1且μ=s,因此同余式(17)不可能成立.所以,当1≤s≤「t/5⎤-1且m>μ=s时,α5≠0.

当1≤s≤「t/5⎤-1且μ>m=s时,同理可证α5≠0.所以α5=0当且仅当α=a+bi满足条件(13).故在G(pt)中,顶点0的入度indeg(0)=p2(t-「t/5⎤).

2) 假设n=pt,p=2.当t=1时,直接计算可知在G(2)中,顶点0的入度indeg(0)=2.当t=2时,在G(22)中,indeg(0)=8.下面假设t≥3.若α=a+bi∈Z2t[i],且α5=0,则显然α为零因子,即2|(a+b).故,或者2同时整除a与b,或者2⫮ab.如果2⫮ab,由于2|(a+b),令a=2d-b,d为整数,代入同余式(11)并整理得

b2(8bd-b2-4d2)≡4d3(2b-d)(mod2t-2).

由于2⫮b,故2⫮b2(8bd-b2-4d2).但2|4d3(2b-d),且t-2≥1,因此上面的同余式不成立.这就是说,当2⫮ab时,α5≠0.因此,当t≥3时,必有2同时整除a与b.

令a=2ma1,b=2μb1,其中2⫮a1b1,m与μ为正整数.又令s=min{m,μ}.显然当α=a+bi满足条件(13)时,必有α5=0.此时这样的α共有22(t-「t/5⎤)个.下面令1≤s≤「t/5⎤-1.

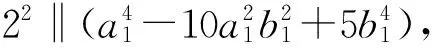
2「t/5⎤-1‖a, 2「t/5⎤-1‖b

(18)

时,α5=0.此时,这样的α共有22(t-「t/5⎤)个.

当m>μ=s时,若α5=0,则由同余式(10)得

(19)

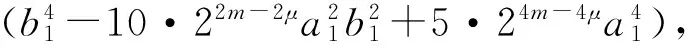
当μ>m=s时,若α5=0,则由(9)式可得

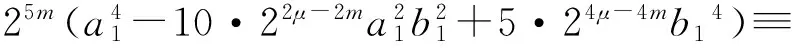
(20)

同理可证,上述同余式在μ>m时不成立.所以,此时α5≠0.

综上所述,可知当n=2t且t≡3,4,5(mod5)时,α5=0当且仅当α=a+bi满足条件(13).此时indeg(0)=22(t-「t/5⎤).当t≡1,2(mod5)时,α5=0当且仅当α=a+bi满足条件(13)或(18).此时,indeg(0)=2×22(t-「t/5⎤)=22(t-「t/5⎤)+1.定理得证.

定理9假设p是素数且p≡1(mod4).令α∈D(Zp[i])且α≠0,若α在G(p)中的入度大于0,则

证明因为p≡1(mod4),故存在正整数a与b使p=a2+b2=(a+bi)(a-bi).由文献[9]的定理2和5得,Zp[i]≅Z[i]/〈a+bi〉⊕Z[i]/〈a-bi〉≅Zp⊕Zp.显然Zp⊕Zp中非零的零因子形式为(x,0)或者(0,x),其中x∈{1,2,…,p-1}.假设元素α=(0,x)∈Zp⊕Zp,若α的入度大于0,则存在γ=(0,d)∈D(Zp⊕Zp),使得γ5=α,即

d5≡x(modp).

(21)

若p=5,易知同余方程(21)的解数为1.若p≠5,由引理1可知,同余方程(21)的解数等于gcd(5,p-1).显然,当p≡1(mod5),即p≡1(mod20)时,gcd(5,p-1)=5;当p≢1(mod5),即p≡9,13,17(mod20)时,gcd(5,p-1)=1.所以,当p≡1(mod20)时,indeg(α)=5;当p≡5,9,13,17(mod20)时,indeg(α)=1.同理,对于形如(x,0)的零因子,亦有相同的结论.定理得证.

定理10设n为非零的正整数,则:

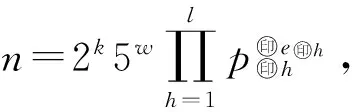
2) 0是G(n)中的孤立不动点,当且仅当n是奇数且n无平方因子.

证明由孤立不动点的定义,可知1(或0)是孤立不动点当且仅当indeg(1)=1(或indeg(0)=1).根据定理7及定理8直接计算便可证明该定理.

定理11设n为非零的正整数,则:

2) G2(n)的每一个连通分支恰好是孤立圈,当且仅当n为以下2种情形之一:

(a)n=p,其中p是素数且p≡3(mod4)或p≡5,9,13,17(mod20);

(b)n=p1p2…pm,其中m≥2,p1,p2,…,pm是互不相同的素数且ps≡3,5,7,9,13,17(mod20),s=1,2,…,m.

3) G(n)的每一个连通分支恰好是孤立圈,当且仅当n=p1p2…pm,其中m≥1,p1,p2,…,pm是互不相同的素数且ps≡3,5,7,9,13,17(mod20),s=1,2,…,m.

证明1) 由引理1知道,在映射图G1(n)中,任意顶点的入度或者等于单位元1的入度,或者等于0.从而G1(n)的每一个连通分支恰好是孤立圈当且仅当indeg(1)=1.由定理10即可证明结论成立.

2) 首先,若G2(n)的每一个连通分支恰好是孤立圈,则0必定是孤立不动点,由定理10,可知n必是若干个不同的奇素数的乘积.

反之,若n=p,p为奇素数.则当p≡3(mod4)时,由引理2,Zp[i]是域.故G2(p)仅有一个元素0,显然0所在的分支为孤立圈.当p≡1(mod4)时,由定理9知,在G2(p)中,若顶点α的入度大于0,则indeg(α)=1当且仅当p≡5,9,13,17(mod20).因此,当n=p,p为奇素数时,G2(n)的每一个连通分支恰好是孤立圈当且仅当p≡3(mod4)或p≡5,9,13,17(mod20).

另一方面,若n=p1p2,…pm,其中p1,p3,…,pm是互不相同的奇素数,m≥2,则Zn[i]≅Zp1[i]⊕…⊕Zpm[i].故G2(n)的每一个连通分支恰好是孤立圈当且仅当G(p1),…,G(pm)中每个顶点的入度均为1.下面,对p1,p2,…,pm的取值进行讨论.

当j∈{1,2,…m}且pj≡3(mod4)时,由引理2,Zpj[i]是域.因此G(pj)中每个顶点的入度均为1当且仅当在G(pj)中indeg(1)=1.由定理10(1),当pj≡3(mod4)时,在G(pj)中indeg(1)=1当且仅当pj≡3,7(mod20).

当s∈{1,2,…m}且ps≡1(mod4)时,由定理9知,在G2(ps)中,若顶点α的入度大于0,则indeg(α)=1当且仅当ps≡5,9,13,17(mod20).进一步地,可以推出,当ps≡5,9,13,17(mod20)时,G2(ps)的所有顶点入度均为1.又由定理10的1)知,当ps≡1(mod4)时,在G1(ps)中每个顶点的入度均为1当且仅当ps≡5,9,13,17(mod20).从而,当ps≡1(mod4)时,G(ps)每个顶点的入度均为1当且仅当ps≡5,9,13,17(mod20).

3) 根据定理11的1)和2)的结论即得.

定理12设n为非零的正整数,则:

1) G1(n)中不包含长度大于1的圈,当且仅当n=2,4,8或5t,t≥1;

2) G2(n)中不包含长度大于1的圈,当且仅当n是下面任一种形式:

2t,5t,qt,5t×2l,其中q是模4余3的素数,
t≥1,l∈{1,2,3}.

(22)

证明1) 首先,令n=2k.当k=1,2,3时,由引理3可知,对于α∈U(Z2k[i]),均有o(α)|4.因此,1是最小的正整数使5t≡1(modo(α)).由文献[15]的定理2.5得,G1(2k)不包含长度大于1的圈.若k>3,这时U(Z2k[i])≅Z2k-1⊕Z2k-2⊕Z4.由于k>3,故8|2k-1.从而循环群Z2k-1中必存在8阶元.由文献[15]的定理2.5,此8阶元位于G1(2k)中长为2的圈.因此,当n=2k时,G1(2k)不包含长度大于1的圈当且仅当k=1,2,3.

其次,令n=qt,t≥1,q为素数且q≡3(mod4).由引理3可知,U(Zn[i])≅Zqt-1⊕Zqt-1⊕Zq2-1.注意到8|(q2-1),因此循环群Zq2-1必存在8阶元.由文献[15]的定理2.5,此8阶元位于G1(qt)的长为2的圈上.

最后,令n=pt,t≥1,p为素数且p≡1(mod4).由引理3,当p=5时,对于α∈U(Z5t[i]),5⫮o(α)当且仅当o(α)=1,2,4.因此根据文献[15]的定理2.5得,G1(5t)不包含长度大于1的圈.当p≠5时,由引理3,循环群Zp-1是U(Zpt[i])的一个子群.如果22‖(p-1),则p-1=22m,这里2⫮m,从而m≠1,2,4,5.因此,循环群Zp-1中显然存在m阶元.从而,该m阶元位于长度大于1的圈上.如果8|(p-1),显然循环群Zp-1必存在8阶元.由文献[15]的定理2.5,此8阶元位于G1(pt)的长为2的圈上.

所以,由引理5,即得G1(n)不包含长度大于1的圈,当且仅当n=2,4,8或5t,t≥1.

2) 一方面,证明当n为(22)式中任一种形式时,G2(n)中不包含长度大于1的圈.

首先,令n=2t或qt,t≥1.由引理2,Zn[i]为局部环,因此G2(n)仅有0元素在圈上,故G2(n)不包含长度大于1的圈.

其次,假设n=5t,t≥1.由文献[9]的定理5有:Z5t[i]≅Z5t⊕Z5t.由于剩余类环Z5t是局部环,因此Z5t的非零的零因子都不在圈上.另外,剩余类环Z5t的单位群同构于Z5t-1×Z4.因此,由文献[15]的定理2.5得,Z5t的单位群中没有元素位于圈长超过1的圈上.从而,由引理5,即知G1(5t)及G2(5t)均不包含长度大于1的圈.

最后,令n=5t×2l,t≥1,l∈{1,2,3}.前面已证得G(5t)不包含长度大于1的圈,并且由本定理的结论1),当l=1,2,3时,G1(2l)不包含长度大于1的圈,又由于G2(2l)仅有0元素位于圈上,所以,由引理5,即知G2(n)不包含长度大于1的圈.

另一方面,当n不属于(22)式的任一种形式时,G2(n)中必包含长度大于1的圈.

首先,假设n=2kP1,P1是奇数,k>3.由本定理的结论1),G1(2k)中包含长度大于1的圈,因此,根据引理5,G2(n)中必包含长度大于1的圈.

其次,假设n=2kP2,P2是奇数且P2≠5,k=1,2,3.由本定理的结论1),G1(P2)中包含长度大于1的圈,因此,根据引理5,G2(n)中必包含长度大于1的圈.

最后,假设n含有至少2个不同的奇素数因子,同理可知,G2(n)中必包含长度大于1的圈.

根据定理12,G1(5t)不包含长度大于1的圈,t≥1.事实上,G1(5t)中恰好有16个元素位于长度为1的圈上,这些元素的阶分别为1,2,4.因此,G1(5t)共有16个分支.易知,当t=1时,对于G1(5)的顶点α,o(α)=2当且仅当α=4,2i,3i.而o(α)=4当且仅当α=2,3,i,4i,1+i,1+4i,2+2i,2+3i,3+2i,3+3i,4+i,4+4i.当t=2时,在G1(52)中,o(α)=2当且仅当α=24,7i,18i.而o(α)=4当且仅当α=7,18,i,24i,3+3i,3+22i,4+4i,4+21i,21+4i,21+21i,22+3i,22+22i.

从上面的例子可以看到,在G1(5)和G1(52)中,顶点x+yi在1-圈上当且仅当顶点y+xi在1-圈上.实际上,这一结论对于任意的映射图G(n)都成立.这是因为,当α=x+yi时,α5=α当且仅当同余式(1)与(2)同时成立.现在令β=y+xi,则β5=(y5-10x2y3+5x4y)+(x5-10x3y2+5xy4)i.可见,当同余式(1)与(2)均成立时,即得β5=β.因此,有以下定理.

定理13设n为正整数,在映射图G(n)中,顶点x+yi在1-圈上当且仅当顶点y+xi在1-圈上.

由引理1易知,G1(n)中每个顶点的入度或者等于顶点1的入度,或者等于0,故G1(n)总是正则图或半正则图.但对于G2(n)而言,其半正则性比较复杂.下面,讨论G2(n)的半正则性.

定理14设n=pk为素数p的方幂,k≥1,则:

1) 当n=2k时,G2(2k)是半正则的当且仅当k≤3;

2) 当n=5k时,G2(5k)是半正则的当且仅当k≤2;

3) 当n=pk且p≡11(mod20)时,G2(pk)是半正则的当且仅当k≤5;

4) 当n=pk且p≡3,7,19(mod20)时,G2(pk)是半正则的当且仅当k≤6;

5) 当n=pk且p≡9,13,17(mod20)时,G2(pk)是半正则的当且仅当k=1;

6) 当n=pk且p≡1(mod20)时,对于k≥1,G2(pk)都不是半正则的.

证明1) 设n=2k.当k=1,2时,容易验证对于Z2k[i]中的任一个零因子α,均有α5=0.故在G2(2k)中,对于非零的零因子α,都有indeg(α)=0.故G2(2)与G2(22)均是半正则的.

当k=3时,设α=a+bi∈D(Z2k[i]).如果a与b均为偶数,则同余式(9)和(10)成立,所以α5=0.如果a与b均为奇数,由于22‖a(a4-10a2b2+5b4),22‖b(b4-10a2b2+5a4),令a(a4-10a2b2+5b4)=22m,b(b4-10a2b2+5a4)=22μ,其中2⫮mμ,则23|22(m-1)且23|22(μ-1),从而a5-10a3b2+5ab4≡4(mod23),且b5-10a2b3+5a4b≡4(mod23).所以,α5=4+4i.又由于a,b∈{0,1,…,23-1},故当a与b均为奇数时,形如a+bi的元素共有16个,所以indeg(4+4i)=16.并且,由引理8有indeg(0)=16.又由引理3,|D(Z2k[i])|=32,因此当α≠0,4+4i时,indeg(α)=0.故G2(23)是半正则的.

当k≥4时,可以证明G2(2k)不是半正则图.令β=(1+i)5=-4-4i,则indeg(β)>0.假设α=a+bi∈D(Zn[i])且满足α5=β,则可以得到

a5-10a3b2+5ab4≡-4(mod2k),

(23)

b5-10a2b3+5a4b≡-4(mod2k).

(24)

由同余式(23)及(24)可以知道a,b都是奇数,且(23)×b-(24)×a得

4(a-b)[ab(a2+b2)(a+b)+1]≡
0(mod2k).

(25)

又因为a,b都是奇数,所以ab(a2+b2)(a+b)+1为奇数.由(25)式得a≡b(mod2k-2).令b=a+2k-2ν,其中ν为整数.由于k≥4,有2k-4≥k,则

b2=a2+22k-4ν2+2k-1aν≡
a2+2k-1aν(mod2k),

(26)

b4≡a4+22k-2a2ν2+2ka3ν≡
a4(mod2k).

(27)

将同余式(26)和(27)代入(23)式得:a5≡1(mod2k-2),此方程的解数等于1,即a≡1(mod2k-2).由于a∈{0,1,…,2k-1},所以在此集合中,满足a5≡1(mod2k-2)的元素个数为22.同理,也可得到b5≡1(mod2k-2),故在集合{0,1,…,2k-1}中,满足b5≡1(mod2k-2)的元素个数为22.所以,由(23)和(24)式构成的方程组的解数为24.所以indeg(-4-4i)=24.又由定理8知,k≥4时,indeg(0)≠24.因此当k≥4时,G2(2k)不是半正则的.

2) 设n=5k.当k=1时,由定理6,G(5)的不动点个数为52.又显然Z5[i]的元素个数为52.因此在G(5)中,每个顶点都在1-圈上,从而G2(5)是正则的,也是半正则的.

当k=2时,由定理12的2)得,G2(52)中不含长度大于1的圈.且由定理6的3)的证明过程可知,Z52[i]中恰有9个零因子为不动点.直接验证可知,以下9个零因子均为不动点:

0,9+12i,9+13i,12+9i,12+16i,13+9i,
13+16i,16+12i,16+13i.

并且,上述零因子的入度均为25.由于Z52[i]共有25×9个零因子,因此,除了上述零因子之外,其他零因子的入度均为0.故G2(52)是半正则的.

现在令k≥3.由定理6的3)证明过程可知,Z5k[i]中恰有9个零因子为不动点,这9个不动点的入度均大于0.并且,由该证明过程还可得,如果α=x+yi为G2(5k)中的不动点,则(2x)4≡1(mod5k).令β=(2+i)5=-38+41i∈Z5k[i].显然β是Z5k[i]的零因子,且indeg(β)>0.但是,由于(2×(-38))4≢1(mod53),所以,对于k≥3均有(2×(-38))4≢1(mod5k).因此,当k≥3时,β不是G2(5k)的不动点.所以,G2(5k)至少有10个零因子的入度大于0.若G2(5k)是半正则的,则由定理8知,这10个零因子的入度均等于indeg(0)=52(k-「k/5⎤).从而,|D(Z5k[i])|≥52(k-「k/5⎤)×10.然而,由引理3得|D(Z5k[i])|=52k-2×9.显然,当k≥3时,必有52(k-「k/5⎤)×10>52k-2×9=|D(Z5k[i])|,矛盾.因此,当k≥3时G2(5k)不是半正则的.

3) 设n=pk.当p≡11(mod20)时,由引理3及定理8知,对于k≤5,有|D(Zpk[i])|=indeg(0).因此对于Zpk[i]的任一个零因子α,均有α5=0.从而G2(pk)是半正则的.

假设k≥6.令β=p5,显然indeg(β)>0.假设α=a+bi∈D(Zpk[i])且满足α5=β.则有以下同余式成立:

a5-10a3b2+5ab4≡p5(modpk),

(28)

b5-10a2b3+5a4b≡0(modpk).

(29)

显然,必有p|a且p|b.令a=psa1,b=phb1,s与h均为正整数,p⫮a1b1.由(28)式得

(30)

若s>1,同余式(30)的左边显然是p的倍数,故此同余式不成立.因此,有s=1.另外 ,如果h=s=1,则由(p(a1+b1i))5=p5∈D(Zpk[i])得a1+b1i是Zpk-5[i]的5阶元.但由引理3可知Zpk-5[i]的5阶元只有5个,即为剩余类环Zpk-5中的5阶元.因此,当p⫮a1b1时,a1+b1i不可能是Zpk-5[i]的5阶元.故必有h>1.所以由(29)式得

(31)

由于h>1,因此h+4<3h+2<5h.故由(31)式得h+4≥k,即h≥k-4.所以pk-4|b.又由同余式(30)式得

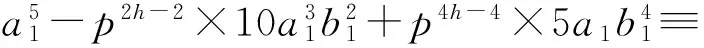
(32)

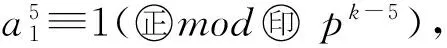
4) 设n=pk,p≡3,7,19(mod20).当k≥7时,由于方程a15≡1(modpk-5)的解数为gcd(5,p-1)=1,所以与本定理情形3)类似可证得,满足α5=p5的元素α共有p4×p4=p8个.因此indeg(p5)=p8.但是,由定理8知,k≥7时,indeg(0)>p8.所以当k≥7时,G2(pk)不是半正则的.

当k=6时,由定理8知indeg(0)=p8.令

B={p5(x+yi)5∈D(Zp6[i]):x,y=0,1,…,p-1}.

显然,对于β∈B,indeg(β)>0.与本定理情形3)的讨论类似,可得indeg(β)=indeg(p5)=p8=indeg(0).又因为|B|=p2,且|D(Zp6[i])|=p10=p2×p8=|B|×indeg(β),所以对于α∈D(Zp6[i])且α∉B,都有indeg(α)=0.所以当k=6时,G2(p6)是半正则的.

当k≤5时,与本定理情形3)的证明相同,可知G2(pk)是半正则的.

5) 设n=pk,p≡9,13,17(mod20).当k=1时,由定理8,indeg(0)=1.又由定理11,G2(p)的每一个顶点的入度均为1,所以G2(p)是半正则的.

当k≥2时,由于p≡1(mod4),所以存在正整数x和y,使得p=x2+y2.令

C={d5(x+yi)5∈D(Zpk[i]):d=0或d∈U(Zpk)}.

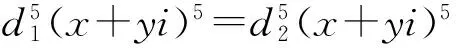
6) 设n=pk,p≡1(mod20).当k=1时,由定理9,对于α∈D(Zp[i]),且α≠0,如果indeg(α)>0,则indeg(α)=5.然而由定理8,indeg(0)=1,所以G2(p)不是半正则的.

当k>1时,方程d5≡1(modpk)的解数为gcd(5,p-1)=5.故|C|=φ(pk)/5+1=(p-1)pk-1/5+1.与本定理情形5)的讨论过程相似,可知在k>1时,G2(pk)不是半正则的.

2 结束语

对于高斯整数环商环的5次幂映射图结构的研究结果及方法,为研究这一商环的任意k次幂的映射图提供了一个方案,因为随着次数k的增大,(a+bi)k的展开式会变得比较复杂,从而对映射图结构的研究难度会加大.

[1] 廖欢,廖群英. 关于有限域上特殊本原元的存在性[J]. 四川师范大学学报(自然科学版),2015,38(6):797-801.

[2] 韦扬江,唐高华. The square mapping graphs of the ringZn[i][J]. 数学杂志,2016,36(4):676-682.

[3] MEEMARK Y, MAINGAM N. The digraph of the square mapping on quotient rings over the Gaussian integers[J]. Inter J Number Theory,2011,7(3):835-852.

[4] 韦扬江,梁艺耀,唐高华,等. 模n高斯整数环的商环的立方映射图[J]. 广西师范大学学报(自然科学版),2016,34(3):53-61.

[5] WEI Y J, NAN J Z. The cubic mapping graphs for the ring of Gaussian integers modulon[J]. Czech Mat J,2011,136:1023-1036.

[6] WEI Y J, NAN J Z, TANG G H. Structure of cubic mapping graph for the ring of Gaussian integers modulon[J]. Czech Math J,2012,137:527-539.

[7] 唐高华,苏华东,赵寿祥.Zn[i]的零因子图的性质[J]. 广西师范大学学报(自然科学版),2007,25(4):32-35.

[8] 苏华东,唐高华.Zn[i]的素谱和零因子[J]. 广西师范学院学报(自然科学版),2006,23(4):1-4.

[9] DRESDEN G, DYMEK W M. Finding factors of factor ring over the Gaussian Integers[J]. Am Math Month,2005,112:602-611.

[10] 唐高华,苏华东,易忠.Zn[i]的单位群结构[J]. 广西师范大学学报(自然科学版),2010,28(2):38-41.

[11] CROSS J T. The Eulerφ-function in the Guassian integers[J]. Am Math Month,1983,90:518-528.

[12] FREUDENBERGER J, GHABOUSSI F, SHAVGULIDZE S. New coding techniques for codes over Gaussian integers[J]. IEEE Tran Commun,2013,61(8):3114-3124.

[13] DENG G X. Cycles of linear dynamical systems over finite local rings[J]. J Alge,2015,433:243-261.

[14] 潘承洞,潘承彪. 初等数论[M]. 北京:北京大学出版社,1992.

[15] WEI Y J, TANG G H. The iteration digraphs of finite commutative rings[J]. Turk J Math,2015,39:872-883.

[16] WEI Y J, TANG G H, SU H D. The commuting graphs of some subsets in quaternion algebras over the ring of integers modulon[J]. Indian J Pure Appl Math,2011,42(5):387-402.