丢番图方程x3－1=1 477y2的整数解

党 荣

(渭南师范学院东盟博仁财经学院，陕西渭南714099)

0 引言

丢番图方程，又名不定方程，是指变量个数大于方程个数且解为整数值的方程(或方程组)。它与组合数学、代数几何和代数编码等学科有着密切的联系。近年来，许多中外学者在代数数论、组合数论和群论等数学分支中都提出了一些丢番图方程问题，它的研究成果不仅对数学的各个分支起着推动作用，而且对非数学学科，例如计算机科学、电子学、信号数字处理等有着重大的实际意义。

求解丢番图方程的方法有很多种，初等方法和非初等方法都可以予以证明，长期以来一直受到数论研究者的关注，特别是对Pell方程x3－Dy2=±1的研究已取得了许多成果，Pell方程理论对于求解其他丢番图方程的整数解问题有着很大的帮助。

方程x3±1=Dy2(D＞0)是一类重要的丢番图方程，其整数解已经有不少人研究过。柯召、孙琦［1－2］证明了x3－Dy2=±1当D＞2，D无平方因子且不含6k+1型的素因子时，方程x3－Dy2=±1无平凡整数解。但当D含6k+1型的素因子时，该方程的非平凡整数解的求解较为困难。李双志、罗明［3］给出了方程x3+1=201y2的所有整数解。韩云娜［4］给出了方程x3－1=38y2的所有整数解。曹珍富等人［5－6］给出了丢番图方程更一般的求解理论。段辉明［7］讨论了方程x3+1=57y2的整数解问题。陈斌［8－9］讨论了与其相关的一类不定方程的整数解问题。然而关于x3－1=1 477y2这类方程的整数解的问题至今无人研究和讨论。本文利用初等方法讨论和研究得出了该丢番图方程x3－1=1 477y2的整数解。

1 引理

由一类丢番图方程x3±1=Dy2(D＞0)的研究结果可知，想要求解丢番图方程x3－1=1 477y2的整数解，首先需要引入以下几个引理。

引理1［5］方程4x4－3y2=1仅有整数解(x，y)=(±1，±1)。

引理2［5］设p是一个素数，则方程x4－py2=1(p＞0)当p≠5和p≠29时无平凡解。

引理3［6］方程x2－3y4=1有整数解 (x，y)=(±2，±1)，(±7，±2)，(±1，±0) 。

2 定理及其证明

定理1 丢番图方程

仅有平凡整数解 (x，y)=(1，0)和非平凡整数解 (x，y)=(212 688，2 552 256)。

证明 根据引理可知，要证明丢番图方程x3－1=1 477y2有无整数解，需考虑形如

的丢番图方程的整数解问题，进而考虑方程

因为gcd(x－1，x2+x+1)=1或3，所以可以给出方程x3－1=1 477y2以下8种有可能的组合形式:

(A)x－1=1 477u2，x2+x+1=v2，y=uv，gcd(u，v)=1;

(B)x－1=u2，x2+x+1=1 477v2，y=uv，gcd(u，v)=1;

(C)x－1=7u2，x2+x+1=211v2，y=uv，gcd(u，v)=1;

(D)x－1=211u2，x2+x+1=7v2，y=uv，gcd(u，v)=1;

(E)x－1=4 431u2，x2+x+1=3v2，y=3uv，gcd(u，v)=1;

(F)x－1=3u2，x2+x+1=4 431v2，y=3uv，gcd(u，v)=1;

(G)x－1=21u2，x2+x+1=633v2，y=3uv，gcd(u，v)=1;

(H)x－1=633u2，x2+x+1=21v2，y=3uv，gcd(u，v)=1。

可以根据方程分解的以上8种形式进而给出方程(1)的整数解。

根据第一种情况(A)解出第二式，得到x=0和－1，都不能满足第一个式子所给出的条件，所以在这种情形下方程(1)无整数解。因为，利用同余理论的基本性质可以得出(C)(F)(H)也不成立。

根据第二种情况(B)把第一个式子代入第二式得到

则有(2u2+3)2+3≡0(mod211)，即u2≡46，72(mod211)。

但是模211的勒让德符号为

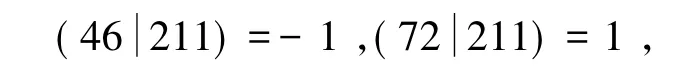
所以在这种情形下方程(1)无整数解。

根据情形(D)，由第一个式子得到

将情形(D)代入第二个式子中得到

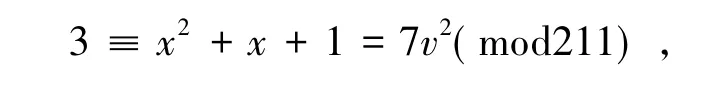
从而计算出模211的勒让德符号值为

所以这种情形下方程(1)无整数解。

根据情形(G)，由第一个式子得到

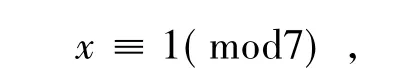
代入到第二个式子中得

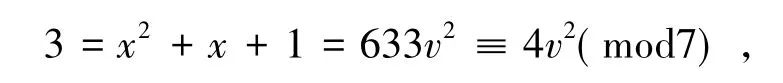
从而得到模7的勒让德符号为

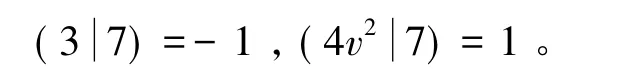
所以这种情况下方程(1)无整数解。

根据情形(E)，将第一个式子带入第二个式子中得到

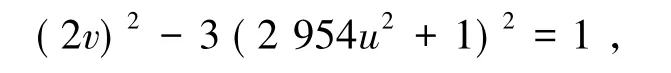
因而得到该情形下

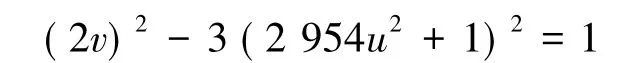
的全部整数解可表示为

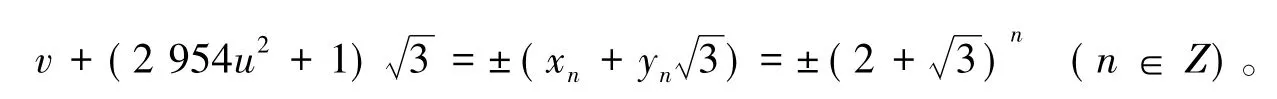
其中:(2，1)是 Pell方程

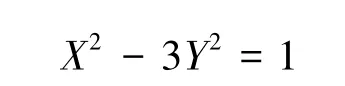
的基本解，所以有

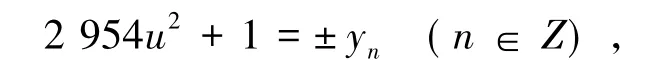
即

又因为

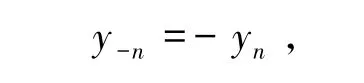
所以只需要考虑

由式(3)可以得到

则有

容易验证下列两式成立:

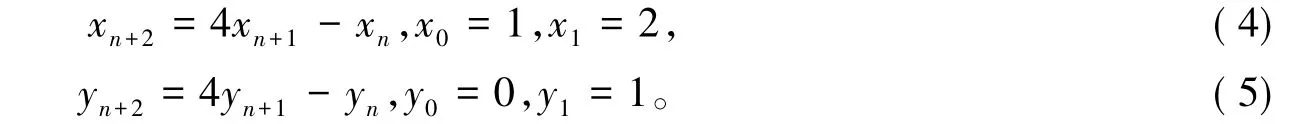
因而需要对递归序列式(5)取模1 477，得到周期为40的剩余类序列。

当且仅当n≡0(mod20)时，有

仅当n≡1，9(mod40)时，得出

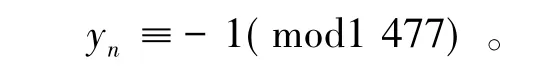
所以只有当n≡1，9(mod40)时式(3)才成立。

而当n≡1(mod40)时，设n=40m+1(m∈Z)，则有

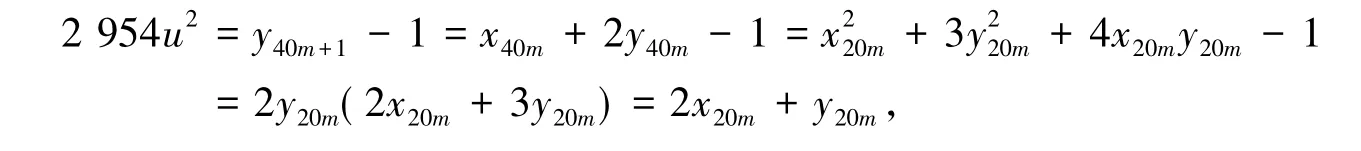
即得到了

又因为

而

所以式(6)可分解为下列式:

由引理1知y20m+1=±1，则m=0，此时n=1。由式(3)得

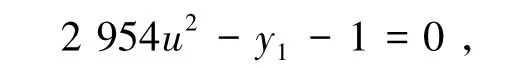
则有u=0，从而计算出方程(1)的平凡整数解为(x，y)=(1，0)。

当n≡9(mod40)时，设n=40m+9(m∈Z)，则

即

同理，又对递归序列(4)取模211，得周期为20的剩余类序列。当且仅当n≡±5(mod20)时，有

故

又gcd(x20m+5，y20m+4)=2，所以式(8)可以分解为下面两种情况:

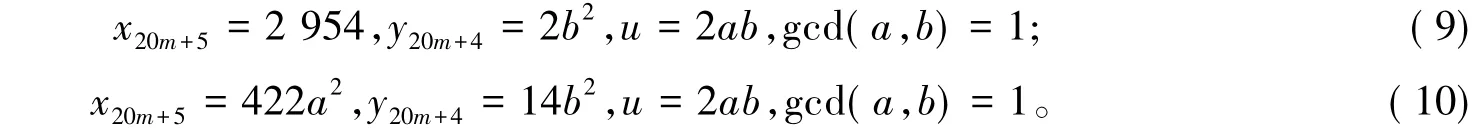
由式(9)的第二式得到

即

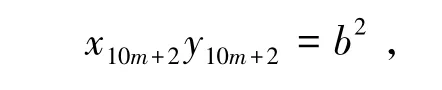
又因为gcd(x10m+2，y10m+2)=1，则可以分解为以下形式

由引理(2)可知，d=0。

所以y10m+2=0，显然没有整数解。所以这种情形下方程(1)无整数解。

由式(10)的第二式得

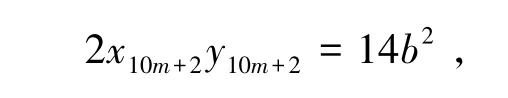
即

又gcd(x10m+2，y10m+2)=1，则可以分解为以下两种形式:

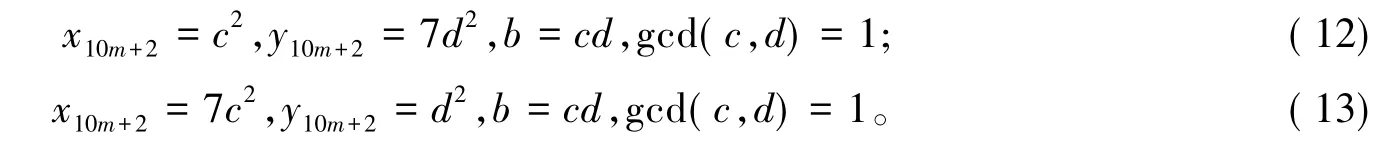
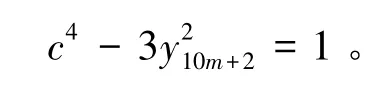
由引理2可知y10m+2=0，显然没有整数解。

所以这种情形下方程(1)无整数解。

由引理3可知，d=±2，则m=0，此时n=9，由式(3)得

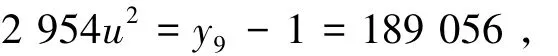
则有u=±4，从而计算出方程(1)的整数解(x，y)=(212 688，2 552 256)。

综上所述可知，丢番图方程(1)有整数解 (x，y)=(1，0)，(212 688，2 552 256) 。

3 程序算法分析验证

对于丢番图方程x3－1=1 477y2，运用Maple小程序，可以设计得出其算法流程如下:

图1 Maple程序运行结果分析图

参考文献:

［1］柯召，孙琦．关于丢番图方程x3±1=Dy2［J］．中国科学，1981，24(12):1453－1457．

［2］柯召，孙琦．关于丢番图方程x3±1=3Dy2［J］．四川大学学报(自然科学版)，1981，18(2):1－5．

［3］李双志，罗明．关于不定方程x3+1=201y2［J］．西南师范大学学报(自然科学版)，2010，35(1):11－14．

［4］韩云娜．关于 Diophantine方程x3－1=201y2［J］．科学与技术工程，2010(10):169－171．

［5］曹珍富．关于丢番图方程引论［M］．哈尔滨:哈尔滨工业大学出版社，2012:180－187．

［6］杜先存，万飞，杨惠章．关于丢番图方程x3±1=1267y2［J］．数学的实践与认识，2013，43(15):288－292．［7］段辉明．关于丢番图方程x3+1=57y2［J］．重庆师范大学学报(自然科学版)，2010，27(3):41－43．

［8］陈斌．特殊函数理论及其应用研究［M］．西安:陕西科学技术出版社，2015．

［9］陈斌．关于不定方程x3+1=3y2的解［J］．渭南师范学院学报，2010，25(2):15－17．