基于莫尔条纹的波干涉演示仪的设计与制作
韩修林,唐义甲,丁智勇
(阜阳师范学院物理与电子工程学院,安徽阜阳236037)
频率相同、波动方向一致且位相差恒定的同种性质两列波在波动空间相遇叠加,使某些区域的波动始终加强,某些区域的波动始终减弱,而且振动加强的区域和振动减弱的区域相互隔开的现象称为波的干涉。干涉现象是波动形式所独具的重要特征之一,是波动光学、声学、量子力学等的理论基础,对近代物理学的发展也有重大作用[1],因而波的干涉一直是大学物理教学的重点。由于其理论较为抽象,也一直是大学物理教学的难点。
为了加深对波的干涉这一物理概念、物理规律的理解,强化记忆,培养学生观察能力和分析问题、解决问题的能力,大多采用演示实验来辅助课堂教学。通常演示波的干涉实验时采用投影器——发波水槽或采用课件。然而,这两种方法都存在一定的不足:采用传统的投影器——发波水槽,仪器笨重,搬动不便,且演示效果易受到外部环境干扰而不明显;采用多媒体课件教学,教师操作较方便,但干涉这一物理现象学生难以真切地体会和感受,只能从虚拟的图像中感知这一物理概念和规律。为此,笔者基于光栅莫尔效应形成机理设计制作了一个较为理想的演示装置,该装置克服了以上传统演示仪存在的缺点,能较好地演示波的干涉现象及其规律。
1 设计原理
莫尔光栅分粗光栅和细光栅。栅距远大于波长的光栅叫粗光栅,栅距接近于波长的光栅叫细光栅,本文所涉及的莫尔光栅皆为粗光栅。两块光栅相向叠合时,在相干或非相干光的照明下,在叠合面上将出现明暗相间的条纹,称为光栅莫尔条纹。粗光栅因栅节距远远大于光波波长,所以对照射光的衍射不明显,其莫尔条纹形成的机理只能用遮光阴影原理来阐释。[2]
1.1 线性光栅莫尔条纹形成机理
线性光栅是由一族排列紧密、均匀、等宽等间距的平行直线所组成,如图1所示,a为光栅线(不透光)宽度,b为相邻光栅线之间(透光部分)间距,d=a+b称为光栅栅距常数,也称为栅节距。两块栅距常数相同的线性光栅,其栅面相向叠合并且使两者栅线有很小的交角θ,则由于遮光效应,在光栅线交叉点近旁的小区域内由于不透光的暗纹重叠,因而遮光面积最小,挡光效应最弱,光的累积作用使得这个区域出现亮条纹。相反,距光栅线交叉点较远的区域,因两光栅不透光的栅线的重叠部分变得越来越少,不透明区域面积逐渐变大,即遮光面积逐渐变大,使得挡光效应变强,只有较少的光线能通过这个区域透过光栅,使这个区域出现暗条纹,如图2所示,这些相间出现的亮、暗条纹就是莫尔条纹[3]。

图1 线性光栅图
若称重叠的两光栅底下光栅为主光栅,上面光栅为副光栅,并对主光栅线进行编序,序数m为(…,-2,-1,0,+1,+2,…),对副光栅线编序,序数n为(…,-2,-1,0,+1,+2,…)。从图 1 还可以看到,相间出现的亮、暗带可由主副栅线序数(m,n)确定,若令k=m-n,每一个k值都对应着一条亮带。例如,k=0的亮带由(-3,-3),(-2,-2),(-1,-1),(0,0)(1,1),(2,2),(3,3)等交点簇形成,k= -1 的亮带由(-2,-1),(-1,0),(0,1)(1,2),(2,3),(3,4)等交点簇形成,而k=1 的亮带是由(-2,-3),(-1,-2),(0,-1)(1,0),(2,1),(3,2)等交点簇形成。相邻亮带中间有条暗带,它们相互平行,间距相等。[4-5]

图2 线性光栅莫尔条纹图样
1.2 线性光栅莫尔条纹与平面波干涉图样间的联系
若把线性光栅的0号光栅线看成平面波的源波阵面,其他光栅线看成向外辐射波阵面,若相邻二波阵面之间的相位差是2π,则栅节距为平面波波长λ。不透光的光栅线纹看成平面谐波负半周期,线纹中心表示波谷,透光部分看成平面谐波正半周期,其中心表示波峰[5],那么就可以用线性光栅莫尔条纹表示平面波的干涉图样了,显然莫尔条纹亮带是相干波的同相位重叠区,为干涉加强区,暗纹则为相干波的反相位重叠区,是干涉减弱区。[4]k值则为干涉级数,k级干涉加强区波程差为kλ,k级干涉减弱区波程差为(k+1/2)λ,这些与平面波干涉理论完全吻合。
1.3 圆环光栅莫尔条纹形成机理
圆环光栅是由一族排列紧密、均匀、等宽等间距的同心圆环线所组成,如图3所示,a为光栅线(不透明)宽度,b为相邻光栅线之间间距,d=a+b称为光栅栅距常数。两块栅距常数相同的圆环光栅,其栅面相向叠合并且使两者圆心拉开很小的距离,由于遮光效应,同样在光栅线交叉点近旁的小区域内由于不透光的黑色线纹重叠,因而遮光面积最小,挡光效应最弱,光的累积作用使得这个区域出现亮带。相反,距光栅线交叉点较远的区域,因两光栅不透光的黑色线纹的重叠部分变得越来越少,不透明区域面积逐渐变大,即遮光面积逐渐变大,使得挡光效应变强,只有较少的光线能通过这个区域透过光栅,使这个区域出现暗带。如图3所示,两光栅重叠区形成明暗相间的双曲线簇条纹。[2-5]

图3 同心圆环光栅莫尔条纹图样
同样,我们称相互重叠两光栅下面光栅为主光栅,上面光栅为副光栅,并规定从环心向外光栅线序数依次为0,1,2,3,…则从图3中我们还可以看到,两圆环光栅形成双曲线簇莫尔条纹可由主副光栅线序数(m,n)确定,其中m-n是任意整数,若以两圆环光栅环心连线为x轴,两圆环光栅环心直线中垂线为y轴建立直角坐标系,为了便于说明问题,不妨令两圆环光栅环心之距为2c,则明纹上任一点P(x,y)到主光栅环心(-c,0)的距离为:

到副光栅环心(c,0)的距离为:

式(1)减去式(2)得:
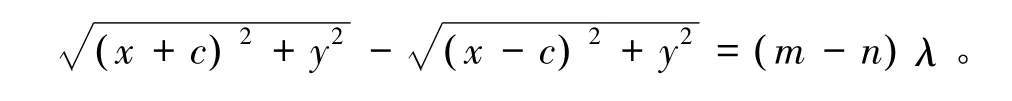
令k=m-n,即

显然,式(3)为一簇双曲标准方程,每一个k值都对应着一支双曲明纹,正值k对应左支双曲线簇,负值k对应右支双曲线簇。[6]
1.4 同心圆环光栅莫尔条纹与球面波干涉图样间的联系
若把圆环光栅的环心看成球面谐波的波源,其他环形光栅线看成向外辐射波阵面,相邻波阵面间相位差为2π,栅节距为球面波波长λ,光栅不透光部分黑色线纹看成球面谐波负半周期,线纹中心表示波谷,光栅透光部分白色线纹看成球面谐波正半周期,中心表示波峰,那么为相干波源到相干点P(x,y)的波程差,故可以用同心圆环光栅莫尔条纹表示球面波的干涉花样了[4]。显然莫尔条纹明纹是相干波的同相位重叠区,为干涉加强区,暗纹则为相干波的反相位重叠区,是干涉减弱区。k值则为干涉级数,k级干涉加强区波程差为kλ,k级干涉减弱区波程差为(k+1/2)λ,这些与球面波干涉理论吻合得也相当好。
2 制作方法
如图4所示,演示仪的框架用轻质铝合金制成,在透明的亚克力板上刻上光栅线制成演示光栅,一块演示光栅板由框架上插槽口插入固定,不妨称为主光栅;另一块演示光栅由框架侧边插槽口插入,且能相对主光栅沿水平方向自由移动,不妨称为副光栅。

图4 莫尔效应和机械波干涉综合演示仪
3 实验方法和演示效果
在进行演示实验时,将主光栅从框架上插槽口插入固定,副光栅从侧边插槽插入,若主、副光栅相同且栅节距相等,副光栅相对主光栅静止不动,在它们重叠区出现莫尔条纹就可以用于波的干涉演示。如图4所示,(a)用于平面波干涉演示,(b)用于球面波干涉演示。栅节距表示波长λ,由v=λf(v是波速,f是频率)知两波频率相等;两栅相对静止不动表示两波相位差恒定;用线栅0号光栅线表示平面波的波源,环形光栅的环心表示相干球面波的波源,明纹区域的中心点到波源的距离kλ(k为莫尔条纹序号),暗纹区域的中心点到波源的距离(k+1/2)λ,表明波长差为kλ区域为干涉加强区,波长差为(k+1/2)λ区域为干涉减弱区。副栅相对主栅移动,表示两相干波相位差发生改变,莫尔条纹随之发生移动,表示干涉区域随之改变,说明相位差恒定才能形成稳定干涉。插入框架两栅相同但栅节距不同或不相同的两栅形成莫尔条纹凌乱不规整,说明只有性质相同、频率相同的两列波发生叠加才能形成干涉。
该演示仪通过课堂教学检验,不仅操作简便,而且演示也灵活多变,演示效果非常明显,丰富了课堂教学内容,极大地调动学生学习兴趣。
4 结语
本演示实验仪在研究波的干涉形成规律及形成干涉所需条件等干涉理论的教学辅助上,既可以用于大学课堂,也可以用于中学课堂。能形象地演示波的干涉现象,模拟的干涉条纹比较清晰。同时,它还能进一步演示出非相干波的叠加为何不能形成干涉花样。本演示实验仪的装置非常简单,便于在课堂上采用,以帮助学生全面、深入地理解波的干涉现象。
除此之外,只要对演示光栅稍加改造,还可用来模拟叠加静电场的等势线分布的演示[7],这拟另文加以讨论。通过对演示光栅改造,该演示仪还可以对莫尔光栅测距、测角传感及丰富多彩的莫尔动画进行演示[8],该演示仪不愧为一台多功能综合教学演示仪。
遗憾的是该演示仪现在还不能演示波的衍射现象及多普勒效应现象,如何用该演示仪来演示波的衍射现象及多普勒效应现象,仍在继续研究探索之中。
参考文献:
[1]程守洙,江之永.普通物理学[M].北京:高等教育出版社,2014:87-90.
[2]武克南,史国川.光栅读数系统设计[J].电脑知识与技术,2007(9):772-773.
[3]高葳,高英.论莫尔效应的发展[J].科技资讯,2013(12):78-80.
[4]朱益清,朱拓.用莫尔条纹演示波的干涉原理[J].工科物理,1998(3):5-7.
[5]喻洪麟.理想环形莫尔条纹的获取[J].计量技术,1996(12):2-3.
[6]同济大学数学系.高等数学[M].北京:高等教育出版社,2009:32-38.
[7]李治林,刘建科.利用莫尔条纹模拟叠加静电场的等势线[J].大学物理,2011,30(6):47-51.
[8]孙丽丽,房鑫盛,张家祯,等.莫尔条纹测杨氏模量实验研究[J].实验技术与管理,2016,33(10):68-70.
[9]何春娟,刘绒霞,曹磊.莫尔条纹技术在微小位移测量中的应用[J].西安工业学院学报,2005,25(6):565-567.

