OPTIMAL CONTROL OF A POPULATION DYNAMICS MODEL WITH HYSTERESIS*

Bin CHEN (陈斌)

Fujian Province University Key Laboratory of Computational Science，School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China E-mail:chenbinmath@163.com

Sergey A.TIMOSHIN†

Fujian Province University Key Laboratory of Computational Science，School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China

Matrosov Institute for System Dynamics and Control Theory，Russian Academy of Sciences，Lermontov str.134，664033 Irkutsk，Russia E-mail:sergey.timoshin@gmail.com

Abstract This paper addresses a nonlinear partial differential control system arising in population dynamics.The system consist of three diffusion equations describing the evolutions of three biological species:prey，predator，and food for the prey or vegetation.The equation for the food density incorporates a hysteresis operator of generalized stop type accounting for underlying hysteresis effects occurring in the dynamical process.We study the problem of minimization of a given integral cost functional over solutions of the above system.The set-valued mapping de fining the control constraint is state-dependent and its values are nonconvex as is the cost integrand as a function of the control variable.Some relaxationtype results for the minimization problem are obtained and the existence of a nearly optimal solution is established.

Key words optimal control problem;hysteresis;biological diffusion models;nonconvex integrands;nonconvex control constraints

1 Introduction

Given a final time T＞0 and a bounded domain Ω⊂RN，N≤3，with smooth boundary∂Ω，the primary concern of this paper is to consider the following optimal control problem:

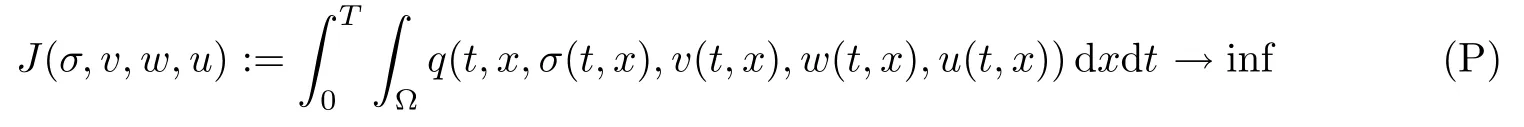
over the solution set of the dynamical control system:

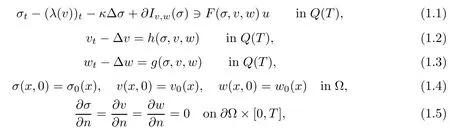
subject to the state-dependent control constraint:

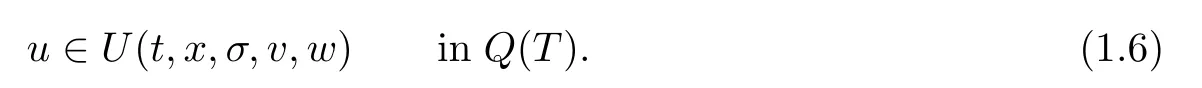
Here，Q (T):=[0，T]×Ω，κ is a given constant，σ0，v0，w0are given initial conditions，∂/∂n is the outward normal derivative on∂Ω.The operator∂Iv，w(·) is the subdifferential，in the sense of convex analysis，of the indicator function Iv，w(·) of the interval[f*(v，w)，f*(v，w)]，f*，f*:R2→R，q:Q (T)×R4→R，F，h，g:R3→R，λ:R→R are prescribed functions，U:Q (T)×R3→R is a multivalued mapping with compact，but not necessarily convex values.

We note that when w is fixed and F≡0，λ(v)=v in (1.1)，inclusion (1.1) yields the differential representation of hysteresis operator of the generalized stop type (cf.[1]).During the last three decades，hysteresis operators have been extensively applied in modeling，analysis，and control of a variety of irreversible nonlinear phenomena in applied sciences including phase transitions[2-7]，porous media flow [8-12]，thermostat models[13-17]，concrete carbonation[18-22]and many others.In the same vein，system (1.1)-(1.5)(without the control u) was introduced in[23](see also[24，25]) to model the evolution of populations in the vegetationprey-predator framework when diffusive effects in the dynamics of three species are taken into account and the food density for the prey exhibits hysteretic character.This latter means that the growth rate of the food for the prey depends not only on the current state of prey and predator populations，but it also depends on their immediately preceding density history.In[26]，with the aim to achieve a possible optimization of the population dynamics process by way of controlling the food supply for the prey this uncontrolled system was subjected to a control action and the existence of solutions for the corresponding control system (1.1)-(1.6) was established.

In our model，the unknown variables σ，v，and w represent the densities of vegetation，prey and predator，respectively，with eqs.(1.1)，(1.2)，and (1.3) characterizing the evolutions of the corresponding species.In this respect，the nonconvexity of values of U in the control constraint (1.6) is a biologically relevant assumption.

Our aim in this paper is to consider along with (P) the following alternative problem:

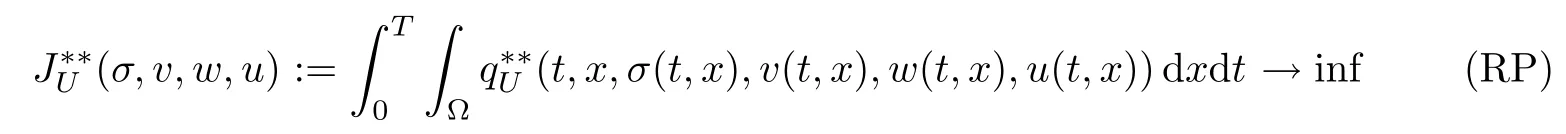
over solutions of (1.1)-(1.5) supplemented with the following alternative control constraint:

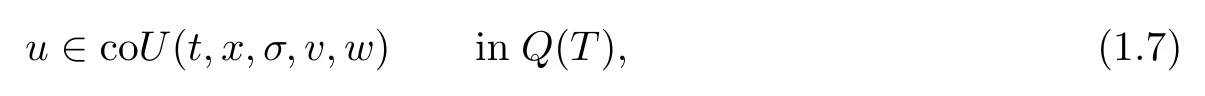
and explore some properties and relationships between problems (P) and (RP).Here，(RP) stands for the relaxed problem，coU denotes the convex hull of the set U，which is the intersection of all convex sets containing U，and for the extended real-valued function qU:Q (T)×R3×R→R∪{+∞}:

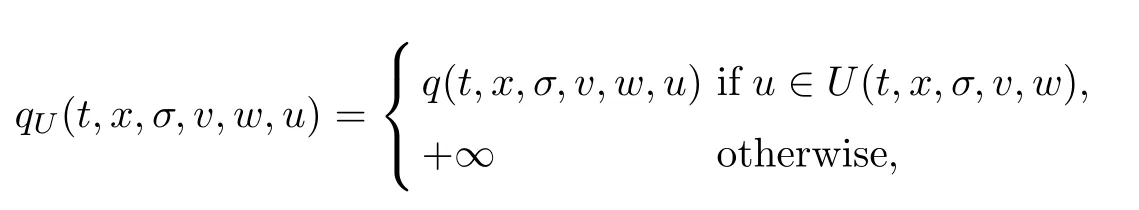
We remark that while our model has not been inspired by any particular applied problem，the results we obtain might find potential applications in analysis and control of real-world ecosystems such as spruce budworm population dynamics models.The latter describe interactions in the budworm-forest framework and include three species:boreal forest trees such as balsam fir，insect pests such as spruce budworm which feed on the foliage of trees and avian predators feeding in turn on the insects.These ecosystems are typical to Northern parts of Canada and Russia，including the lake Baikal region，where the defoliation of larches by insects and the subsequent dieback of the trees is a major problem in forest ecology.Available control actions towards preservation of forest reserve include spraying insecticides，removal of infected trees and other and affect the rate of change in the insects population.This prompted us to include the control function u into the first equation of our evolution system.On the other hand，the natural concern to avoid the total perishing of birds population caused by insufficient food supply should be reflected in optimization strategy towards minimization of forest loss.

The outline of the paper is as follows.After introducing in the next section the notation and hypotheses on the data describing problem (P)，in Section 3 we derive several continuity properties of the control-to-state solution operator associated with our control systems.These properties are instrumental in proving our main results in the last Section 4.The latter consist in establishing the existence of an optimal solution for problem (RP)，the density，in an appropriate topology，of solutions of the original control system (1.1)-(1.6) among solutions of the convexi fied control system (1.1)-(1.5)，(1.7)，and the existence of a nearly optimal，in a suitable sense，solution for problem (P).

At the end of Introduction，we mention that the existing literature on optimal control of systems exhibiting hysteretic character is sparse.It is worthwhile however to mention a seminal contribution of Brokate to this area (see[27，28]).Moreover，to the best of the authors’knowledge，there have been no contributions so far addressing optimal control problems for biological models with hysteresis.

2 Preliminary Notions，Hypotheses on the Data，and Statement of the Main Results

In this section，we fix the notation which we use throughout the paper，prove an auxiliary lemma，specify hypotheses which we posit on the data describing problem (P)，give a precise meaning in which solutions to our control systems are understood and the corresponding minimization problems are treated，and state our main results.

Let X be a Hilbert space with the inner product (·，·)X.A function φ:X→R∪{+∞}is called proper if its effective domain domφ:={x∈X;φ(x)＜+∞}is nonempty.By definition，the subdifferential∂φ(x)，x∈X，of a proper，convex，lower semicontinuous function φ is the set

∂φ(x)={h∈X;(h，y-x)X≤φ(y)-φ(x)，∀y∈X}，

and its domain is the set dom∂φ:={x∈X;∂φ(x)Ø}.It is known[29]that dom∂φ⊂domφ.

We say that a sequence of proper，convex，lower semicontinuous functions φn:X→R，n≥1，Mosco-converges[30]to a proper，convex，lower semicontinuous function φ:X→R，denoted，if:

1) for any x∈X and any sequence xn∈X，n≥1，weakly converging to x we have

2) for any x∈X there exists a sequence xn→x such that φn(xn)→φ(x).

Denote by dX(x，A) the distance from a point x∈X to a set A⊂X.Then，the Hausdorffmetric on the space of closed bounded subsets of X，denoted cb (X)，is the function:

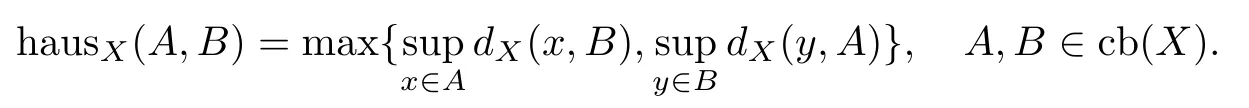
If (E，A) is a measurable space，then a multivalued mapping F:E→cb (X) is called measurable if{τ∈E;F (τ)∩CØ}∈A for any closed subset C of X.A set F of measurable functions from E to X is called decomposable if for any f1，f2∈F and any E∈A we have that f1·χE+f2·χEE∈F，where χEstands for the characteristic function of the set E.

Let Y，Z be two Banach spaces.A multivalued mapping F:Y→Z is called lower semicontinuous if for any y∈Y，z∈F (y) and any sequence yk→y，k≥1，there exists a sequence zk∈F (yk)，k≥1，which converges to z.

Given two functions f*，f*:R2→R，recall that the indicator function Iv，w(·) of the set K (v，w):=[f*(v，w)，f*(v，w)]is defined as follows

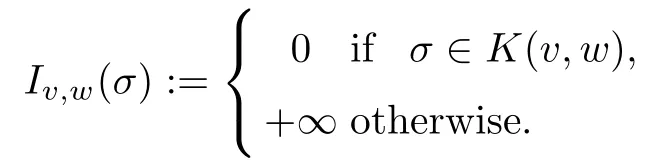
Its subdifferential has the form:

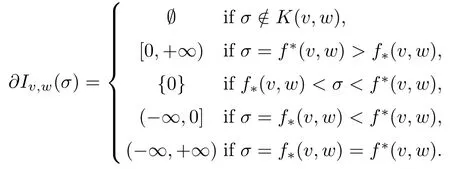
And，for μ＞0，the Yosida regularization of∂Iv，w(σ) is the function

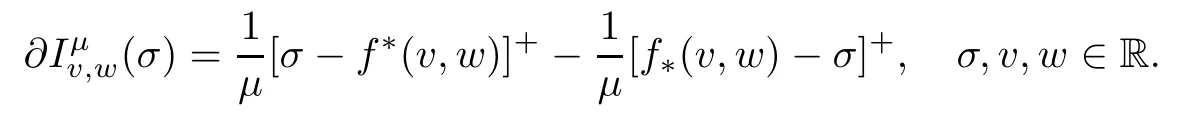
Let H be a Hilbert space with the norm|·|H.

Lemma 2.1Let vn→v，wn→w，σn→σ in L2(0，T;H)，fn→f weakly in L2(0，T;H).In addition，assume that a set-valued function K:H×H→cb (H) has convex values and

vi，wi∈H，i=1，2，where R＞0 is a constant.If

then

f (t)∈∂IK (v (t)，w (t))(σ(t)) for a.e.t∈[0，T]，

where IK (v (t)，w (t))is the indicator function of the set K (v (t)，w (t))⊂H，t∈[0，T].

ProofFirst，we define on L2(0，T;H) the function

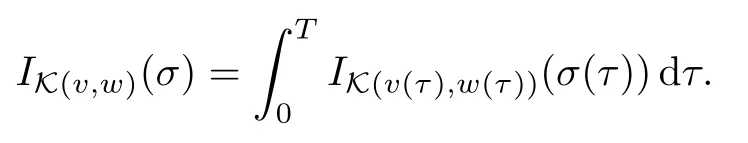
It is easy to see that IK (v，w)is the indicator function of the set

K (v，w)={σ∈L2(0，T;H);σ(t)∈K (v (t)，w (t)) a.e.on[0，T]}

and it is proper，convex，and lower semicontinuous.Moreover，[31，Proposition 0.3.3]implies that

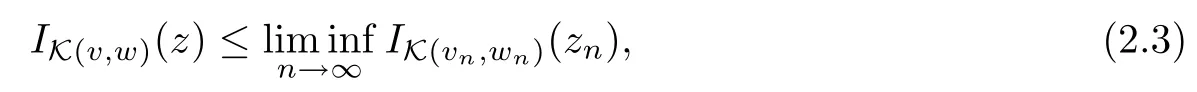
and for any z∈L2(0，T;H) there exists a sequence zn→z in L2(0，T;H) such that

So，let zn→z weakly in L2(0，T;H).In the case when=+∞，(2.3) trivially holds.Hence，without loss of generality，we can assume that=0，n≥1，which implies that zn∈K (vn，wn).Invoking the Mazur lemma from this inclusion and (2.1) we infer that

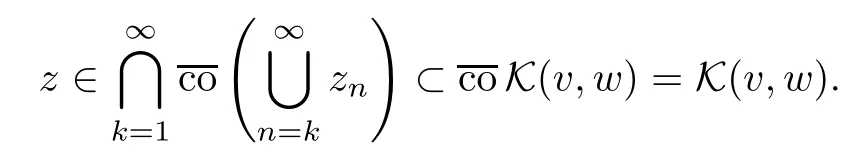
Therefore，IK (v，w)(z)=0 and (2.3) follows.

Take now an arbitrary z∈L2(0，T;H).When IK (v，w)(z)=+∞，(2.3) implies that (2.4) holds for any sequence zn→z in L2(0，T;H).Consequently，we assume that IK (v，w)(z)=0，i.e.z∈K (v，w).From (2.1) it follows that we can find a sequence zn→z in L2(0，T;H)，zn∈K (vn，wn).In this case，=0 and (2.4) holds again.

From (2.2) we deduce that σn∈=K (vn，wn)，i.e.=0.From the Mosco-convergence established above we obtain

Hence，σ∈domIK (v，w).Furthermore，for any z∈domIK (v，w)there exists a sequence zn∈，zn→z in L2(0，T;H) such that→IK (v，w)(z).The definition of the subdifferential together with (2.2) imply that

Passing to the limit in this inequality we obtain

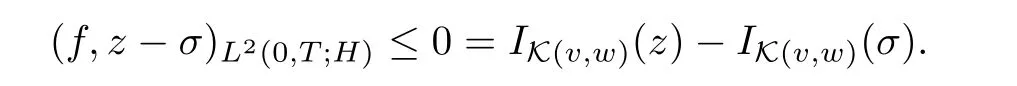
Since z∈domIK (v，w)is arbitrary，from this inequality it follows that

f∈∂IK (v，w)(σ).

The claim of the lemma finally follows from[31，Proposition 0.3.3]. □

In the rest of the paper，H denotes the Hilbert space L2(Ω) endowed with the standard inner product (·，·)Hand the associated norm|·|H，and V denotes the Sobolev space H1(Ω) equipped with the norm|v|V=，where (v，w)V=(v，w)H+a (v，w)，

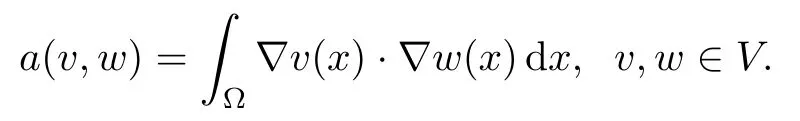
H2(Ω) is the Sobolev space W2，2(Ω).Consider the linear continuous operator L:V→V′defined by

〈Lv，w〉=a (v，w)，v，w∈V，

where V′is the dual space of V and〈·，·〉is the bilinear form establishing the duality between V and V′.Let-ΔN:D (-ΔN)⊂H→H denote the restriction of the operator L to the set of elements v∈V such that Lv∈H.Then，D (-ΔN)=and-ΔNv=-Δv for all v∈D (-ΔN).

Problem (P) is considered under the following hypotheses:

Hypotheses (H)The following assumptions hold throughout the paper:

(H1)κ＞0 is a given constant，λ∈C2(R) is a given function with λ′，λ′′bounded on R;

(H2) f*，f*∈C2(R2)∩W2，∞(R2) with 0≤f*≤f*≤1 on R2，and h (σ，0，w)=0 for σ∈[0，1]，w∈R，g (σ，v，0)=0 for σ∈[0，1]，v∈R;

(H3) F，h，g:R3→R are locally Lipschitz continuous functions;

(H4)σ0，v0，w0∈L∞(Ω)∩V with v0≥0，w0≥0 and f*(v0，w0)≤σ0≤f*(v0，w0) a.e.on Ω.

We note that the bounds for f*and f*in (H2) are justified from the biological point of view.Indeed，when the prey population v is zero，the vegetation σ in our three-species model stays constant，say it is one，after rescaling.And if v reaches some excessive number，then all the vegetation is devoured.So，we may assume that σ=0 in this case.

Denote by R+:=[0，+∞).In connection with the constraint (1.6)，we assume the following:

Hypotheses (U)The multivalued mapping U:[0，T]×Ω×R3→cb (R) has the following properties:

(U1) the mapping (t，x)→U (t，x，σ，v，w)，σ，v，w∈R，is measurable;

(U2) there exists k∈L2(0，T;R+) such that

hausR(U (t，x，σ1，v1，w1)，U (t，x，σ2，v2，w2))≤k (t)(|σ1-σ2|+|v1-v2|+|w1-w2|)

a.e.on Q (T)，σi，vi，wi∈R，i=1，2;

(U3) there exists a constant m＞0 such that

|U (t，x，σ，v，w)|≤ma.e.on Q (T)，σ，v，w∈R.

The last set of hypotheses lists the assumptions we impose on the cost integrand:

Hypotheses (q)The function q:ΩT×R3×R→R is such that

(q2) there exist k0∈L2(Q (T);R+) such that

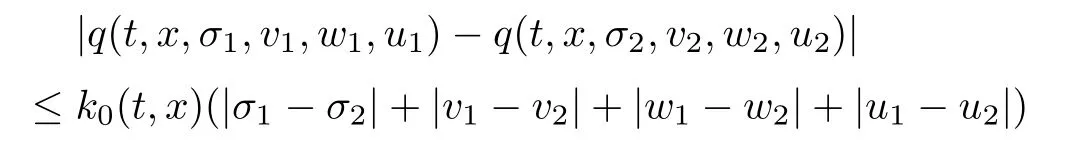
a.e.on Q (T)，σi，vi，wi∈R，|ui|≤m，i=1，2;

(q3) there exist functions ki∈L1(Q (T);R+)，i=1，2，k3∈L2(Q (T);R+) such that

|q (t，x，σ，v，w，u)|≤k1(t，x)+k2(t，x)|u|+k3(t，x)(|σ|+|v|+|w|)

a.e.on ΩT，σ，v，w∈R，|u|≤m.

Next，we reformulate our problem (P) in a function spaces framework.To this end，define the multivalued mapping

U (t，σ，v，w)={u∈H;u (x)∈U (t，x，σ(x)，v (x)，w (x)) a.e.on Ω}，σ，v，w∈H，

the function

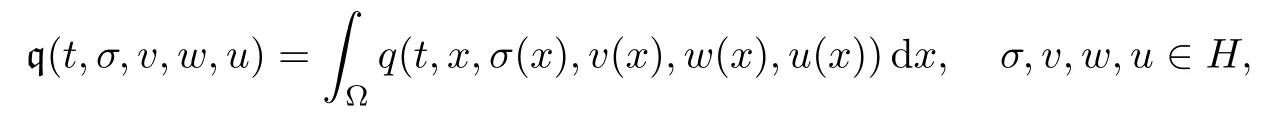
and the set

K (v，w)={σ∈H;f*(v (x)，w (x))≤σ(x)≤f*(v (x)，w (x)) a.e.on Ω}，v，w∈H，

Theorem 1.5 in[32]implies that

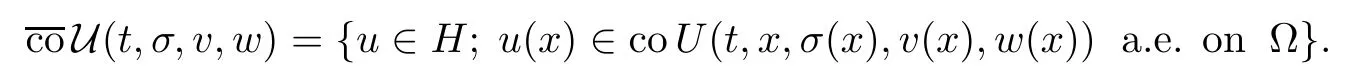
Given Hypotheses (U) and (q) it is a routine matter to verify (cf.，e.g.，[7，Lemmas 3.1 and 3.2]) that the mapping U:[0，T]×H3→cb (H) has the properties:

(U2) hausH(U (t，σ1，v1，w1)，U (t，σ2，v2，w2))≤k (t)(|σ1-σ2|H+|v1-v2|H+|w1-w2|H) a.e.on[0，T]，σi，vi，wi∈H，i=1，2，for k∈L2(0，T;R+) as above;

(U3)|U (t，σ，v，w)|H≤mμ(Ω)1/2a.e.on[0，T]，σ，v，w∈H，where m＞0 is as above and μ(Ω) is the Lebesgue measure of Ω，and the function q:[0，T]×H3×H→R has the properties:

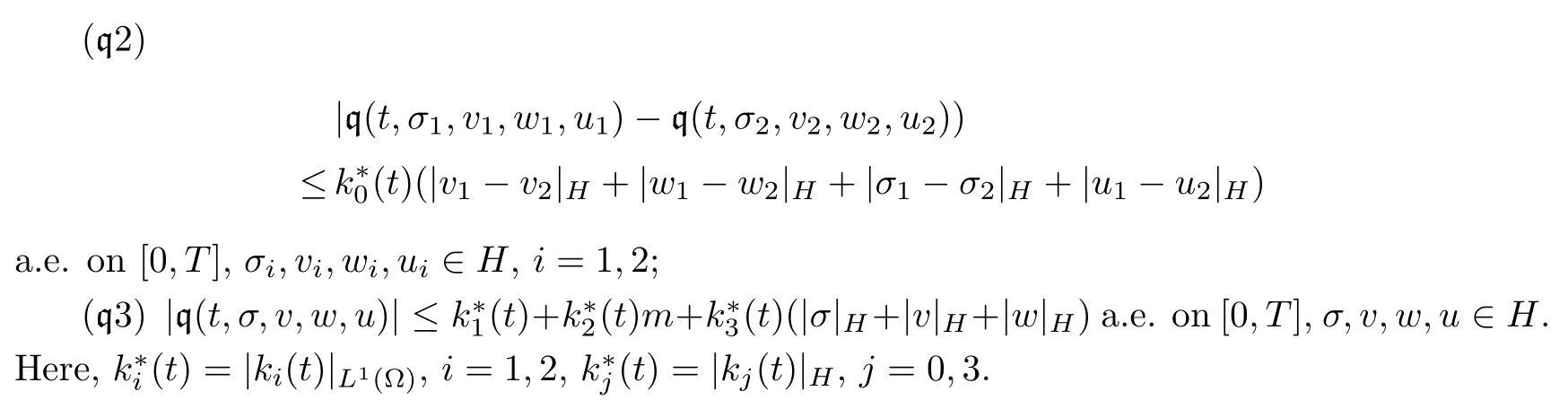
Let∂IK (v，w)(σ) be the subdifferential of the indicator function of K (v，w) at a point σ∈H.Now we are in a position to define solutions for our control problems.

Definition 2.2A quadruple{σ，v，w，u}is called a solution of control system (1.1)-(1.6) if

(i)σ，v，w∈W1，2(0，T;H)∩L∞(0，T;V)∩L2(0，T;H2(Ω));

(ii) u∈L2(0，T;H);

(iii)σ′-(λ(v))′-κΔNσ+∂IK (v，w)(σ)∋F (σ，v，w) uin H a.e.on[0，T];

(iv) v′-ΔNv=h (σ，v，w) in H a.e.on[0，T];

(v) w′-ΔNw=g (σ，v，w) in H a.e.on[0，T];

(vi)σ(0)=σ0，v (0)=v0，w (0)=w0in H;

(vii) u (t)∈U (t，v (t)，w (t)，σ(t)) in H a.e.on[0，T]，where the prime denotes derivative with respect to t.

A solution of control system (1.1)-(1.5)，(1.7) is defined similarly replacing the last inclusion with

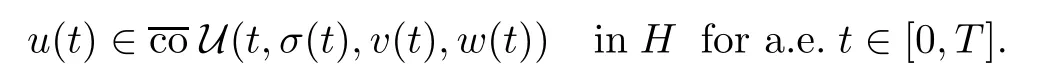
The sets of all solutions to control systems (1.1)-(1.6) and (1.1)-(1.5)，(1.7) in the sense of Definition 2.1 we denote by RUand，respectively.

Defining the function qU:[0，T]×H3×H→R∪{+∞}by the rule

So，our optimal control problems (P) and (RP) can now be reformulated in the form:

Given Hypotheses (H)，(U)，and (q)，the main purpose of this work is to prove the following results.

Theorem 2.3For any (σ*，v*，w*，u*)∈there exists a sequence (σn，vn，wn，un)∈RU，n≥1，such that

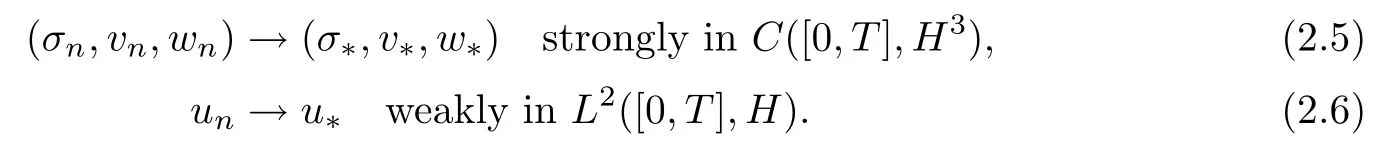
Moreover，

Theorem 2.4Problem (RP) has an optimal solution and

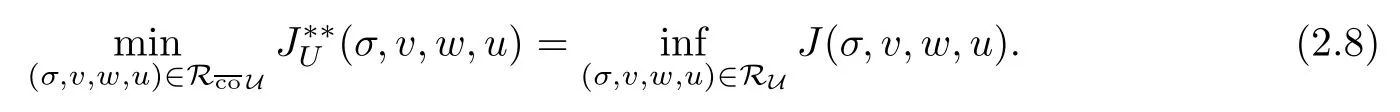
Moreover，for any solution (σ*，v*，w*，u*) of (RP) there exists a minimizing sequence (σn，vn，wn，un)∈RU，n≥1，for problem (P) such that (2.5)-(2.7) hold.

3 Properties of the Control-to-state Solution Operator

In this section，we define the control-to-state solution operator for our control systems and explore some of its properties which are crucial for establishing our main results in the next section.To this aim，first we let

Sm:={u∈L2(0，T;H);|u (t，x)|≤ma.e.on Q (T)}.

Due to convexity，the bound for the control functions of problem (P) given in Hypothesis (U3) obviously extends to the control functions of the convexified problem (RP).In particular，the controls of both problems belong to the set Sm.Accordingly，let T:Sm→C ([0，T];H×H×H) be the operator which with each u∈Smassociates the unique solution of system (1.1)-(1.5):

The existence and uniqueness of such a solution as well as uniform a priori estimates for all possible solutions independent of the control u are provided by the following theorem.

Theorem 3.1For any fixed u∈Smsystem (1.1)-(1.5) has a unique solution.Moreover，for any solution (v，w，σ) of (1.1)-(1.5) with u∈Smthe following estimates

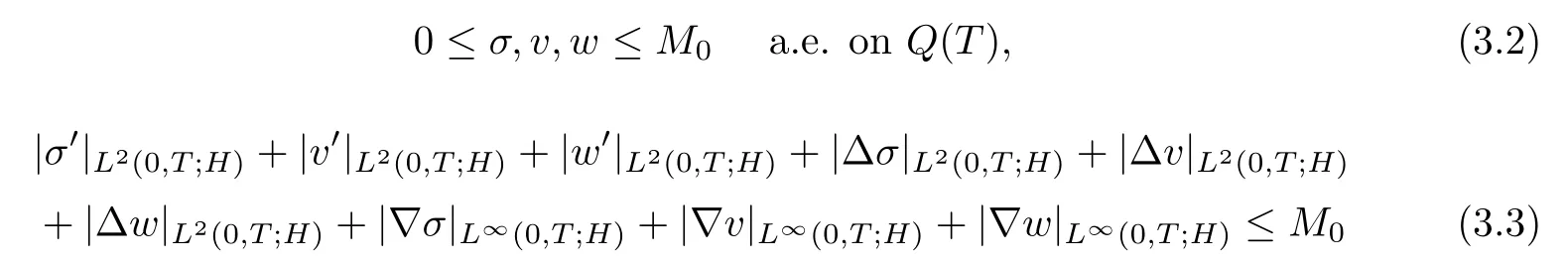
hold for a constant M0＞0 independent of u.

ProofThe existence of a unique solution to (1.1)-(1.5) with a fixed u∈Smand the estimate (3.2) can be proved following the pattern of[23，Theorems 3.1，3.2，and 3.10].

By virtue of the bound (3.2)，we may now assume (cutting offoutside the set where σ，v，and w are bounded，if necessary) that the functions F，h，g are all bounded (with a common bound M＞0) and globally Lipschitz continuous (with a common Lipschitz constant L＞1).

Below，we recap a part of the reasoning of[23]which will allow us to establish the uniform energy estimates (3.3).To this end，given μ＞0 we introduce the following approximate system:

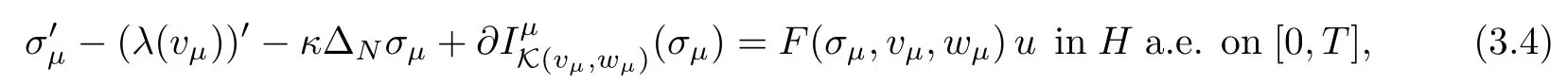
Here，for μ＞0 and σ，v，w∈R the functionis the Yosida regularization of the subdifferential∂IK (v，w)(σ).

By[23]，for any μ＞0 there exists a unique triplet (σμ，vμ，wμ) solving the approximate system above and satisfying the initial conditions σμ(0)=σ0，vμ(0)=v0，wμ(0)=w0.Arguing similarly to[23，3.3.2.proof of Theorem 3.6]we obtain the following counterparts of the inequalities (21)，(22)，(23)，(32) of this reference for such triplets (σμ，vμ，wμ)，μ＞0:

where C4=C1+ε1C1+ε2C2.Integrating this inequality from 0 to t∈(0，T]and then estimating the term-ε3(λ′(vμ)∇vμ，∇σμ)Hin the resulting inequality as follows

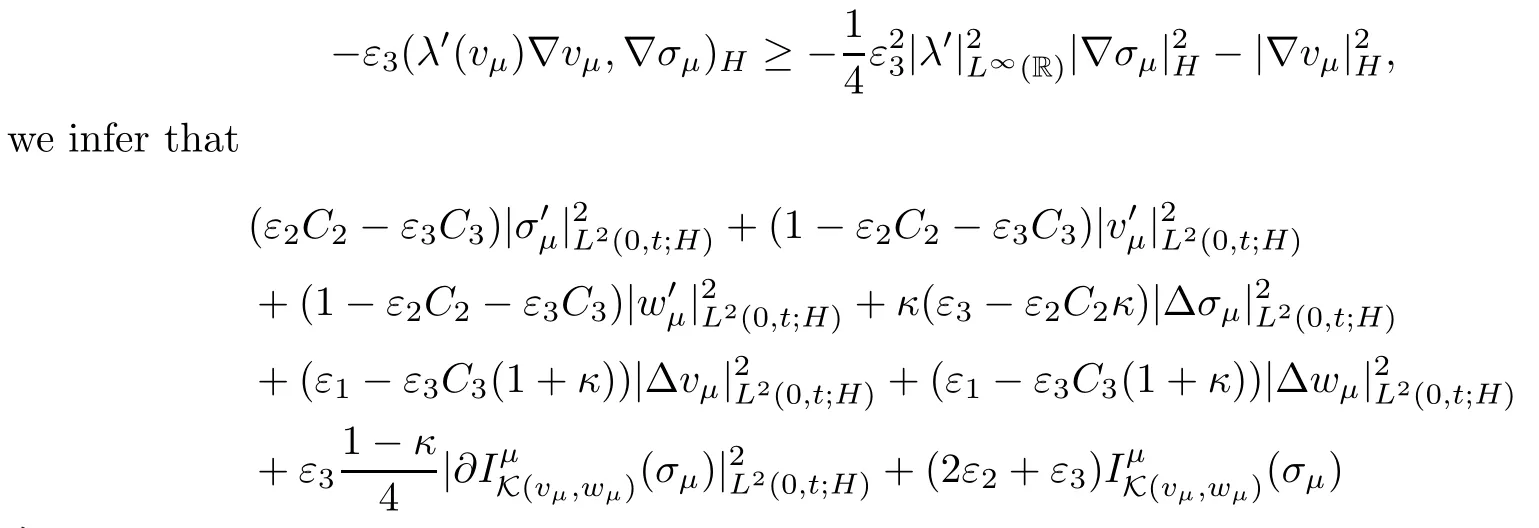
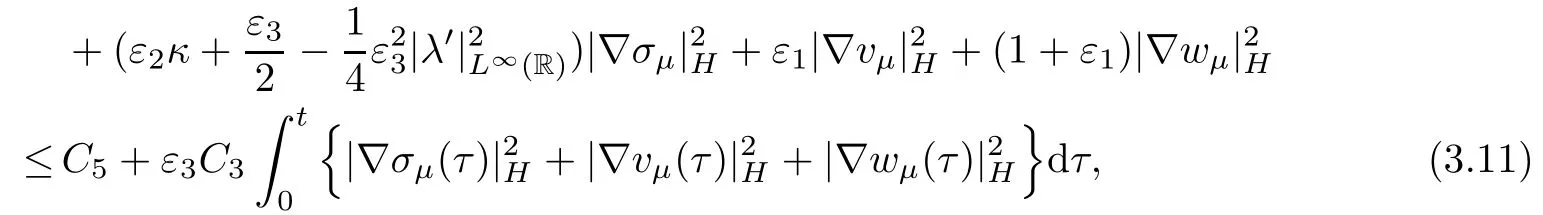
where C5is a positive constant which depends on|σ0|V，|v0|V，|w0|V，but is independent of μ.Now，all the coefficients in (3.11) will be positive provided we take

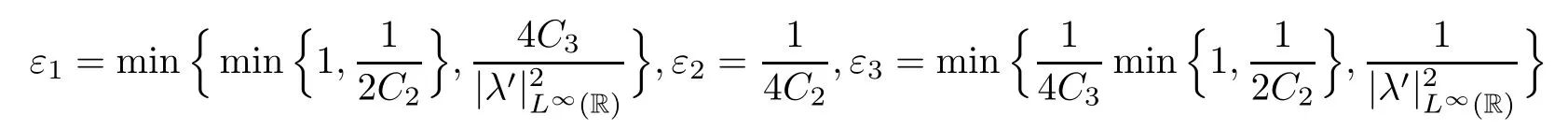
and choose κ∈(0，κ0) with

Therefore，invoking Gronwall’s inequality from (3.11) we obtain the following uniform energy estimates for the triplets (σμ，vμ，wμ)，μ＞0，solving the approximate problem (3.4)-(3.6):

By the weak and weak-star compactness results，this bound allows us to conclude that there exists a null sequence μn，n≥1，and functions σ，v，w∈W1，2(0，T;H)∩L∞(0，T;V)∩L2(0，T;H2(Ω)) such that

weakly in W1，2(0，T;H)∩L2(0，T;H2(Ω)) and weakly-star in L∞(0，T;V)，and，thus，strongly in C ([0，T];H).

With the convergences (3.13) at hand，we can now pass to the limit in eqs.(3.5)，(3.6) to infer that the triplet (σ，v，w) satisfies eqs.(iv)，(v) of Definition 2.1.Furthermore，denoting fn:=+(λ(vn))′+κΔNσn+F (σn，vn，wn) u we see that

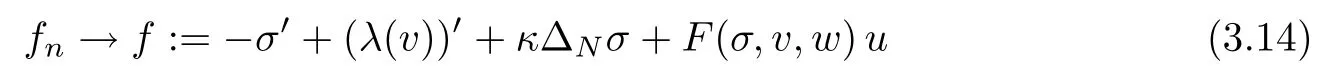
weakly in L2(0，T;H).Since[31，Proposition 0.3.5]

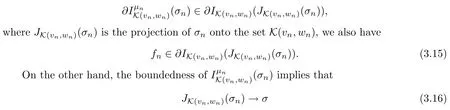
strongly in C ([0，T];H).In view of (3.13)-(3.16)，the application of Lemma 2.1 yields

f∈∂IK (v，w)(σ)，

so that the triplet (σ，v，w) satisfies eqs.(iii) of Definition 2.1 as well.We note that inequality (2.1) in this case follows from the Lipschitzness of f*and f*.Therefore，we conclude that(σ，v，w) is a solution of system (1.1)-(1.5) with a fixed u∈Sm.The estimate (3.3) now follows from (3.12) and (3.13). □

Theorem 3.2The operator T:Sm→C ([0，T];H×H×H) is weak-strong continuous.

ProofWe note that the set Smwhen endowed with the weak topology of the space L2(0，T;H) is metrizable.Consequently，to prove the theorem it is enough to show the sequential continuity of the operator T.Let，then，un，n≥1，be an arbitrary sequence from Smweakly converging to some u∈Sm.Denote by (σn，vn，wn):=(σ(un)，v (un)，w (un))，n≥1，the sequences of solutions to system (1.1)-(1.5) corresponding to the controls un，n≥1.Similarly as in the proof of Theorem 3.1，by the weak and weak-star compactness results，the uniform estimates (3.2) and (3.3) imply that there exists a subsequence (σk，vk，wk):=，k≥1，of the sequence (σn，vn，wn)，n≥1，and some functions σ，v，w∈W1，2(0，T;H)∩L∞(0，T;V)∩L2(0，T;H2(Ω)) such that

weakly in W1，2(0，T;H)∩L2(0，T;H2(Ω)) and weakly-star in L∞(0，T;V)，and，thus，strongly in C ([0，T];H).

From the Lipschitz continuity of the functions F，g，h and (3.17) we deduce that

weakly in L2([0，T];H) and

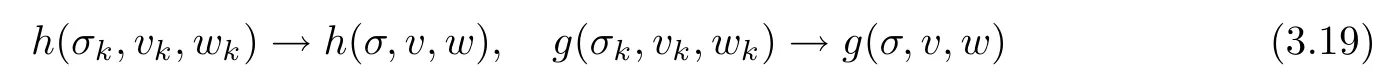
strongly in C ([0，T];H).The claim of the theorem now follows from the convergences (3.17)-(3.19) and Lemma 2.1. □

Theorem 3.3([26，Theorem 3.2]) Let ui∈Smand{σi，vi，wi}=T (ui)，i=1，2.Then，

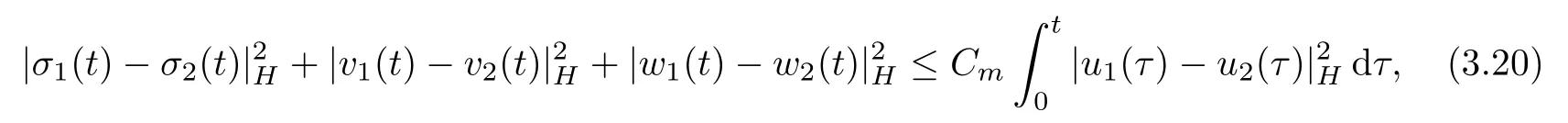
t∈[0，T]，where Cm＞0 is a positive constant depending only on m.

4 Proofs of the Main Results

In this section，we prove Theorems 2.1 and 2.2.To this end，first，on the basis of the control constraint multivalued mapping U and the cost integrand q we construct an auxiliary multivalued mapping Uq:[0，T]×H3→H×R as follows

where the Banach space H×R is equipped with the norm

Given the properties (U1)-(U3) and (q1)-(q3) we can easily show that the mapping Uqis measurable in t，continuous in the Hausdorffmetric on the space cb (H×R) in (σ，v，w) a.e.on[0，T]and

Moreover，we have (cf.[33，Lemma 2.2])

and for any ε＞0，there is a closed set Tε⊂[0，T]，μ([0，T]Tε)≤ε，such thatrestricted to Tε×H3×H is lower semicontinuous.This implies，in particular，that given an arbitrary (σ*，v*，w*，u*)∈，the function t→is measurable and

a.e.on[0，T].Since the bound in (4.3) evidently extends to，invoking[34，Corollary 1.1]，from the last inclusion we obtain the existence of a measurable function γn(t)∈U (t，σ*(t)，v*(t)，w*(t)) which，in view of (4.2)，satisfies

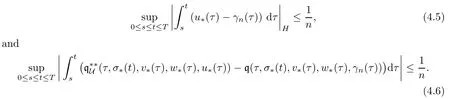
From Theorem 3.2 it follows that the set

R:={(σ，v，w)∈C ([0，T];H3);(σ，v，w)=T (u)，u∈Sm}

is compact in C ([0，T];H3).Fix n≥1.The property (U2) implies that for any (σ，v，w)∈H3and a.e.t∈[0，T]there exists γ∈U (t，σ，v，w) such that

Define the multivalued mapping

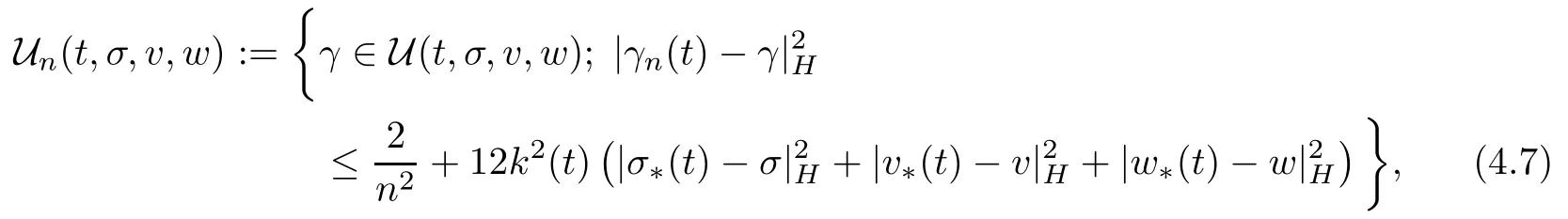
and the associated Nemytskii multivalued operator Γn:R→L2(0，T;H):

which is lower semicontinuous with nonempty closed decomposable values.According to[35，Theorem 3.1]there exists a continuous mapping αn:R→L1(0，T;H) such that

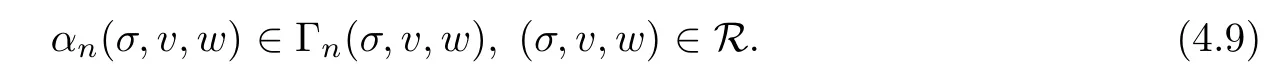
In view of the property (U3) and the definition of Un，from this inclusion we deduce that αnis continuous from R to L2(0，T;H) as well and αn(σ，v，w)∈Sm，(σ，v，w)∈R.

Consider now the superposition of T and αn.By virtue of Theorem 3.2 it follows that this superposition αn°T:Sm→Smis weak-weak continuous.Since Smis obviously convex and compact in the weak topology of the space L2(0，T;H)，from the Schauder fixed point theorem it follows that there exists a fixed point un∈Smof the operator αn°T，i.e.，

Setting (σn，vn，wn):=T (un)，from (4.7)-(4.10) we see that (σn，vn，wn，un)∈RU，n≥1，and

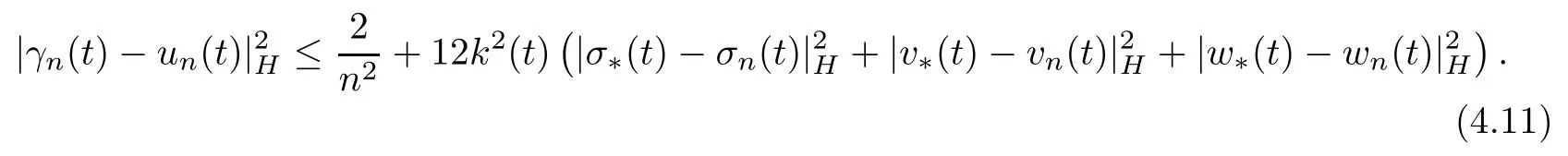
Since on the set Smthe topology induced by the“weak”norm in (4.5) coincides with the weak topology of the space L2(0，T;H)，from (4.5) we obtain

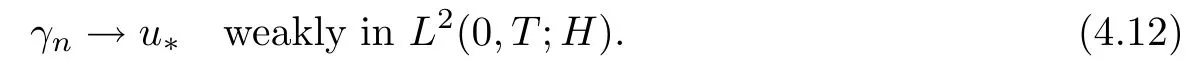
Theorem 3.2 implies then that

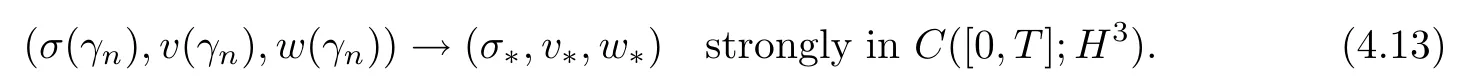
From (4.11) and (3.20) it follows that

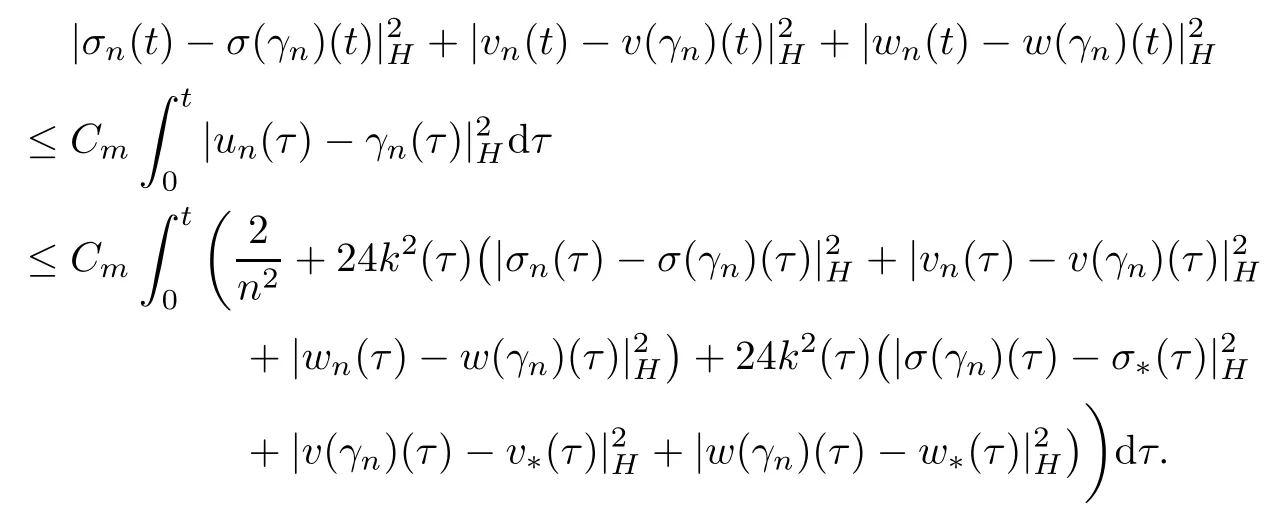
Invoking Gronwall’s lemma，from the last inequality and (4.13) we obtain

(σn，vn，wn)→(σ*，v*，w*) strongly in C ([0，T];H3).

Finally，from (4.11)，(4.12)，and Lebesgue’s dominated convergence theorem we conclude that

un→u*weakly in L2(0，T;H)，

and the claim of Theorem 2.1 follows.

Set now R:={(σ(t)，v (t)，w (t));t∈[0，T]，(σ，v，w)∈RU}.Theorem 3.2 together with Hypothesis (U3) imply that the set R is compact in H3.Define φ:[0，T]×H3×H→R∪{+∞}by

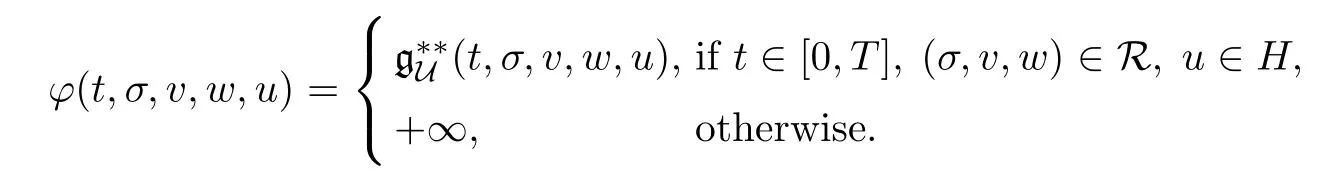
-l (t)≤q (t，σ，v，w，u) for a.e.t∈[0，T]，σ，v，w，u∈H，

for some l∈L1([0，T]，R+).

De fining now the integral functional

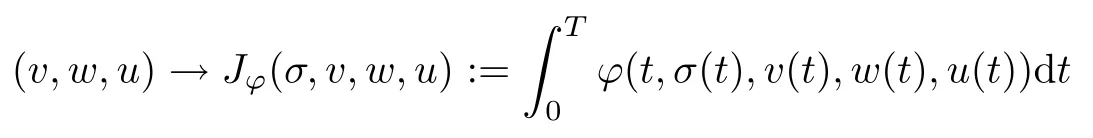
from[36，Theorem 2.1]we deduce that Jφis sequentially lower semicontinuous on the space C ([0，T]，H3)×L2([0，T]，H)，when L2([0，T]，H) is endowed with the weak topology.According to Theorem 3.2 the setis compact in this space.Since，obviously，Jφ(σ，v，w，u)=，we conclude that problem (RP) has a solution (σ*，v*，w*，u*)∈.Then，Theorem 2.1 implies that there exists a sequence (σn，vn，wn，un)∈RU，n≥1，such that (2.5)-(2.7) hold.In particular，

which combined with

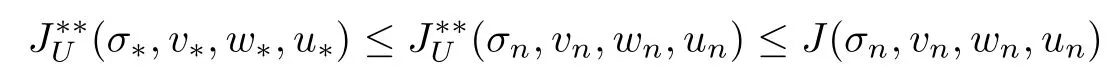
proves Theorem 2.2.