Holographic Entanglement Entropy: A Topical Review∗

Bin Chen (陈斌)

1Department of Physics and State Key Laboratory of Nuclear Physics and Technology,Peking University,5 Yiheyuan Rd,Beijing 100871,China

2Collaborative Innovation Center of Quantum Matter,5 Yiheyuan Rd,Beijing 100871,China

3Center for High Energy Physics,Peking University,5 Yiheyuan Rd,Beijing 100871,China

Abstract In this topic review,we introduce recent developments on holographic entanglement entropy.After briefly reviewing the basic notions of entanglement in quantum information and quantum field theory,we introduce the Ryu-Takayanagi’s prescription of computing the entanglement entropy holographically.We review the inequalities on the holographic entanglement entropy,and its derivation from Euclidean gravity.In particular,we discuss its implications in semi-classical AdS3/CFT2correspondence,and furthermore review the recent studies on the emergence of geometry and gravity from entanglement.

Key words: entanglement entropy,gravity,holography,AdS-CFT correspondence

1 Introduction

Holographic entanglement entropy (HEE) is at the intersection of quantum gravity,quantum field theory and quantum information.Since its proposal in 2006 by Ryu and Takayanagi,[1−3]it has been intensely investigated from various angles,and its study has shed new lights on the AdS/CFT correspondence,black hole physics,and quantum many-body systems.

Entanglement is a fundamental feature in quantum world.For example,consider a system of two spin-1/2 particle.If the wavefunction of the system is just the product of wavefunctions of individual particles

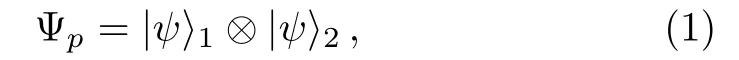
the two particle is not entangled.On the contrary,if the wavefunction of the system cannot be factorized into the product of the wavefunctions of two particles,like the wellknown EPR state,

then the two particles are entangled.

Entanglement entropy measures how much a given quantum state is entangled.It can be defined as follows.[4−5]One can divide a system into two parts,sayAand its complementAc.If the system is of finite degrees of freedom,the Hilbert space of the whole system is the tensor product of the ones ofAandAc.Given a stateof the whole system,the density matrixρof the system isρ=One may obtain the reduced density matrix ofAby tracing over the degrees of freedom ofAc,i.e.ρA=TrAcρ.Then the entanglement entropy ofAandBis defined as

More generally one can define the Rényi entropy ofAandAcas

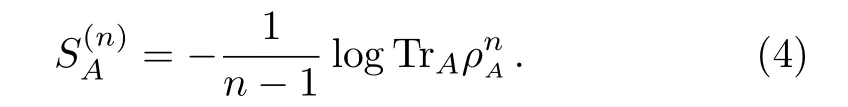
The entanglement entropy and the Rényi entropy are related by

Moreover one may choose two subsystemsAandB,which are not necessarily complementary to each other,and define the Rényi mutual information ofAandB

The mutual informationencodes the entanglement betweenAandB.We will review the properties of the entanglement entropy in Sec.2.For a nice review on information theory,see Ref.[6].

The entanglement entropy in quantum field theory is much subtler.The difficulty comes from the fact that in a field theory there are infinite number of degrees of freedom.As shown in Refs.[7–9],for a quantum field,its von Neumann algebra is of type III,and its Hilbert space cannot be factorized.Strictly speaking in mathematical sense,one cannot define the trace or the density matrix for a QFT.‡Nevertheless we may overlook these subtleties and take the approximation that a QFT could be a continuous limit of a discrete system.Now we can choose a time slice and consider the system in a spacelike hypersurface,then formally we may define the entanglement entropy as in a quantum many body system.The standard way of computing the(Rényi)entanglement entropy is the replica trick,[11]but it is usually hard to operate for a general system.Some computations in 2D CFT and higher dimensional free field theory could be found in Refs.[12–18].We will discuss briefly the entanglement entropy in QFT in Sec.3.

For a CFT with a gravity dual one may use the AdS/CFT correspondence[19−21]to do a simpler holographic computation in the bulk gravity.For the pure AdS gravity,it was conjectured by Ryu and Takayanagi that the leading contribution of entanglement entropy is captured by the area of a minimal surface in the bulk with asymptotic boundary ending onA.[1−2]The proposal was further generalized to the stationary case,leading to the Hubeny-Rangamani-Takayanagi (HRT)prescription.[3]The so-called Ryu-Takayanagi (RT) area law is reminiscent of the black hole entropy,and therefore since its proposal there have been many attempts to derive this law in the gravity.In Ref.[22],the holographic entanglement entropy was shown to be a kind of generalized gravitational entropy.In Sec.4,we will review the holographic entanglement entropy and its derivation.For nice reviews on HEE,see Refs.[23–26].

The HEE has various implications on the AdS/CFT correspondence.In this topical review,we would like to introduce three topics: semiclassical AdS3/CFT2correspondence,geometry from entanglement and gravity from entanglement.As HEE could be taken as a gravitational entropy,its study sheds new light on the semi-classical quantum gravity.In particular,in the context of AdS3/CFT2correspondence,the study of the entanglement entropy of double-interval and single-interval on a torus inspired people to investigate the gravity beyond classical level.In Sec.5,we review the Rényi entropy in holographic CFT and its implications on semi-classical AdS3gravity.

The HEE opens a new window to study the holographic principle of quantum gravity.The emergence of the extremal surface corresponding to the boundary subregion suggests a deep relation between geometry and entanglement.It is in accord with J.Wheeler’s idea “It from qubit”.There are many efforts to understand how the geometry and gravitational dynamics emerge from entanglement.We will review some of them in Sec.6.

This brief review is far from complete.It reflects the author’s biased view on the subject.We omit lots of interesting studies.And we are not going after the completeness of the references.For a complete list of the references,please refer to the wonderful book[25]by M.Rangamani and T.Takayanagi.

2 Entanglement Entropy

Let us start from the Shannon entropy in classical information theory.Consider a string of symbolsaandb,

We assume that the letteraoccurs with probabilityPand the letterboccurs with probability 1−P,then in a string of lengthNthe letteraappearsPNtimes while the letterbappears (1−P)Ntimes.The number of bits of information of the message of the lengthNwithN ≫1 isNS,whereSis the Shanon entropy per letter

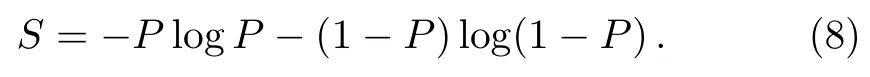
More generally,we haveklettersa1,a2,...,ak,each one appearing in the message with probabilityP1,P2,...,Pkrespectively,with∑=1,then the Shannon entropy is

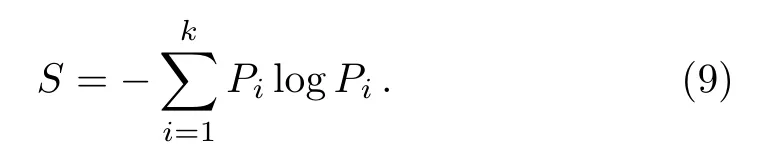
In quantum mechanics,we may replace the classical probability distributionPiwith the density matrix.Let us consider a bipartite systemAandB.The Hilbert space of the system isHAB=HA⊗HB.Assume that we have a pure state

with

Ifi=1,the state is a tensor product state,while ifi>1,the state ΨABis an entangled state.If we can only do measurement in subregionA,then the subsystem behaves with a reduced density matrix.For example,consider an operatorOAonA,its expectation value is

whereρAis the reduced density matrix obtained by tracing over the degrees of freedom ofB

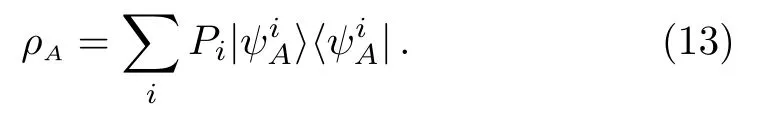
More generally,even if the state ΨABis not a pure state,we can still readρAby taking the partial trace

The entanglement entropy is defined by the von Neumann entropy

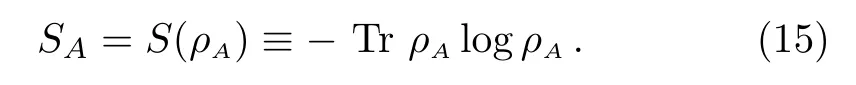
It measures how much for a given quantum state the subregionAis entangled with its environment.For the reduced density matrix (13),the entropy reads

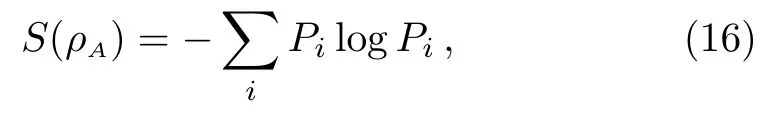
which is the same as the Shannon entropy (9) of a probability distribution{Pi}.It is easy to see thatS(ρA)≥0.For a pure state,there is alwaysS(ρA)=S(ρB).

For example,consider a two spin 1/2 system.If the wavefunction of the system is

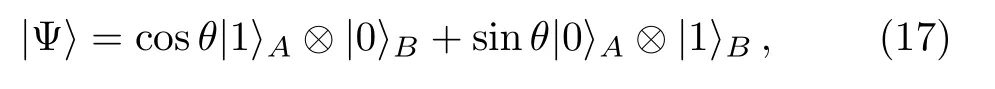
then the reduced density matrix forAis

The entanglement entropy is

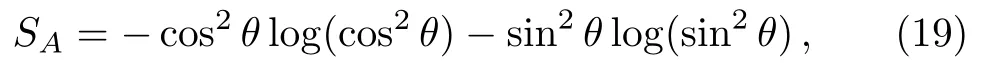
which is vanishing whenθ=0 orπ/2,and takes maximal valueSA=log 2 at cos2θ=1/2.

One important quantity in the study of the entanglement entropy is the relative entropy.Letρ,σbe two density matrices on the same Hilbert space,the relative entropy is defined to be

It is positive semi-definite

This property implies the subadditivity of the entanglement entropy.Consider two subsystemsAandBwhich could be not complement to each other,one can define the mutual information ofAandBas

The mutual information characterizes how much the two subsystem is entangled.It is positive semi-definite,which is referred to as the subadditivity of the entropy.To show this point,one may define two density matricesρABandσAB=ρA⊗ρB,then one finds

Another important inequality is the so-called Araki-Lieb inequality,[27]which states that

IfAandBare complement to each other and the system is in a pure state,thenSA=SB.More generally,the inequality bounds the difference of the entanglement entropies of a subsystem and its complement in terms of that of the whole system.With the subadditivity,one has

The relative entropy is monotonic in the sense that once we shrink the subsystem the relative entropy decreases accordingly.Consider a bipartite systemABwith two density matricesρABandσAB,from which we can get the reduced density matrices

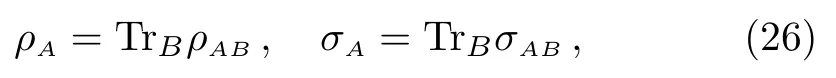
then we have

This means that taking a partial trace can only reduce the relative entropy.From the monitonicity of relative entropy we can get the strong subadditivity of the entanglement entropy.From a tripartite systemABCwith a density matrixρABC,we have

Let us introduce another density matrixσABC=ρA⊗ρBC,and we have

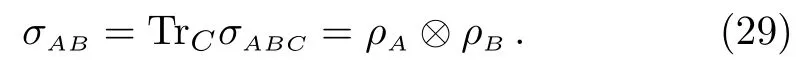
From monotonicity,we have

This leads to strong subadditivity

The entanglement entropy has been intensely studied in the quantum many-body systems,even though it is hard to be observed directly.It has been computed numerically in spin chains,lattice models etc.It encodes valuable information of the system,say the dynamical degrees of freedom in 2D systems.It has various physical applications,including as the quantum order parameter in condensed matter system,[28−29]characterizing the non-equilibrium states,etc.In the past decade,the entanglement entropy establishes a bridge between gravity and QFT,in particular CFT,and provides a new window to study AdS/CFT correspondence.

3 Entanglement Entropy in QFT

Consider a relativistic quantum field theory (QFT)on some Lorentzian spacetimeBd,which we take to be Minknowski spacetimeR1,d−1.We may choose a Cauchy surface Σd−1,being achronal spacelike slice.In the surface Σd−1,consider a submanifoldAand define the entanglement entropy as before,but now the wavefunction is replaced with a wavefunctional Ψ(ϕ(x)),whereϕ(x) is the quantum field.More fundamentally,the vacuum of a QFT is highly entangled.It is difficult to compute the entanglement entropy in a QFT,which has infinite number of degrees of freedom,§For nice reviews on the entanglement entropy in free field theory and conformal field theory,see Refs.[13,15].even after we take the point of view that the field theory can be discretized such that the Hilbert space can be factorizedH=HA⊗HAc,whereAcis the complement ofAin Σ.Instead of working with the entanglement entropy,it is better to compute first the Rényi entropy=[1/(1−n)]log TrHA(ρnA),and then take then →1 limit to readSA.The Rényi entropy encodes the finer information on the entanglement.It probes the purity of the system.For example,if the state is a mixed state,one has≠0.Moreover,once the tower of all the Rényi entropies is known,the detailed information on the reduced density matrix is known.In the vacuum,there is always=

One can introduce the modular Hamiltonian by rewriting

whereKAis called the modular Hamiltonian.Usually,KAis nonlocal.But in the case of half plane,KAhas a local form.From the Rényi entropy,one may define modular entropy:

In terms of the modular Hamiltonian,the Rényi entropy reads

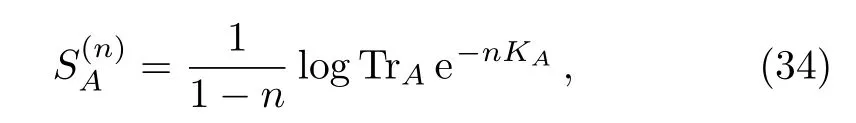
which could be taken as the modular free energy at the temperatureT=1/n.In quantum statistical mechanics,we have the free energy

and the entropy is

Similarly we have the modular entropy

Consider the relative entropy,which could be recast into the form

Choosing the density matrices

then up to the linear order ofϵ,we have

which is called the first law of entanglement.It is suggestive to compare it to the first law of thermodynamics dE=TdS.This law may lead to the linearized Einstein equation in the context of holographic entanglement entropy,as we will show later.To the quadratic order ofϵ,we get

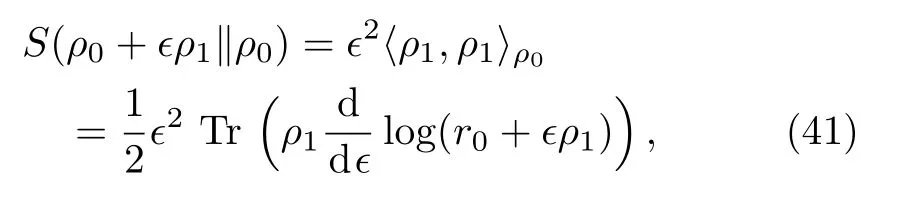
whereis known as the quantum Fisher information.Due to the positivity of the relative entropy,the quantum Fisher information is non-degenerate,positivedefinite and symmetric.It can be taken as a Riemannian metric on the space of states.

The entanglement entropy in QFT obeys the area law.[30−32]More precisely,for a local QFT ind ≥3,the leading order entanglement entropy takes a universal form

where∂Ais the boundary of entangling surface andϵis the UV cutoff.The factorγdepends on the details of the QFT.The area law suggests that the entanglement betweenAand its environment occurs most strongly at the boundary,originating from the EPR pairs across the entangling surface.The area law holds for both ground states and finite temperature systems,but is violated for highly excited states.For a nonlocal QFT,the area law could break down as well.It has been proven rigorously for free field theories.Moreover,in a 2D QFT,due to the important IR effect,the entanglement entropy is of logarithmic behavior.Besides the leading order contributions,the entanglement entropy has other subleading contributions.Suppose the typical scale of the subregionAis of sizeL,then the entanglement entropy ofAis of typical form

The remarkable fact is the coefficientUAis universal and is related to the Weyl anomaly.This helps us to understand the renormalization group flow.[33−35]

To compute the entanglement entropy,one may use the replica trick to compute TrρnAfirst.Let us fix the Cauchy surface to be Σ=Σt=0.For a quantum fieldϕ(x),we have

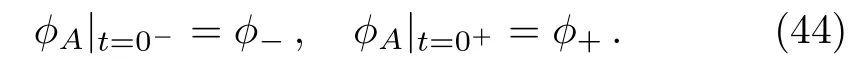
In the path-integral formalism,the reduced density matrix is and then-th power of the reduced density matrix is

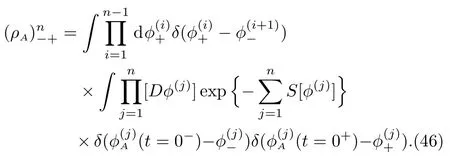
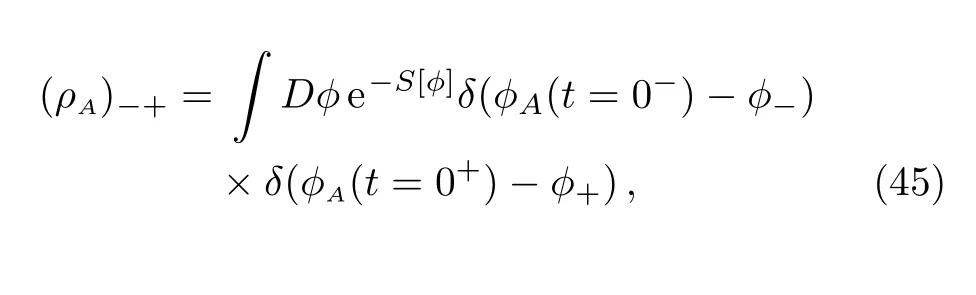
In the above,ρAis computed on a copy of the background spacetime,andρnAis computed onncopies of such manifold.The first line in Eq.(46)shows that one has to identify the field configurations in two adjacent copies along the entangling surfaceA.Taking the trace ofρnA,we find a partition function on ann-folded manifoldBn

This partition function could be understood either as the one ofn-copied theory with field identification,or the one of original theory on ann-folded manifoldBn.Considering the normalization,we have

In the above path integral,there is a cyclic permutation symmetry amongst the various copies of the functional integral.ThisZnsymmetry is referred to as the replica symmetry.

To compute the entanglement entropy it requires takingn →1 limit.Such a limit is not always well-defined.One has to do analytic continuation by lettingnto be a real number.This is feasible if the function satisfies the requirement of Carlson’s theorem.¶Carlson’s theorem: the function defined on integers,which in addition are well-behaved as z →±i∞,allows for a unique analytic continuation away from integers.

The field identification between adjacent replica

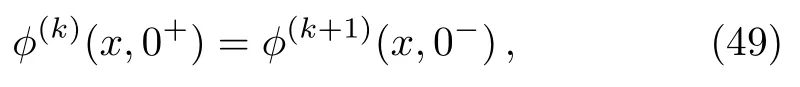
can be equivalently implemented by introducing a twist field on the entangling surface.The twist operatorTis an operator of codimension two,usually is nonlocal.The partition function onBncan be computed either byZ(Bn)or by the correlation function of the twist operators in a cyclic orbifold CFT

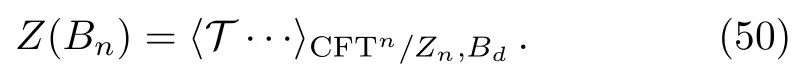
In the spacetime ofd ≥3,the manifoldBnis not only of singularity but also of nontrivial topology such that the partition function onBnis difficult to compute.In this case,the twist operatorTis nonlocal and its correlation function is hard to read as well.

In two-dimensional spacetime,the situation is much better.A twist operator in 2D CFT consists of two local operatorsσn,inserting at the branch points of an interval.The two local operators are called twist operators as well.They are primary operators of conformal dimension in the orbifold CFT

wherecis the central charge of original CFT.When the entangling surface is a single interval,one has

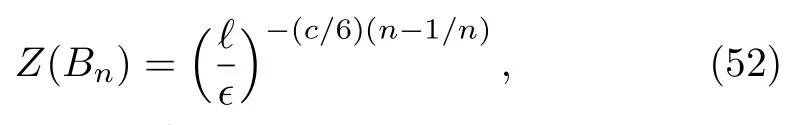
whereℓis the length of the interval andϵis the UV cutoff.This allows us to read the single-interval Rényi and entanglement entropies

These two formulae are of universal feature in the sense that they depend only on the central charge,independent of the details of the CFT.Via conformal mappings,one can read the single-interval entropy on a cylinder of sizeL

and the single-interval entropy in a thermal CFT

whereβis the period of the thermal direction.

For the multi-interval case,the computation becomes formidable even in two dimensional CFT.In the case ofNintervals,there are many branch cuts so that the Riemann surface is of genus (n −1)(N −1),wherenis the number of replica.The partition functions on a higher genus Riemann surface are only known for free bosons and fermions.If we have multiple intervalsA=[z1,z2]∪···∪[z2N−1,z2N],

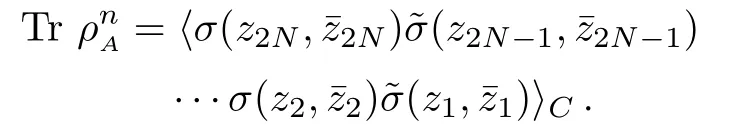
This is a multi-point function and hard to handle.Nevertheless,in the case that the intervals are short,we may use operator product expansion (OPE) of twist operators to do large distance expansion.Moreover,if we consider the holographic CFT,which has a large central charge,the above correlator could be much simplified,as the vacuum module dominates the contribution.[12,36−37]

It is remarkable that one can still apply the OPE of the twist operator to compute the mutual information of two disjoint spheres in the large distance regime in higher dimensions.[18]In particular,for a higher dimensional CFT,the first few leading order contribution to the mutual information is of universal feature,depending only on the conformal dimensions of the operators.[38−39]Such universal feature could be understood from holographical point of view.[38,40]

4 Holographic Entanglement Entropy

In 2006,Ryu and Takayanagi proposed that in the context of AdS/CFT,the entanglement entropy in CFT could be computed holographically in semiclassical gravity.The prescription is as follows.Consider a subregionAwith a boundary∂Ain the boundary CFT defined onBd,then find a co-dimension 2 extremal surfaceEAanchored on∂Ain the bulk manifoldMd+1

HereEAshould be homologous toA,which means thatEAcan be smoothly retracted toAor more precisely there is a co-dimension 1 homology subregionRd∈Md+1such that∂Rd=EA∪A.The holographic entanglement entropy ofAis given by the HRT formula[3]

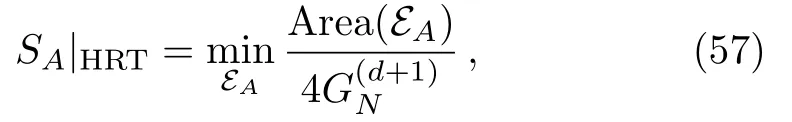
where among theEA’s satisfying the homology constraint one has to choose the one with minimal area.For the static case,the formula reduces to original Ryu-Takayanagi (RT) formula[1]

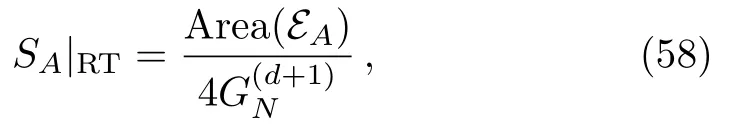
whereEAis the minimal surface.This relation is reminiscent of the Bekenstein-Hawking entropy for black hole in Einstein’s gravity.As we will show soon,this is due to the fact that the holographic entanglement entropy could be understood as a generalized gravitational entropy.

The extremal surfaceEAis a co-dimension two spacelike surface.It has a timelike and a spacelike normal,i.e.its normal bundle has a local Lorentzian structure ofR1,1.This allows us to construct two null normals(1)and(2)satisfying

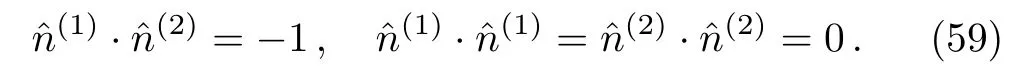
We may define a projector

from which we can write the extrinsic curvature tensors of the co-dimension two surface

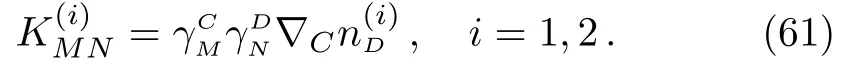
The surface is extremal means that the extrinsic curvatures of the null surface is vanishing

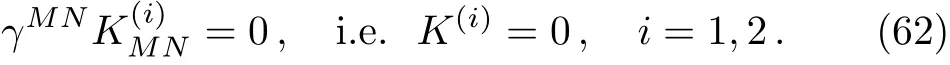
If the state in CFT is static,then we have the RT formula in which the extremal surfaceEshould be minimal.In this paper,we focus on the static case and consider the minimal surface in the bulk.

To apply the RT prescription,we start from the AdS metric in the Fefferman-Graham gauge:

wherezcharacterizes the radial direction.For the extremal surfaceEA,it is described by a set of functionsxM(ξi),whereξiare its intrinsic parameters.The induced metric onEAis

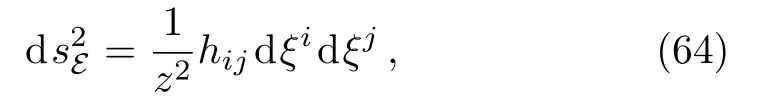
where

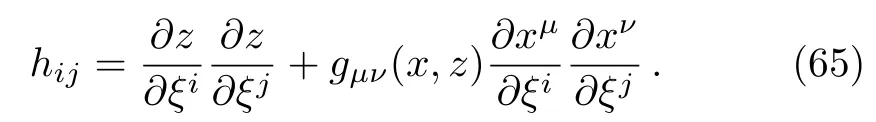
The RT formula reads

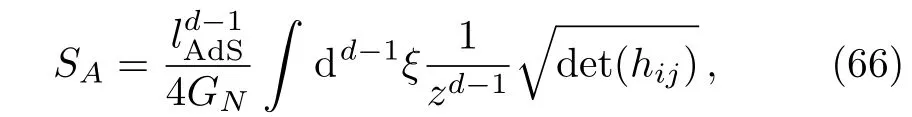
with the boundary condition

In general,given a boundary regionA,it is very difficult to find a minimal surface anchored on∂A.Nevertheless,if the regionAis of high symmetries,the problem to find the minimal surface can be solved.

4.1 Holographic Entanglement Entropy for 2D CFT

Let us consider 2D holographic CFT.In this case,according to AdS3/CFT2,we have

wherecis the central charge of 2D CFT,lis the AdS3radius,andGis three-dimensional Newton constant.The subregionAis composed of intervals.For a single interval case,A={x ∈R|x ∈(−ℓ/2,ℓ/2)},and the minimal surface is now the geodesic in AdS3ending on the branch points±ℓ/2.Now the holographic entanglement entropy is

The geodesic is now just a semi-circle of radiusℓ/2 parametrized by

As the integral in AdS3is divergent,we have to introduce an IR cutoff in radial directionz=ϵ,which corresponds to a UV cutoff in CFT,then we have

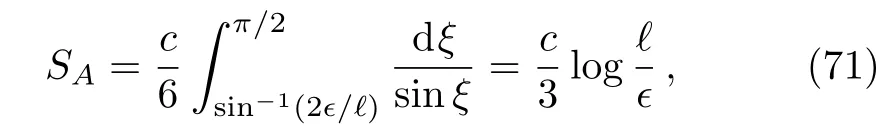
which agrees exactly with the field theory result.

For the multi-interval case,A=∪iAi,Ai={x ∈R|x ∈(ui,vi)}.For each interval,we have

The entropy for the whole regionAis subtler,as now there are more geodesics ending on the branch points.For example,for the double-interval case,besides one set of two geodesics connectinguiandvi,i=1,2,we have the other set of two other geodesics,one connectingv1andu2,and the other connectingu1andv2.Then we have to choose the set of geodesics of shorter length:

4.2 Holographic Entropy Inequalities

It is relatively easy to prove some inequalities for the holographic entanglement entropy.First of all it is positive and obeys the area law in a natural way.The subadditivity is a little subtle.For two regionsAandB,which are far apart,their holographic mutual information is zero.But in field theory,the mutual information satisfies[41]

whereOA,OBare the arbitrary observables in the regionsAandBrespectively.In other words,the mutual information for two disjoint regions are generally positive.The resolution of this conflict is that the holographic mutual information is related to the on-shell regularized gravity action.The nonvanishing mutual information suggests that one has to consider the gravity beyond the classical level.

The strong subadditivity of the holographic entanglement entropy in the static case could be easily shown in the case of 2D CFT.[42]In these cases,the HEE is read by the geodesic length such that the inequality can be proved straightforwardly.The study can be generalized to the higher dimensional CFT with the subregions being strips.For the time-dependent case,the strong subadditivity of the covariant HEE was proved in Ref.[43].

The holographic entanglement entropy obeys the Araki-Lieb inequality.Moreover it can saturate the bound.Consider a thermal state of CFTdonSd−1×R,which corresponds to a global Schwarzschild-AdSd+1black hole.The subsystemAis part ofSd−1.It was found that when the size ofAis large enough,the holographic entanglement entropy ofAcould have two potential contributions from:

(i) A single connected surfaceEAwhich is homologous toA.

(ii) A disconnected surface which consists of the surfaceEAchomologous toAcand the black hole horizon.

There exists a critical size beyond which the HEE ofAis captured by the contribution (ii) so that we have

which saturates the Araki-Lieb bound.This phenomenon is called the entanglement plateau.[44]

Besides the usual entropy inequalities,the holographic entanglement entropy actually obeys a few more inequalities,which are specific to holographic field theories in the semiclassic limit.The most famous one is the so-called monogamy of mutual information.Consider a tripartite information defined by

Monogamy of mutual information means thatI3should be non-positive definite,i.e.I3≤0.In simple quantum systems,the mutual information is not monogamous,for example,the GHZ state for four qubits.Nevertheless,the holographic mutual information is monogamous,as shown in Ref.[45]for the RT proposal and in Ref.[43]for the HRT proposal.Furthermore,the monogamy of holographic mutual information was generalized to other holographic inequalities,which could be encoded in the so-called holographic entropy cone.[46]The holographic entanglement entropy inequalities may help us to understand which states of a CFT could have a semi-classical gravitational duals.

4.3 Generalized Gravitational Entropy

The RT formula is reminiscent of the Bekenstein-Hawking entropy formula,which states that the black hole entropy is proportional to the area of the horizon.This inspired people to study the relation between the HEE and the black hole entropy.In Ref.[22],∥For the earlier effort on this issue,see Refs.[47–48].it was shown that the HEE for the static case could be understood as a generalized gravitational entropy in the framework of Euclidean gravity.The study on the time-dependent case was carried out in Ref.[49].The study has been generalized to the higher derivative gravities.[50−52]Here we only review the static case.

From the AdS/CFT correspondence,there could be an on-shell gravitational configurationMndual to thenreplicated geometryBnin boundary CFT,with∂Mn=Bn.The bulk partition function could be approximated by the on-shell regularized gravitational action

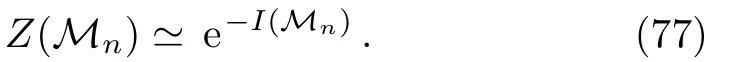
The bulk configurationMnis smooth,but it is hard to find explicitly.One important step is to take aZnquotient as well.Namely there is=Mn/Zn,such that=BdasBn/Zn=Bd.However,the replica symmetryZndoes not act smoothly in the bulk,and there are singular points in,the fixed points ofZn.Actually the singular locus inis a co-dimensional two surfaceEn.This co-dim 2 surface can be taken as a cosmic brane with a tension

such that it backreacts onMand deforms it to.As the cosmic brane induces a defect angle 2π/n,the quotient spacehas a conical singularity with the defect angle.

Near the cosmic brane the spacetime metric can be approximated as follows.Let the coordinatesyi,i=1,...,d −1 be the worldvolume coordinates of the brane,and (tE,x) be the transverse normal directions.Here we are working in the Euclidean gravity withtEbeing the Euclidean time.Then the metric is

Introduce the polar coordinates in the transverse direction

To respect the replicaZnsymmetry,as we approachEnwe haveτ∼τ+2πn.Consequently the metric nearEnin the

The first two terms on the right-hand-side show that it is a conical space.From this metric ansatz,the local equation of motion leads to the vanishing condition of the extrinsic curvature of the co-dimension two surfaceKa==0.In other words,the cosmic brane must be extremal surface.In theν→1 limit,the cosmic brane becomes the RT surface

Furthermore,we can compute the on-shell regularized gravity action.Firstly the action of the bulk configurationMnis related to the one ofbyI(Mn)=nI().Thus we have

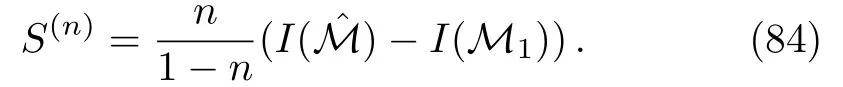
Note thatI()does no include any contribution from the cosmic brane.Next,we have to do analytic continuation and assumento be real,then we find

The on-shell regularized bulk action gets nonvanishing contribution from the boundary terms.More precisely[53]

where the integral is over a co-dimension one tube around the cosmic brane,xα,γαβ,α,β=0,...,d −1 are the coordinates and the induced metric on the tube,andis the normal vector of the tube withµ,ν=0,...,d.Take the metric ansatz above into the formula,we find that

Actually this gives a formula for the holographic Rényi entropy,or the modular entropy.[53]In then →1 limit,we recover the RT formula.

5 Rényi Entropy and Semiclassical AdS3 Gravity

The holographic entanglement entropy is at the intersection of quantum gravity,quantum information and quantum field theory.Its study sheds light on various issues in these areas.We will review three topics: the semiclassical gravity,geometry from entanglement and gravity from entanglement.In this section,we consider the first topic and leave other two topics to the next section.

Even though the AdS3gravity has no local dynamical degrees of freedom,it indeed has global or boundary degrees of freedom.Actually Brown and Henneaux[54]showed that under appropriate boundary conditions the asymptotic symmetry group(ASG)of AdS3Einstein gravity is generated by two copies of Virasoro algebra with central charges

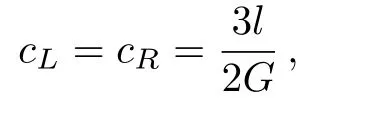
wherelis the radius of AdS3spacetime andis the coupling constant.In modern understanding,this actually suggests that the AdS3quantum gravity is dual to a two-dimensional(2D)CFT with the above central charge,a prototype of AdS/CFT.

There are a few remarkable features in the AdS3/CFT2correspondence.First of all,its setup has nothing to do with the string theory.Therefore it opens a new angle to study the holographic principle.Secondly,the AdS3gravity is solvable in the sense that all of the classical solutions are locally AdS3and are the quotients of global AdS3,such that the path-integral is feasible in principle.[55−56]Moreover,the AdS3gravity could be equivalent to a Chern-Simons theory,which is of topological nature.[57−58]Finally,the 2D conformal symmetry group is infinitely dimensional so that there are powerful analytic tools to study 2D CFTs.Thus,even though the explicit construction of dual 2D CFT is not known,we can still learn many things from universal features of CFT.However,it is remarkable that the precise definition of AdS3quantum gravity is unknown.In Ref.[56],it was shown that the sum of partition function of classical solutions of AdS3gravity is not sensible,raising the issue if pure AdS3gravity is UV complete.Here we focus on the semiclassical regime.

The semiclassical limit of AdS3gravity corresponds to the large central charge limit of holographic CFT.In the context of the semiclassical AdS3/CFT2correspondence,the entanglement entropy has been well understood.In 2D CFT,due to its infinite dimensional conformal symmetries,the direct field computation is feasible.One could insert the twist operators to impose the nontrivial boundary conditions in applying the replica trick.[13,15]As a result,the partition function on a higher-genus Riemann surface could be recast into the correlators of twist fields on a complex plane in an orbifold CFT,which arises from theZnreplica symmetry.For a 2D CFT on complex plane the Rényi entropy for one interval with lengthℓis universal and only depends on the central charge[13]

withϵbeing the UV cutoff.For the entanglement entropyS1,it has been reproduced by the holographic computation in Refs.[1–2].For the generalSn,n >1,they have been reproduced successfully in Ref.[59]from the Euclidean action of corresponding gravitational configurations.For the multi-interval case,the entanglement entropy has been studied from both the field theory[60]and gravity points of view.[59]Moreover,the Rényi entropy for the double interval case has been discussed in Refs.[37,61].For the single interval on a torus case,it has been studied in Refs.[62–64].

The holographic entanglement entropy inspires us to study the Euclidean gravity in more details,beyond classical order.In Subsec.4.3,we have shown that the holographic(Rényi)entanglement entropy is actually captured by the on-shell regularized action of the gravitational configuration.For the semiclassical AdS/CFT correspondence,this suggests that HEE is dual to the leading order entanglement entropy in the largeN(orc) limit.The next-to-leading one in the field theory should correspond to the 1-loop correction of the on-shell action,which could be computed by the 1-loop determinant of the massless fluctuations around the gravitational configuration.[62,65]It was also argued that the 1-loop correction could be from the bulk entanglement of the entanglement wedge.[65]In the semi-classical AdS3/CFT2correspondence,the 1-loop corrections are in good match with the CFT study as well.

5.1 Holographic Rényi Entropy

Let us sketch the essential points in the study of HRE in the Euclidean AdS3gravity.[59]As we discussed before,then-th Rényi entropy is captured by the partition function on a higher genus Riemann surface Σnvia the replica trick.From the AdS/CFT correspondence,we need to find the bulk gravitational configurationMγwhose boundary is the resulted Riemann surface∂Mγ=Σn.Then the regularized on-shell action of the configurationMγshould give the partition function in the semi-classical limit.Note that in this case,the bulk configuration is not a minimal surface.The key point is that all the classical solutions of AdS3gravity could be obtained byMγ=H3/Γγ,whereH3is the Euclideanized AdS3,i.e.hyperbolic space or Poincare half space,and Γγis the subgroup of the isometrySL(2,C) ofH3.If we focus on the handlebody solutions,as we will,the subgroup turns out to be the Schottky group.On the boundary,the Schottky group Γγacts onCby the linear Mobius transformation such thatC/Γγ=Σn.The basic strategy to compute the holographic Rényi entropy(HRE) is as follows:

(i) For a fixed Riemann surface,find its Schottky uniformization.

(ii) Extend the Schottky uniformization to the bulk to find the gravitational solution.

(iii) Compute the classical regularized bulk action to read the HRE.

Every compact Riemann surface could be obtained by the Schottky uniformization.The uniformization map is determined by a second order differential equation of Fusian type

There are two independent solutions,and their ratiow=ψ1/ψ2gives the quotient map.More importantly,Tzzis the stress tensor of a Liouville-type CFT.Its explicit form depends on (3g −3) complex accessory parameters with respect to the holomorphic quadratic differentials on the Riemann surface.After imposing the monodromy conditions on the cycles of the Riemann surface fix the accessory parameters and then allows us to solve this ordinary differential equation.However,in practice this is usually a hard problem.

The other essential point is that the on-shell regularized bulk action of gravitational configurations in pure AdS3gravity is captured by a Liouville type action on the boundary.[66]More importantly the dependence of this so-called Zograf-Takhtadzhyan action[67]on the accessory parameters is determined by a differential equation

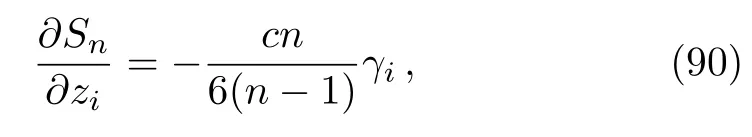
whereγiare the accessory parameters,being fixed by the monodromy problem.For a general Riemann surface of high genus,it is a difficult problem to determine this regularized action,even perturbatively.Nevertheless,for the Riemann surface in computing the Rényi entropy,the problem is simplified due to the replica symmetry.There are two workable examples: the double intervals on a complex plane with one cross ratio and the single interval on a torus.

There is another subtle issue.For the same Riemann surface Σn,there could be more than one Schottky uniformization and correspondingly more than one gravitational configurationsMγwith different actions.From the path-integral of Euclidean gravity,we should pick the configuration with the least action.

Let us first consider the HRE in the double interval case.Now the stress tensor is of the form

where

Due to the replica trick,there is only one conformal invariant accessory parameter.The accessory parameters are determined by requiring trivial monodromy at the infinity and on either theA-cycle orB-cycle,withA-cycle enclosing the near branch points of different intervals and theB-cycle enclosing one of the intervals.This case has been discussed carefully in Ref.[59].

For the single interval on the torus,the stress tensor is[62]

where℘is the doubly periodic Weierstrass function,and

On the torusz∼z+mL+inβ,there are a thermal cycle and a spacial cycle.We can set trivial monodromy along one of these two cycles and the cycle enclosing two branch points,so that the identification of the other cycle gives the generator of Schottky group.At a high temperature above the Hawking-Page transition,the bulk spacetime is actually a black hole,so the time direction is of trivial monodromy,while at a low temperature,the bulk dual is the thermal AdS spacetime,so the spacial direction is of trivial monodromy.There actually exists a duality between high temperature and low temperature phase

In fact,for the single interval on the torus,the relation(90)is not enough to determine the HRE completely.This is because that the torus itself has shape,which affect the action.For the torus at high temperature,we have to consider the effect of its finite size.In other words,the regularized action depends not only on the accessory parameter,but also on the size of the torus[63]

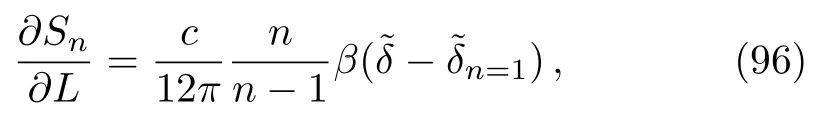
The above treatment is universal,even for the AdS3vacuum in other 3D gravity theory.[68]Simply speaking,the holographic Renyi entropy(HRE)is given by the classical regularized action of the corresponding gravitational configurations.In fact,with the Schottky uniformization,one can study the HRE beyond classical gravity regime as well.

The 1-loop correction to the HRE can be computed in the following way.The gravitational configurations for HRE are generated by the Schottky group.Now we have to consider all the fluctuations around the configuration,and compute their functional determinants,which gives the 1-looop correction.These 1-loop determinants have been discussed before[69−70]by using the heat kernel and method of images onH3/Γ.The 1-loop partition function reads

Here the product oversis with respect to the spins of massless fluctuations andPis a set of representatives of primitive conjugacy classes of the Schottky group Γ.qγis defined by writing the two eigenvalues ofγ ∈Γ asq±1/2γwith|qγ| <1.It is obvious that the contributions of the fields with different spins could be separated.From the above formula,one has to find the Schottky group Γ corresponding to Σnand generate the primitive conjugate class,which is defined asP={non-repeated words up to conjugation},e.g.

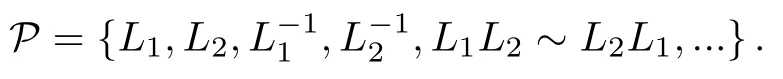
Then one can compute the 1-loop correction by working out the eigenvalues of all primitive elements and summing them up.Usually the number of the primitive elements is infinite.Fortunately for the two examples we are interested in,only finite number of them contribute to the expected order of expansion.[62]For double intervals with small cross ratiox,only finitely many words contribute to each order inx.For single interval on a circle at finite temperature,similar strategy works in the low temperature and high temperature limits.

5.2 CFT Study

From the AdS3/CFT2correspondence,it would be interesting to compute the Rényi entropy directly in the large central charge limit.The explicit construction of the CFT dual to the AdS3gravity is not clear,but it is expected to have a sparse light spectrum[60,71]As discussed before,for the multi-interval case,the Rényi entropy is encoded in the correlation function of the twist operators.This multi-point correlation function could be expanded by the conformal block.In the large central charge limit,the dominant contribution comes from the vacuum module.[60]The vacuum module consists of the identity operator and its descendants made of the stress tensor.In AdS3/CFT2,the stress tensor in CFT is dual to the massless graviton in the bulk.If one considers the other fluctuations,say higher spin fields,in the bulk,then one has to take into account of the contribution from the other primaries.From the computation,we can not only read the leading order contribution,linear toc,corresponding to the classical HRE,but also get the next-to-leading order contribution,independent ofc,corresponding to the 1-loop quantum correction to HRE.We find remarkable agreements on both sides.

For the double interval case,we would like to consider two short disjoint intervals on the complex plane.[37]Without losing generality,we chooseA=[0,ℓ]∪[1,1+ℓ]withℓbeing small,and thus have a small cross ratiox=ℓ2.The resulting Riemann surface for then-th Rényi entropy is of genusn −1 such that the partition function on it is hard to compute.Nevertheless,when the intervals are short,we can consider the operator product expansion(OPE)of two twist operators,which are near each other:[12,36−37]

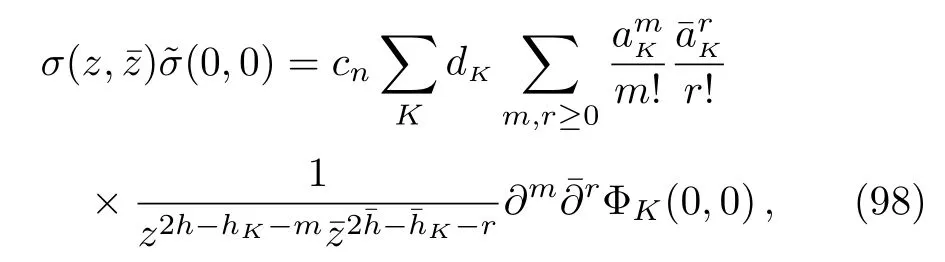
with the summationKbeing over all the independent quasiprimary operators of CFTn.To use the OPE of the twist operators,we have to find the quasiprimary operators level by level.As the holomorphic and antiholomorphic sector are decoupled and similar,we may just focus on the ones in the holomorphic sector.The detailed discussion can be found in our works.[37,61]The process in straightforward but tedious.

We are interested in the Rényi mutual information(RMI)

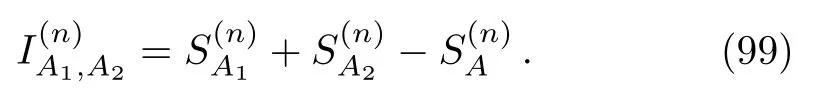
In the following,we writeInfor.The RMI is

Here we have classified the contributions according to the order of 1/c.We found that the leading order result,∗∗The leading order contribution can be also computed from the conformal block,which could be read recursively.[60,72]which is linear inc,are in perfect match with the bulk computation[12,59−60]up to orderx8,and the next-toleading order result are in exact match with the bulk 1-loop result[12,62]up to orderx8.More importantly,we found that the nonvanishing next-next-to-leading order result,which suggests that the 2-loop quantum correction to the handle-body configuration is generically nonvanishing.[69]This issue has been further addressed in Ref.[73].

For the single-interval on a torus,let us first consider the case that the temperature is low and the interval is short.We set the circle length to beL,the interval length to bel,and the temperature to beT=1/β.At a finite temperature,the density matrix becomes thermal

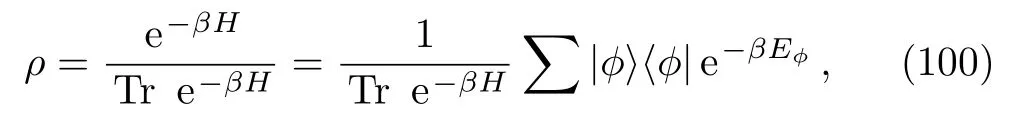
where the summation is over all the excitations in the theory.On a cylinder the energy spectrum is read by

Thus we can expand the thermal density matrix according to the level.The essential point is that expanding the thermal density matrix is equivalent to insert a complete set of state bases along the thermal cycle such that the torus becomes a cylinder.By a uniformization conformal map and the state-operator correspondence,the computation is recast into the sum of multi-point functions on then-sheeted cylinder.[74]It turns out that both the classical and 1-loop part of the Rényi entropy are in perfect agreement with the holographic computation,up to orderO(e−8π/TL).[63]

In the large interval limit,the above computation breaks down.This could be easily seen in the holographic picture.At high temperature,the dual spacetime is a BTZ black hole.It seems that the holographic entanglement entropy should be computed by the geodesic length in the black hole background

However,it turns out not to be the complete story.It has been found[75]that when the intervalλ →L,there exists another possibility: the geodesic may break into two pieces,one encircling the horizon of black hole,and the other ending on the complementary interval.Moreover,the length of the disconnected curve is shorter and gives the holographic entanglement entropy:[44,75]

It is more illuminating to change the above relation into a field theory relation between the thermal entropy and the entanglement entropy

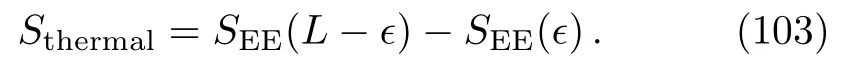
The relation is reminiscent of the saturated Araki-Lieb inequality[27]

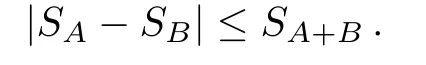
It was conjectured that the relation (106) should be true for any CFT,not only for the CFT with a holographic dual,and at any temperature.This relation has been proved for a general CFT with a discrete spectrum,by deforming the branch cut in an appropriate way.[76]

In the large interval limit,the entanglement entropy becomes singular.One has to find a new way to compute them.We proposed[77]that we should insert a complete state bases at the cycle crossing the branch cut.As the fields have non-trivial monodromy when they move from one sheet to the next one,we had to consider the twist sector of the orbifold CFT carefully.We studied the twist sector state carefully and tested our proposal in the case of free boson,after correcting some errors in the literature.[77−78]We also used this expansion to prove the above universal relation between the entanglement entropy and thermal entropy.

Using the above proposal,we studied the large interval Rényi entropy for the holographic CFT.[64]On the CFT side,we may focus on the twist sector of the vacuum module.The computation could be transformed into the correlators on a complex plane with multiple cuts at different positions.The leading order contribution comes from the so-called twist vacuum module,which was generated by the Virasoro generators on the twist vacuum.The computation is related by the Ward identity to the correlation function of four twist operators,two on the branch points and the other two at the left and right infinity.For the next-leading contribution,one has to consider the excitations in the twisted sector.

It is more difficult to study the holographic Rényi entropy in the large interval limit.From the holographic study,[75]it indicated that the gravitational configuration should be very different from the short interval case.In other words,we have to find a different set of monodromy condition to read the Schottky uniformization.We set the trivial monodromy condition on the following cycles

(i) The cycle which goes across the branch cut forntimes.

(ii) The othern −1 independent cycles enclosing the complementary interval.

With these monodromy condition,we solved the ordinary differential equation for the uniformization map and read the classical HRE and its 1-loop quantum corrections.We find that both the classical and 1-loop contributions are in good agreements with CFT results.

Besides the above two examples,we have shown that the 1-loop determinant of the handlebody solutions (97)can be reproduced from the field theory.The basic idea is that in the largeclimit,the vacuum sector of the CFT becomes essentially free.Then the orderO(c0) partition function is determined by the multi-point functions in the Riemann sphere via sewing prescription.This allows us to recover (97) by using combinatory method.[79]

The above discussions focus on the AdS3gravity with Brown-Henneaux boundary conditions.As the threedimensional quantum gravity is defined with respect to the asymptotic boundary condition,holographic entanglement entropy under other sets of consistent boundary conditions have been investigated.For example,the HEE in the AdS3gravity under Comp`ere-Song-Strominger (CSS)boundary conditions[80]has been studied in Refs.[81–82].The entanglement entropies in the WAdS/CFT[83]and flat holography[84−85]have been discussed as well.The Rényi mutual information of two disjoint interval in holographic warped CFT has been studied recently in Ref.[86].

6 Geometry,Gravity and Entanglement

6.1 Geometry from Entanglement

The most interesting implication of HEE is on geometry from entanglement.The appearance of minimal surface in the bulk suggests that the geometry could be from the entanglement at the boundary.Such a picture is in accord with J.Wheeler’s slogan “It is from Qubit”.This inspired people to investigate how the holographic map between quantum field theory and gravitational dynamics actually works from the point of view of entanglement entropy.

One interesting observation is on the analog between tensor network and RT surface,first found by Swingle.[87]In the AdS/CFT correspondence,there is a UV/IR relation,which states that the radial direction in the AdS space could be taken as the energy scale of the field theory such that the infrared cutoff at the asymptotical AdS boundary corresponds to the ultraviolet cutoff in the field theory.Therefore probing deeper into the bulk corresponds to probing the quantum state in lower energy scale.This behavior could be related to the tensor network constructions for the ground state of interacting many-body lattice systems by performing the coarse graining transformations.Qualitatively the entanglement of a segment in tensor networks could be related to the RT surface.This fact motivated people to study the AdS holography from tensor networks.[88−90]

One essential question in the AdS/CFT correspondence is to understand under what circumstances a field theory state could be dual to a smooth semiclassical geometry.Not every state in field theory can be dual a semiclassical geometry,for example,in AdS5/SYM4most of states could be dual to highly stringy states,which have no geometrical description.It was suggested that the entanglement could be a diagnostic for the emergence of the geometry.[91−92]A typical example is the thermofield double state

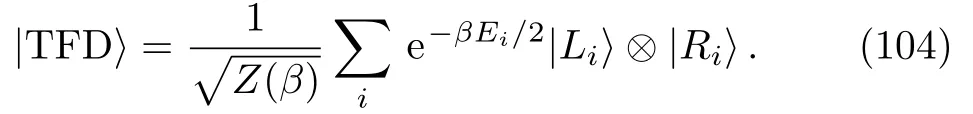
Here one considers two copies of the QFT,one being labelled byLand the one byR,are the states of energyEi.The TFD state is an entangling state of energy eigenstates,weighted by a Boltzmann factor.After tracing out the degrees of freedom inL,one gets the reduced density matrix

suggesting the state is in a thermal mixed state.At low temperature,β ≫1,the ground state dominates and the entanglement entropy ofRis almost vanishing.On the other hand,at high temperatureβ ≪1,the state is highly entangled with an entropy being of orderO(1).From the AdS/CFT correspondence,the low temperature phase corresponds to a thermal AdS,while the high temperature phase corresponds to a Schwartzschild-AdS black hole.More precisely the low temperature TFD state is holographically described by two copies of AdS spacetime,which are disconnected,while the high-temperature TFD state is described by the Lorentzian Sch-AdS solution with two asymptotic regions,which are connected by a spatial Einstein-Rosen (ER) bridge.In other words,the TFD state with a macroscopic entanglement is characterized by a geometric dual where two entangled parties are spatially connected.This connection between geometry and entanglement was prompted by Maldacena and Susskind[93]to argue for a more general relation,“ER=EPR”.

More generically,the criteria for geometric duals to field theory states are under intense investigation.Some of them rely on the entanglement entropy.The entanglement entropies in field theory should satisfy various entropy inequalities,which should be respected by the geometric duals.It was shown in Ref.[94]that the gravitational configurations supported by matter violating the null energy condition(NEC)would lead to the breakdown of the strong subadditivity inequalities.This is in accord with the theorem by Gao and Wald,[95]which suggests that if the matter satisfying the null energy condition the bulk causal structure is compatible with the boundary causal structure.

The above question that which field state can have a geometric dual can be changed into another important question: what is the bulk dual of a density matrix?This question is closely related to the bulk reconstruction,which is to understand the bulk locality of a classical gravitational theory from dual CFT.††One way is to reconstruct the local bulk field from boundary data.Since the earlier days of AdS/CFT,this question has been studied by many researchers.There are lots of study on this issue.For a nice review on the bulk reconstruction,see Ref.[96].It turns out[97−98]that the region of the bulk spacetime dual to the density matrix is the so-called entanglement wedge.The entanglement wedge is constructed as follows.Given a subregionAat the boundary,one may define the reduced density matrixρAwith respect to the CFT vacuum.The holographic entanglement entropy is determined by the extremal surfaceEA,which is homologous toA.In the bulk,one gets a codimension-1 homology surfaceRA,which is bounded byEAandA.Then the entanglement wedgeWE(A) is defined to be the bulk domain of dependence of the homology surface

Note that the bulk spacetime can be decomposed into

which is similar to the decomposition of the boundary spacetime into four regions with respect to the subregionA

In the semiclassical picture,the 1-loop correction to the entanglement entropy is actually given by the bulk entanglement across the extremal surfaceEA,i.e.

AsWE(A) is a domain of dependence,Sbulk(RA) can be computed on any spacelike surface foliating the entanglement wedge.The pieces of evidence supporting the above picture come from the semi-classical AdS/CFT correspondence and viewing the holographic map as a quantum error-correcting code.[99−101]

6.2 Gravity and Entanglement

In the above,we have introduced how the geometry can be reconstructed from the entanglement in the boundary CFT.One closely related question is how the gravitational dynamics emerges from the entanglement point of view.In Refs.[102–103],it has been shown that the linearized Einstein equation could be derived from the first law of entanglement entropy.Such kind of study has been pushed to the non-linear level,up to cubic interactions.[104]In the following,we outline the idea underlying this study.

The first law of entanglement entropy states that the first order variation of entanglement entropy is equals to the first order variation of the expectation value of the modular Hamiltonian

In general,the modular Hamiltonian is nonlocal and very complicated.However,if we consider a ball-shaped spatial region of radiusRcentered atx0,denotedB(R,x0)then its modular Hamiltonian in a vacuum state of a CFT takes a simple form

whereTttis the energy density.Thus,given a perturbation to the vacuum,we have

The vacuum entanglement entropy of a ball-shaped region in flat spacetime can be interpreted as the thermal entropy of the CFT on a hyperbolic cylinder.[48]Let us start from the flat space in a polar coordinates

and consider the coordinate transformation

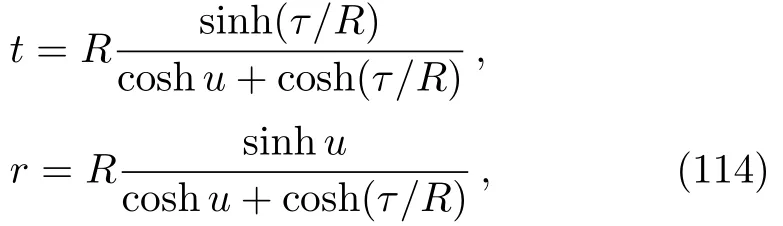
then we find the metric

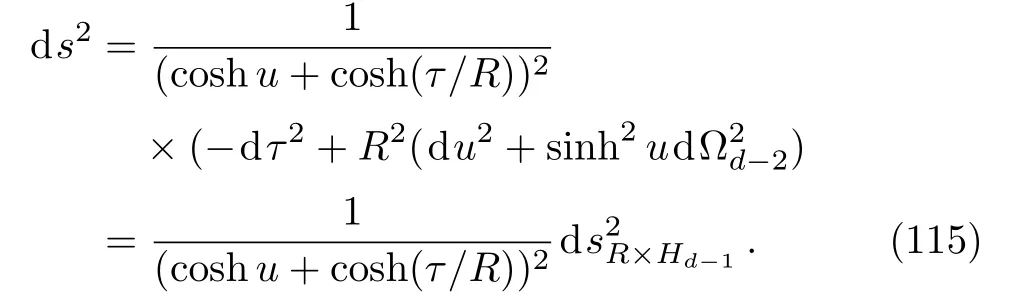
Namely the flat spacetime is conformally related to the hyperbolic cylinder.After rewriting the metric of hyperbolic space in terms of Poincarcoordinates,the hyperbolic cylinder could be conformally related to the Rindler geometry.The modular Hamiltonian for the Rindler space is just the Minkowski boost generator[105−106]

which allows us to get Eq.(111).Moreover,as a Rindler observer sees the Minkowski vacuum as a thermal state,the reduced density matrix for the Rindler wedge is simply a thermal density matrix with a temperature 1/(2πR).As a result,the reduced density matrix of the hyperbolic space must also be a thermal density matrix

where the temperature is related to the radius of the hyperbolic space

Therefore the entanglement entropy ofB(R,x0)is related to the thermal entropy at temperature 1/(2πR).

On the other hand,the hyperbolic cylinder at a temperature is holographically dual to a Rindler slicing of AdSd+1,which is a black hole spacetime with metric

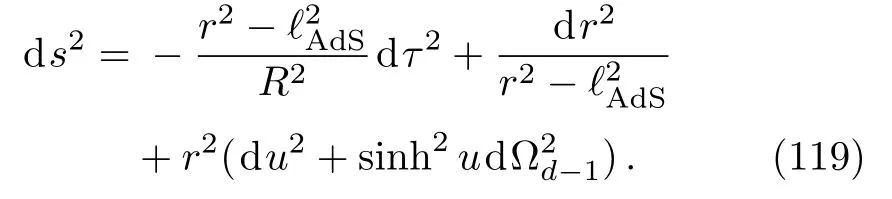
The entanglement entropy is simply given by the black hole entropy,and the modular Hamiltonian is now related to the time translation in the background and is given by the energy of the black hole measured at infinity.

Now consider a small perturbation to the vacuum state,the first law (112) is expected to be held.This law could be changed into the first law of the black hole dynamics which in turn requires that the bulk satisfies the linearized Einstein equation.The details can be found in Refs.[102–103].The study can be generalized to the holographic CFT dual to the higher curvature gravity.

The positivity and monotonicity of the relative entropy have interesting constraints on the gravity.Consider the relative entropy between the vacuum state and another excited state.For the states that are infinitesimally apart,the positivity of the relative entropy would imply the linearized Einstein equation,as we show above.Moreover,the positivity of the quantum Fisher information implies that the perturbative expansion of the canonical energy to quadratic order is non-negative definite,and more generally the positivity of the relative entropy implies a positive energy theorem.[107−108]

7 Ending Remarks

In the past decade,the holographic entanglement entropy has brought the researchers working on quantum information,quantum field and quantum gravity together,and inspired new research directions.In this brief review,we only touched the tip of an iceberg.There are lots of unanswered questions in the field.The best thing will come in the future.

Acknowledgments

Bin Chen would like to thank the participants of the Fall School on Holography and its Application(Nov.8–18,YangZhou) for various questions,and the participants of the advanced workshop “Dark Energy and Fundamental Theory” for stimulating discussion.