Scalar Tensor Cosmology With Kinetic,Gauss-Bonnet and Nonminimal Derivative Couplings and Supersymmetric Loop Corrected Potential
Rami Ahmad El-Nabulsi
Athens Institute for Education and Research,Mathematics and Physics Divisions,8 Valaoritou Street,Kolonaki 10671 Athens,Greece
Abstract We discuss a particular four-dimensional cosmology based on non-minimal scalar tensor theories characterized by a supersymmetric loop corrected potential and a Hubble parameter defined as a function of the scalar field.Power-law solutions are obtained in the FRW background giving rise to acceleratedly expanding universe characterized by a scale factor and a scalar field depending both on the non-minimal coupling parameter ξ.Based on SNeIa data and on Hubble data X-ray gas mass fraction measurements,we find 0.116<ξ <0.225 which results on a universe dominated by vacuum energy.
Key words: scalar tensor cosmology,Gauss-Bonnet coupling,non-minimal derivative coupling,vacuum energy
The nature of both dark energy and dark matter represents an open and serious problem in cosmology and high energy physics.Recent astrophysical observations prove that dark energy fills 70% of the universe whereas dark matter fills around 25%.[1]Different phenomenological approaches were presented in the last years to attribute realistic physical candidates for both energies.Some wellknown dark matter candidates are the weakly interacting massive particles beside exotic particles proposed within phenomenological theories beyond the standard model of particle physics.[2−3]As for dark energy,the problem is tricky yet a large number of theoretical models were proposed in literature to explain its proper nature and which are confronted with observations.The simplest model of the dark energy is the cosmological constant with equation of statew=−p/ρ=−1 (assuming the universe is filled with barotropic fluid with energy densityρand pressurep).Although there are still a number of theoretical problems,the cosmological constant models are consistent with the current observations.[4]Besides some of these models include the attribution of dark energy to some kind of exotic matter like quintom fields[5]or by modifying the Einstein’s theory of general relativity (modified gravity theories) which are somewhat motivating.[6−7]Some of these modified gravity theories are characterized by the presence of scalar fields,which are of particular interest for cosmologists and theoretical physicists for several analytical and fundamental reasons.In fact,the presence of scalar fields in the field equations simplifies considerably the mathematical analysis of the cosmological model under study.Moreover,scalar fields are connected to the idea of varying fundamental constants in nature initiated by the Brans-Dicke model.[8−9]Additional motivations are related to higher-order dimensional theories like the Kaluza-Klein and superstring theories,which are believed to be the most promising candidates to quantum gravity.Besides,scalar fields play a crucial role in inflationary scenarios and the physics of the early universe in addition to their role in explaining the nature of dark energy.[10−11]These scalar theories are appealing since they could be confronted with observations and accordingly it is possible to select the cosmological theory,which fits the most observational data.There exist plenty of arguments that make us believe that both modified gravity and scalar theories required more studies.It is noteworthy that numerous theoretical competitive models trying to explain the physical nature of the dark energy component have been proposed in literature,e.g.Chaplygin gas,Generalized Chaplygin gas model,Kessence,holographic theory and so on (see Ref.[12]and references therein).Despite their appealing properties,no consistent convincing cosmological theory,which may explain the universe from its singularity at the origin of time till its late-time accelerated expansion exists.Nevertheless,non-minimal derivative coupling theories between the scalar field and the curvature are of particular interest since they play important roles at different energy limits of the universe where scalar fields display a leading role in acceleratedly expanding cosmological models.In the present letter,we discuss a particular non-minimal derivative coupling model described by the action (in natural units=c=1):
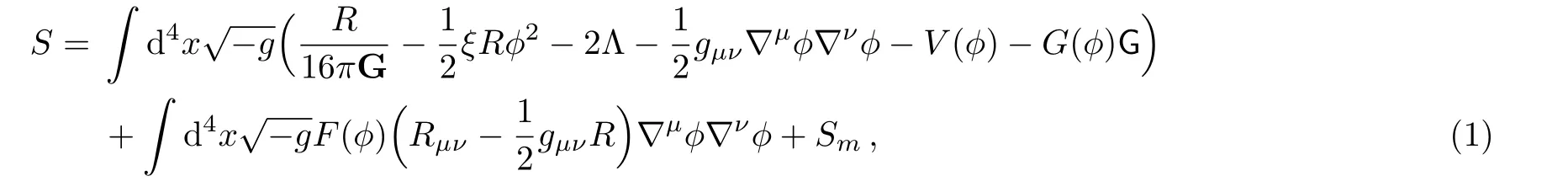
where∇µis the covariant derivative,Ris the scalar curvature,ξis a non-minimal coupling parameter,ϕis the scalar field,G=R2−4RµνRµν+RµνρσRµνρσis the 4-dimenional Gauss-Bonnet invariant,F(ϕ) (of dimension square of the length) andG(ϕ) (dimensionless) are coupling functions of the scalar field,gis the metric,Λ is the cosmological constant,G is the gravitational coupling constant,Smis the action of matter,V(ϕ) is the scalar field potential,andω(ϕ) is the kinetic term.This action generalizes the model described in Refs.[13–15].The presence of the potentialV(ϕ) plays an important role in cosmology and is considered as a very vital element of various cosmological models.[16]In spite of the fact that this action may not be derived from string theory,it may be significant on its own right to explore its cosmological implications.It is notable that the coupling between the scalar field and the Gauss-Bonnet invariant was explored largely in literature since it plays an important role in the study of dark energy and quintessence in the physics of the late-time universe.[17−20]It is inclusion in the theory is motivating since it affects the late-time cosmological dynamics by adding the 2nd-order derivative terms to the Friedmann equations of motion.Moreover,the role of the non-minimal coupling of the typeξRϕ2in late-time cosmology has been explored in different works.[21−26]Several motivating features were revealed as superacceleration,tracker solutions,and phantom behavior in addition to its confrontations with observations (see Ref.[27]and references therein).In this study,we consider a general scalar field model that contains the non-minimal couplingξRϕ2,the Gauss-Bonnet invariant,the non-minimal derivative coupling to the Einstein’s tensor in addition to the cosmological constant and the scalar field potential.Our main aim is to study this model and its implications in the late time dynamics of the universe and the role of these coupling at cosmological scales.The field equations followed from the action (1) after varying the action with respect togµνandϕare respectively:

Tµν=(p+ρ)uµuν+pgµνis the standard-model matter energy-momentum tensor which is conserved and⊔⊓is the covariant D’Alembert operator.Throughout this work we consider a spatially flat,homogeneous and isotropic background with metric:
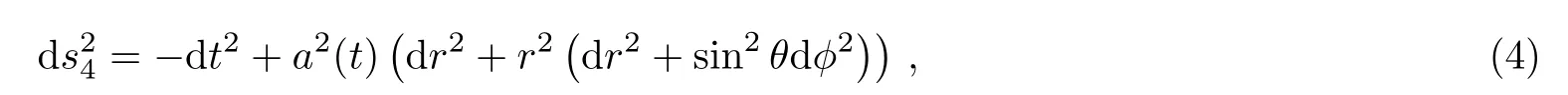
wherea(t) is the scale factor.θandϕare the two angular coordinates.The field equations (2) and (3) give rise to the following system of coupled differential equations:
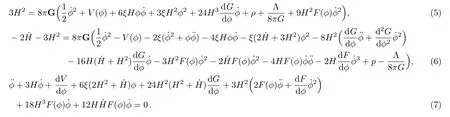
In what follows we study cosmological implications of Eqs.(5)–(6) and look for plausible solutions giving rise to accelerated expansion of the universe.However,in place of imposing a power-law expansion solution of the scale factora(t)∝tpwithpbeing a real parameter as done in Ref.[15],we suppose that the Hubble parameter could be defined as a function of the scalar field asH=H(ϕ)=hϕm,h,andmare real parameters.Such dependence was explored in literature through different arguments[28−38]and it has many interesting advantage since the entire parameters of the cosmological model under study could be derived accordingly.Besides,such the relationH(ϕ)=hϕmsimplifies considerably the nonlinear differential equation (7).In this study,we consider power-law couplingsF(ϕ)=αϕx,G(ϕ)=βϕy,and additionally a potential of the formV(ϕ)=γϕz+χlnϕwhere(α,β,γ,χ)and(x,y,z)are real parameters.Such a type of potential with a logarithmic correction appears in supersymmetry,supergravity,and M/string theory.[39]In fact,most theorists consider renormalizable tree-level quadratic and quartic convex potentials with vanishing minimum to deal with inflation and accelerated expansion of the universe.However,it was observed that many supersymmetric (SUSY) cosmological models (loop corrected potentials)characterized by a logarithmic non-convex potential of the formV(ϕ)=A+χlnϕholds a number of remarkable features (in particular forA >0) and may be adequate to explore both the high energy and the low energy limits.[40−43]Logarithmic potentials also have proved to successfully drive slow-roll inflation of the universe.[44−45]Besides,logarithmic dark energy potentials were explored more recently in Ref.[46]and offer new features in dynamical quintessence cosmology.For these reasons,we adopt in this study a power-law potential with an SUSY logarithmic correction.Equation (7) is therefore reduced after some algebra to:
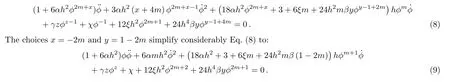
In particular form=−1,z=−1,γ=72h4β,6αh2=−1,(α <0) andχ=−12ξh2,Eq.(9) is reduced to the 1storder differential equation (for non-constant scalar fieldϕ):
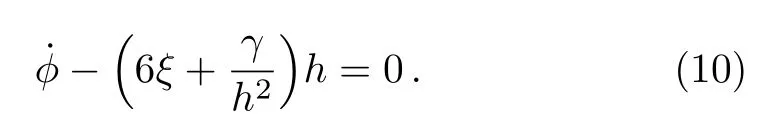
One naturally asks about the real motivation for the previous special choices of parameters since a large number of choices may arise and for every choice,one has a kind of evolution of “our universe”.In fact,Eq.(8)is a 2nd-order nonlinear differential equation whose solution is constrained by the parameters introduced in the theory.However,our main aim is to obtain power-law cosmology,which is often used in several astrophysical observations since one needs only one parameter to adjust the rate of expansion.Besides,power-law model is a good phenomenological description of different asymptotic regimes of cosmic evolution at different epochs of time ranging from radiation to dark energy epoch.[47]Besides,it was found more recently that,in the frame of non-minimal and Gauss-Bonnet couplings,the power-law solution passes several tests including the gravitational waves speed test and remains consistent even after GRB 170817A.[48]It is noteworthy that in simple inflationary model,the power-law can eliminate flatness and horizon problems with simple spectrum.[47,49]In view of all these outcomes,one possible way to obtain within the present non-minimal couplings model a viable power-law cosmology is to linearize the nonlinear differential equation (8).This was done by selecting the previous particular parameters.Assuming the initial conditionϕ(0)=0,the solution is given by:
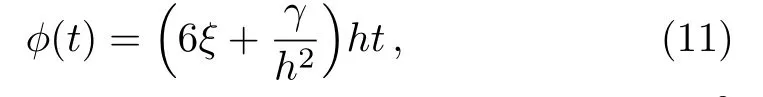
and consequently the scale factor varies asa(t)∝t6ξ+γh−2whereas the coupling functions take the following formsF(ϕ)=αϕ2=−(1/6)h−2ϕ2andG(ϕ)=βϕ3=(γ/72)h−4ϕ3.Forγ=h2,we finda(t)∝t(6ξ+1)andH(t)=(6ξ+1)/t.The SUSY potential in our approach takes therefore the logarithmic form:
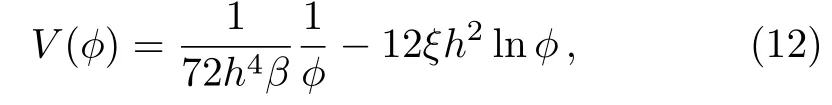
which corresponds to an inverse power-law potential with a logarithmic correction.It is noteworthy that the inverse power-law potential is one of the prototype quintessence potentials that hold several desired properties.[50]In addition,inverse quintessence potentials are used in cosmological scenarios unifying dark energy and dark matter[51]besides to study cosmological models with tachyon fields.[52]We observe that forξ=1/6 which corresponds for a conformal coupling scenario,the scale factor evolves asa(t)∝t2which corresponds for an acceleratedly expanding universe.In fact,the case of conformal coupling has many promising features in low energy scales cosmology(see Refs.[53–54]and references therein).The scalar field for this particular case evolves asϕ(t)=2ht.From Eqs.(5) and (6) we get effortlessly:
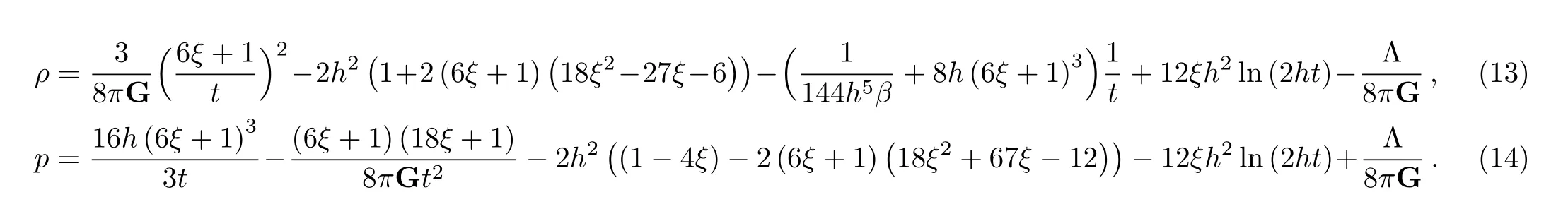
Assuming the equation of state (EoS)p=whereis the EoS parameter,we obtain:
Equation (15) corresponds to a time-dependent EoS parameter.For very large time,Eq.(15) is approximated by=−1,which corresponds to a universe dominated by a cosmological constant and is acceleratedly expanding with time.The deceleration parameter is given byq=−/=−6ξ/(6ξ+1).The numerical constraints obtained from SNeIa data,Hubble data X-ray gas mass fraction measurements giveq=−0.3077and therefore 0.116<ξ <0.225.Besides,astronomical observations give1≡−1.006±0.045.[56]The EoS parameter is therefore within the limits of observations.To summarize,the non-minimal coupling added to the GB coupling allow exact solutions that give rise to an accelerated expansion of the universe dominated by the cosmological constant or vacuum energy at very large time and is consistent with current astrophysical observations.The Lagrangian of the theory takes in our assumptions the following form:

whereLmis the Lagrangian of the matter field and where the potential is given byV(ϕ)=h2(ϕ−1−12ξlnϕ).Since the scalar field increases linearly with time,the potential falls to minus infinity yet the Hubble function tends to zero.This is in contrast to the scenario discussed in Ref.[57],which describes collapsing universes.More recently in Ref.[58]it was observed that in cosmological models with negative potentials,the universe may reach a turning point where its energy density tends to zero and then contracts to a singularity.Some cosmological models with negative potentials lead to an oscillatory cosmic evolution of the universe.[59]General properties of the present model crucially depend on the constraintγ=h2.Forγ=−h2,we finda(t)∝t6ξ−1and hence accelerated expansion of the universe occurs ifξ >0.33,which does not lie within the observational limits.A new motivating feature of the model is that the scalar field increases linearly with time asϕ(t)=(6ξ+1)htand depends on the values of the non-minimal coupling parameterξand the parameterhbased on the scaling lawHϕ=h.The power-laws solutions obtained in this study prove that we have a graceful exit from inflation,which leads to the successful reheating,radiation and matter dominant universe.Besides,the above results show that the SUSY logarithmic potential may be used to describe vacuum dominated accelerated universe.In order to carry out the comparison between the observational and theoretical results,one may introduce the redshift 1+z=a−1where we have assumed thata0≡a(t0)=1,t0being the present age of the universe.However,a relation between the cosmic timetsince the Big Bang in terms of the redshift of light emitted attwas established in Ref.[60]and is given byt=2H0/(1+(1+z)2) whereH0is the Hubble parameter.For an appropriate choice ofH0≈70 km/s/Mpc we findt ≈28/(1+(1+z)2)Gyr.Adopting this law,we obtain:
We plot in Figs.1 and 2 the variations of Eqs.(17)and (18) for 0.116< ξ <0.225 andh=1 for numerical illustration purpose:
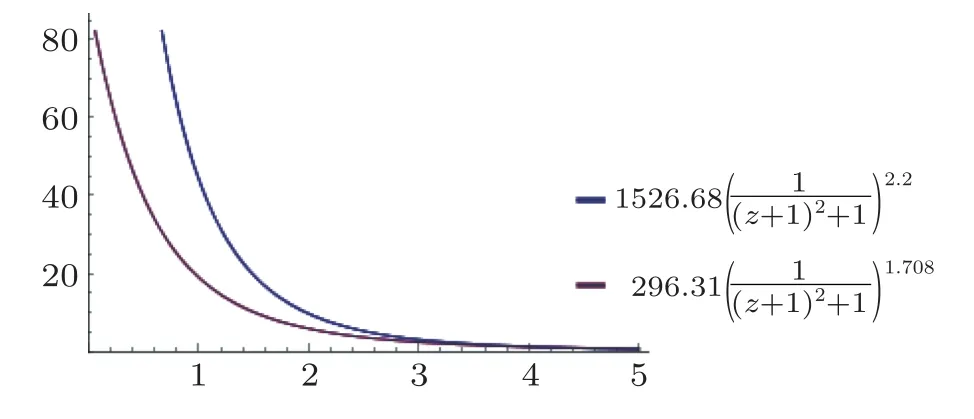
Fig.1 (Color online) Variations of a(z) (vertical axis) with respect to z (horizontal axis) for two different values of ξ:ξ=0.2 (blue curve) and ξ=0.118 (red curve).
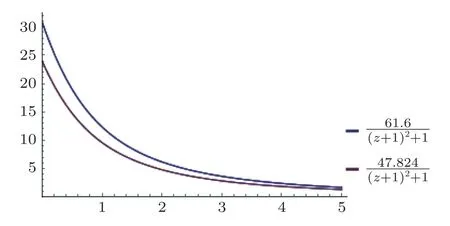
Fig.2 (Color online) Variations of ϕ(z) (vertical axis) with respect to z (horizontal axis) for two different values of ξ:ξ=0.2 (blue curve) and ξ=0.118 (red curve).
The scale factora(z) represented in Fig.1 is a monotonically decreasing function of the redshift or in other words a monotonically increasing of the cosmological time indicating obviously an accelerated expanding universe.In conclusion,non-minimal derivative couplings with kinetic and Gauss-Bonnet couplings characterized by an SUSY logarithmic potential and the inverse lawHϕ=hoffer a new framework to study late-time dynamics of the universe and offer a plausible solution to the dark energy problem.Our model provides power-law solutions,which describes an acceleratedly expansion of the universe constrained by the numerical values of the non-minimal coupling parameterξ.It was observed that the EoS parameter is time-dependent yet for very large time it tends to−1,which corresponds to a vacuum dominated universe.These outcomes prove that the scalar-tensor description of the universe with logarithmic quantum corrections might play a significant role in the explanation of the dark energy and elucidation of the role of the cosmological constant problem or vacuum energy in late-time dynamics of the universe.
Acknowledgments
The author would like to thank the anonymous referee for his useful comments and valuable suggestions.
 Communications in Theoretical Physics2019年7期
Communications in Theoretical Physics2019年7期
- Communications in Theoretical Physics的其它文章
- Tunable Range Interactions and Multi-Roton Excitations for Bosons in a Bose-Fermi Mixture with Optical Lattices∗
- Holographic Entanglement Entropy: A Topical Review∗
- Doubly Excited 1,3Fe States of Two-Electron Atoms under Weakly Coupled Plasma Environment∗
- A Renormalized-Hamiltonian-Flow Approach to Eigenenergies and Eigenfunctions∗
- Constraints on H0 from WMAP and BAO Measurements∗
- Hydrodynamic Stress Tensor in Inhomogeneous Colloidal Suspensions: an Irving-Kirkwood Extension∗
