高拱坝-地基系统整体稳定强震破坏机理研究

涂 劲，廖建新，李德玉，王立涛

（1.中国水利水电科学研究院，北京市 100048；2.中国三峡建设管理有限公司，北京市 100038）

0 引言

2015年9月1日起开始实施的能源行业标准《水电工程水工建筑物抗震设计规范》（NB 35047—2015），总结了国内诸多水电工程水工建筑物抗震设计的实践经验，在大坝抗震设防水准框架、设计地震动参数的确定、大坝及地基岩体动态性能参数的取值以及拱坝动力分析方法、内容和深度等方面均有所变化。新规范对大坝抗震安全分析及评价建议了以坝体和基岩典型部位的变形随地震作用加大而变化的曲线上出现拐点作为大坝地基系统整体安全度的评价指标。然而，超载曲线上拐点的出现与坝体-地基系统变形累积状况的关系如何，是否反映坝体-地基系统的受力工作性态从量变到质变的过程，尚待通过进一步的研究来揭示。

本文对某重大高拱坝工程，在按照新规范采用场地相关的设定地震反应谱及相应的人工地震波，按照新规范规定的材料动态性能参数取值的条件下，采用地震超载的方式进行高拱坝-地基系统的极限抗震承载能力研究，在寻求典型部位的变形随地震作用加大而变化的曲线上出现拐点作为系统整体安全判据的同时，关注坝体-地基系统从局部到整体的变形发展状况，建立安全判据的量化指标与其强震破坏发展过程中重要的物理变化之间的关系，从而明确该拱坝-地基系统在给定的整体稳定计算模式下的破坏机理，为确保大坝抗震安全提供参考。

1 计算方法概述

在计算分析中采用非线性地震波动反应分析方法，将坝体、地基和库水的强震反应本质上作为满足体系中接触面边界约束条件的波传播问题，在时域内以显式有限元方法求解。以黏弹性人工边界反映远域地基的辐射阻尼作用，以动接触力模型模拟坝体横缝、基岩各块体之间的缝面的接触滑移关系，在静力荷载作用后，考虑地震波输入进行有限元时程分析。

由于在结构为非线性的条件下，静、动力反应的叠加原理不成立，因此采用静动组合计算的方法，即将静力荷载以阶跃函数的形式施加到拱坝和地基系统上，以动力方法进行计算，待静力反应稳定后，再将地震波由基岩输入，对系统进行波动反应分析。

计算中，将两岸坝肩按地质构造确定的可能滑动岩块的各个滑动面，都作为抗剪强度符合Cou-lomb公式的、类似坝体横缝的接触面处理。由于在强震作用下，由于坝体横缝的张开，拱坝静动综合的最大主应力一般以拱端位置最为显著，易导致开裂，是拱坝坝体抗震的薄弱部位，即使在静态荷载作用下，沿拱座坝基的上游坝踵常为高拉应力区，中部为高剪应力区，且这一位置又是坝体和地基体系中的断面突变区，在施工中也为强约束区。为此，在沿坝基交接面这一薄弱部位设置双节点的动接触边界，但其初始抗拉强度在静、动荷载作用阶段分别取为混凝土的静、动态极限抗拉强度值。

在这一计算体系下，考虑由于地震本身存在很大不确定性而实际可能发生的超设计概率水平的地震动作用，即采用地震超载的方式大坝-地基体系达到整体安全的极限状态，基于对拱坝工作机理的认识以及参照Pacoima拱坝的震害实例，影响拱坝体系整体安全性的极限状态，是包括坝体和坝肩岩体在内整个体系的失稳，可取计入坝体和坝肩岩体动态变形耦合影响的坝体位移响应的突变和不断增长作为其相应的评价指标。

2 计算条件及计算模型

2.1 计算条件

作为算例的某拱坝为抛物线双曲拱坝，最大坝高285.5m，顶拱拱冠处厚14m，拱冠梁底厚60m，厚高比0.21。坝顶中心线弦长602.2m，弦高比2.17。上游正常蓄水位1880m，相应下游水位1640m；静荷载包括坝体自重、库水静水压力、淤沙压力、温度荷载、渗透压力。设计地震峰值加速度为355gal，地震输入采用设定地震方法生成场地相关设计反应谱，并依据场地相关反应谱生成人工地震加速度时程，三方向归一化的加速度时程如图1所示。

大坝坝区河谷陡峻，坡面完整，无大冲沟分布，坝基两岸分布有基本呈水平向的层间、层内错动带，这些错动带与基岩内优势裂隙切割出两岸多层滑块，可能对大坝地震动力响应及坝肩岩体动力稳定有一定影响，同时为提高大坝承载能力，在下游面拱端处设置了贴角，这些因素对大坝抗震安全的影响均需在计算模型中予以反映。

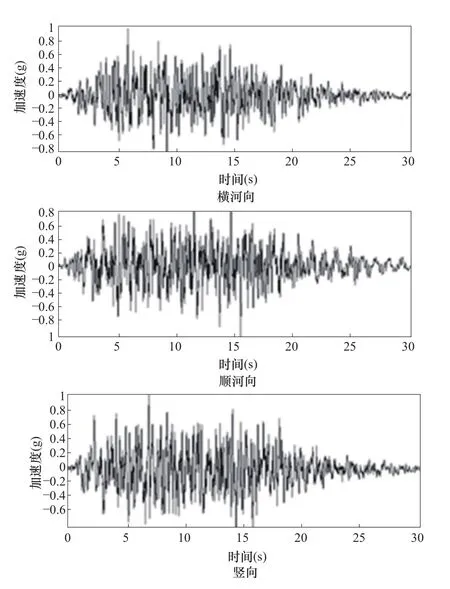
图1 输入地震加速度时程Fig.1 The input seismic acceleration time history

2.2 计算模型

对于该工程拱坝-地基系统计算分析采用基于空间域以集中质量有限元离散，时间域以中心差分法离散的数学模型，远域地基的能量逸散以黏弹性人工边界体现，坝体横缝和基岩内滑裂面及坝基交界面均以动接触力模型模拟，坝基交界面考虑初始抗拉强度。其数值按前期进行的大坝全级配动态性能试验结果取值，初始静态抗拉强度值为2.40MPa，初始动态抗拉强度值为3.65MPa。

根据该大坝坝区地形地质特点和坝区各类基岩材料性质，结合层间层内错动带以及拱端贴角的模拟要求，应用有限元网格自动剖分技术，生成大坝-基础系统三维有限元网格，坝体用沿厚度方向布置3层的三维块体元离散。整个分析系统顺河向为1120m，横河向1500m，竖向860m，节点总数57326，自由度数近171978个。拱坝-地基系统有限元网格如图2所示，其中坝体与滑块部分有限元网格如图3所示，由于层间层内错动带的切割，两岸块体均被分为6层（由图中滑块内不同颜色区分），由上至下所模拟的错动带及其位置和抗剪断参数列于表1。

图2 拱坝-地基系统有限元网格图Fig.2 The dam-foundation finite element mesh

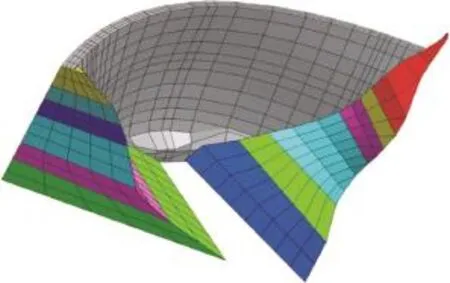
图3 坝体及两岸滑块有限元网格图Fig.3 The dam and sliders mesh

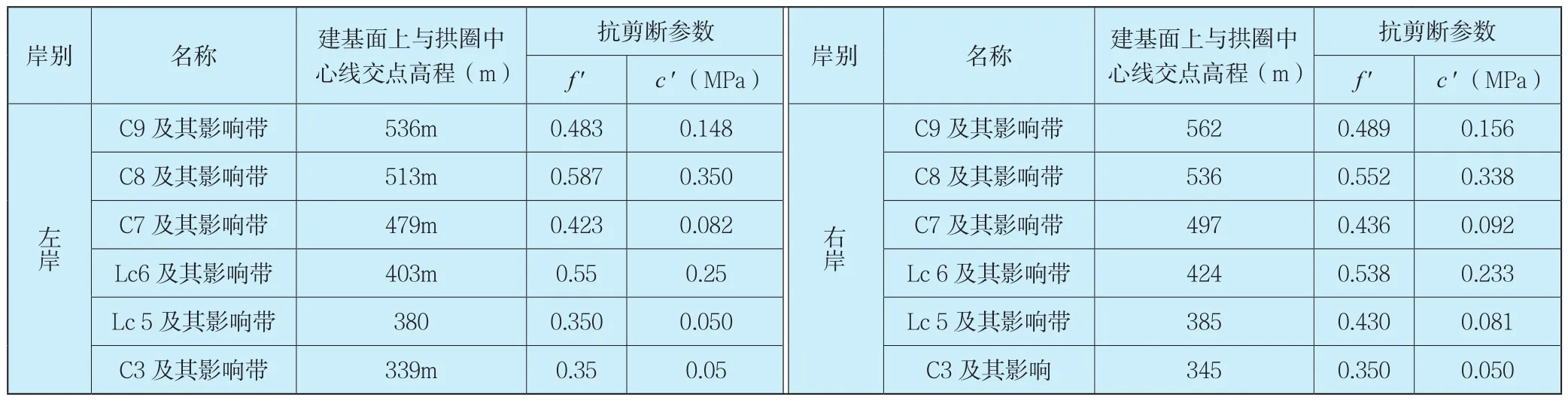
表1 两岸滑块内层间层内错动带位置及参数Tab. 1 The position and parameters of the disturbed belt in the slider

本文将按照反应谱生成的人工地震波作为地表输入，按照一维波入射时地表反应是底部输入2倍的理论解，将地震波折半作为人工边界处的地震加速度输入波，并利用专门程序将加速度波转换成位移波和速度波进行输入。坝体-库水的动力相互作用是影响大坝动力反应的重要因素。目前工程界普遍接受忽略库水可压缩性的所谓“库水附加质量”的处理方法表征动水压力的影响。本文分析中采用Westgarrd库水附加质量公式，折半后施加于坝面相应节点。

由于在计算中计入了基岩中的层间层内错动带等非线性接触面，整个体系的求解是一个非线性的动力分析问题，地应力场对应的基岩内动接触边界的初始应力状况必须计入，但地应力资料较难获得，本研究近似以地基自重应力场作为初始地应力场。所以其计算步骤分为三步：①首先对整个体系在未建坝时在近域地基自重荷载作用下进行静力求解，但仅保留地基内滑裂面的动接触边界间的接触力，作为接触边界初始状况，而将其初始滑移和张开度都置为0。②在此基础上，将建坝后坝体自重、库水压力、库内泥砂压力、温度、基岩渗压荷载等各项静力荷载以阶跃函数形式作用在整个计算体系，求解静力反应。③在静力求解稳定后，从人工边界底部入射三分量的地震位移时程，求解整个体系的地震波动反应。

在动态分析中，体系阻尼取瑞雷阻尼形式，α、β系数由体系阻尼比ξ=0.05及体系的有效高、低频范围确定。

2.3 计算工况

本研究考虑正常蓄水位与设计温降组合工况，在输入给定的场地相关的地震波时程的条件下，进行设计地震及在设计地震基础上，超载倍数为1.4、1.6、1.62、1.7、1.74、1.75、1.8的计算。

3 主要计算成果

经计算分析，图4和图5给出设计地震下右岸和左岸底滑面与上游坝面交界处坝体与基岩顺河向错动时程；图6给出设计地震下大坝建基面震后顺河向错动量分布；图7为两岸滑块震后顺河向位移云图；图8～图11为地震超载倍数为1.60、1.62、1.74、1.75时大坝建基面震后顺河向错动量分布；图12和图13为地震超载倍数为1.60与1.75时两岸滑块底滑面顺河向震后错动量分布；图14为坝踵震后顺河向位移随超载倍数变化曲线；图15为左右岸底滑面坝体基岩节点对震后顺河向错动随超载倍数变化曲线。

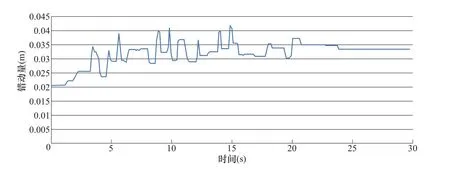
图4 设计地震右岸底滑面与上游坝面交界处坝体与基岩顺河向错动时程图Fig.4 Slip along the river at the junction of right slipping surface and the dam under design seismic

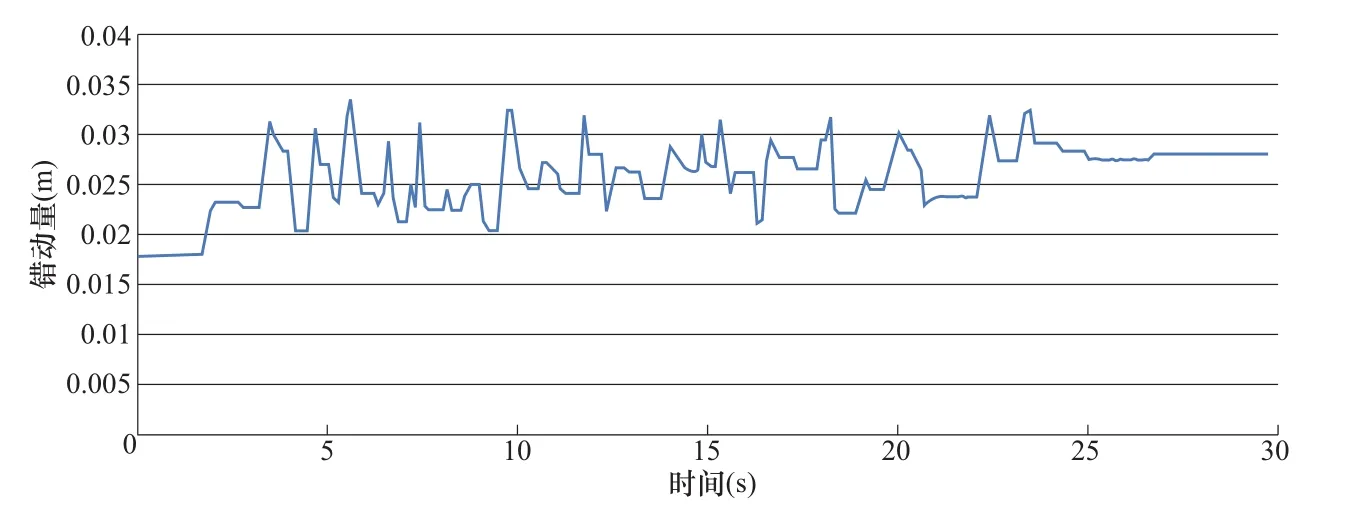
图5 设计地震左岸底滑面与上游坝面交界处坝体与基岩顺河向错动时程图Fig.5 Slip along the river at the junction of left slipping surface and the dam under design seismic

图6 设计地震建基面震后顺河向错动量分布图（cm）Fig.6 Distribution of the dislocation along the river for the dam-foundation interface（K=1.0）

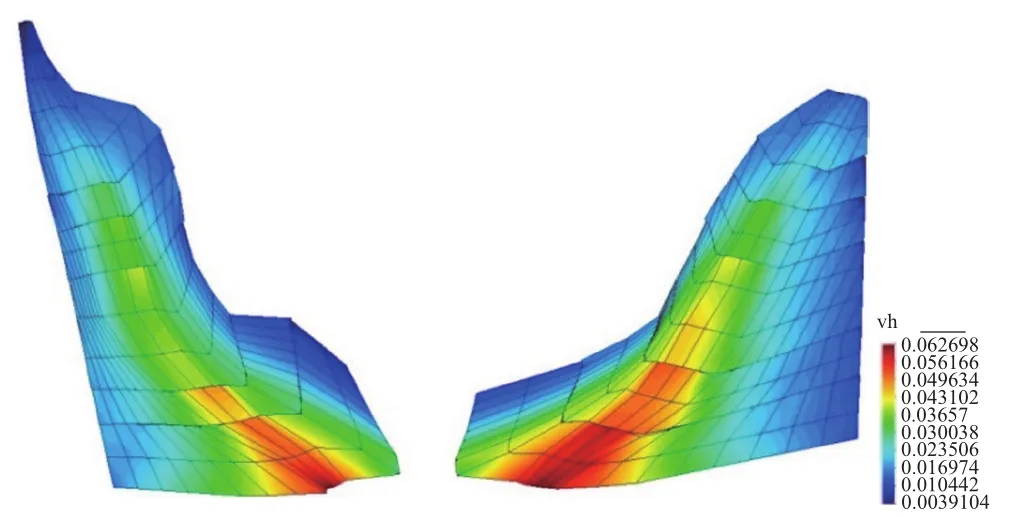
图7 设计地震两岸滑块震后顺河向位移云图（m）Fig.7 Distribution of the displacement along the river for the sliders（K=1.0）

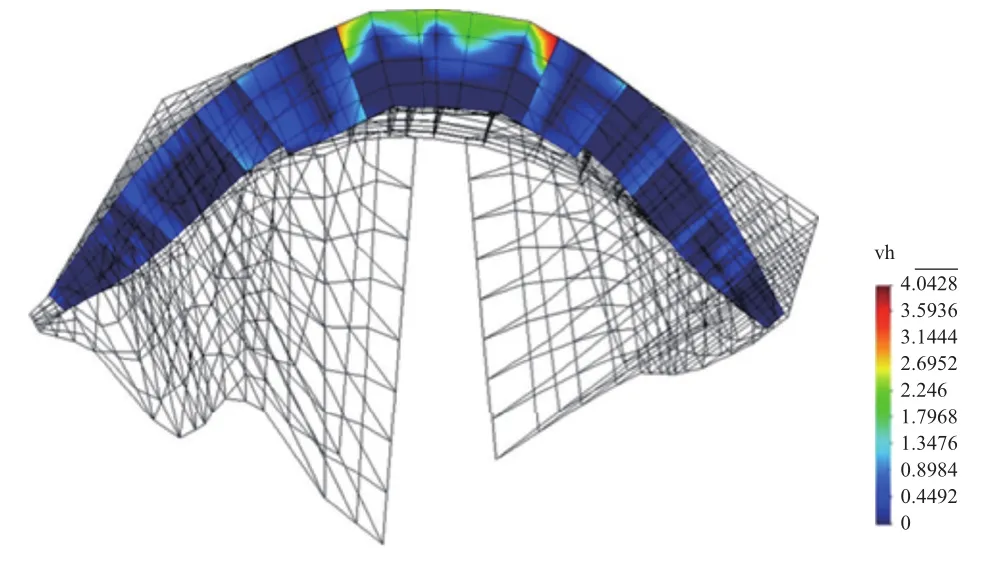
图8 建基面震后顺河向错动量分布（K=1.60）（cm）Fig.8 Distribution of the dislocation along the river for the dam-foundation interface（K=1.60）

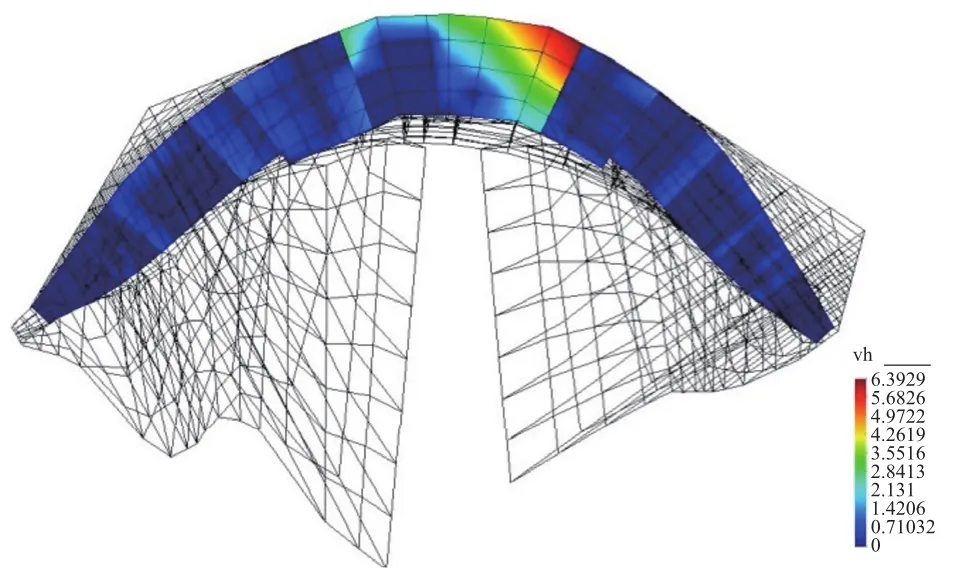
图9 建基面震后顺河向错动量分布（K=1.62）（cm）Fig.9 Distribution of the dislocation along the river for the dam-foundation interface（K=1.62）

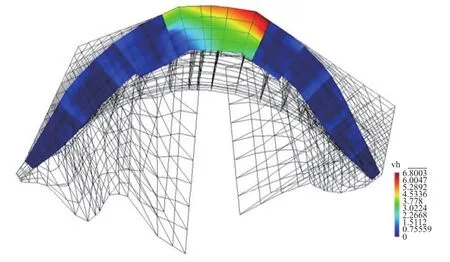
图10 建基面震后顺河向错动量分布（K=1.74）（cm）Fig.10 Distribution of the dislocation along the river for the dam-foundation interface（K=1.74）

图11 建基面震后顺河向错动量分布（K=1.75）（cm）Fig.11 Distribution of the dislocation along the river for the dam-foundation interface（K=1.75）

图12 滑块底滑面顺河向震后错动量分布（K=1.74）（cm）Fig.12 Distribution of the dislocation along the river for the bottom slipping surface（K=1.74）

图13 滑块底滑面顺河向震后错动量分布（K=1.75）（cm）Fig.13 Distribution of the dislocation along the river for the bottom slipping surface（K=1.75）

图14 坝踵震后顺河向位移随超载倍数变化曲线Fig.14 The relationship between the displacement of the dam heel and the overload factor curve

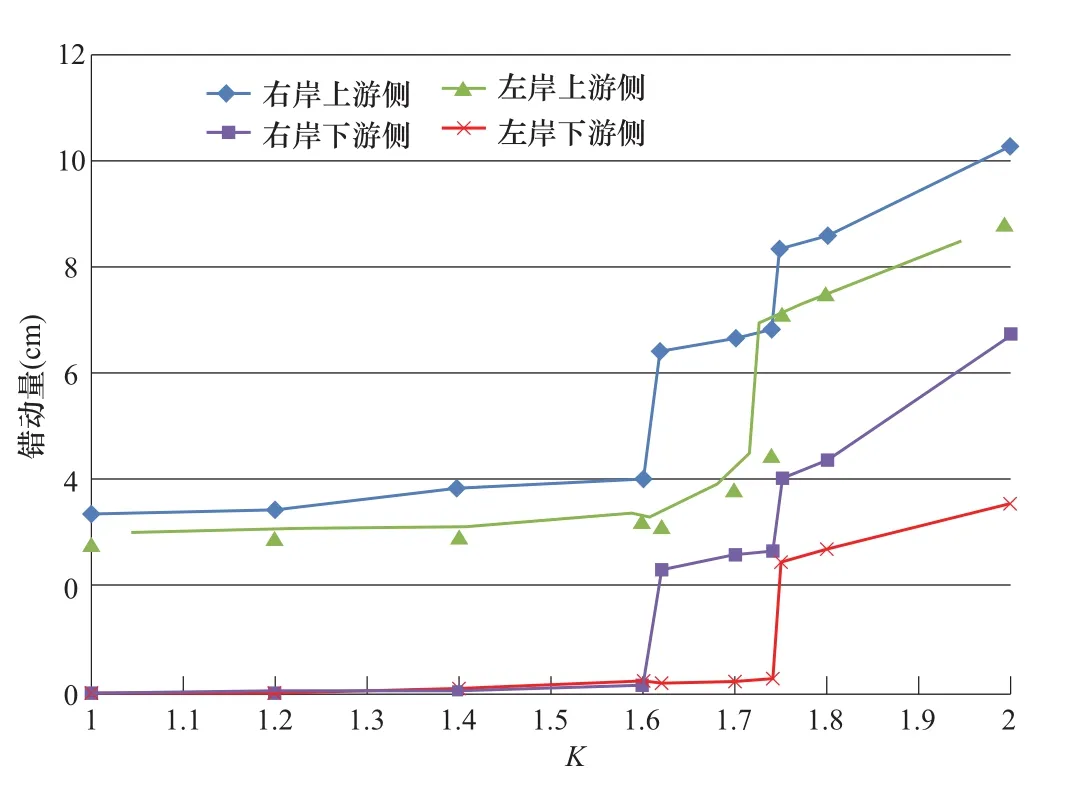
图15 左右岸底滑面坝体基岩节点对震后顺河向错动随超载倍数变化曲线Fig.15 The relationship between the sliding of the slider and the overload factor curve

4 破坏机理分析

从图4和图5两岸滑块底滑面高程处坝基交界面的局部错动时程曲线可见，在静态荷载作用下，两岸滑块底滑面与坝体上游面交界处坝体与基岩间出现1～2cm的局部错动，但在下游侧未发生错动。在设计地震过程中，底滑面上游侧的错动量有所增加，并在地震接近结束时达到稳定不再发展，而此时下游侧坝体与基岩间仍未发生错动。图6显示河床部位坝基交界面在上游侧出现错动，主要发生在上游侧略少于1/3坝厚的区域，而坝体与滑块间的错动主要发生在两岸滑块底滑面（C3）附近。由图7可见，滑块的顺河向位移量由底滑面向上呈由大到小的变化趋势，即最底层滑块残余顺河向位移最大。而随高程增高，滑块的顺河向位移减小，坝体与滑块间的错动渐不显著。总体上看，由于中上部两岸坝肩错动带的局部变形以及坝体横缝张开导致拱向作用降低，河床部位坝基承担了更多梁向静动荷载，地震过程中坝基上游侧发生了一定的局部错动。

由左、右岸底滑面与上、下游坝面交界处坝体与基岩顺河向错动随地震超载倍数增加的发展状况可见，如图8所示，在超载倍数为1.60及之前的地震工况，上游侧坝体与基岩间的错动量的增长随地震超载倍数的增加十分缓慢，下游侧节点对之间的错动量仅为2mm以下，大坝地基系统的工作性能未出现明显改变。在地震超载倍数为1.62时，如图9所示右岸底滑面部位坝体与基岩间发生贯穿性的剪切错动。右岸底滑面位置坝体与基岩间剪切错动区域的贯穿为相应区域大坝位移量的增长提供了运动学上的可能性。进而在超载倍数1.74时，如图10所示河床部位坝基交界面的明显错动区域虽已发展到该区域3/4以上的面积，但左岸底滑面处下游侧坝体与基岩间仍基本未发生错动。在超载倍数1.75时，如图11所示，左岸底滑面处坝体与基岩间也发生贯穿性的剪切错动，从而使滑块以下的整个河床部位坝基交界面均出现了贯穿性错动区域，致使坝体下部高程整体发生较大的顺河向位移。

如图12和图13所示两岸滑块底滑面C3的顺河向错动分布情况可见，底滑面在紧邻坝体的部位有较明显的错动，而在错动带内离开坝体一定距离处明显减小，底滑面在靠近侧滑面处基本未发生滑移，表明即使在较大的超载倍数下，滑块的变形主要限于层间层内错动带临近坝体区域的局部错动，未发生沿底滑面的整体滑移。

从破坏机理来看，由于两岸坝肩层间层内错动带局部变形和坝体横缝张开导致大坝拱向作用降低带来的拱端推力的减小，加之两岸侧滑面相对有利的产状和较强的抗剪参数，本文模拟的大坝两岸坝肩滑裂体具有较强的整体动力抗滑稳定性。相对而言，河床部位坝基交界面成为大坝-地基体系强震破坏的关键控制部位，随着地震超载倍数的增加，较弱的拱向作用使坝体承受的静动作用较多地向梁向转移，加剧了河床部位坝基面局部变形的发展，最终导致这一区域坝基面的剪切错动贯通，顺河向位移增长加速，而使大坝工作性态发生转折性变化。由这一拱坝-地基体系破坏模式和破坏机理的分析可见，设计所采用的下游贴角增大了河床坝段坝体的梁向刚度，扩大了河床部位的坝基交界面面积，对于延缓这一区域坝基面剪切错动的贯通，提高大坝的抗震承载能力是有利的。

图14可见坝踵节点顺河向位移在地震超载倍数超过1.60后，增加速度开始加快，在超载倍数达到1.74倍后，增速进一步加快，在超载倍数1.75时，震后位移达到12cm左右。从图15坝体与基岩间的局部错动随地震超载倍数增加的变化情况也可见，1.60和1.74是左右岸下游侧坝基交界面出现错动的分界点，因此在这两点处上下游的坝基交界面均出现两次阶跃性的增长，标志着大坝-地基体系的工作性态发生明显的变化。从特征位移随超载倍数变化曲线出现拐点的判据来看，地震超载倍数在1.60～1.74的范围是坝体-地基体系工作性态发生变化的转折区段，按照偏于安全的原则建议该拱坝的抗震超载安全系数取为典型部位位移开始陡增的1.60，但超载倍数1.74后坝体特征位移反应才真正出现显著增长。由此可见，特征位移随超载倍数变化曲线出现拐点也对应着结构体系某一关键部位的变形累积达到某一界限，形成新的、允许更大位移量的变形机制。在本研究的大坝算例中即为滑块以外的河床部位的坝基交界面错动范围贯通，使坝基底部能够形成整体错动。

5 结束语

本文在按照规范NB 35047—2015采用场地相关的设定地震反应谱及相应的人工地震波，并按照其规定的材料动态性能参数取值的条件下，采用地震超载的方式进行拱坝-地基系统的极限抗震承载能力和地震破坏机理的研究。研究表明，从特征位移随超载倍数变化曲线出现拐点的判据来看，地震超载倍数在1.60～1.74的范围是该拱坝坝体-地基体系工作性态发生变化的转折区段，按照偏于安全的原则建议其抗震超载安全系数取为典型部位位移开始陡增的1.60。而从相应的破坏机理分析可见，地震超载倍数在1.60～1.74的区段正相应于河床部位坝基交界面错动范围贯通，使坝基底部能够形成整体错动的变化过程。由此可见，特征位移随超载倍数变化曲线出现拐点也对应着结构体系某一关键部位的变形累积达到某一界限，形成了新的、允许更大位移量的变形机制。对于不同大坝工程而言，其大坝体型、坝址地形、地质条件等都具有各自的特点，其相应的地震破坏模式和机理也各不相同，但如能建立极限抗震能力判据的特征位移随超载倍数变化出现拐点这一量化指标与大坝-地基体系变形机制变化之间的相互关系，则将更加有助于对大坝-地基体系抗震安全的监控和保障。

[1] 涂劲，李德玉，张翠然，王海波. 汶川地震中沙牌拱坝震情验证研究 [J]. 水利学报，2016，47(5): 656-662.TU Jin，LI Deyu，ZHANG Cuiran，WANG Haibo. Study on the verification of the seismic performance of shapai arch dam during wenchuan earthquake[J]. Journal of Hydraulic Engineering，47(5):656-662.

[2] 涂劲，李德玉，陈厚群，欧阳金惠.大岗山拱坝-地基体系整体抗震安全性研究[J].水利学报，2011，42(2): 152-159.TU Jin，LI Deyu，CHEN Houqun，OUYANG Jinhui. Study on integral seismic safety of Dagangshan Arch dam-foundation system [J]. Journal of Hydraulic Engineering，2011，42(2): 152-159.

[3] 涂劲，陈厚群，张伯艳. 小湾拱坝在不同概率水平的地震作用下抗震安全性研究[J].水利学报，2006，37(3): 278-285.TU Jin，CHEN Houqun，ZHANG Boyan. Seismic safety of high arch in xiaowan project under the action of earthquake with different exceeding probabilities[J]. Journal of Hydraulic Engineering，2006，37(3): 278-285.

[4] 廖振鹏. 工程波动理论导论[M]. 北京:科学出版社，2002.LIAO Zhenpeng. Introduction of wave motion theories in engineering[J]. Beijing: The Science Publishing Company，2002.

[5] NB 35047—2015. 水电工程水工建筑物抗震设计规范[S].Beijing:China Electric Power Press，2015.

[6] NB 35047—2015. Code for seismic design of hydraulic structures of hydropow er projects[S].Beijing:China Electric Power Press，2015.