LS-SVM在澜沧江水库群运行调度中的应用研究

王 超，李学辉，杨绍琼，雷 旭，吴子怡，谢 平

(1.云南省水文水资源局，云南昆明650106；2.昆明市水文水资源局，云南昆明650103；3.武汉大学，湖北武汉430071)

随着经济社会的快速发展，对水库群的调度运行提出了越来越高的要求，中长期水文预报是进行水库调度的重要基础，在水资源的宏观调控、防汛抗旱等方面亦发挥着重要的参考作用。径流的中长期变化受太阳黑子活动、大气环流、自然地理、流域特性等诸多因素的综合影响，具有影响因子复杂、随机性极强的特点，模糊性、灰色性等多种不确定的属性，是一个复杂的高度非线性系统。中长期水文预报相对于短期水文预报来说，由于影响因子复杂，学术界尚未形成成熟可靠系统的预报方法，研究工作滞后于生产实际的要求。

现有径流的中长期预报理论，多从水文系列的统计相关特性着手研究，而对其物理成因研究尚在探索中；中长期水文预报模型众多，但缺乏一种普适型的模型满足不同地区和不同水文序列，不同的模型其适用性大相径庭。从预报方法看，较为传统的有多元回归分析、逐步回归分析、自回归模型、灰色模型等方法，近年来很多学者就人工神经网络、支持向量机最小二乘法、遗传规划、季节性水平模型等方法也进行了很多研究。其中，支持向量机最小二乘法(LSSVM)具有收敛速度高、非线性拟合能力强的特点[1-5]；季节性水平模型对径流序列进行中长期预测也具有一定的精度[6- 8]。因此本文运用支持向量机最小二乘法模型对澜沧江月径流序列进行预测，并与季节性水平模型预测结果进行比较，以探讨两种模型在澜沧江月径流预报上的适应性。

1 方法、模型

1.1 支持向量机最小二乘法(LS-SVM)基本原理

Suykens等学者于1999年提出最小二乘支持向量机，是以标准SVM的为基础一种改进算法，它不仅具有支持向量机泛化能力强、全局最优等优点，而且采用等式约束代替标准SVM的不等式约束，把向量机的二次规划问题转化为线性方程组问题，抗干扰能力明显提高，计算求解速度快，降低了计算求解的复杂程度[9-14]。

设训练集样本T={(xk，yk)|k=1，2，3…，n}xk∈Rn，yk∈R，xk是输入值，yk是输出值。构造的最优决策函数为

f(x)=ωTφ(x)+b

(1)

式中，ω为权向量；b为偏置量。

按照结构风险最小化的原理，将最优化问题转换为寻求最小目标函数f(x)

(2)

式中，γ为惩罚系数，表示对超出误差e的试验样本的惩罚权重，γ为可调参数；φ(x)为核空间映射函数；j(ω，e，b)为损失函数。

为推求ω和e，采用拉格朗日乘子法来求解这个二次规划问题，函数的定义：

(3)

式中，ai≥0(i=1，2，…，M)为拉格朗日乘子。

利用KK最优化条件对上式进行优化可得

(4)

整理可得到以下线性方程：

(5)

z=[φ(x1)T;…，φ(xn)T]，y=[y1；…；yn]，1v=[1；…；1]，α=[α1；…；αn]

令Ω=ZZT+γ-1I则a和b的表达式为：

a=(y-b1v)Ω-1

(6)

(7)

映射函数φ(x)与核函数K(，)存在着以下关系：

K(xi，xj)=φ(xi)Tφ(xj)

(8)

则最小二乘支持向量机的拟合函数可表示为：

(9)

核函数的参数选择影响着模型的精度，核函数的参数越多对模型预测的精度以及预测的速度越不利，本文选取高斯径向基核函数，表达式为：

(10)

式中，η应为核参数。

1.2 季节性水平模型

如果一个时间序列具有明显的季节性变化，而且各季节不同周期平均值相对稳定，则具备季节性水平模型的特点，适用季节性水平模型开展预测。模型中时段T的期望值为

μT=μρT

(11)

μ为各时段平均水平，ρΤ为时段T的季节比，季节比总是大于或等于零，平均值在同一个周期内是1。且满足

(12)

式中，M为一个周期划分的时段数。

首先利用历史时间序列对μ和ρΤ估计值进行推求，即可进一步推求出未来时段的预测值[15]。

为建立模型必须拥有至少两个全周期的时间序列资料，时间序列个数的数目T必须是M的倍数。N表示历史资料数据所包含的周期数，即N=T/M。T个时间序列按周期划分成N组，如下:

x1,x2,Λ,xM第一周期数据

xM+1,xM+2,Λ,x2M第二周期数据

…

x(N-1)M+1,x(N-1)M+2,Λ,xNM第N周期数据

根据上列数据得到M+1个估值如下:

(1)求各个周期的平均值

(13)

(2)求第t时段的季节比

(14)

(3)求各周期内每个时段的平均季节比

(15)

(4)对每一周期内的季节比进行规范化处理，使其平均值等于1。

(5)按照文献[15]相关步骤求出预测值。

1.3 模型评价指标

根据水文情报预报规范，选取以下四个指标对模型精度进行评价：

(1)纳什模型效率系数

(16)

(2)水量平衡系数

(17)

(3)年均最大径流的相对误差

(18)

(4)年均最小径流的相对误差

(19)

式中，n为径流序列的长度，l为年份数；Qpt和Qot分别为t时刻的预测值和实测值；Qo是实测径流均值；Qpj，max和Qoj，max分别为第j年最大径流的预测值和实测值；Qpj，min和Qoj，min分别表示第j年最小径流的预测值和观测值。NS和WB越接近于1，表示模型效果越好；REmax和REmin越接近于0，表示模型对极大值和极小值模拟预测能力越好。

2 预测结果评价

溜筒江水文站是澜沧江进入云南的第一个水文站，开展月径流预测工作对下游的各梯级电站及各水利工程运行具有较为重要的参考作用。以该站1956年～1994年的实测月径流用于建模，并以1995年—1999年的实测月径流作为校验。经过对实测数据标准化处理后，运用两个模型分别进行训练和预报，逐月成果数据过多，此处以年为单位对误差进行统计分析，训练期和预测应用期的模拟预测误差见表1和表2，成果见图1～2。

图1 训练期模拟结果对比

图2 预测应用期预测结果对比

2.1 LS-SVM预测结果分析

LS-SVM模型在1956年～1994年共468个月的训练期内的平均误差为±19.4%，变动范围在±8.7%～±35.4%之间；最大径流误差平均为±22.3%，变动范围在±1.5%～±48.6%之间；最小径流误差平均为±8.8%，变动范围在±0.4%～±22.6%之间；汛期整体误差较枯期稍大。

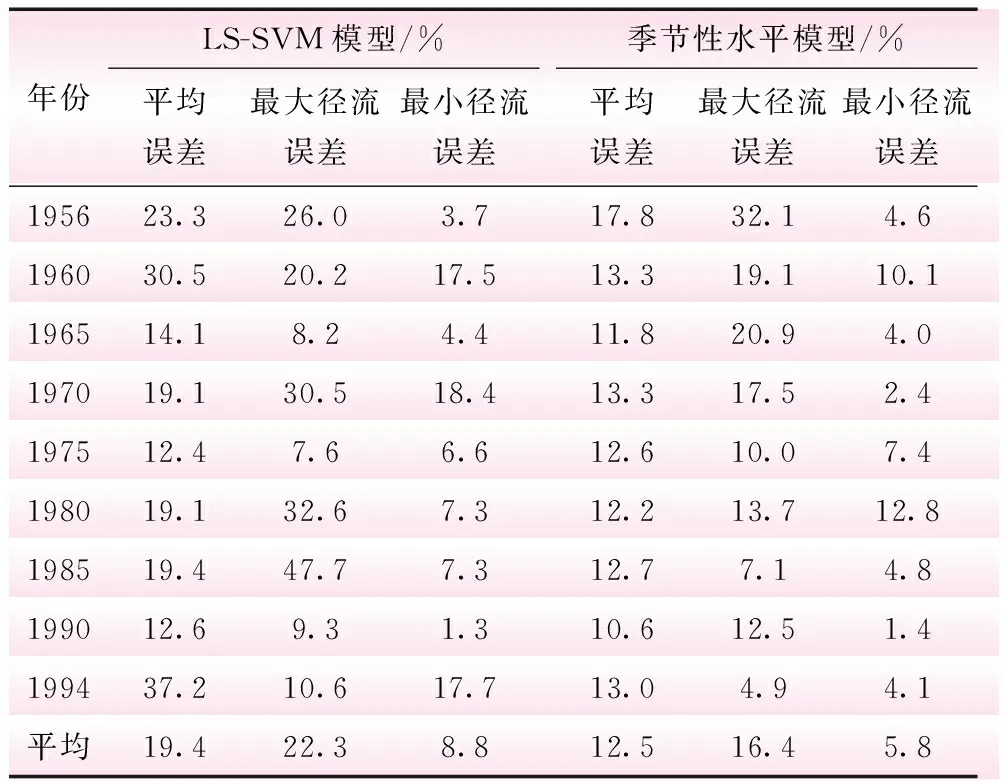
表1 训练期模型的模拟误差

在1995年～1999年共60个月的预测应用期，Ls-SVM模型平均误差为±17.9%，好于训练期，变动范围在±14.0%～±25.0%之间；最大径流误差平均为±9.5%，也好于训练期，变动范围在±2.3%～±25.7%之间；最小径流误差平均为±9.6%，与训练期相当，变动范围在±0.5%～±16.4%之间。

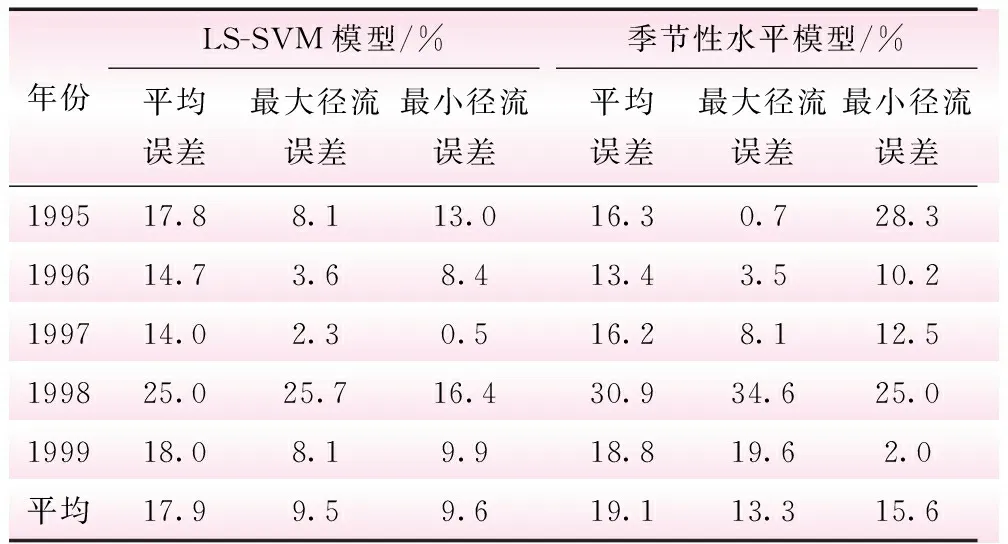
表2 预测应用期模型的预测误差

2.2 季节性水平模型预测及结果分析

季节性水平模型在训练期内的平均误差为±12.5%，变动范围在±7.2%～±16.2%之间；最大径流误差平均为±16.4%，变动范围在±1.4%～±38.4%之间；最小径流误差平均为±5.8%，变动范围在±0.5%～±17.4%之间；汛期整体误差较枯期也同样稍大。

在预测应用期内，季节性水平模型平均误差为±19.1%，略低于训练期，变动范围在±13.4%～±30.9%之间；最大径流误差平均为±13.3%，与训练期相当，变动范围在±0.7%～±34.6%之间；最小径流误差平均为±15.6%，误差比训练期稍大，变动范围在±2.0%～±28.3%之间。

2.3 两种方法对比分析

训练期和预测应用期的预测成果对比评价见表3。

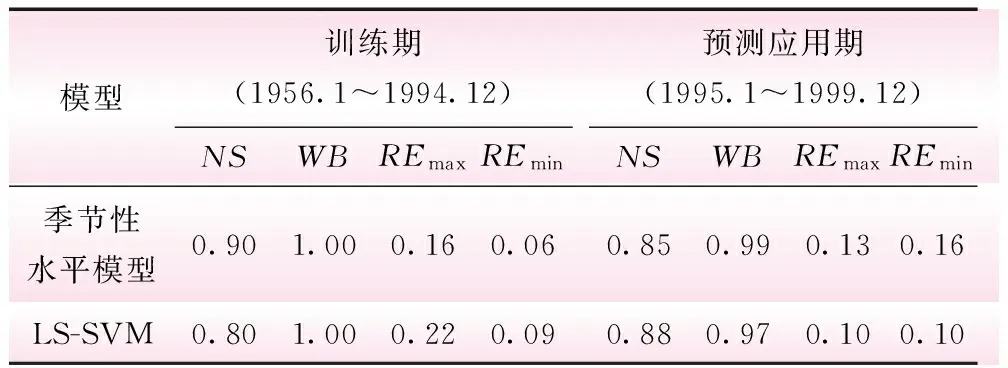
表3 训练期和预测应用期模型的模拟结果对比

根据表3分析，在训练期，季节性水平模型效率系数为90%，水量平衡系数为100%，年均最大和最小径流相对误差分别为16%和6%。LS-SVM模型效率系数为80%，水量平衡系数为100%，年均最大和最小径流相对误差分别为22%和9%。二者模拟效果均较好，季节性水平模型效率系数略高，年均最大和最小径流相对误差也略小，但总体差别不大。

在预测应用期，季节性水平模型效率系数为85%，水量平衡系数为99%，年均最大和最小径流相对误差分别为13%和16%。LS-SVM模型效率系数为88%，水量平衡系数为97%，年均最大和最小径流相对误差均为10%。季节性水平模型效率系数略高，而LS-SVM模型年均最大和最小径流相对误差更小，精度更高。

从图1～2可以直观地看出，季节性水平模型和LSSVM模型预测值与实测值的总体趋势一致，拟合过程符合性较好。预测应用期除1998年汛期的预测值与实测值偏差较大外，其他年份整体预测值与实测值符合性极高，对应性好，模型预测结果较好。

3 结 论

根据澜沧江域溜筒江水文站1956年～1999年的实测月径流资料，运用季节性水平模型和LS-SVM模型，对径流序列进行模拟和预测。经比较得到以下结论：

(1)在训练期，季节性水平模型与LS-SVM模型二者模拟效果均较好，季节性水平模型效率系数略高，年均最大和最小径流相对误差也略小，但总体差别不大。

(2)在预测应用期，季节性水平模型与LS-SVM模型二者模拟效果均较好，季节性水平模型效率系数略高，但LS-SVM模型年均最大和最小径流相对误差更小，精度更高。

(3)季节性水平模型与LS-SVM模型二者模拟效果均较好，均可满足澜沧江水库群调度的的需要，LS-SVM模型效果更佳。

参考文献：

[1] 巴欢欢, 郭生练, 钟逸轩, 等. SSA-LSSVM在中长期径流预测中的应用研究[J]. 水资源研究, 2016, 5(5)： 423- 433．

[2] WANG Yun, GUO Shenglian, CHEN Hua, H, et al. Comparative study of monthly inflow prediction methods for the Three Gorges Reservoir[J]. Stochastic Environmental Research & Risk Assessment, 2014, 28(3): 555- 570．

[3] 周轶成, 焦国军. 基于最小二乘支持向量机的马营河中长期径流预测研究[J]. 甘肃水利水电技术, 2014, 50(12): 1- 3．

[4] 刘冀, 王本德, 袁晶瑄, 等. 基于相空间重构的支持向量机方法在径流中长期预报中应用[J]. 大连理工大学学报, 2008, 48(4): 591- 595．

[5] 张卫国, 钟平安, 张玉兰, 等. 季节性支持向量机中长期径流预报模型[J]. 水力发电, 2014, 40(4): 17- 21．

[6] 孙传文, 钟平安, 万新宇, 等. 考虑季节因子的支持向量机径流预测模型[J]. 中国农村水利水电, 2014(4): 101- 104．

[7] 张潇, 夏自强, 黄峰, 等. 基于SSA-ARIM模型的青弋江干流径流预测[J]. 中国农村水利水电, 2015(3)： 6- 9．

[8] 李佳, 王黎, 马光文, 等. LS-SVM在径流预测中的应用[J]. 中国农村水利水电, 2008(5): 8- 10．

[9] 崔东文. 多隐层BP神经网络模型在径流预测中的应用[J]. 水文, 2013, 33(1): 68- 73．

[10] WU C L, CHUN K W. Rainfall-runoff modeling using artificial neural network coupled with singular spectrum analysis[J]. Journal of Hydrology, 2011, 399(3- 4): 394- 409.

[11] 汪芸, 郭生练, 李响. 奇异谱分析在中长期径流预测中的应用研究[J]. 人民长江, 2011, 42(9): 4- 7．

[12] SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293- 300．

[13] 邵骏, 袁鹏, 张文江, 等. 基于贝叶斯框架的LS-SVM中长期径流预报模型研究[J]. 水力发电学报, 2010, 29(5): 178- 182．

[14] 林剑艺, 程春田. 支持向量机在中长期径流预报中的应用[J]. 水利学报, 2006, 37(6): 681- 686．

[15] 赵国杰, 张光锦, 赵新波,等. 基于季节性水平模型的中长期径流预测[J]. 海河水利, 2007(5): 37- 40．

[16] 苏欢, 董晓华, 方燕琴. SWAT在淮河上游地区径流模拟中的应用研究[J]. 人民长江, 2016, 47(8): 18- 28．