基于多目标遗传算法的Σ-Δ MEMS加速度计优化设计*

王梦醒， 刘 丹， 熊兴崟， 李宗伟， 韩可都

(1.中国科学院 地质与地球物理研究所 中国科学院油气资源研究重点实验室，北京 100029； 2.中国科学院大学，北京 100049)

0 引 言

Σ-Δ闭环力反馈微机电系统(micro-electro-mechanical system,MEMS)加速度计不仅可以实现高精度模/数转换，还能够获得较好的带宽、动态范围和线性性能[1～4]。高精度的MEMS加速度计需要在环路滤波器中级联积分器构成高阶Σ-Δ闭环力反馈系统，但高精度和稳定性难以同时满足。遗传算法[5](genetic algorithm,GA)已应用于MEMS加速度计敏感元件参数设计[6]及Σ-Δ MEMS加速度计系统设计[7～8]，但缺少对闭环系统稳定性的考虑，设计的系统往往不是最优。

为此，本文提出并采用了多目标遗传算法对高阶Σ-Δ MEMS加速度计环路滤波器参数进行优化设计，该算法将信噪比和∞—范数作为设计目标。相比传统单目标遗传算法设计目标只有信噪比，本文算法在确保高信噪比的同时，提高了系统的相位裕度，使得最大稳定输入信号范围增幅超过1倍，并增强了系统对MEMS敏感元件工艺误差的鲁棒性。

1 设计原理

高阶Σ-Δ MEMS加速度计的系统框图如图1所示[9]。

加速度计中的MEMS敏感元件工作于欠阻尼状态时，在Σ-Δ闭环系统中，环路滤波器设计的2个目标为增强噪声整形能力和提高闭环系统的稳定性。为了解决由于前置补偿器引入的额外极点而影响系统的噪声整形效果的问题，本文采用非限定性Σ-Δ MEMS加速度计，非限定性结构具有足够的自由度设计闭环系统传递函数的所有极点以维持系统的稳定性而无需添加前置补偿器[10,11]。

图1 高阶Σ-Δ MEMS加速度计系统框图

以三阶非限定性Σ-Δ MEMS加速度计为例，其等效线性模型如图2所示。

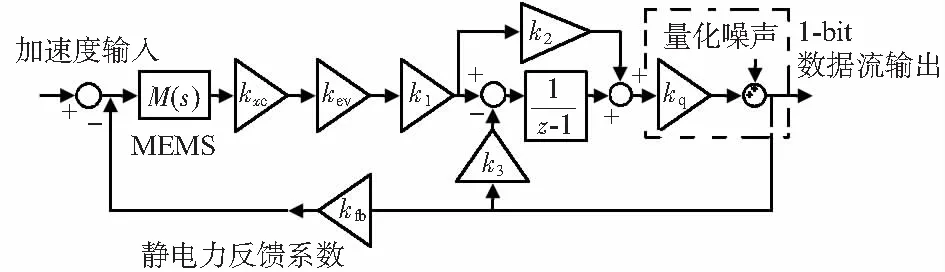
图2 三阶非限定性Σ-Δ MEMS加速度计等效线性模型

由图可推导出量化噪声传递函数(noise transfer function,NTF)为

(1)

式中Hm(z)为敏感元件离散时间域传递函数；kxc为位移—电容比例系数；kcv为电容—电压比例系数；k1,k2,k3为环路滤波器参数；I(z)为积分器传递函数；kfb为静电力反馈系数；kq为量化器近似等效增益，由仿真得到的量化器输入值y和输出值v确定[12]即

(2)

Σ-Δ MEMS加速度稳定性，必须满足带外噪声增益不能过大，因此，选择噪声传递函数的∞—范数作为调节系统稳定性的参数[13]，∞—范数定义为

‖NTF‖∞=max|NTF(ejω)|

(3)

式中 max|NTF(ejω)|为噪声传递函数在所有频率上的最大增益，一般选择∞—范数小于1.5[13]。

2 基于多目标遗传算法的环路滤波器优化设计

本文采用的多目标遗传算法设计流程如图3所示，算法具有2个目标函数值：由输出比特流的功率谱密度计算得到的信噪比和噪声传递函数的∞—范数。

图3 多目标遗传算法流程

初始种群中的个体在参数设定范围内采用浮点数编码随机产生，计算每个个体的信噪比和∞—范数并求得相应适应度，再计算总适应度。每代根据个体总适应度选择种群中的个体进行交叉、变异操作。为加速收敛过程，确保每代最优个体能遗传到下一代，保留原种群中的部分优秀个体，和经过交叉、变异操作后形成的新个体一起组成新种群，种群更新比例为0.9。

为避免算法陷入局部最优，个体适应度f由目标函数值的排序确定，其公式如下[13]

(4)

式中N为种群中个体数量;P为个体按照目标函数值排序后的位置，信噪比最高和∞—范数最小的个体分别对应最大的适应度。多目标遗传算法采用权重系数变换法，总适应度函数为[14]

fT=w1·f1(SNR)+w2·f2(‖NTF‖∞)

(5)

式中w1,w2为权重因子。

3 系统仿真分析

搭建三阶非限定性Σ-Δ MEMS加速度计的Simulink模型，如图4所示，分别采用本文的多目标遗传算法和传统单目标遗传算法对环路滤波器参数k1,k2,k3进行搜索。选择环路滤波器k1,k2,k3共3个参数的范围分别为[0.1,50]，[0.1,50]，[0.1,10]。搜索终止条件为进化代数，综合考虑计算效率和种群多样性，选择种群个体数为60个，进化代数为25代。

图4 三阶非限定性Σ-Δ MEMS加速度计Simulink模型

为了更好地说明多目标遗传算法的优势，本文在4个方面对2种算法的搜索结果进行对比仿真分析:

1)遗传进化特性对比。图5给出了2种算法的历代种群中个体的平均信噪比和最优信噪比的仿真结果。图5(a)所示单目标遗传算法平均信噪比始终波动较大，而图5(b)所示多目标遗传算法的平均信噪比在16代后趋于稳定，具有更好的遗传进化特性。

图5 历代搜索结果

2)最后一代个体的∞—范数对比分析。如图6，单目标遗传算法得到的最后一代个体的∞—范数平均值约为3.2，而多目标遗传算法得到的最后一代个体的∞—范数平均值约为1.3，可见多目标遗传算法设计系统的噪声传递函数增益得到了限制。

图6 最后一代个体∞—范数分布对比

图7为多目标遗传算法搜索得到的个体A和单目标遗传算法搜索得到的个体B的输出功率谱密度，个体A的信噪比为121.9 dB，个体B的信噪比为124.5 dB，可以看出2种算法都可以获得较高的信噪比。根据∞—范数定义计算得到个体A的∞—范数为1.41，个体B的∞—范数为3.18。

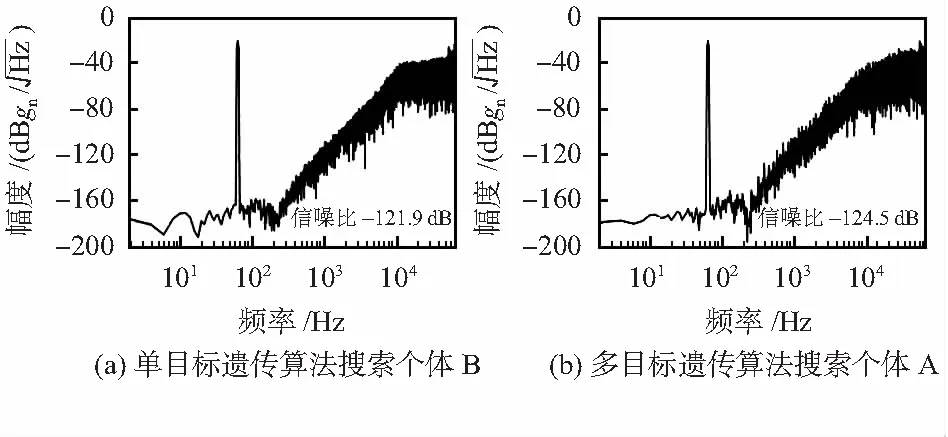
图7 功率谱密度对比

3)系统相位裕度对比分析。对比如表1所示，个体A的相位裕度为41.8°，个体B的相位裕度为18.7°，多目标遗传算法搜索得到的个体相位裕度明显提高，系统的稳定性具有较大改善。

表1 个体性能参数比较

4)系统最大稳定输入信号范围对比分析。图8为个体A与个体B的输入加速度和信噪比的关系。个体A的最大稳定输入信号约为0.4gn，个体B的最大稳定输入信号约为0.19gn，多目标遗传算法搜索得到的系统最大稳定输入信号范围增幅超过1倍。个体A与个体B的参数对比如表1所示，可见多目标遗传算法设计得到的系统信噪比虽略有降低，但系统稳定性明显提高。

图8 系统输入加速度和信噪比的关系

5)系统对MEMS敏感元件工艺误差鲁棒性对比分析。由于非限定性MEMS加速度计对敏感元件中的弹性系数较为敏感[12]，因此，将弹性系数变化范围设为±40 %进行鲁棒性分析。图9给出了个体A与个体B的鲁棒性分析仿真结果。对两个体的信噪比分别进行最小二乘拟合，由拟合曲线可以看出，与单目标遗传算法得到的个体B相比，随着弹簧系数变化增大，多目标遗传算法得到的个体A的拟合曲线下降更加缓慢，即个体A对弹性系数变化较为不敏感，有更好的鲁棒性。

图9 弹性系数变化与信噪比的关系

4 结 论

本文采用多目标遗传算法对高阶Σ-Δ MEMS加速度计环路滤波器参数进行优化设计，将∞—范数和信噪比同时作为设计目标。仿真结果表明：相比单目标遗传算法，多目标遗传算法提高了系统的相位裕度，使得系统最大稳定输入信号范围增加超过1倍，增强了对MEMS敏感元件参数偏差的鲁棒性。本文提出的方法同样适用于四阶及四阶以上的高阶系统的优化设计和其他结构Σ-Δ MEMS加速度计的优化设计。

参考文献:

[1] Navid Yazdi，Farrokh Ayazi，Khalil Najafi.Micromachined inertial sensors[J].Proceedings of the IEEE，1998，86(8)：1640-1659.

[2] José M，de la Rosa.ΣΔ modulators:Tutorial overview,design guide,and state-of-the-art survey[J].IEEE Trans on Circuits Systems I：Regular Papers，2011，58(1)：1-21.

[3] 李宗伟，杨 燕，熊兴崟,等.高精度电容式MEMS加速度计系统设计[J].传感器与微系统，2017，36 (6)：98-101，104.

[4] Vladimir P Petkov，Bernhard E Boser.High-order electro-mecha-nical Σ—Δ modulation in micromachined inertial sensors[J].IEEE Transactions on Circuits and Systems I:Regular Papers，2006，53(5)：1016-1022.

[5] 王小平，曹立明.遗传算法—理论、应用与软件实现[M].西安：西安交通大学出版社，2002：14-16.

[6] 王永泉，陈花玲，贺学明.基于遗传算法的静电反馈式微传感器多目标优化[J].西安交通大学学报，2006，40(11)：1305-1309.

[7] Reuben Wilcock，Michael Kraft.Genetic algorithm for the design of electro-mechanical sigma delta modulator MEMS sensors[J].Sensors，2011，11(10)：9217-9232.

[8] Kraft M，Wilcock R，Almutairi B.Innovative control systems for MEMS inertial sensors[C]∥IEEE International Frequency Control Symposium(IFCS)，2012：1-6.

[9] Liu Y T，Liu X W，Chen W P.Design and noise analysis of Σ-Δ capactive micro-machinned accelerometer[J].Journal of Semiconductors，2010，31(5)：1-6.

[10] 李 洋，黎晓林，吴 健,等.基于数字电路的二阶Σ-Δ调制微加速度计[J]. 传感器与微系统，2015，34 (1)：91-93.

[11] Johan Raman，Pieter Rombouts，Ludo Weyten.An unconstrained architecture for systematic design of higher order Σ-Δ force-feedback loops[J].IEEE Trans on Circuits Systems I：Regular Papers，2008，55(6)：1601-1614.

[12] Richard Schreier，Gabor C Temes.Understanding delta-sigma data converters[M].HoboKen，New Jersey:John Wiley & Sons，2006：97-100.

[13] 雷英杰，张善文，李续武,等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社，2005：74-76.

[14] 马小姝，李宇龙，严 浪.传统多目标优化方法和多目标遗传算法的比较综述[J].电气传动自动化，2010，32(3)：48-50.