函数型部分线性自回归模型在金融中的应用

王咪咪,丁 辉

(滁州学院 数学与金融学院，安徽 滁州 239000)

在金融交易市场中,常常会有在一个时间段内连续被记录的数据。譬如，在股指期货交易市场上，任意小的交易时间区间内都会产生交易，衍生出很多高频数据。高频数据可以看成一个时间区间内连续被记录的数据。因此,可视为函数型数据，函数型数据分析是分析和处理高频数据的必备利器。国内外已有一些学者在函数型数据视角下研究金融经济市场中的内在规律，也得到了一些宝贵研究成果。郭均鹏通过函数型主成分分析方法研究了Shibo市场中的各期限利率的波动问题[4]；刘春义等通过使用函数型聚类分析方法研究了我国经济发展的周期问题[7]；龙文等借助于函数型主成分分析探讨了不同国家之间的金融危机时期经济发展的差异性[8]；赵煜[10]在函数型数据分析视角下对生态经济系统的分析前景进行展望。然而，上述所有研究均无法刻画因变量的过去对其产生的影响。实际上，因变量的过去时刻常常会对其产生影响。因此，通过自回归的介入，在函数型线性的模型上加入自回归部分来刻画因变量的过去时刻的影响，即函数型部分线性自回归模型。该模型既能刻画函数型协变量与因变量之间的关系，又能表现因变量的过去时刻对当前时刻的影响。

1 函数型部分线性自回归模型

给出函数型部分线性自回归模型：

(1)

其中，X(t)是区间I上平方可积的函数型变量，Y是因变量，p是滞后阶数，误差项ε满足Eε=0,Varε=σ2。自回归模型为此模型的一个特例(β(t)≡0 )，函数型线性模型同样也为此模型的一个特例(φ1=…=φp=0)。

关于该模型的估计，我们采用剖面最小二乘估计[1]：

(2)

(3)

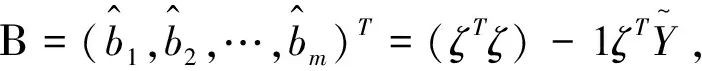
(4)

(5)

可以求出模型的参数φ1,…,φp和非参数函数g(·)的估计。

令Y=(Yp+1,…,Yn)T，Φ=(1,φ1,…,φp)T，W=ζ(ζTζ)-1ζT，Z0=(1,…,1)T(n-p)×1,Z1=(Yp,…,Yn-1)T,Z2=(Yp-1,…,Yn-2)T,…,Zp=(Y1,…,Yn-p)T，Z=(Z0,Z1,…,Zp)T，Y*=(I-W)Y,Z*=Z(I-W) ，I为n-p阶单位阵。于是(2.5)可化为(Y*-Z*TΦ)T(Y*-Z*TΦ)，则：

(6)

把(6)带回(4)得：

(7)

到目前为止，已经求得了模型参数的估计。然而，在求解模型的参数估计过程中必然会涉及到滞后阶数p的选取，统计模拟时采取交叉验证准则来选择p。

2 统计模拟

按照下面的模型来生成数据：

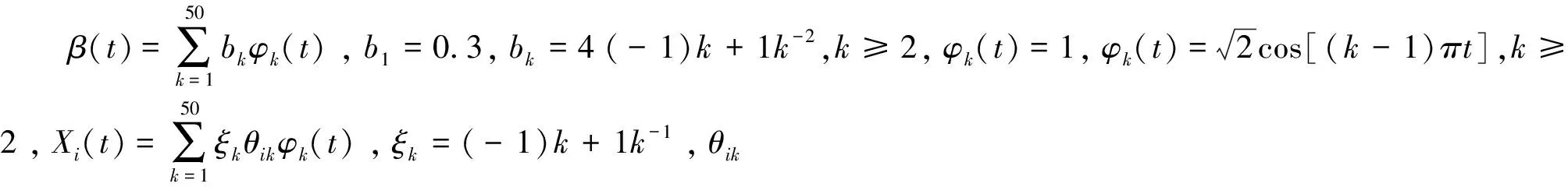
表1 估计均值和标准差(括号)或RASEs和标准差(括号)结果表

从表1可见，α,φ1,…,φ3估计偏差与估计标准差β(t)估计均方误RASE均随着样本量的增加而减少，因此，可以看出估计方法的优良性。

3 实证分析

选择2015年6月1日至2016年3月1日总共183个股市交易日的上证指数数据。模型的因变量为开盘价Y，函数型协变量为每个交易日每5分钟的上证指数X(t)，每个交易日每5分钟的数据共48个。首先进行预处理，对开盘价Y和每5分钟的上证指数X(t) 取对数，目标为寻找合适的模型对开盘价进行预测。显然，开盘价既受过去时期开盘价的影响，又与Xi(t)有关，考虑函数型部分线性自回归模型：

(8)

表2 不同模型及其相对应的平均预测误差(单位×10-5)

从表2可知，函数型部分线性自回归模型平均预测误差最小，比线性模型的预测效果提升了65.8%，比自回归模型的预测效果提升了97.6%。可见，函数型部分线性自回归模型拟合效果最好。

4 结语

函数型部分线性自回归模型既刻画了函数型协变量与因变量之间的关系，又考虑了自回归效应，体现了因变量过去时刻的影响，因而具有广泛的适用性，可为今后研究函数型数据提供一种新的工具。

参考文献：

[1] Härdle W,Liang H,Gao J. Partially linear models[M].New York: Springer，2000.

[2] Ramsay J O， Silverman B W.Functional Data Analysis[M].New York: Springer，1997.

[3] Ramsay J O,Hooker G,Graves S.Functional Data Analysis with R and MATLAB[M].New York: Springer，2009.

[4] 郭均鹏,孙钦堂,李汶华.Shibor市场中各期限利率波动模式分析：基于FPCA方法[J].系统工程,2012(12):88-92.

[5] 姜高霞,王文剑.经济周期波动的函数型时序分解方法：基于CPI的实证分析[J].统计与信息论坛,2014,29(3):22-28.

[6] 李敏.基于函数型主成分分析方法的用水量数据分析[J].合肥学院学报,2014，24(4):21-25.

[7] 刘春义,刘黎明,王少国.经济周期测算的新视角：基于函数型数据分析方法[J].调研世界,2015(6):42-46.

[8] 龙文,李楠,王惠文,等.金融危机过程中不同类型国家经济发展的差异性比较：基于函数数据分析方法[J].管理评论,2014,26(3):3-10.

[9] 米子川,赵丽琴.函数型数据分析的研究进展和技术框架[J].统计与信息论坛,2012,27(6):13-20.

[10] 赵煜,秦增举.函数型数据分析及其在生态经济系统中的应用展望[J].甘肃科技,2015,31(16):66-68.