城轨线路运营时段前车底空驶出场路径优化

钟庆伟， 赵 军， 文 超， 彭其渊(西南交通大学 交通运输与物流学院， 四川 成都 610031)

车底运用计划是城市轨道交通线路的基础行车组织计划之一，主要为提前绘制的运行图中的列车指派车底。城市轨道交通线路通常设置多个车场(包括车辆段和停车场)，并运行多条列车交路，列车的始发和终到站不一定为车场所在站，使得车底在全日存在出入场运行，包括运营时段前集中出场、运营时段内分散出入场和运营时段后集中入场。全日车底出入场运行不仅对运营时段内列车运行造成干扰，还在非运营时段特别是运营时段前产生大量的空驶距离。确定全日车底出入场运行路径及其在路径上的运行线是城市轨道交通线路车底运用计划编制的关键问题，目前现场计划编制人员往往凭借经验解决该问题，计划编制效率低下，且难以确保车底运用计划的质量。鉴于此，本文探讨城市轨道交通线路运营时段前车底集中空驶出场路径问题。

目前，国内外尚未关注过城市轨道交通线路在运营时段前的车底空驶出场路径问题，只在相关的运营时段内列车运行图和车底运用计划编制方面开展过一定工作。列车运行图编制方面，国外多考虑基于动态需求的城市轨道交通线路列车运行图编制。文献[1-2]以实际拥挤区段为对象，研究满足客流需求动态变化及车底快速周转的运行图编制模型与算法。文献[3]采用列车运行等效时间间隔概念，从3个不同的角度分别建立需求驱动运行图模型。文献[4-5]以旅客平均等待时间最小为目标，提出动态需求环境下的运行图编制模型与算法。国内对于城市轨道交通线路列车运行图编制的研究并不多。文献[6]以车场设置地点为核心，提出两站图及三站图理论并以此构建运行图通用数学模型。文献[7]重点研究共线交路运行图中车底运用、列车开行间隔等问题，并对其铺画流程和方法进行探讨。文献[8]基于现行运行图编制理论与方法，构建了共线交路运行图编制的双层规划模型。

第二项前期研究为车底运用计划编制，其与车底空驶出场路径问题关系更为密切。国外方面，文献[9-11]在考虑列车编组、车底解编、车底空驶和客流需求等的情况下，研究车底运用计划鲁棒性编制问题，以综合作业成本最低为目标建立车底运用优化模型，并采用Bender分解法求解模型。国内方面，文献[12]归纳共线交路的4种基本形式，分别建立车底独立与套跑运用条件下的优化模型，并开发通用的车底运用优化工具。文献[13]基于图论思想研究网络化运营条件下车底运用计划编制问题，并设计混合列生成算法求解所建立的车底运用优化模型。文献[14]建立了更为具体的车底运用优化模型，并根据模型特点开发并行禁忌搜索算法。

综上，未见文献探讨过城市轨道交通线路运营时段前车底空驶出场路径的优化方法。既有运行图编制的研究通常只侧重于优化运营时段内的运行线，即使理论上可将其拓展于编制运营时段前的车底空驶出场运行线，但由于其忽略多交路、多车场和集中出场等实际情况，难以获得运营时段前高质量甚至可行的车底出场运行线。同时，既有车底运用计划编制研究往往提前设定车底从车场到车站的出入路径，着重优化运营时段内的车底交路，未考虑运营时段前车底集中出场以及直达和折返两种灵活的出场路径，由车底交路勾画的出场路径很容易导致后续不能绘制出可行的车底出场运行线。因此，为提高城市轨道交通线路全日车底运用计划的编制质量，本文研究基础的运营时段前车底空驶出场路径优化方法，着重探讨具有多交路、多车场和多车型的车底空驶出场路径问题。

1 问题定义

1.1 问题描述

以含6个车站、2个车场和4个折返站的城市轨道交通线路为例，对所研究问题进行描述。如图1所示，车站沿上行方向依次编号为s1～s6。车站s2和s5分别为车场d1和d2所在站，区间A1为车场d1的后方，区间A2和A3为车场d1的前方，同理，区间A1和A2为车场d2的后方，区间A3为车场d2的前方。车站s1、s2、s4和s6为折返站，其中，车站s1和s2为上行折返站(可将列车由下行折返为上行)，车站s4和s6为下行折返站(可将列车由上行折返为下行)。假设线路采用2条列车交路l1和l2，交路l1的端点分别为车站s1和s4，交路l2的端点分别为车站s2和s6。线路6:30开始运营，运营时段初有2列列车i1和i2需要由车场始发的车底来担当。列车i1为下行列车，属于交路l1，分别始发和终到于车站s4和s1。列车i2为上行列车，属于交路l2，受运营开始时刻的限制，只始发于车站s3，并终到于车站s6。现需为该2列列车的车底指派配属车场及其对应的出场路径，以获得最小的空驶距离。

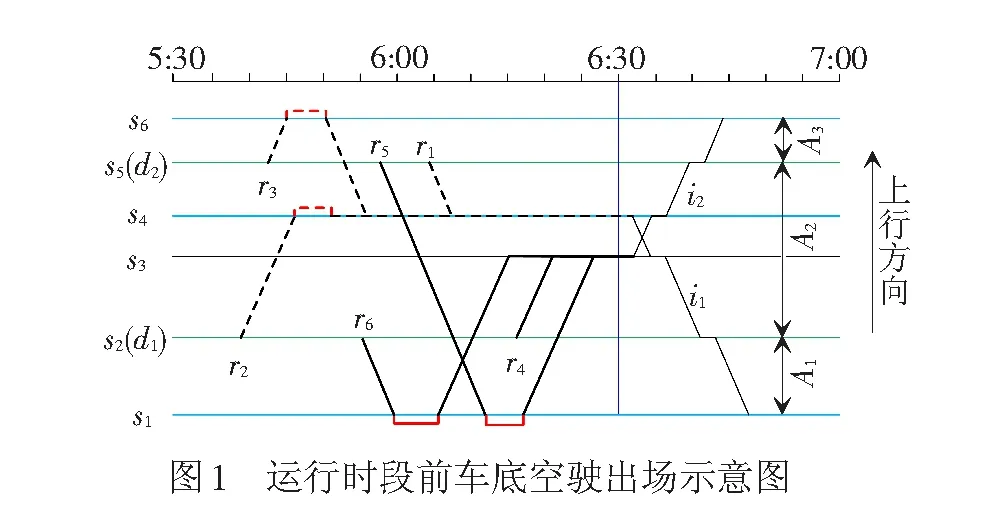
从图1可看出，若忽略车场与折返站的能力，则列车i1的车底可有3条空驶出场路径，如图中粗虚线所示。路径r1中，车底从车场d2出发，经出场线至所在站s5后，运行至列车i1的始发站s4，由于车站s5至s4的运行方向与列车i1的相同，无需折返。路径r2中，车底从车场d1出发，经出场线至所在站s2后，运行至列车i1的始发站s4，并在此从上行折返为下行，以满足列车i1的运行方向要求。路径r3中，车底从车场d2出发，经出场线至所在站s5后，首先运行至车站s6，在此折返后，再运行至列车i1的始发站s4。将路径r1称为直达路径，路径r2和r3称为折返路径。类似地，列车i2的车底也有3条空驶出场路径，分别为直达路径r4，折返路径r5和r6，如图中粗实线所示。车场的出车距离不同，折返站的折返距离也不同，使得各条出场路径可产生不同的空驶距离。直达路径的空驶距离往往比折返路径小，但受能力限制，直达路径并非总可行，为应对能力紧张，不得不采用折返路径。

综上，给定车场布置及能力、折返站布置及能力、以及运营时段初需要车底的列车，城市轨道交通线路运营时段前车底空驶出场路径问题可描述为：指派列车所需车底的配属车场和空驶出场路径(可为直达或折返路径)，以使得所有列车所需的车底得到满足，所有车场的检修及出车能力、以及所有折返站的折返能力不违背，且总空驶距离最小。

1.2 问题假设

具有多交路、多车场和多车型的城市轨道交通线路全日车底出入场运行线编制比较复杂，为获得理论最优的结果，理想的求解策略应将运营时段前车底集中出场、运营时段内车底分散出入场和运营时段后车底集中入场过程进行综合优化，但该策略对于复杂的城市轨道交通线路建模和求解难度较大。在假定运营时段内列车运行图和车底交路计划给定的前提下，本文着重探讨运营时段前车底集中空驶出场路径优化问题。为对所研究问题做出更为清楚的界定，特制定以下假设：

假设1 城市轨道交通线路普遍对车底采用“从哪儿出回哪儿去”的运用规则，由此，车底在运营时段内的分散出入场安排在一定程度上受其在运营时段前集中出场路径的影响，但与集中出场情况不同，分散出入场发生在运营时段内，一般允许载客且不会产生空驶距离，故暂不考虑运营时段内车底分散出入场路径及其对应运行线的编制。

假设2 车底在运营时段后的集中入场安排同时受其在运营时段前集中出场和在运营时段内分散出场路径的影响，在单独优化运营时段前集中出场路径时，难以直接对运营时段后集中入场路径进行综合优化；同时，运营时段后车底一旦担当完最后一列列车，只需在终到站直接顺向或经折返后逆向返回其配属车场，相比于运营时段前集中出场过程，空驶距离节约显著，故暂不考虑运营时段后车底集中入场路径及其对应运行线的编制。

假设3 假设在所研究的线路上各车场只与1个端点站或中间站接轨，注意，本文方法可容易地拓展来描述两站接轨、区间接轨等更复杂的车场与其所在站间的接轨方式。

假设4 车底在运营时段前集中出场时一般不允许沿途逗留，且需在线路运营开始时刻前运行至担当列车的始发站，由此出场路径是车底出场运行安排的关键决策，给定出场路径，车底在其路径上的可行出场运行线可采用简单规则确定，故暂不考虑运营时段前车底集中出场运行线的编制。为了在获得出场路径后可勾画出高质量的出场运行线，特别是控制车场和折返站的最早工作时刻，特约定车场在线路运营开始时刻前只有有限的时间可用于往两个方向发出车底，同时，折返站也只能在线路运营开始时刻前给定的可用时间内对车底进行折返。

2 数学模型

2.1 符号说明

为便于模型构建，对需要使用的符号进行定义和说明：

定义集合如下：S为城市轨道交通线路上的车站集合，沿上行方向从前往后编号，s∈S；D为车场集合，d∈D；K为折返站集合，k∈K；I为运营时段初需由车场的车底通过空驶出场进行担当的列车集合，i∈I，根据给定的车底交路计划确定；W为运行方向集合，W={0，1}，w=0表示上行方向，w=1表示下行方向；V为按编组辆数进行区分的车底类型集合，v∈V，按编组辆数由少到多编号；Id={i∈I|bodqi=ui}⊂I，表示可由车场d的车底采用直达出场路径进行担当的列车集合；Vd⊂V，表示车场d所能(日常)检修的车底类型集合；Di={d∈D|bodqi=ui}⊂D，表示发出的车底可对列车i采用直达出场路径进行担当的车场集合；Kid={(k∈K)|bodpk=1-ui,bpkqi=ui}⊂K，表示列车i所需车底从车场d始发并采用折返出场路径对应的折返站集合。

定义常数如下：lss′为车站s和s′之间的距离，等于其包含区间的距离之和；bss′为车底从车站s至s′的运行方向，根据定义，bss′等于0或1；od为车场d所在的车站；gdv为每日车场d可(日常)检修的类型为v的最大车底数量;adv为运营时段内需由车场d类型为v的车底担当的列车数量，由车底交路计划进行确定；edw为运营时段前车场d可向方向w发出的最大车底数量，可根据给定的可用出车时间和单向出车间隔进行估算；nd为运营时段前车场d可向两个运行方向总共发出的最大车底数量，可根据给定的可用出车时间和双向出车间隔进行估算；fdw为向方向w发出的车底从车场d至该车场所在站的走行距离；pk为折返站k对应的车站。rkw为运营时段前折返站k可将运行方向从1-w折返为w的最大车底数量，可根据给定的可用折返时间和单向折返间隔进行估算；hkw为在折返站k，车底的运行方向从1-w折返为w的走行距离；qi为列车i的始发站；ui为列车i的运行方向；ti为列车i所需车底的类型。

定义变量如下：xid为0-1变量，若列车i由车场d的车底采用直达路径进行担当，取为1，否则为0；yidk为0-1变量，若列车i由车场d的车底采用经折返站k的折返路径进行担当，取为1，否则为0；cid为连续变量，表示车底从车场d至所担当列车i始发站的空驶出场距离。

2.2 目标函数

车底在运营时段前集中出场沿途不允许载客，需快速运行至所担当列车的始发站。为降低运输成本，提高车底运用效率，应最小化车底出场总空驶距离，即

( 1 )

式中:cid为车底从车场d至担当列车i始发站的空驶出场距离，其取值依赖于车底的出场路径、车场的出车距离、折返站的折返距离以及站间距离，可采用下式进行计算

cid=(fdui+lodqi)·xid+

( 2 )

式中：当列车i所需车底从车场d始发并采用直达路径出场(即xid=1)时，空驶出场距离cid等于车场d在列车i运行方向上的出车距离fdui与车场d所在站至列车i始发站的距离lodqi之和。当列车i所需车底从车场d始发并采用经折返站k*的折返路径出场(即yidk*=1)时，空驶出场距离cid由4部分组成：车场d在列车i相反运行方向上的出车距离fd,1-ui、车场d所在站至折返站k*的距离lod,pk*、折返站k*在列车i运行方向上的折返距离hk*,ui、折返站k*至列车i始发站的距离lpk*,qi。

2.3 约束条件

车底空驶出场路径优化问题还需满足一系列运营和能力约束。

(1) 路径唯一性约束

为获得符合现场实际的运营时段前车底集中出场路径，任意列车所需的车底必须且只能选择一条始发于可检修其车底类型的车场的直达或折返路径出场即

∀i∈I

( 3 )

(2) 路径可行性约束

城市轨道交通线路通常只设置2条正线，上下行方向各占用1条，除折返站和车场所在站外，普通车站一般不设置配线，使得不是所有车场和所有列车间同时存在可行的直达和折返出场路径。给定列车i和车场d，根据列车i的运行方向、列车i始发站和车场d所在站的相对位置，有4种可行的车底出场路径，见图2。

如图2(a)所示，列车i为上行列车，若车场d所在站沿着上行方向在列车i始发站的后方，则列车i可由车场d的车底采用直达出场路径进行担当；反之，列车i与车场d间不存在可行的直达出场路径，即若d∉Di，必存在xid=0。

如图2(b)所示，列车i为下行列车，若车场d所在站在列车i始发站的后方，则列车i不能由车场d的车底采用直达出场路径进行担当，即若d∉Di，必存在xid=0。

如图2(c)所示，列车i为上行列车，若车场d所在站在列车i始发站的后方，且在车场d所在站的后方存在合适的折返站Kid，则列车i可由车场d的车底采用经Kid中任意站的折返出场路径进行担当，在图中以虚实线表示；反之，若车场d所在站在列车i始发站的前方，且在车场d所在站的后方可找到合适的折返站Kid，则列车i与车场d间同样存在经Kid中任意站的折返出场路径，如图中粗实线所示。换言之，对于列车i和车场d，若Kid=∅，可令yidk=0。

如图2(d)所示，列车i为下行列车，无论车场d所在站在列车i始发站的前方还是后方，只要在车场d所在站的前方不存在折返站Kid，则列车i不能由车场d的车底采用经Kid的折返出场路径进行担当，即若Kid=∅，可令yidk=0。

(3) 车场检修能力约束

城市轨道交通线路通常只配备1种车底，但可采用不同的编组辆数，基于此，本文将车底按编组辆数进行分类，典型的有4编车底、6编车底和8编车底等。为确保行车安全，车底具有严格的检修制度，包括列检、月检、定修、架修和厂修等修程，在每运营一定时间或里程后需开展相应修程的检修，其中，列检和月检等日常检修作业通常固定在配属车场进行。受场站特别是停车库和列检/月检库设计的限制，各车场对各类型的车底只有有限的日常检修能力，需要指出的是，短编车底可在检修长编车底的车场进行日常检修。因此，在确定运营时段前车底空驶出场路径时，需满足配属于各车场的各类型车底数(含该类型车底编组长度以下的短编车底数)不能超过该车场对该类型车底的最大日常检修能力。

同时，根据实际运营情况，除了检修车底和备用车底以外，车场停留的运用车底实际上由两部分构成，一部分为运营时段前集中出场以为运营时段初列车服务的车底，另一部分为运营时段内分散出场以为平高峰过渡期间高峰列车服务的车底。因此，在表达运营时段前车场的检修能力约束时，应扣除被运营时段内分散出场车底占用的能力，即

( 4 )

(4) 车场出车能力约束

城市轨道交通线路的车场与其所在站间通常设置有2条联络线，分别为出场线和入场线，运营时段前，2条联络线都作为出场线使用，但两出车方向往往各自占用1条。同时，受车场信联闭设备的限制，为确保车底运行安全，不仅两相邻同方向车底间需满足必要的出车间隔，两相邻反方向车底间也需满足安全的出车间隔。另一方面，现场规定车场只能在最早工作时刻之后出车，且车底必须在线路运营开始时刻之前到达所担当列车的始发站，使得车场在运营时段前的可用出车时间是有限的。因此，运营时段前，受出车时间和出车间隔的限制，各车场在各运行方向上只有有限的出车能力为

∀d∈Dw∈W

( 5 )

同时，各车场在两个运行方向上的总出车能力也是有限的为

∀d∈D

( 6 )

(5) 折返站能力约束

为便于日常运营组织和调度指挥，城市轨道交通线路通常在其端点和沿线设置若干折返站，利用站前或站后渡线将车底从一个运行方向折返为另一个运行方向。在实际情况中，大多数折返站只具备1个方向的折返能力，只有少部分折返站可同时折返两个方向的车底。由于车底在折返站转向需走行一段距离，且对折返站接发车作业造成较大干扰，为确保折返站作业安全，在现有的信联闭条件下，两相邻折返车底间需满足安全的时间间隔。同时，折返站在开始工作至线路开始运营之间只有有限的折返时间可用。因此，运营时段前，在各折返站各运行方向上折返的车底数不能大于该站在该方向上的最大能力，即

∀k∈Kw∈W

( 7 )

(6) 变量取值约束

xid={0,1} ∀i∈Id∈Di

( 8 )

yidk={0,1} ∀i∈Id∈Dk∈Kid

( 9 )

2.4 整体模型

综上，城市轨道交通线路运营时段前车底空驶出场路径问题可构建为

(M)式( 1 )

s.t. 式( 2 )～式( 9 )

车底空驶出场路径问题可约简为具有顶点能力约束的整数多商品网络流问题，后者已被证明为NP-hard问题[15]，因此，原问题本质上是NP-hard的。由既有算法理论可知，对于NP-hard问题，一般难以开发精确算法，可在多项式时间内找到最优解，甚至是可行解。然而，所构建模型(M)为混合整数线性规划模型，还可进一步表达为纯0-1线性规划模型，该模型最坏情况下包含|D|×|K|×|I|个变量和|I|+|D|×|V|+|D|×|W|+|D|+|K|×|W|个约束，模型规模随车场、折返站和列车的数量呈多项式增长。初步计算测试结果表明，基于该模型，当前诸多主流商业优化软件(例如CPLEX、GUROBI)只需在普通计算机上便可将大规模切实算例快速求解到最优。因此，借助于线性模型(M)，本文直接采用商业优化软件求解所提出的车底空驶出场路径优化问题。

3 算例分析

3.1 算例描述

以某城市轨道交通线网中最繁忙线路为背景，如图3所示，对所提出方法进行验证。测试线路全长54 km，设车站39座，平均站间距1 421.1 m，2015年日均客流量达69.8万乘次，全年客流量超2.5亿乘次。线路配备六编和八编两种车底，运营3条列车交路，第1条交路的端点为车站s1和s26，第2条交路的为车站s12和s32，第3条交路的为车站s12和s39。线路6:30开始运营，22:30结束运营。全线在中部和接近端点处分别设置大型车场d1和小型车场d2，车场d1可同时检修六编和八编车底，车场d2只可检修六编车底，两车场在运营时段前的可用出车时间为60 min，两个运行方向的出车间隔和距离相同，车场其他基本信息见表1。全线在沿线较为均匀地设置折返站10个，其中，上行折返站6个，下行折返站4个，目前在日常运营组织中只启用折返站6个，剩下4个备用，所有折返站只能往1个运行方向对车底进行折返，且运营时段前的可用折返时间为60 min，折返站其他基本信息见表2。

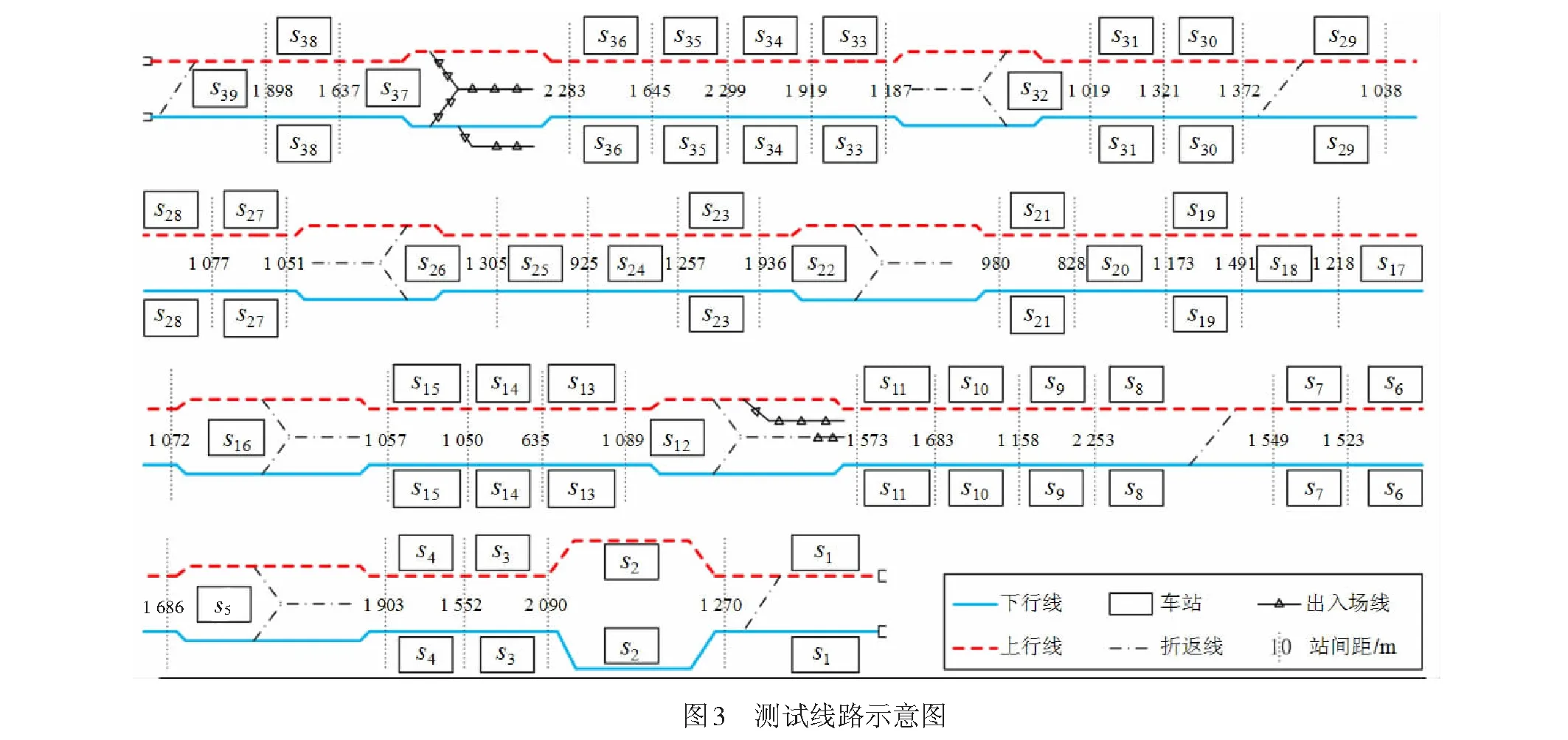
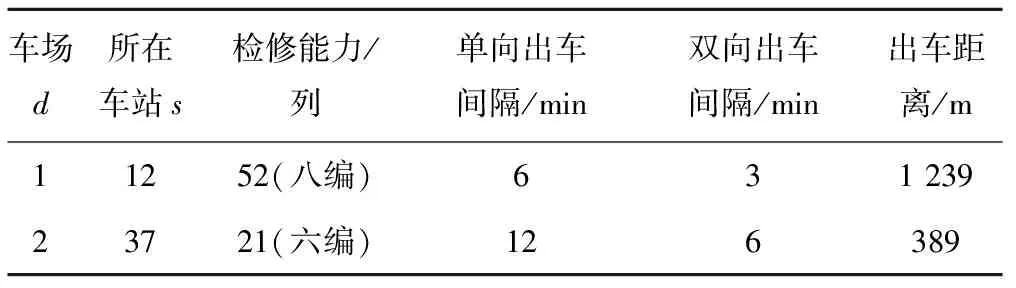
表1 车场基本信息

选择测试线路2015年工作日的分号列车运行图进行算例分析。在编制完测试运行图的车底交路计划后，测试线路运营时段初共有29列列车需由车场d1和d2始发的车底进行担当，其基本信息见表3。其中，第1～3列表示列车的信息，第4～7列表示由计划编制人员凭借经验确定的列车所需车底的空驶出场路径相关信息，后7列含义与前7列相同。同时，测试线路在运营时段内需要车场d1发出6列六编车底和9列八编车底、车场d2发出8列六编车底，意味着运营时段前车场d1和d2的实际检修能力分别为37列八编车底和13列六编车底。

表2 折返站基本信息

注：折返站k4对应的车站s12同时为车场d1所在的车站，运营时段前只供车底出场，不供车底折返。

表3 列车基本信息

注：列车16和20需要八编车底进行担当，其余列车需要六编车底进行担当。

3.2 计算结果

采用IBM ILOG CPLEX OPL编程所提出的优化方法，并调用CPLEX 12.5.1求解所构建的优化模型(M)。将CPLEX的相关参数取为默认值，并基于其内嵌的集成分支定界和割平面算法的分支切割算法将模型(M)求解到最优。所有计算在CPU为Inter Core i7-4700MQ 2.40 GHz，内存为8 GB，操作系统为Windows 10-64位的普通计算机上运行。

对测试算例，运用上述优化方法，耗时不到1 s，获得车底空驶出场路径见表4，其中，距离缩短率为优化结果相比于经验方法的空驶出场距离缩短率，增加为正值，缩短为负值。从表4可看出，受车场位置和能力的影响，21列列车(含全部的13列上行列车和8列下行列车)的车底从位于线路中部的大型车场d1始发，只有剩下8列下行列车的车底从靠近线路端部的小型车场d2始发。同时，为最小化车底总空驶距离，只有11列列车(包括6列上行列车和5列下行列车)的车底选择折返路径出场，剩下18列列车的车底选择直达路径出场。

将表3与表4进行对比可发现，与现场计划编制人员的经验方法相比，所提出的优化方法未显著改变列车所需车底的空驶出场路径，只有2列列车所需车底的出场路径从原来的直达路径调整为折返路径，空驶距离有所延长，但与此同时，4列列车所需车底的出场路径从原来的折返路径调整为直达路径，空驶距离大为缩短。最终，优化方法经过简单的调整将总空驶距离从原来的473.388 km减小为444.697 km，总空驶距离缩短28.691 km，占原总空驶距离的6.1%，年总空驶距离预计可缩短超1万km。因此，优化方法既具有较好的求解效果，又具有非常快的求解速度，完全可用于提高运营时段前车底空驶出场路径的质量。

基于表4还可统计车场和折返站的能力占用情况，该信息有助于识别能力瓶颈，从而为进一步缩短车底总空驶距离提供有效提示。车场的能力占用情况见表5，其中，第6列、第7列分别为上行和下行发出的车底数，第8列～第11列分别为车场检修能力的占用率、上行、下行和双向出车能力的占用率。从表5可见，两车场的检修能力占用率低于65%，反映该算例中车场的检修能力对车底的空驶出场路径无实质性影响。然而，车场1的下行和双向出车能力全部占用，车场2的下行出车能力也全部占用，意味着车场的出车能力显著影响车底的空驶出场路径。折返站的能力占用情况见表6，其中第1列为折返站编号。由表6可得，只有3个折返站存在列车折返，且其折返能力占用率低于50%，说明折返站的能力不影响车底的空驶出场路径。

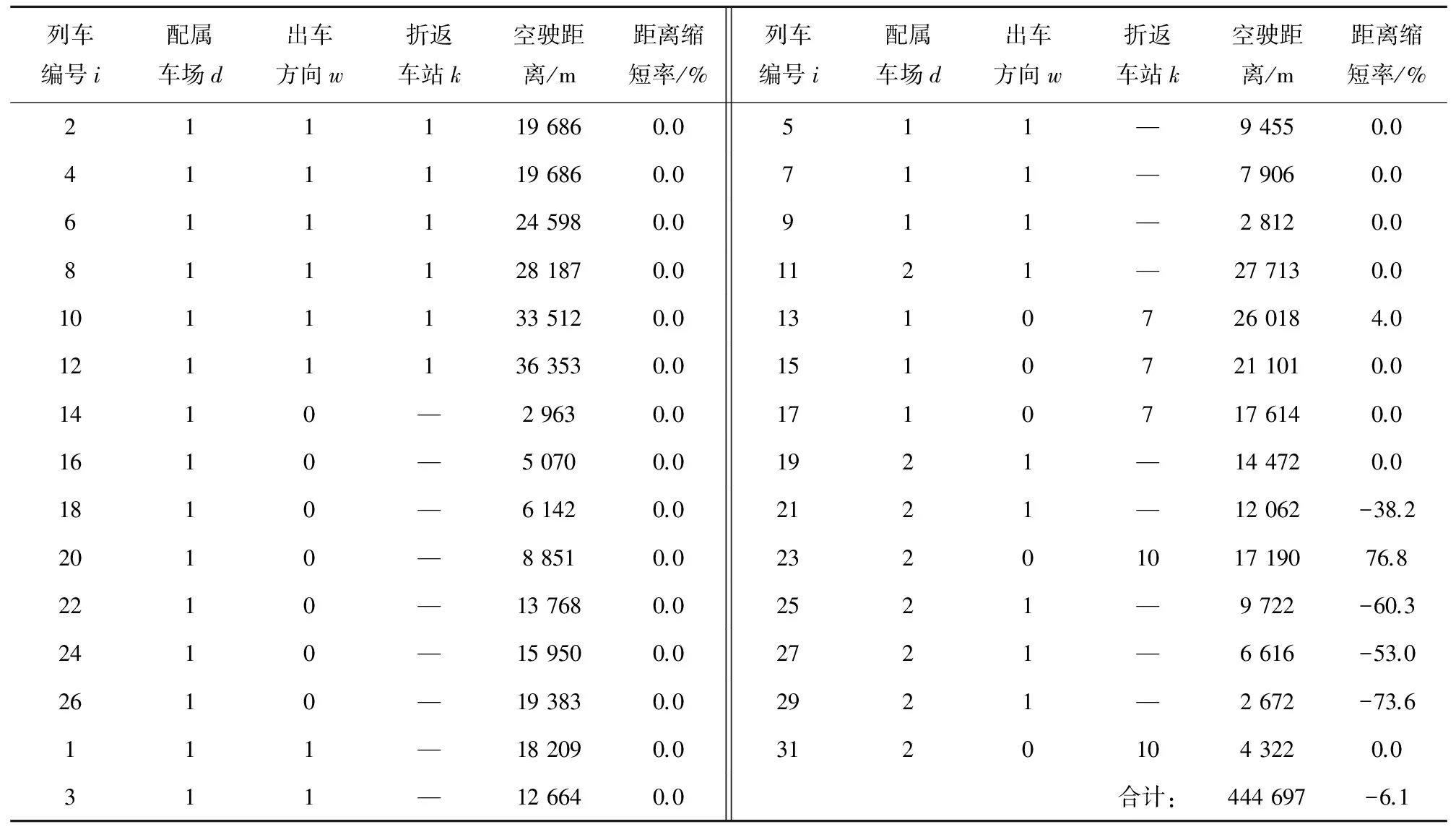
表4 基于优化方法的车底空驶出场路径

表5 车场能力占用

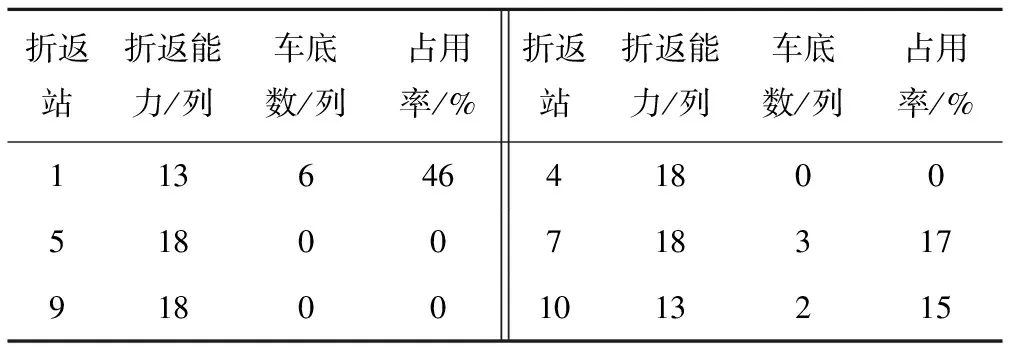
表6 折返站能力占用

3.3 缩短总空驶距离的措施

本节采用灵敏度分析方法探求可进一步缩短车底总空驶距离的有效措施。根据测试算例的现状及其车场和折返站在优化后的能力占用情况，考虑2个有望缩短车底总空驶距离的措施，一个为开放未启用的折返站，另一个为延长车场的可用出车时间。

(1) 开放未启用的折返站

首先评估开放未启用的折返站对车底总空驶距离的影响。如3.1节所述，测试线路共设置10个折返站，有6个折返站{1，4，5，7，9，10}已启用，还有4个折返站{2，3，6，8}未启用。对于未启用的折返站，设计16种折返站开放方案，灵敏度分析结果如图4所示。其中，横轴表示折返站的开放方案，最左边方案为基本方案，只包含已启用的6个折返站，后续方案为待评估的方案，其括号内数字表示在基本方案的基础上新开放的折返站。左纵轴表示各方案对应的总空驶距离，以柱形图表示，最上方的水平虚线表示经验方法对应的总空驶距离。右纵轴表示各方案相比于经验方法的总空驶距离缩短率，以折线图表示。

从图4可看出，若考虑只新开放1个折返站，开放折返站2或3均可明显缩短车底的总空驶距离，且开放折返站3的效果更好。若考虑新开放2个折返站，开放折返站2或3的方案优于其他方案，同时开放折返站2和3的方案效果最好。若考虑新开放3个折返站，同时开放折返站2和3的方案比其他方案更优。总的来看，同时开放折返站2和3的四个方案为最优方案，车底总空驶距离为385.082 km，与经验方法相比，总空驶距离缩短88.306 km，缩短率达18.7%。鉴于折返站2和3比较接近，建议新开放折返站3，此时，车底总空驶距离为 398.585 km，相对于经验方法，总空驶距离缩短74.803 km，缩短率为15.8%，只比最优方案少2.9%。综上，开放未启用的折返站是缩短车底总空驶距离的有效措施，但是，该措施将增加设备维护和人力资源等费用，在实际应用时需通过技术经济比较加以确定。

(2) 延长车场的可用出车时间

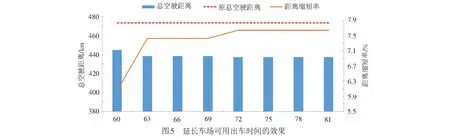
其次评估延长车场的可用出车时间对车底总空驶距离的影响。3.2节已指出，车场的出车能力非常紧张，制约着车底出场路径的优化，对此，可尝试提高车场的出车能力，以进一步缩短车底的总空驶距离。车场的出车能力等于出车时间除以出车间隔，因此，为提高车场的出车能力，既可延长出车时间，也可缩短出车间隔。此处考虑前项措施，将车场的出车时间从当前的60 min逐步延长至 81 min，步长为3 min，设计8种出车时间方案，灵敏度分析结果如图5所示。其中，横轴为出车时间方案，各方案的数字表示其对应的出车时间。左纵轴为各方案对应的总空驶距离，以柱形图表示，同样在最上方以水平虚线标记经验方法对应的总空驶距离。右纵轴为各方案相对于经验方法的总空驶距离缩短率，以折线图表示。

图5显示，当车场出车时间从当前的60 min延长至72 min时，车底总空驶距离有所缩短，但当车场出车时间继续延长时，车底总空驶距离保持不变。在其他条件保持现状的前提下，将车场出车时间延长12 min，可获得最优的车底出场路径，总空驶距离为437.229 km，相比于经验方法缩短36.159 km，缩短率为7.6%。利用表5的车场能力占用统计情况可对图5中的变化规律进行解释。当出车时间取为72 min时，车场1的双向出车能力为25列，小于其实际检修能力，同时，车场2的双向出车能力为13列，正好等于其实际检修能力。因此，当出车时间小于72 min时，两车场的出车能力为瓶颈，此时延长出车时间有利于缩短车底总空驶距离。然而，当出车时间大于72 min时，车场2的检修能力将成为瓶颈，此时继续延长出车时间不能改进车底运用效率。综上，当车场出车能力紧张而检修能力富余时，延长车场出车时间有机会进一步缩短车底总空驶距离，然而，当车场出车能力比检修能力富余时，需同时提升车场的出车和检修能力才可能取得好的。

4 结论

运营时段前车底集中空驶出场路径优化是城市轨道交通线路全日车底出入场运行线以及车底运用计划编制的重要决策，但目前该问题并未获得企业界和学术界的广泛关注，且在现场主要由工作人员凭借经验编制，解的质量难以得到保证。在分析城市轨道交通线路运营时段前车底集中出场过程的基础上，以总空驶距离最小为目标，考虑诸多的实际运营和能力约束，为具有多交路、多车场和多车型的车底空驶出场路径问题，构建混合整数线性规划模型，该模型的规模对于车场、折返站和列车的数量多项式有界。计算结果表明，所提出的模型可帮助主流商业优化软件在普通计算机上将大规模问题快速求解到最优，所提出的优化方法在解的质量上优于现场采用的经验方法。另外，若技术经济条件允许，可通过开放未启用的折返站或延长车场的可用出车时间，以进一步缩短车底集中出场的总空驶距离。

作为全日车底出入场运行线编制的重要决策之一，本文问题具有研究难度和改进空间，可在以下几个方面作进一步拓展。首先，可将所提出的模型应用于解决更多或更复杂的实际问题，以评估该模型对实际问题的求解能力，并分析继续开发更有效求解算法的必要性。其次，实际情况中，城市轨道交通线路的车底在运营时段前需按运行线而不只是路径集中空驶出场，未来有必要将所提出的出场路径方法拓展来解决出场运行线编制问题。另外，城市轨道交通线路的车底在运营时段前集中出场、运营时段内分散出入场以及运营时段后集中入场，如何在已存在大量列车运行线的运行图空隙中插入全日车底出入场运行线(即综合解决全日车底出入场运行线编制问题)也是下一步值得开展的工作。

参考文献：

[1] NIU H, ZHOU X. Optimizing Urban Rail Timetable under Time-dependent Demand and Oversaturated Conditions[J]. Transportation Research Part C：Emerging Technologies, 2013, 36(11):212-230.

[2] NIU H, ZHOU X, GAO R. Train Scheduling for Minimizing Passenger Waiting Time with Time-dependent Demand and Skip-stop Patterns:Nonlinear Integer Programming Models with Linear Constraints[J]. Transportation Research Part B：Methodological, 2015, 76:117-135.

[3] SUN L, JIN J G, LEE D H, et al. Demand-driven Timetable Design for Metro Services[J]. Transportation Research Part C：Emerging Technologies, 2014, 46:284-299.

[4] BARRENA E, CANCA D, COELHO L C, et al. Exact Formulationsand Algorithm for the Train Timetabling Problem with Dynamic Demand[J]. Computers & Operations Research, 2014, 44(3):66-74.

[5] BARRENA E, CANCA D, COELHO L C, et al. Single-Line Rail Rapid Transit Timetablingunder Dynamic Passenger Demand[J]. Transportation Research Part B：Methodological, 2014, 70(C):134-150.

[6] 许红,马建军,龙建成,等. 城市轨道交通列车运行图编制的数学模型及方法[J]. 北京交通大学学报, 2006, 30(3):10-14.

XU Hong, MA Jianjun, LONG Jiancheng, et al. Study on Model and Method of Train Working Diagram of Urban Rail Transit[J]. Journal of Beijing Jiaotong University, 2006, 30(3):10-14.

[7] 江志彬,徐瑞华,吴强,等. 计算机编制城市轨道交通共线交路列车运行图[J]. 同济大学学报(自然科学版), 2010, 38(5):692-696.

JIANG Zhibin, XU Ruihua, WU Qiang, et al. Shared-path Routing Timetable Computer Designing in Rail Transit System[J]. Journal of Tongji University (Natural Science), 2010, 38(5):692-696.

[8] 王媛媛. 城市轨道交通列车运行图编制理论与方法研究[D]. 成都:西南交通大学, 2013.

[9] CADARSO L, MARIN A. Robust Rolling Stock in Rapid Transit Networks[J]. Computers & Operations Research, 2011, 38(8):1131-1142.

[10] CADARSO L, MARIN A. Robust Routing of Rapid Transit Rolling Stock[J]. Public Transport, 2010, 2(1):51-68.

[11] CADARSO L, MARIN A. Improving Robustness of Rolling Stock Circulations in Rapid Transit Networks[J]. Computers & Operations Research, 2014, 51(3):146-159.

[12] 江志彬,徐瑞华,吴强,等. 多交路共线运行的城市轨道交通车辆运用优化[J]. 同济大学学报(自然科学版), 2014, 42(9):1333-1339.

JIANG Zhibin, XU Ruihua, WU Qiang, et al. Optimal Model for Using of Transit Unit Based on Shared-path Rail Transit Route[J]. Journal of Tongji University (Natural Science), 2014, 42(9):1333-1339.

[13] 何必胜,宋瑞,何世伟,等. 城市轨道交通车底运用计划编制优化模型求解的混合列生成算法[J]. 中国铁道科学, 2014, 35(1):122-129.

HE Bisheng, SONG Rui, HE Shiwei,et al. A Hybrid Column Generation Approach for Solving Rolling Stock Assignment Optimization Model of Urban Rail Transit[J]. China Railway Science, 2014, 35(1):122-129.

[14] 郑锂,宋瑞,肖赟,等. 网络化运营下城市轨道交通列车车底运用计划编制的优化方法[J]. 中国铁道科学, 2014, 35(2):104-110.

ZHENG Li, SONG Rui, XIAO Yun, et al. Optimization Method for Working Out Vehicle Scheduling Plan of Urban Rail Transit under Network Operation[J]. China Railway Science, 2014, 35(2):104-110.

[15] EVEN S, ITAI A, SHAMIR A. On the Complexity of Time Table and Multi-commodity Flow Problems[C]//16th Annual Symposium on Foundations of Computer Science. New York:IEEE,1975:184-193.