航空地面电源车备件供应能力建模仿真研究∗

许浩杰 李 康 黄之杰

（空军勤务学院航空四站系 徐州 221000）

1 引言

备件对航空地面电源车的维修保障工作至关重要，能否及时有效地提供备件供应，直接影响装备的维修工作以及任务的完成情况。航空地面电源车是飞机飞行训练的重要地面保障装备，现阶段其备件的配置工作主要依靠历史消耗记录或经验数据进行，较少考虑航空地面电源车在不同部署站点的任务强度和使用过程中的动态因素，缺乏有效手段衡量备件库存与备件需求之间的动态关系，致使部分易故障单元数量配置不足或无备件库存，严重制约航空地面电源车的备件供应效率和保障能力。为此，本文立足于航空地面电源车的实际使用情况，综合考虑任务、预防性维修和修复性维修等因素，以备件延期交货量和备件短缺风险为评价指标，建立仿真模型对航空地面电源车的备件供应能力进行研究，统计计算各指标随任务时间的变化情况，为航空地面电源车的备件供应能力评判和备件配置提供决策依据。

2 备件供应能力评价指标

备件在装备的保障资源中占有极其重要的地位，航空地面电源车的备件供应能力受诸多因素影响，如备件库存量、备件供应时间、站点备件配置比例和备件周转时间等［1］。其中，备件延期交货量和备件短缺风险不仅能够较好地衡量既定条件下库存满足需求的能力，还能反应保障系统的综合保障能力［2］，因此选取备件延期交货量和备件短缺风险作为航空地面电源车备件供应能力的评价指标。

备件延期交货量（Number of Backorder，NBO）指保障站点备件库存与需求量之差的平均值，用于描述库存对备件需求的满足程度［2］。航空地面电源车的备件延期交货量在服役期内是随机变化的，即其备件延期交货量的变化是一个随机动态过程。

备件短缺风险（Risk of Shortage，ROS）表示特定条件下备件库存无法满足需求的概率。是检验备件库存对需求满足程度的重要指标［3］。与备件延期交货量不同的是，备件短缺风险与等待时间无关，在备件短缺风险数值很低的情况下，如果等待时间非常短，保障系统的保障能力仍可能处于较高水平。

3 备件需求模型

航空地面电源车由多个子系统组成，各子系统又可分为众多可修单元和不可修单元。无论是可修单元还是不可修单元，在任务执行过程时都有可能发生随机性故障，故障的排除需要通过修复性维修作业来完成，这一过程就会产生备件需求。另外，在不可修单元进入耗损期之前，需要通过定期维护的方式预防故障的发生，即在单元的预防性维修作业中需要根据检查结果进行备件更换作业，这一过程也会有备件需求产生。下面从修复性维修和预防性维修两方面建立备件需求模型。

3.1 修复性维修备件需求模型

修复性维修是航空地面电源车主要的备件需求来源。若在时间间隔T内，对航空地面电源车进行修复性维修作业的备件需求数量为XN(T)，该段时间内备件需求数量为K的概率记为p(K，T)，假设单元故障前能工作时间服从指数分布，则时间间隔T内备件需求数量服从泊松分布［4］，即

式中λ表示修复性维修作业的备件需求率，与单元的平均故障间隔时间TMBF和修复性维修作业消耗的备件数量N有关，可用下式表示：

对航空地面电源车在时间间隔T内的备件需求分布函数进行抽样，即在区间（0，1）内抽取均匀随机变量，则修复性维修的备件需求数量可表示为［4］

3.2 预防性维修备件需求模型

航空地面电源车预防性维修作业中需要更换的单元一般为有寿单元，且大多数有寿单元为不可修件［5］。预防性维修通常根据装备的日历时间进行［6］，假设在TG时刻，某类单元预防性维修作业的备件数量需求为NPM(TG)，如果航空地面电源车某类组成单元在TG时刻的可靠度为R(TG)，故障率为λP，且该类单元的使用寿命服从指数分布，则其可靠度为

假设有m个该类单元需要更换，则对于l个进行预防性维修的该类产品而言，在TG时刻进行预防性维修作业备件需求量为m的概率服从二项分布［7］，即，且令

对预防性维修作业的备件需求分布函数进行抽样，即在区间（0，1）内抽取均匀随机变量

由此，航空地面电源车某类组成单元在TG时刻进行预防性维修作业的备件需求数量可表示为

4 备件库存及周转模型

不同于水面舰艇、飞机和坦克等主战武器的三级保障体制［8～10］，航空地面电源车的保障组织无严格意义上的基层级、中继级和基地级划分，其维修保障组织主要包括四站连、航材股和修理厂三类（以下分别称作站点1、站点2和站点3）。站点1（四站连）是航空地面电源车的部署使用单位，具有一定的维修能力且拥有部分备件库存。站点2（航材股）不具备装备修理能力，但具有一定的备件库存且是备件周转的媒介。站点3（修理厂）是航空地面电源车的生产单位，既具有完全修理能力，也拥有绝对数量的备件库存，是航空地面电源车保障组织中的终极站点。

若航空地面电源车在执行保障任务过程中发生故障，或在进行预防性维修时发现部分组成单元可靠度无法满足继续使用条件时，均会出现备件需求。图1以现场可更换单元LRU和车间可更换单元SRU为例，对出现备件需求时的备件周转过程进行了描述。备件需求首先从站点1（记为一级）开始进行匹配，故障LRU通过更换进行修复，被更换的LRU如果可修复，则根据各级站点的维修能力进行维修匹配，否则进行报废处理。若站点1无所需备件库存，则向站点2（记为二级）提出备件申请，若站点2现有库存满足要求，则向站点1进行备件周转，反之，向站点3（记为三级）继续进行备件申请。站点1的备件消耗通过站点2和站点3进行补充，站点2的备件消耗通过站点3进行补充，站点3的备件消耗通过向供货商再订购进行补充。模型中假设保障站点的实际备件库存等于初始库存，所重点研究的是实际备件库存低于初始库存的情况。另外，备件的周转模型不考虑同等级站点的横向保障情况（例如相邻地点航材股之间的备件调拨）。

图1 备件库存及周转模型

5 评价指标计算模型

5.1 备件延期交货量计算模型

根据备件延期交货量的定义，若航空地面电源车共由NZ个基本单元组成，备件库存站点数量为n，第i个单元在第j个站点的备件需求量为第i个单元在第j个站点的备件库存量为则在第j个站点，航空地面电源车备件需求量与库存量的差值之和的绝对值Nj可表示为

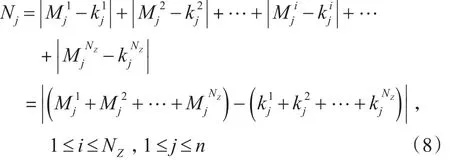
由此，航空地面电源车的备件延期交货量可表示为

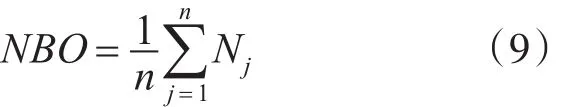
5.2 备件短缺风险计算模型

备件短缺风险和备件保障率（P）是相对而言的，对于相同条件下同一库存站点而言，其备件短缺风险和备件保障率有如下关系［11］：

因此，可以从备件保障率的角度定量描述航空地面电源车的备件短缺风险。备件保障率通常用备件库存站点的服务水平进行描述，即

从单个组成单元的角度来看，备件保障率可用航空地面电源车各组成单元备件保障率的代数期望值表示。如果航空地面电源车由N个基本单元组成，在时间间隔T内，第i个单元需要进行Ni次更换作业，其实际库存数量为

由此，航空地面电源车总的备件保障率可表示为［3］，则第i个单元的备件保障率可表示为

若第i个单元在时间间隔T内出现故障的概率为，则总的备件保障率为

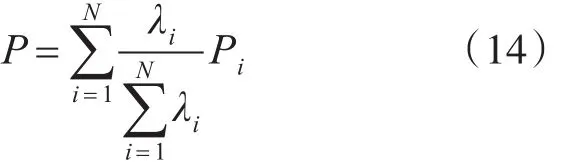
对于航空地面电源车而言，无论修复性维修还是预防性维修，所更换的单元均可分为可修复单元和不可修复单元两类。对于不可修复单元，在备件周转模型中做报废处理，对于可修单元，被更换后将在各级站点间进行维修匹配，被修复后进入站点继续周转。对于可能修复可能无法修复的单元，仿真时认为其为不可修单元。为更加贴近航空地面电源车的实际备件使用情况，以下分别建立可修单元和不可修单元的备件短缺风险计算模型。

5.2.1 可修单元备件短缺风险模型

由于可修单元在站点被修复后将继续进入周转过程，因此与不可修单元相比，同等条件下可修单元的备件需求量会有所减少。如图2所示，考虑可修单元的可修复性，认为其备件模型是多服务台的排队系统。在维修作业相互独立且平均服务率一致的条件下，假设可修单元的故障和修复时间均满足指数分布，若单元故障后有可用备件，则用备件更换故障单元，若无可用备件，则对可修故障件进行修复作业，维修期间装备处于不可工作状态，直至故障单元修复后以备件的形式重新使用［12］。由此，可修单元备件保障率转化为限定资源条件下可用单元大于等于L的概率问题。

图2 可修单元备件模型

若航空地面电源车中第i种可修单元数量为Li，备件库存数量为Di，故障率为φi，可维修站点数量为c，平均服务率为ρ，初始状态概率为P0，则根据排队论方法可知，在时间间隔内，航空地面电源车第i种可修单元需要μi个备件的概率为

对于初始状态概率P0，由于，所以：

另外，在备件库存数量为Di的情况下，航空地面电源车第i种可修单元的备件保障率与备件需求不大于Di的概率是等价的，从这个层面上讲，当航空地面电源车由于修复性维修或预防性维修而出现备件需求时，第i种可修单元的备件保障率为

根据式（15）可得

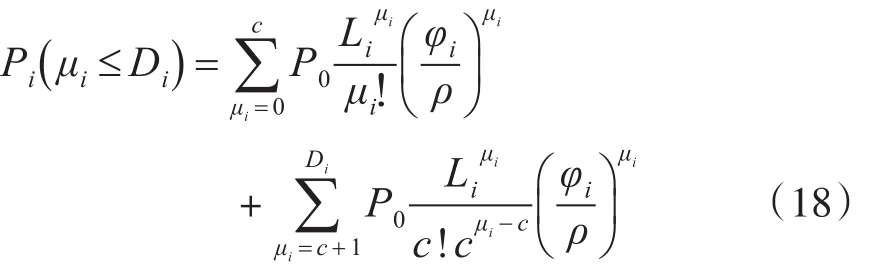
综上可知，航空地面电源车的备件保障率为

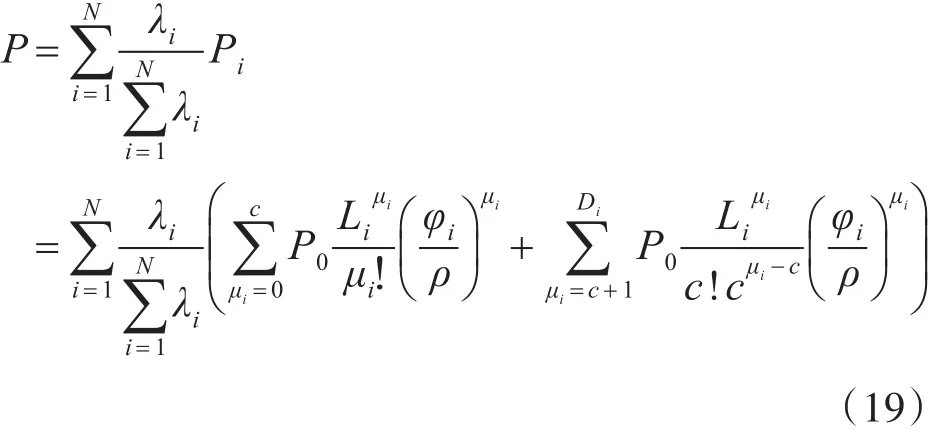
由此可计算航空地面电源车备件短缺风险：ROS=1-P。

5.2.2 不可修单元备件短缺风险模型

根据实际使用情况，假设航空地面电源车不可修单元的使用寿命服从指数分布，单位时间内不可修备单元需求数量服从泊松分布，参数记为λT。在时间间隔T内，若第i种不可修单元的备件库存量为Ui，其备件需求量为ηi的概率为［13］

根据可修单元备件保障率的分析，第i种不可修单元的备件保障率可表示为

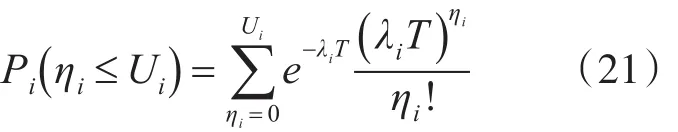
由此，根据式（14）和式（20）可得，航空地面电源车的备件保障率为

同样，由此可计算航空地面电源车备件短缺风险：ROS=1-P。

6 模型仿真原理

航空地面电源车是由多系统多部件组成的复杂装备，为提高模型的可操作性并简化问题的讨论，作如下基本假设：

1）航空地面电源车任一组成单元发生故障均会导致装备不可用，各组成单元之间的故障相互独立且不会在同一时刻发生；

2）模型中的单元只有“正常”和“故障”两种状态，更换备件后不影响装备的正常使用；

3）各站点储备的备件在仿真周期内不存在失效问题，即备件均是可用的；

4）组成单元的使用寿命、故障前能工作时间以及修复时间服从指数分布；

5）各站点备件初始库存水平已知；

6）备件周转过程仅考虑纵向层次，不考虑同等级站点间的横向保障问题。

航空地面电源车备件供应能力仿真评价以蒙特卡罗法和排队论为基础，通过任务的驱动作用模拟保障过程中的各类事件（执行任务、修复性维修、预防性维修和备件周转等），根据仿真中的备件需求与库存情况的对比，统计输出备件供应情况，仿真模型如图3所示。

图3 模型仿真原理图

7 实例分析

为检验仿真模型的可行性，以M型航空地面电源车为例，对其备件供应能力进行仿真研究。由于篇幅有限，输入数据仅列举部分单元。

7.1 仿真参数设定

1）仿真次数：50次；

2）仿真周期：8760h；

3）结果收集间隔期：48h；

4）初始随机种子数：123456789；

5）备件方案标识：方案1。

7.2 基本数据输入

表1 任务信息表

表2 保障组织信息表

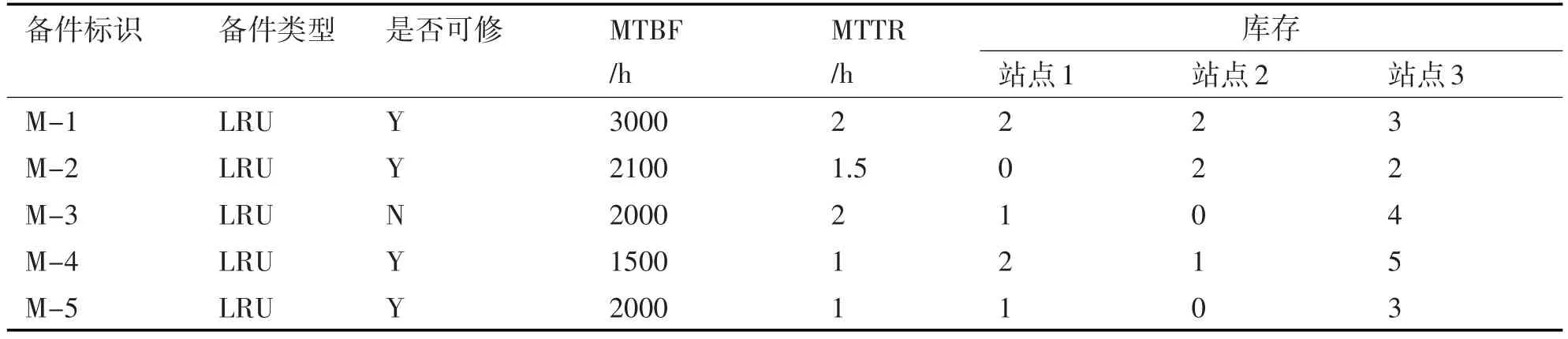
表3 初始备件库存信息表

7.3 仿真结果输出

仿真结果如图4和图5所示。图4为M型地面电源车备件延期交货量随时间变化图，图5是M型地面电源车备件短缺风险随时间变化图。

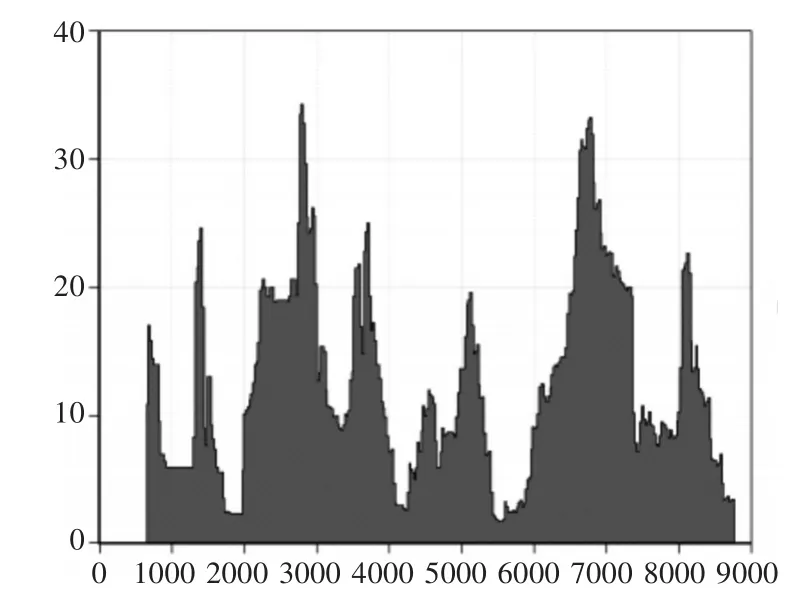
图4 备件延期交货量随时间变化仿真

对图4和图5的仿真结果求平均值，可得M型电源车仿真周期内备件延期交货量均值为11.6259，备件短缺风险为0.2422。在方案1的基础上，将站点1和站点2的备件库存数量增加2，其他条件不变，调整后的仿真结果如图6和图7所示。

图5 备件短缺风险随时间变化仿真

图6 调整后延期交货量随时间变化仿真

图7 调整后短缺风险随时间变化仿真

计算可得调整后的备件延期交货量均值为7.3041，备件短缺风险为0.1017。通过两次仿真结果的对比可以看出，增加站点1和站点2的备件库存数量可以明显提高M型航空地面电源车的备件供应能力，从而提高装备的使用可用度和任务成功率。这与实际的调研结果是相符的，M型航空地面电源车列装部队后，除装备自身性能外，影响装备保障使用的主要因素就是部署站点的备件短缺以及站点间周转耗时，仿真结果证明了模型的适用性和可行性。

8 结语

本文从航空地面电源车实际使用情况出发，以备件延期交货量和备件短缺风险作为评价参数，建立了包含备件需求模型、备件库存及周转模型和指标计算模型在内的仿真模型，并对仿真的基本原理进行了简要叙述。最后以M型航空地面电源车为例对模型进行了检验，仿真结果表明该模型合理可信，能够反映航空地面电源车的备件供应能力并为备件方案制定与配置工作提供决策参考。文中在建立仿真模型过程中作了一些基本假设，如组成单元使用寿命均服从指数分布和不考虑横向保障等，而在实际中不同组成单元的使用寿命可能服从不从分布，且横向保障也是存在的。另外，由于航空地面电源车部署站点众多，不可能在所有站点都等量配置备件，需要在有限备件资源条件下找出关键备件，有针对性地进行站点配置。因此，下一步需要对以上问题进行深入研究，使模型更具实际指导意义。

［1］王秀华，王建荣.装备可修复备件三级库存优化配置模型研究［J］.军事运筹与系统工程，2016，30（1）：59-64.

［2］徐廷学，魏勇，余仁波.面向任务的备件库存供应能力建模与仿真［J］.系统仿真学报，2012，24（4）：922-928.

［3］徐廷学，魏勇，顾钧元，等.基于库存方案的舰炮备件短缺风险建模与仿真［J］.舰船科学技术，2010，32（6）：121-127.

［4］郭霖瀚，王恺，王严，等.多级多层备件供应链需求建模与仿真［J］.计算机集成制造系统，2010，16（10）：2038-2043.

［5］张光宇，李庆民，郭漩.基于横向转运策略的可修备件多点库存建模方法［J］.系统工程与电子技术，2012，34（7）：1424-1429.

［6］靳登攀.关于两类备件保障指标的研究［J］.水雷战与舰船防护，2017，25（1）：20-24.

［7］李华，周亮，李庆民，等.有限维修力下作战单元装备可用度能评估及备件配置优化［J］.海军工程大学学报，2017，29（1）：69-73.

［8］王星.基于可修备件库存的设备运维系统仿真研究［D］.郑州：郑州大学，2017.

［9］徐立，李庆民，胡毅钧，等.有限维修能力下多级保障系统装备时变可用度评估及保障方案优化［J］.国防科技大学学报，2017，13（1）：23-27.

［10］王鸿东，易宏，梁晓锋，等.舰船备件配置研究现状与思考［J］.中国舰船研究，2016，23（4）：123-126.

［11］徐立，李庆民，李华，等.有限维修能力下作战单元时变可用度评估模型［J］.2016，17（1）：67-72.

［12］俞行.可维修备件多级保障库存优化研究及应用［D］.武汉：华中科技大学，2015.

［13］宋扬.复杂装备可维修备件供应保障策略仿真优化研究［D］.北京：北京科技大学，2015.