基于扩展卡尔曼滤波的雷测数据实时剔野方法∗

杨利斌 赵建军 季勤超

（海军航空大学 烟台 264001）

1 引言

常规数据处理理论是对观测数据进行事后处理，用参数估计方法对雷达测量数据进行分析。但在跟踪系统中，野值处理是属于动态测量数据中剔除野值的问题，因此必须对目标状态进行估计来获取观测误差，状态估计精度越高，则野值的判别效率越高［5］。卡尔曼滤波（KF）［6］适用于线性系统，但雷达跟踪目标时，通常雷达观测数据与目标参数间的关系是非线性的。对于非线性系统，常用的滤波方法有扩展卡尔曼滤波（EKF）［7～8］，不敏卡尔曼滤波（UKF）［9］和粒子滤波（PF）［10～11］。EKF 计算量小，计算速度快，实时性好，且具有统计有效的特点。

本文提出一种基于EKF适用于机动目标的雷达测量数据抗野算法。利用新息［12］和新息方差来判别测量数据中的野值，若存在野值，在剔除野值后利用最小二乘法对目标的状态进行估计，消除了野值对EKF的影响。

2 目标运动模型

在目标跟踪过程中，建立符合实际，且便于数学处理的目标运动模型是跟踪算法能否获得应有的关键。由于各种因素的影响，要给出精确的目标运动方程描述十分困难。目前，常用的目标运动模型有：匀速（CV）模型、匀加速（CA）模型和匀速转弯（CT）模型。本文采用CV模型作为对雷达跟踪的目标的描述。

目标在三维空间中，系统的状态向量为

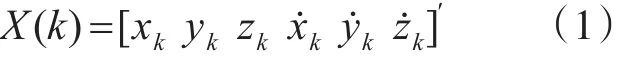
噪声向量为

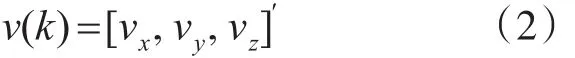
目标状态方程为

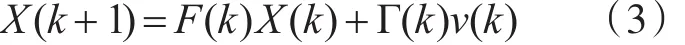
其中

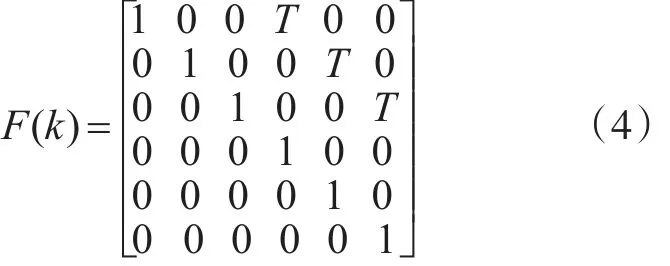
为系统状态转移矩阵

为过程噪声分布矩阵。

3 EKF算法原理

EKF算法的基本思想是对非线性函数的泰勒级数展开式进行线性化截断，从而将非线性问题转化为线性，再用线性估计的各种方法得到求解原非线性滤波问题的次优滤波算法。资料表明，二阶以上的EKF滤波性能与二阶相比没有明显提高，一般不选用，二阶EKF的性能比一阶EKF滤波性能好，但二阶EKF计算量远大于一阶EKF，因此一般情况下只采用一阶EKF。本文采用一阶EKF。

对于非线性系统，状态方程为

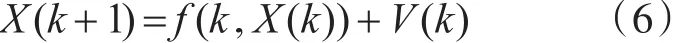
量测方程为

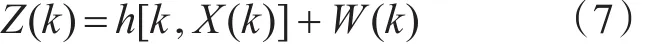
V(k)为具有协方差Q(k)的加性零均值白色过程噪声序列，即为具有协方差R(k)的加性零均值白色量测噪声序列，即

V(k)和W(k)彼此不相关，假定k时刻的估计为。对式（6）在附近进行泰勒级数展开，取其一阶项以产生一阶EKF：

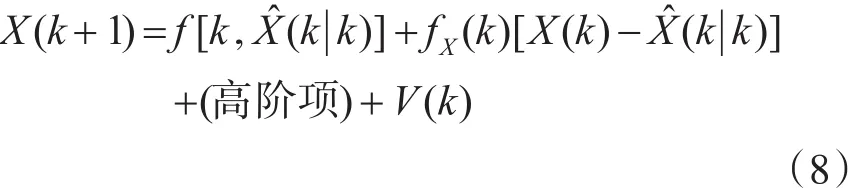
对式（8）取以Zk为条件的期望值，略去高阶项，状态的一步预测：

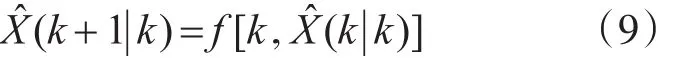
协方差的一步预测：

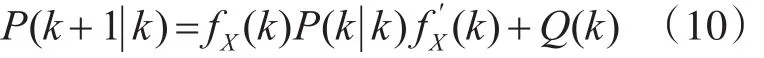
量测的预测值为

量测的预测值与量测值之间差值，即新息为

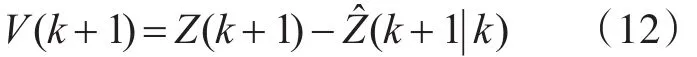
新息协方差为

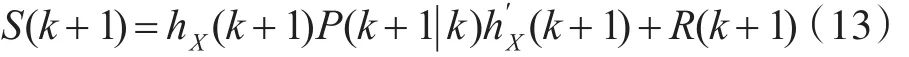
增益为

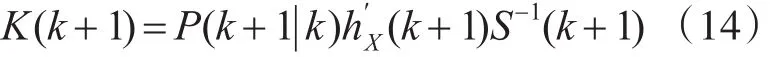
状态更新方程为

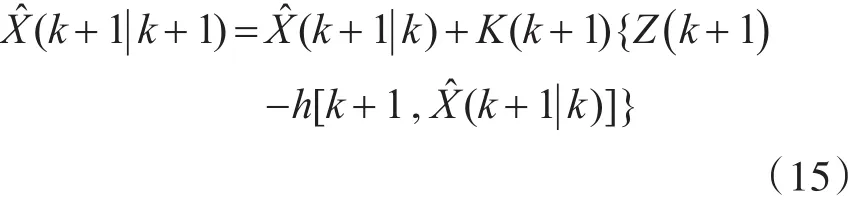
协方差更新方程为

4 野值的剔除及EKF的修正

4.1 剔除野值

不同的野值提出准则也会影响野值的剔除性能，选择合适的野值判别准则对野值的有效剔除很重要。目前，常用的野值判别方法主要分为以下几类：1）根据测量数据的统计特征，计算出标准差来设定阈值对野值进行判别，例如罗曼洛夫斯基准则、狄克松准则、格拉布斯等；2）通过信息处理技术判别野值，例如小波变换等；3）新息判别法。

第1）种方法阈值设定困难，且不适合动态测量的野值判别；第2）种方法算法复杂，在线估计困难；第3）种方法是根据滤波系统新息统计特征的变化，能动态判别测量数据中的野值，能实时处理。

新息直接反映了测量值的情况，如果测量数据中的某些数据是野值，则其所对应的新息会有较大的偏差。新息是零均的高斯随机向量。根据式（12）和式（13）可求得新息V(k+1)和新息协方差S(k+1)，利用新息的统计特性对Z(k+1)的每个分量进行判别，判别式为

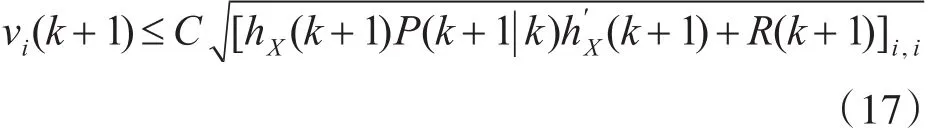
式中R(k+1)为量测噪声协方差矩阵，下角i表示矩阵对角线上第i个变元；vi(k+1)表示V(k+1)的第i个分量；C为常数，根据实际情况选取，一般选3或者4。若式（17）成立，则判别zi(k+1)为正常的测量值；若式（17）不成立，判zi(k+1)为野值，予以剔除，zi(k+1)是Z(k+1)的第i个分量。

4.2 修正算法

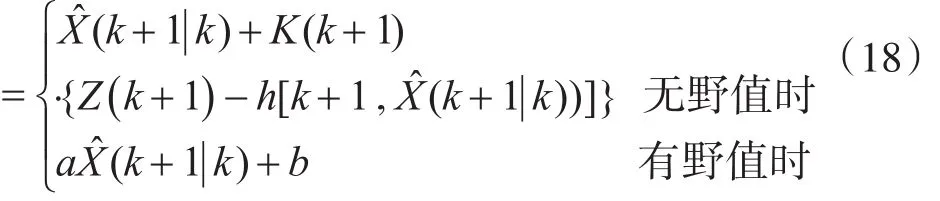
其中，a、b为待定参数。先求得前n组的状态一步预测值和状态估计值的平均值：

再利用最小二乘法估计参数a、b：

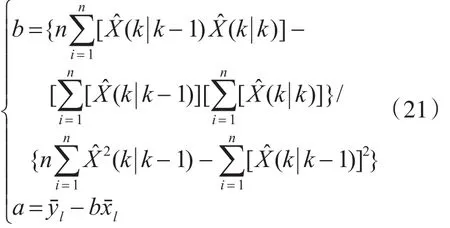
将求得的a、b的值代入式（18）就可以得到有野值时，修正后的EKF状态估计值。

5 实验仿真

噪声是高斯假设条件下，雷达跟踪以匀速运动的目标。距离测量误差的标准差为30m，方位角和俯仰角测量误差的标准差均为0.5°。目标的初始运动状态用式（3）描述，状态向量X(k)用式（1）表示，F(k)和 Γ(k)分别如式（4）和式（5）所示。目标的初始运动状态为

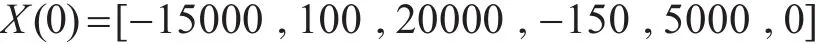
量测方程为如式（7），式中

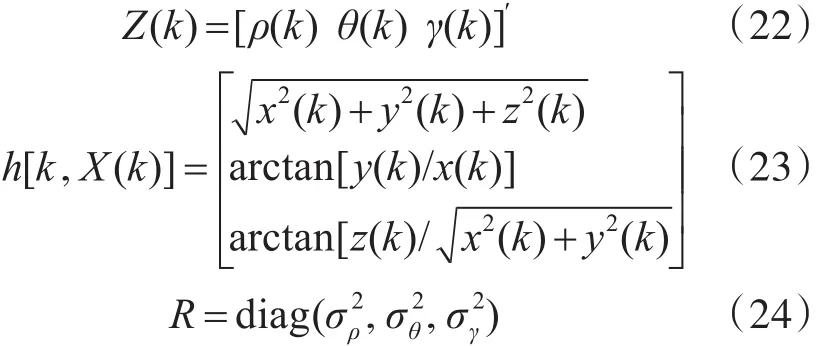
图1 原始误差误差

图2 剔野后的误差数据

由图1和图2可以看出，雷达测量数据中的野值被有效地提出，提高了目标跟踪的精度。

6 结语

本文利用扩展卡尔曼滤波过程中的新息特征，实时剔除机动目标的雷达测量数据中的野值。当雷达测量数据中存在野值，剔除野值后利用最小二乘法重新构造状态估计，消除了野值对扩展卡尔曼滤波的影响，提高了目标的跟踪精度。

［1］胡奎.一种新的雷达数据剔野方法［J］.飞行器测控学报，2012，31（6）：71-73.

［2］张亚松，任宏光.一种基于Kalman滤波的雷达数据抗野值方法［J］. 兵器装备工程学报，2016，37（2）：45-47.

［3］卢元磊，何佳洲，安瑾.目标预测中的野值剔除方法研究［J］.计算机与数字工程，2013，41（5）：722-725.

［4］卢元磊，何佳洲，安瑾等.几种野值剔除准则在目标预测中的应用研究［J］.2011，33（4）：98-102.

［5］宁倩慧，张艳兵，刘莉等.扩展卡尔曼滤波的目标跟踪优化算法［J］.探测与控制学报，2016，38（1）：90-94.

［6］卢迪，姚郁，贺风华.一种抗野值的Kalman滤波器［J］.系统仿真学报，2004，16（5）：1027-1029.

［7］程咏梅，潘泉，张洪才等.基于推广卡尔曼滤波的多站被动式融合跟踪［J］. 系统仿真学报，2003，15（4）：548-550.

［8］李硕，曾涛，龙腾等.基于推广卡尔曼滤波的机载无源定位改进算法［J］.北京理工大学学报，2002，22（4）：521-524.

［9］熊伟，陈立奎，何友等.有色噪声下的不敏卡尔曼滤波器［J］.电子与信息学报，2007，29（3）：598-600.

［10］张昆，陶建锋，李一立.基于粒子滤波的目标跟踪抗野值算法［J］.火力与指挥控制，2016，41（9）：98-102.

［11］刘凯，梁晓庚，李友年.基于粒子滤波的非线性目标跟踪算法研究［J］. 四川兵工学报，2014，35（11）：14-17.

［12］张强，孙红胜，胡泽明.基于新息协方差的机动目标轨迹估计算法研究［J］.信息工程大学学报，2012，13（7）：729-733.