基于能量法的起落架落震试验评定准则

杜金柱，孟凡星，卢学峰

沈阳飞机设计研究所 综合强度部，沈阳 110035

落震试验是一项常规的起落架动力学试验，原理是通过模拟飞机着陆的姿态、速度和质量等参数，获取起落架缓冲系统的动态特性。依据落震试验目的可分为选参试验和验证试验。选参试验的目的是依据研制指标和要求，通过落震试验确定缓冲系统的参数设计。验证试验是依据相关规范，对起落架动态特性进行验证。

起落架落震试验最早出现在二次世界大战，目的是以自由投放的形式获取飞机着陆载荷。国外学者对落震试验方法和相关问题进行了大量研究。其中，Flugge[1]建立了起落架着陆动力学模型，并在忽略水平载荷的情况下，研究了起落架在着陆和滑跑情况下的动力学方程及数值解法。文献[2-6]中进行了减缩质量法落震试验和仿升法落震试验的对比，并得出可用减缩质量法简化试验的结论。同时，研究了起转、回弹载荷，以及落震试验中机轮带转对水平载荷的影响[7-10]。国内，聂宏等基于仿真分析，研究了大型飞机及舰载机起飞、着陆拦阻等动力学过程[11-14]。牟让科等研究了油气式缓冲器的建模方法，并提出了仿升落震试验中当量升力的施加方法[15-16]。

飞机起落架落震试验是飞机研制及定型必要的试验环节，直接关系到飞机起落架设计能否满足设计要求。尽管美国军用标准和中国军用标准及民航适航条例都给出了明确的飞机起落架落震试验标准和要求[17-20]，但对减缩质量法和仿升法这两种落震试验的等价联系未有充分的论证和说明。本文以起落架典型的二自由度弹簧阻尼系统模型为研究对象，建立了适用于陆基飞机起落架的落震试验评定准则，该准则反应了起落架设计中对缓冲系统吸能、耗能、状态恢复及工作稳定性的要求。同时，给出了两种落震试验方法中耗能系数的计算方法，并分析了反行程阻尼系数和耗能系数之间的关系。最后，研究了两种落震试验方法的等价条件，得出了两种落震试验方法等价的前提是正反行程中耗散掉的能量相等，并进行了反行程阻尼系数与机轮不跳离台面的等效计算。

1 起落架落震试验能量分析模型

起落架缓冲系统包括机轮和缓冲器两部分,力学模型简化为二自由度弹簧阻尼系统。典型的起落架落震试验动力学模型如图1所示。

模型定义和假设条件如下：

1) 坐标系：模型坐标系中y轴向下，x轴向前，z轴按右手法则确定。

2)y1和y2为上部质量和机轮的垂向位移。

3) 起落架为典型的支柱式起落架，支柱无x方向和z方向的偏角。

4) 起落架动力学方程仅考虑上部质量和机轮的y向运动，无x和z方向的运动。

5) 能量分析中不考虑航向载荷做功情况，即假设支柱为刚体。

6) 机轮力学模型为线性弹簧，无阻尼，不消耗能量。

7) 仿升法中升力系数为1.0。

落震试验中，缓冲系统的工作分为压缩和反弹两个过程。压缩过程(正行程)中缓冲系统被压缩，机轮和缓冲器吸收能量。当系统的动能为零时，压缩过程结束，开始反弹过程(反行程)。反弹过程中，缓冲系统释放能量，上部质量向上运动。

压缩行程下沉速度对应的能量为

(1)

图1 起落架落震试验模型Fig.1 Model for landing gear drop test

式中：A为缓冲系统吸收的总能量；mdl为当量质量；Vy为下沉速度。

缓冲系统的机轮和缓冲器吸收的能量分别为

(2)

(3)

缓冲器吸收的能量比例为

(4)

式中：Atyre和Aabsorber为机轮和缓冲器吸收的能量；Ktyre为轮胎的刚度；ytyre为轮胎的压缩量；kabs为缓冲器吸收的能量占总能量的比例；Fs、Fa、Fh和Ff分别为缓冲器轴向载荷、空气弹簧力、油液阻尼力和缓冲器内部的摩擦力；s为缓冲器压缩行程；S为缓冲器压缩终点行程。

压缩过程中缓冲器消耗的能量为

(5)

反弹过程中缓冲器消耗的能量为

(6)

正反行程过程中缓冲器消耗能量总和为

Arh=Arh.c+Arh.e

(7)

热耗系数[21]定义为

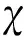
(8)

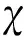
(9)

(10)

2 落震试验评定准则

落震试验中，起落架压缩和反弹过程本质上是动能、势能和热能的转换过程。从能量分析的角度可分为吸收能量、消耗能量、状态恢复能力和缓冲系统性能稳定性要求 4个方面。以下按此分类给出具体要求。

要求1 缓冲系统吸收能量要求：缓冲系统应能吸收规定下沉速度对应的能量，使用行程具有吸收使用功的能力，极限行程或结构行程具有吸收最大功的能力。

使用功情况需满足

A(Ssy)≥Asy

(11)

最大功情况需满足

A(Sstr)≥Amax

(12)

式中：

(13)

Amax=1.5Asy

(14)

其中：A(Ssy)为缓冲器压缩量为设计行程时缓冲系统吸收的能量；A(Sstr) 为缓冲器压缩量为缓冲器的结构行程或最大许用行程时缓冲系统吸收的能量;Ssy为缓冲器的使用行程；Sstr为缓冲器的结构行程或最大许用行程；Asy为使用功；Amax为最大功。

在吸收能量的同时，伴随有起落架压缩行程和载荷的限制。

缓冲器功量等式为

Aabsorber=ηaFyS

(15)

限制条件为

Fy≤Fy.limit

(16)

S≤Ssy

(17)

可推出：

(18)

式中：Fy为地面垂直载荷；ηa为缓冲器的效率系数；Fy.limit为垂直载荷限制值。

如果限定行程和载荷，即要求缓冲器的效率大于某一限定值。该值反映了起落架缓冲器吸收能量的水平，现阶段油气式缓冲器应达到70%以上[22]。

要求2 缓冲系统消耗能量的能力要求：该要求涉及起落架压缩过程和反弹过程。压缩过程中缓冲器吸收的能量大部分应转化为热能，以避免起落架伸出过程中释放能量而导致飞机反跳，同时起到降低起落架震荡的作用。

缓冲器消耗能量的能力用热耗系数表示，陆基飞机不单独对正反行程耗能能力提出单独要求，而是整体评估正反行程的耗能能力。缓冲器消耗能量的比例应在0.65～0.85的范围内[23]，即

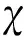
(19)

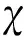
缓冲系统消耗能量的能力用耗能系数表示，定义为

(20)

式中：λmin为满足设计的最低值。

要求3 状态恢复能力要求：缓冲系统应在规定的时间内完成吸能和耗能的物理过程，并及时恢复到全伸长状态，以吸收二次撞击的能量。规范要求正反行程时间不大于0.8 s(即满足式(21))。该要求说明了缓冲器的阻尼不能以消耗能量为目的无限制地增大。要求3与要求2存在相互制约的关系。

T≤0.8

(21)

式中：T为正反行程总的时间。

要求4 缓冲系统性能稳定性要求：起落架系统应是稳定的。稳定性体现在连续投放过程中起落架的工作特性应无明显变化。起落架落震多次投放试验中要求测量参数变化的比例不超过10%，即

(22)

式中：P为落震试验中的稳定性控制参数;Pi和Pj为参数P的第i、j次测量值。

以上4条要求中，要求1和要求4在试验中可直接应用。要求2和要求3需要结合具体的试验，依据能量等效进行转化。

3 仿升法落震试验耗能分析

由于试验中无法直接测量油液阻尼力和摩擦力。本文提出反行程阻尼系数的概念，并使用该参数来确定缓冲器消耗能量的能力，相关参数如图2所示(图中ygc为重心位移)，其公式为

(23)

(24)

式中：t0为活塞杆由压缩终点起到全伸长的时间；t1为反行程开始到轮胎二次接地的时间；Δt为反行程结束到重心到达最高点的时间；tt为重心开始下落到轮胎触地时间；kt为比例系数。

图2 反行程阻尼系数Fig.2 Anti-stroke damping coefficient

反弹过程能量转换过程为

(25)

式中：g为重力加速度；ht为起落架反弹高度。

将式(1)代入式(25)，可得起落架反弹高度为

(26)

因有

(27)

可推出

(28)

将式(23)展开，可得

(1-ζ)t0=ζkttt

(29)

将式(29)代入式(28)，整理得

(30)

可推出

(31)

若给定：

ζ≥ζmin

(32)

可推出

(33)

若kt≥1.0，有：

(34)

式中：ζmin为满足设计要求的反行程阻尼系数的最小值。

依据式(33)绘制热耗系数和t0的关系曲线，kabs取0.85，ζmin取0.7，Vy=3.3 m/s，kt分别取0.8、1.0和1.2，绘制曲线如图3所示。

图3 热耗系数-反行程时间关系曲线Fig.3 Curves of heat dissipation coefficient vs extented time

热耗系数和耗能系数反映的是耗能的最低要求，为了综合评定缓冲系统的吸能和耗能能力，图3中引入起落架“耗能能力”曲线和0.8 s限制线，分别为图3中曲线a和曲线c。曲线b是kt=1.0时热耗系数和反弹时间的关系。

“耗能能力”曲线可表示为反行程时间的函数，其表达式为

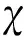
(35)

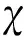
可见，仿升试验中反行程阻尼系数的根本要求就是在保证活塞杆及时伸出的前提下，消耗的能量大于给定的设计值。

4 减缩质量法落震试验耗能分析

减缩质量法落震试验取3个典型状态进行分析：Ⅰ为缓冲器和轮胎均未压缩，但轮胎接触地面的初始状态；Ⅱ为缓冲器和轮胎达到最大压缩量状态；Ⅲ为反弹过程中上部质量回到零点，但机轮未离开地面状态，该状态为机轮跳离台面的临界状态。

减缩质量法落震试验反弹控制中要求机轮不允许跳离地面。若达到此要求，起落架缓冲系统必须满足以下两点要求:

1) 落震试验正反行程中，缓冲系统消耗足够多的能量，确保上部质量不回跳过零点，即位移不能小于0。否则，由于上部质量向上运动，轮胎将被带离向上运动，跳离地面。

2) 缓冲器在反行程的开始阶段有合适的能量来抑制轮胎的振动，确保反行程中轮胎释放的能量小于缓冲器释放的能量对机轮做的功。

要求1)本质上是缓冲器消耗能量指标的要求。以下分析要求1)需要的热耗系数。

取状态Ⅱ，缓冲器系统吸收的能量为投放质量具有的动能与压缩过程中重力做功之和，即

(36)

式中：mtf为减缩质量法落震试验中的投放质量。

取状态Ⅲ，若轮胎不跳离地面，要求上部质量的速度必为零，说明消耗的能量与状态Ⅰ所具有的动能相等，即

(37)

联立状态Ⅱ和状态Ⅲ的方程式(36)和式(37)解得

(38)

令

(39)

要消耗掉足够的能量以控制上部质量不回跳，可推出

(40)

式(40)的物理意义：说明若要机轮不跳离地面，缓冲系统消耗的能量要大于临界值Ccr，临界值由下沉速度和重心位移最大值决定。

由于不同起落架的位移存在差异，热耗系数和位移之间的关系转换为热耗系数和缓冲系统过载之间的关系。

由

(41)

可推出：

(42)

代入热耗系数计算公式式(38)得：

(43)

可推出：

(44)

式中：η为缓冲系统效率系数；n为着陆过载；λ为缓冲器消耗能量与缓冲系统吸收能量比例。

若给定缓冲器吸收功量比例kabs和缓冲系统效率系数η可绘制热耗系数和过载之间的关系曲线。缓冲系统效率系数取0.7，缓冲器吸收功量比例kabs变化范围取0.60～0.85，热耗系数和过载的关系曲线如图4所示，缓冲系统耗能系数与过载的关系曲线如图5所示。

要求2)可计算耗能上限，取机轮即将跳离台面的临界状态进行分析。反弹过程中缓冲器对机轮做功，并假定反行程缓冲器载荷如图6所示。同时，分析中忽略机轮的重量。

反行程过程中上部质量的动能为

(45)

图4 热耗系数与过载的关系曲线Fig.4 Curves of heat dissipation coefficient vs load factor

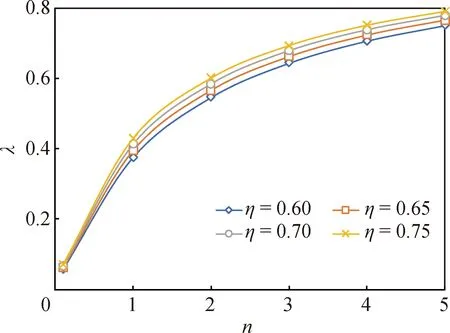
图5 耗能系数与过载的关系曲线Fig.5 Curves of energy dissipation coefficient vs load factor

图6 反行程过程中的载荷-行程关系曲线Fig.6 Curves of load vs stroke in extended process

式中：

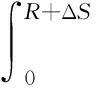
(46)

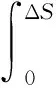
(47)

由缓冲器载荷假设，可得

(48)

其中：AΔS-Arh.ΔS为ΔS行程范围内缓冲器释放的能量；β为图6中缓冲器载荷包络面积与三角形面积的比值;ΔS为缓冲器反行程伸展量；R为轮胎压缩量；v为上部质量的速度。

将式(46)～式(48)代入(45)可推出

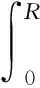
(49)

引入机轮不跳离台面的条件，即

(50)

将式(50)代入式(49)，可得：

(51)

式(51)中速度v取0，可简化为

Atyre+(AΔS-Arh.ΔS)≤mtfg(R+ΔS)

(52)

将ΔS和R表示为行程的函数，即

ΔS=ksS

(53)

R=katS

(54)

式中：kat为缓冲器与轮胎的刚度比；ks为反行程伸展量与压缩终点行程的比值。

将式(53)和式(54)代入式(52)，可得

(55)

将式(55)整理，可得

(56)

由于

A=mdlgh

(57)

可推出

(58)

由于

(59)

式中：h为落震试验投放高度。

(60)

令

(61)

进而可以确定热耗系数的上限为

(62)

式中：ηa为缓冲器的效率系数。

综合要求1)和要求2)，可以确定缓冲器消耗能量的范围，既要大于限定值，又不能过大。

减缩质量法落震试验中，若仅采用投放质量重心位移用以确定反弹高度，在重心满足要求的情况下，活塞杆的伸出量可能很小，没有足够的能力迎接下一次撞击，导致二次撞击的载荷较大。故需要另外再引入一个参数来表征活塞杆的伸出量。这样就需要两个参数：一个用来判定重心的反弹高度，一个用来判定活塞杆的伸出长度。在重心不回跳且具有最大活塞杆伸出量的情况下可以判断出机轮不跳离台面。对机轮的位移控制达到了同时控制弹簧支撑质量和活塞杆伸出量的目的，等效于耗能和正反行程时间小于0.8 s这两条要求。

5 减缩质量法与仿升法的等价关系

两种落震试验反弹控制的目的是相同的，但二者不应理解为完全等价。二者建立等价关系的前提是两种落震方法是等价的。NACA进行过此类对比试验，试验结果表明：在正行程阶段，两种落震方法的效果在工程上是一致的、可接受的。等价关系是基于吸收的能量相等建立的[3]。

若能将等价的条件扩展到反行程，即正反行程消耗的能量也相同，即可认为在正反行程过程中均存在能量等价关系。两种试验方法中反行程消耗能量的过程显然是不同的，无法直接建立等价关系。若认为是等价的，只能是反行程耗能影响较小的情况，大部分能量在正行程过程中消耗掉。这种情况是存在的，英国规范Def.Stan.00-970中要求缓冲器消耗的能量越多越好，在正行程中至少要消耗掉67%的能量[24]，这样反行程耗能的影响将较小，两种落震方法得到的耗能水平是接近的，可以建立反弹控制的等价关系。

取消耗的能量水平相等，即

(63)

可推出

(64)

取n=2，η=0.7，Vy=3 m/s,t0=0.4 s，kt=1，可得

(65)

对于在反行程耗能比例较大的起落架，两种落震方法得到的起落架反行程工作特性差异较大，需要仿真计算确定两种方法反弹控制的差异，不应直接认为等效，且使用减缩质量法考核。

6 结 论

1) 对于陆基飞机，建立了一套适用于起落架落震试验评定的准则。该准则反映了起落架缓冲系统吸收和消耗能量等方面的能力，同时也解释了落震试验参数控制的目的和原理。

2) 建立了在两种落震试验方法中进行耗能系数计算的方法，并计算了反行程阻尼系数和耗能系数之间的关系。定量地给出了轮胎反弹控制和耗能指标之间的关系。

3) 分析了两种落震方法在工程上等效的范围和条件。并对典型情况进行了计算，得到减缩质量法落震试验机轮不跳离台面等效于仿升法落震试验时的反行程阻尼系数为0.67。

4) 该评定准则反应设计要求的集合，且是开放的体系。舰载机落震试验不能简单地直接借用陆基飞机的评定准则，需要补充舰载机起落架缓冲系统相关的设计要求方可使用。

[1] FLUGGE W. Landing-gear impact: NACA TN 2743[R]. Washington, D.C.: NASA, 1952.

[2] MILWITZKY B, COOK F E. Analysis of landing-gear behavior: NACA TN 2755[R]. Washington,D.C.: NASA, 1952.

[3] MILWITZKY B, LINDQUIST D C. Evaluation of the reduced-mass method of representing wing-lift effects in free-fall drop tests of landing gears: NACA TN 2400[R]. Washington, D.C.: NASA, 1951.

[4] MILWITZKY B, LINDQUIST D C, POTTER D M. An experimental investigation of wheel spin-up drag loads: NACA TN 3248[R]. Washington, D.C.: NASA, 1954.

[5] LINDQUIST D C. Effects of wing lift and weight on landing-gear loads: NACA TN 2645[R]. Washington, D.C.: NASA, 1952.

[6] LINDQUIST D C. A statistical study of wing lift at ground contact for four transport airplanes: NACA TN 3435[R]. Washington, D.C.: NASA, 1955.

[7] FLUGGE W, COALE C W. The influence of wheel spin-up on landing-gear impact: NACA TN 3217[R]. Washington, D.C.: NASA, 1954.

[8] POTTER D M. An experimental investigation of the effect of wheel prerotation on landing-gear drag loads: NACA TN 3250[R]. Washington, D.C.: NASA, 1954.

[9] MILWITZKY B, COOK F E. Effect of interaction on landing-gear behavior and dynamic loads in a flexible airplane structure: NACA TN 3467[R]. Washington, D.C.: NASA, 1955.

[10] HOOTMAN J A, JONES A R. Results of landing tests of various airplanes: NACA TN 863[R]. Washington, D. C.: NASA, 1942.

[11] 魏小辉, 刘成龙, 聂宏, 等. 半轴式起落架落震动力学及结构参数影响研究[J]. 振动工程学报, 2014, 27(1): 40-45.

WEI X H, LIU C L, NIE H, et al. Study on drop dynamics and the influence of structural parameters on half-axle landing gear[J]. Journal of Vibration Engineering, 2014, 27(1): 40-45 (in Chinese).

[12] 聂宏, 魏小辉. 大型民用飞机起落架关键技术[J]. 南京航空航天大学学报, 2008, 40(4): 427-432.

NIE H, WEI X H. Key technologies for landing gear of large civil aircrafts[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2008, 40(4): 427-432 (in Chinese).

[13] 刘晖. 起落架缓冲系统特性及其半主动控制技术研究[D]. 南京: 南京航空航天大学, 2007: 13-26.

LIU H. Research on property and semi-active control of landing gear shock absorption system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2007: 13-26 (in Chinese).

[14] 晋萍, 聂宏. 起落架着陆动态仿真分析模型及参数优化设计[J]. 南京航空航天大学学报, 2003, 35(5): 498-502.

JIN P, NIE H. Dynamic simulation model and parameter optimization for landing gear impact[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2003, 35(5): 498-502 (in Chinese).

[15] 牟让科, 齐丕骞, 吴启荣, 等. 一种自适应双腔缓冲器动力特性研究[J]. 应用力学学报, 2001, 18(z1): 96-100.

MU R K, QI P Q, WU Q R， et al. Investigation for the dynamic behavior of a dual chamber energy-absorber with adaptive control[J]. Chinese Journal of Applied Mechanics, 2001, 18(z1): 96-100 (in Chinese).

[16] 豆清波, 史惟琦, 牟让科, 等. 基于落震试验的油-气式起落架气体压缩多变指数变化规律研究[J]. 实验力学, 2015, 30(2): 215-220.

DOU Q B, SHI W Q, MU R K， et al. On the gas compression polytropic index variation of oil-gas type landing gear based on drop test[J]. Journal of Experiment Mechanics, 2015, 30(2): 215-220 (in Chinese).

[17] 金秀芬, 李凯. 起落架落震试验修正案影响分析及验证思路研究[J]. 航空工程进展, 2012, 3(4): 453-456.

JIN X F, LI K. Impact analysis and investigation of compliance approach for the landing gear drop test amendment[J]. Advances in Aeronautical Science and Engineering, 2012, 3(4): 453-456 (in Chinese).

[18] 王海涛, 李成行. 运输类飞机起落架落震试验适航条款更改及分析[J]. 航空工程进展, 2010, 1(4): 365-368.

WANG H T, LI C X. Amendment and analysis of airworthiness regulations for landing gears’ falling vibration tests in transport category airplanes[J]. Advances in Aeronautical Science and Engineering, 2010, 1(4): 365-368 (in Chinese).

[19] 蒋祖国, 周占廷, 舒成辉, 等. 我国现有飞机强度规范的更新和发展[J]. 航空学报, 2003, 24(4): 339-341.

JIANG Z G, ZHOU Z T, SHU C H, et al. Updating and developing of the current aircraft strength specification in China[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(4): 339-341 (in Chinese).

[20] 中国民用航空总局. 中国民用航空规章第25部——运输类飞机适航标准[S]. 北京: 中国民用航空总局, 2008.

Civil Aviation Administration of China. Civil aviation regulation, Part 25 Air worthness standards: Transport category airplanes[S]. Beijing： Civil Aviation Administration of China, 2008 (in Chinese).

[21] 郦正能. 飞行器结构学[M]. 北京: 北京航空航天大学出版社, 2010: 369-371.

LI Z N. Aircraft structure[M]. Beijing： Beihang University Press, 2010: 369-371 (in Chinese).

[22] 航空工业部科学技术委员会. 飞机起落架强度设计指南[M]. 四川： 四川科学技术出版社， 1989: 632-634.

Science and Technology Committee of Aeronautics and Astronautics. Introduction to design for airplane landing gear[M]. Chengdu: Sichuan Science and Technology Press, 1989: 632-634 (in Chinese).

[23] 《飞机设计手册》总编委会. 飞机设计手册第 14分册：起飞着陆系统设计[M]. 北京: 航空工业出版社, 2002: 680-762.

The Chief Committee of Aircraft Design Manual. Aircraft design manual Vol. 14： Takeoff and landing system design[M]. Beijing： Aviation Industry Press, 2002: 680-762 (in Chinese).

[24] DENIS H. Aircraft loading and structure layout[M]. Reston, VA: AIAA, 2004: 222-223.