超临界压力下碳氢燃料裂解与流动传热模拟的快速算法

黄世璋，阮波，高效伟，刘华雩

大连理工大学 航空航天学院，大连 116024

超燃冲压发动机是高超声速飞行器的理想动力装置，具有良好的军事和民用价值，受到了世界各国的重视。由于飞行速度快，飞行器受到气动加热和燃烧释热的双重作用，发动机热防护性能亟待提升。采用吸热型碳氢燃料作为冷却剂的主动再生冷却技术是目前最有效的冷却方式之一，在超燃冲压发动机热防护中发挥着重要作用[1-2]。主动再生冷却技术是利用吸热型碳氢燃料的对流传热来实现对发动机的冷却，而高分子碳氢燃料的热裂解化学反应吸热可明显提升燃料的冷却能力[3-5]。此外，裂解反应产生的小分子碳氢化合物燃烧反应速度快，也是提高燃烧性能的关键[6-8]。因此准确预测超燃冲压发动机冷却通道中燃料的裂解特性对超燃冲压发动机的设计非常关键。

研究碳氢燃料裂解特性需要建立可靠的化学反应机理，国内外对此进行了大量研究。Zhong等[9-10]对压力为3.5～4.5 MPa、温度为700～1 100 K条件下的RP-3航空煤油热裂解反应进行了实验研究，得到了煤油热解产物的分布特性，在此基础上建立了一步总包反应机理。Jiang等[11]对RP-3航空煤油在5 MPa下的传热和裂解现象开展了详细的实验研究，提出了适用于航空煤油的详细化学反应机理。Stewart等[12]研究了超临界十氢化萘、四氢化萘和正癸烷的热解反应，获得了主要的裂解产物分布并建立了一步总包反应机理。Ward等[13-14]对正癸烷裂解与传热过程进行了实验研究，并采用成比例产物分布(Proportional Product Distribution, PPD)化学模型建立了适用于压力在3.45～11.38 MPa范围内正癸烷轻度裂解的一步总包反应机理，即平均PPD机理。Zhu等[15]也对超临界压力正癸烷的轻度裂解和传热现象开展了实验研究，基于实验结果提出了一步总包反应机理。

在建立反应机理的基础上，数值模拟已成为研究碳氢燃料裂解与传热的重要手段。从基础研究方面来看，正癸烷与真实煤油热物性非常相似[16]，因此许多学者采用正癸烷作为航空煤油的替代燃料来研究吸热型碳氢燃料的超临界传热与裂解吸热反应的耦合作用机制。阮波和孟华[17]建立了通用的碳氢燃料裂解混合物物性计算方法，进一步基于平均PPD反应机理[14]建立了考虑正癸烷裂解吸热及超临界传热现象的数值计算模型，通过与已有的实验和数值计算结果比较，验证了数值模型的可靠性。Bao等[4]模拟了三维冷却通道内正癸烷的裂解传热现象，分析了温度、速度和正癸烷质量分数在冷却通道内的分布。与不考虑裂解情况相比，裂解反应使得流场温度和燃料热沉在截面上的分布变得更均匀。Zhang等[18]研究了冷却通道横截面高宽比对正癸烷裂解和传热过程的影响。增大高宽比后通道内出现明显的热分层和裂解度不均匀现象，不利于燃料化学热沉的利用。Feng等[19]对圆管内超临界压力正癸烷的裂解与流动传热进行了数值模拟，分析了管内传质传热与裂解反应的相互影响机制。

由于裂解产物的复杂性，即便采用简化反应机理，其巨大的计算开销依然是进行大规模数值研究的主要困难。目前提高计算效率的主要途径有物性快速算法和反应机理简化方法。刘志琦[20]基于SUPERTRAPP软件生成的三维物性数据库，建立了高效查表方法，显著提升了正癸烷裂解传热计算效率。程泽源和朱剑琴[21]建立了低裂解度正癸烷物性快速算法，并分析了算法的效率和精度。Ruan等[22]对平均PPD机理[14]进行了简化，提出了一个12组分的模型，该模型在保证精度的前提下具有更高的计算效率。物性快速算法会提升计算效率，然而仍需求解数目庞大的组分输运方程；反应机理简化会减少组分输运方程数量，但受精度限制简化程度始终有限。

本文在前期研究的基础上[17]，通过数值分析和理论推导对算法进行改进和优化，建立了一套快速算法。与目前已有的求解全组分输运方程的算法相比，该快速算法只需求解1个组分输运方程，但是依然考虑了各组分的输运过程。通过与全组分输运方程算法以及现有的实验和数值结果进行对比，全面考察了算法的计算效率和精度。最后采用该算法对三维矩形截面冷却通道内的正癸烷裂解和传热过程进行数值模拟研究。该方法的建立对于提高碳氢燃料裂解与传热数值模拟的计算效率具有重要意义。

1 数值模型

1.1 守恒方程

本文研究碳氢燃料裂解吸热化学反应与湍流传热的耦合过程，在数值模拟过程中，需要求解连续性方程、动量方程、组分输运方程、能量方程以及湍流控制方程。

连续性方程：

(1)

式中：ρ为流体密度；u为速度。

动量方程：

(2)

式中：p为压力；τeff为黏性应力张量。

组分输运方程：

(3)

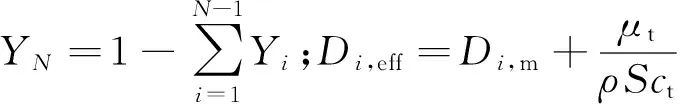
(4)

能量方程：

(5)

式中：etol为总内能；T为温度；λ为导热系数；cp为定压比热；Prt=0.85为湍流普朗特数。

标准k-ε湍流控制方程：

(6)

(7)

式中：k为湍动能；ε为耗散率；μ为黏性系数；Gk为湍动能生成项；σk、σε为k-ε方程的普朗特数；C1=1.44和C2=1.92为常数。为了准确捕捉近壁面参数变化，采用了强化壁面处理。当计算网格足够密，可以直接求解黏性底层时，近壁面采用适用于低雷诺数的一方程Wolfstein湍流模型，否则使用壁面函数计算。

1.2 物性计算方法

超临界状态下流体的物性随着压力和温度发生剧烈变化，而流体物性变化与其裂解吸热/流动传热过程是紧密耦合在一起的，因而物性的准确计算对超临界压力碳氢燃料裂解与传热的研究十分关键。修正的对应态(Corresponding-State) 方法[23-24]是计算流体混合物密度、导热系数和黏性系数的普适方法。选择丙烷作为参考物质，采用修正的对应态方法计算混合物密度和输运系数。流体的焓值和定压比热通过基本的热力学关系式以及Soave-Redlich-Kwong(SRK) 状态方程计算得到[25]。对于质量扩散系数的计算，首先采用Fuller经验公式计算低压下的二元质量扩散系数，然后再通过 Takahashi建议的对比态方法来考虑压力的影响[26]。各物性的详细计算方法及其可靠性验证可参考文献[17, 27]。

1.3 化学动力学模型

碳氢燃料在高温条件下发生裂解反应，高分子碳氢燃料的裂解反应的详细机理非常复杂，涉及成百个基元反应和上千种组分，以目前的计算条件采用详细机理进行化学反应流动模拟非常困难，因此进行数值模拟通常采用简化的反应机理。本文选择目前使用较为广泛的一步总包化学反应模型。Ward等[14]提出的PPD化学模型，适用于压力在3.45～11.38 MPa范围内的轻度裂解。根据实验结果和质量守恒原理得到总包化学反应机理为[22, 27]

C10H22→0.153CH4+0.222C2H4+0.138C2H6+

0.200C3H6+0.185C3H8+0.171C4H8+

0.118C4H10+0.149C5H10+0.137C5H12+

0.170C6H12+0.106C6H14+0.147C7H14+

0.091C7H16+0.132C8H16+0.040C8H18+

0.046C9H18+0.031C9H20

该反应速率常数由Arrhenius公式kA=A·exp(-Ea/RT)计算，其中指前因子A=1.6×1015s-1，活化能Ea=263.7 kJ/mol，R为普适气体常数。

1.4 数值格式与收敛准则

以上热物性计算方法以及化学动力学模型通过用户自定义函数(User Defined Function, UDF)编程的方式建立在商用计算流体力学(CFD)软件ANSYS FLUENT 13.0中。在本文数值模拟中，对流项离散采用二阶迎风格式，黏性项采用中心差分格式，压力-速度耦合采用Coupled算法。控制方程求解收敛判断条件为方程残差<10-5，同时监控进出口流量、出口温度、速度、重要组分质量分数及压力值变化直至其趋于稳定。

2 快速算法的构建

基于以上理论，在前期的工作中已经建立了完整的模拟超临界压力碳氢燃料裂解与传热的数值方法[17]，并成功用于超临界压力正癸烷裂解吸热/流动传热的模拟研究，充分验证了算法和程序的可靠性[22, 27]。前期的数值方法包含完整的组分输运方程，通过各组分源项来考虑化学反应的影响，并且准确考虑了各组分之间的扩散效应。本文在前期算法的基础上，通过数值分析和理论推导进行算法改进和优化，从而建立一种新的快速算法。

高分子碳氢燃料裂解产物组分很多，求解完整的组分输运方程给数值模拟带来很大的挑战。此外，混合物的物性计算过程非常复杂，而且在CFD求解过程中需要进行多次迭代才能满足流场收敛条件，其中每次迭代过程中所有控制体内的物性均需要重新进行计算，这必然会消耗大量的时间。本文将分别对这两方面进行优化和改进以提高计算效率。

2.1 热物性查表法

(8)

式中：下标“o”表示物性库起始点的状态：po=3 MPa，To=300 K，αo=0；Δp=0.2 MPa；ΔT=2 K；Δα=1%。

CFD求解过程中，通过控制体内的p、T、α和式(8)确定该状态点在物性库中对应的位置，再通过线性插值得到物性。需要说明的是，该物性库存储仅需要占用大约75 MB内存，对硬件资源需求很小。

为了比较物性查表法与直接计算方法的计算效率，总共计算了2 383 101个状态的物性：温度为500～1 200 K, 间隔0.5 K；压力为3～5 MPa，间隔0.1 MPa；裂解率为0～40%，间隔0.5%。计算所用时间如表1所示。由于直接法需要进行2 383 101次混合物物性求解，而查表法每次计算只需进行线性插值，因此查表法比直接法计算效率有数量级的提升。

表1 热物性计算时间对比

进一步考察查表法的精度。采用上述各个工况下的计算结果分析查表法的精度，与直接计算结果相比误差均在±0.4%以内。因此，本文建立的物性库查表法精度是可以满足数值模拟需求的。

2.2 组分输运方程的快速求解方法

2.2.1 组分输运特性分析

当分子数密度存在空间不均匀性时，由于分子的热运动或湍流脉动而发生的质量输运，称为扩散现象。这种输运特性由组分输运方程体现。精确考虑各个组分之间的扩散特性需要求解完整的组分输运方程[17]。对于混合物组分非常多的情况，这必然会带来很大的计算开销。因此，如果能够建立一种简单且能保证精度的计算方法，对提高计算效率有非常重要的意义。本节主要分析超临界压力下正癸烷裂解反应流动中的组分扩散规律，从而寻找一种简单有效的组分扩散计算方法，为组分输运方程的简化提供依据。

首先选择图1所示模型分析超临界压力正癸烷裂解产物的组分输运特性。采用轴对称模型进行计算。图中O为坐标原点；x和r分别为轴向和径向坐标。计算工况为[14]：入口温度T0=473 K；入口压力p0的范围为3.45～11.38 MPa；流量m=0.5 mL/min。壁面温度Tw沿x方向的变化函数为f(x)，其中最高壁温Tw_max=873 K。在进行网格无关性验证后选择30×1 000网格进行计算。

图1 计算模型示意图Fig.1 Schematic of computation model

对于冷却通道内碳氢燃料裂解反应流动问题，入口处燃料温度低于裂解发生的温度，随着壁面加热，近壁面燃料温度首先升高至裂解所需温度进而发生裂解，从而各组分沿垂直壁面方向产生浓度梯度，发生扩散现象。影响扩散特性的参数为有效扩散系数Di,eff，如式(3)所示。Di,eff由湍流扩散系数μt/ρSct和分子扩散系数Di,m两部分组成。研究发现湍流区的湍流扩散系数通常在10-6m2/s量级以上，而超临界碳氢燃料分子扩散系数均在10-7m2/s量级，因此在湍流状态下，μt/ρSct≫Di,m,组分输运由湍流扩散系数主导，分子扩散系数影响忽略不计[13, 14]。但是在黏性底层组分输运由分子扩散主导，因此分子扩散的准确计算会直接影响近壁面流场的计算精度。图2为分子扩散系数随温度和压力的变化特征(图中黑色实线为温度等值线)，在液态区域(T<618 K)为10-8m2/s量级，超临界状态时为10-7m2/s量级，这与文献[28]中的结论完全吻合。此外，各组分的分子扩散系数随温度的升高而增大，随压力的增大而减小。

为了考察黏性底层内的扩散特性，在1.0×10-8～1.0×10-6m2/s范围内选择不同分子扩散系数进行数值模拟，并与直接计算分子扩散系数时的模拟结果进行对比。数值研究发现，在该范围内分子扩散系数对轴线上的计算结果几乎没有影响，如图3(a)、图3 (b)所示(图中xi为组元i的摩尔分数；Dij为二元质量扩散系数[17])，进一步说明湍流区分子扩散系数的影响是可以忽略不计的。然而在近壁面黏性底层区域，由于不存在湍流扩散，分子扩散系数直接影响组分输运能力，如图3(c)、图3 (d) 所示。研究发现黏性底层内组分输运能力和浓度对分子扩散系数是比较敏感的。

考虑到在中轻度裂解条件下正癸烷浓度远大于其他产物浓度，因此其输运特性对流场影响最大。此外，各组分扩散系数随温度和压力的变化规律相似(如图2所示)，因此将各组分扩散系数统一选择为正癸烷扩散系数，即

Di,m=DC10H22,mi=1～N

(9)

则会减小数值模拟与真实物理过程的误差，保证各压力和温度下近壁面组分扩散的计算精度。

数值模拟时，分别采用简化计算(式(9))与直接计算两种方法确定分子扩散系数，得到的壁面处质量分数对比情况如图4所示。结果表明该简化计算方法在各个压力下均可准确模拟出壁面组分浓度，说明采用该方法确定分子扩散系数是合理的，具有较宽的适用范围。

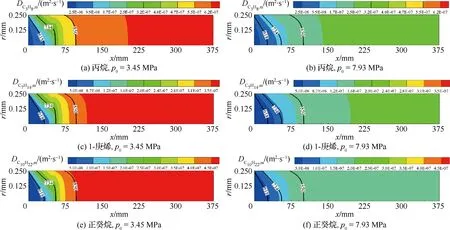
图2 不同压力下各组分的分子扩散系数分布Fig.2 Distributions of molecular diffusion coefficients for various species under different pressures

图3 分子扩散系数对计算结果的影响(p0=3.45 MPa)Fig.3 Effect of molecular diffusion coefficient on simulation results (p0=3.45 MPa)

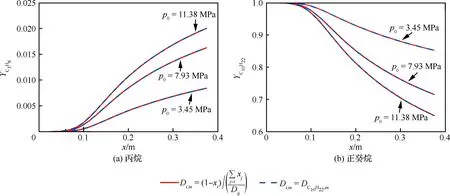
图4 不同压力下壁面处组分质量分数Fig.4 Species mass fraction at tube wall under different pressures

2.2.2 组分输运方程的简化及其理论基础

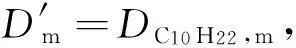
A(Yi)=Si

(10)

式中：算子A的形式为

A=

(11)

如果满足下列两个条件：

条件1 对于任意裂解产物a和b，在整个流场域内

(12)

恒成立，其中θ为常数。

条件2 在流场边界上

(13)

式中：Ω1为入口边界；Ω2为除入口之外的其他边界；n为流场边界外法向；x为求解域空间坐标。

那么组分输运方程的解必满足：

Yb=θYa

(14)

其数学证明见附录A。

对于条件1，由于本文采用一步总包PPD机理，各组分化学反应源项严格成比例，因此该条件是成立的。采用CFD技术模拟化学反应流场最为常用的壁面边界条件为非催化壁面，即∂Yi/∂n=0;对于冷却通道内的流动问题，入口边界上(Ω1)所有裂解产物满足Yi=0；出口处采用零梯度∂Yi/∂n=0处理；对于轴对称或对称模型，在对称轴或对称面上也满足∂Yi/∂n=0。因此，对于冷却通道内的流动问题条件2也是成立的。综上所述，采用一步总包反应机理模拟冷却通道内的裂解与流动问题，结论(式(14))是成立的。

根据该结论，只需要求解其中一个产物(例如产物a)的组分输运方程的解，其他产物(例如产物b)组分输运方程的解可通过式(14)确定。因此将需要求解的守恒方程数量从24(7+17)个减少到8(7+1)个，必然会大幅度提升计算效率。

3 数值结果与分析

3.1 计算效率和精度分析

基于第2节的理论分析，采用物性查表和组分输运方程简化方法，建立了碳氢燃料裂解和对流传热分析的快速算法。为了便于比较不同算法的计算效率和精度，本文以STE(Species Transport Equations)、DC(Direct Calculation)和LT(Look-up Table)分别代表组分输运方程、物性直接计算和物性查表，则“17STE(DC)”代表“17个组分输运方程(物性直接计算)”方法，即文献[17]中求解全组分输运方程的算法，本文称之为“全组分算法”；“1STE(LT)”代表“1个组分输运方程(物性查表)”方法，为本文改进和优化后的快速算法。

分别采用两种算法对文献[13-14]中的模型(图1所示)进行计算，以最高壁温为873 K、质量流量为0.5 mL/min、压力为3.45 MPa的工况为例，分析不同算法的计算效率。该算例计算硬件为主频3.6 GHz的台式机，采用单核进行计算。迭代2 000步流场收敛，计算时间如表2所示。通过对比可以看出，快速算法计算效率比全组分算法提高约22.41倍。计算效率的提高由两部分组成，其中物性库查表方法使计算效率提升约3.35倍，而组分输运方程的简化使计算效率提升约6.68倍。由于快速算法只需要求解一个组分输运方程，与混合物组分数量无关，因此该算法对于产物组分越多的裂解反应优势将会更加明显。此外，需要说明的是快速算法与全组分算法收敛性一致，在单步迭代计算速度显著提高的同时，保持了全组分算法的收敛性，并不会增加计算至流场收敛所需的迭代步数。

图5为快速算法与全组分算法计算的流场内温度、轴向速度(ux)以及正癸烷质量分数分布对比情况。不同算法计算得到的各参数在近壁面和流场内部均吻合很好，误差几乎可以忽略不计。

表2 不同算法的计算时间对比(计算模型见图1)

Table 2 Comparison of computation time of different algorithms (computation model is illustrated in Fig.1)

AlgorithmNo.ofspeciestransportequationsIterationnumberComputationtime/h17STE(DC)17200041.0117STE(LT)17200012.231STE(LT)120001.83

此外，快速算法计算得到的正癸烷质量分数和燃料平均温度与文献[13-14]中结果的对比情况分别如图6和图7所示，相对误差也均在±0.6%以内。结果表明快速算法在显著提高计算效率的同时保证了计算精度。

为了进一步考察快速算法的适用范围，针对压力为3.45～11.38 MPa，入口流量为0.3～0.7 mL/min的多种工况进行模拟，并与文献[14]中的数值和实验结果进行对比。首先比较了不同压力下流场内热物性沿流向变化情况，如图8所示。计算中入口流量为0.3 mL/min，最高壁温为823 K。各个压力下热物性均具有很高的计算精度，相对误差均在±5%以内。

图5 不同算法计算结果对比(p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K) Fig.5 Comparison of simulation results using different algorithms (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

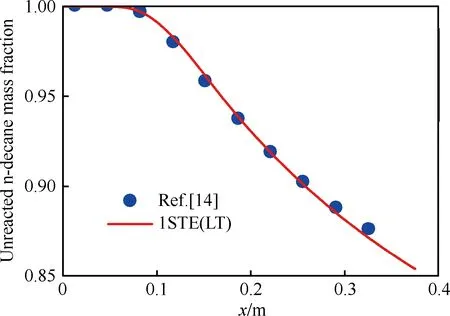
图6 轴线上正癸烷质量分数变化 (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K) Fig.6 Variation of n-decane mass fraction at tube axis (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

在不同压力和入口流量(0.5、0.7 mL/min)下，计算得到的出口处未裂解正癸烷质量分数与Ward等[14]实验测量结果对比情况如表3所示。计算时最高壁温为873 K。当裂解转换率小于25%时， 计算结果与实验相对误差在±1%以内；

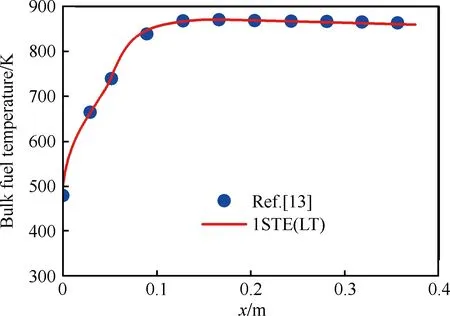
图7 燃料平均温度变化 (p0=3.45 MPa,m= 0.5 mL/min, Tw_max=873 K) Fig.7 Variation of bulk fuel temperature (p0=3.45 MPa, m=0.5 mL/min, Tw_max=873 K)

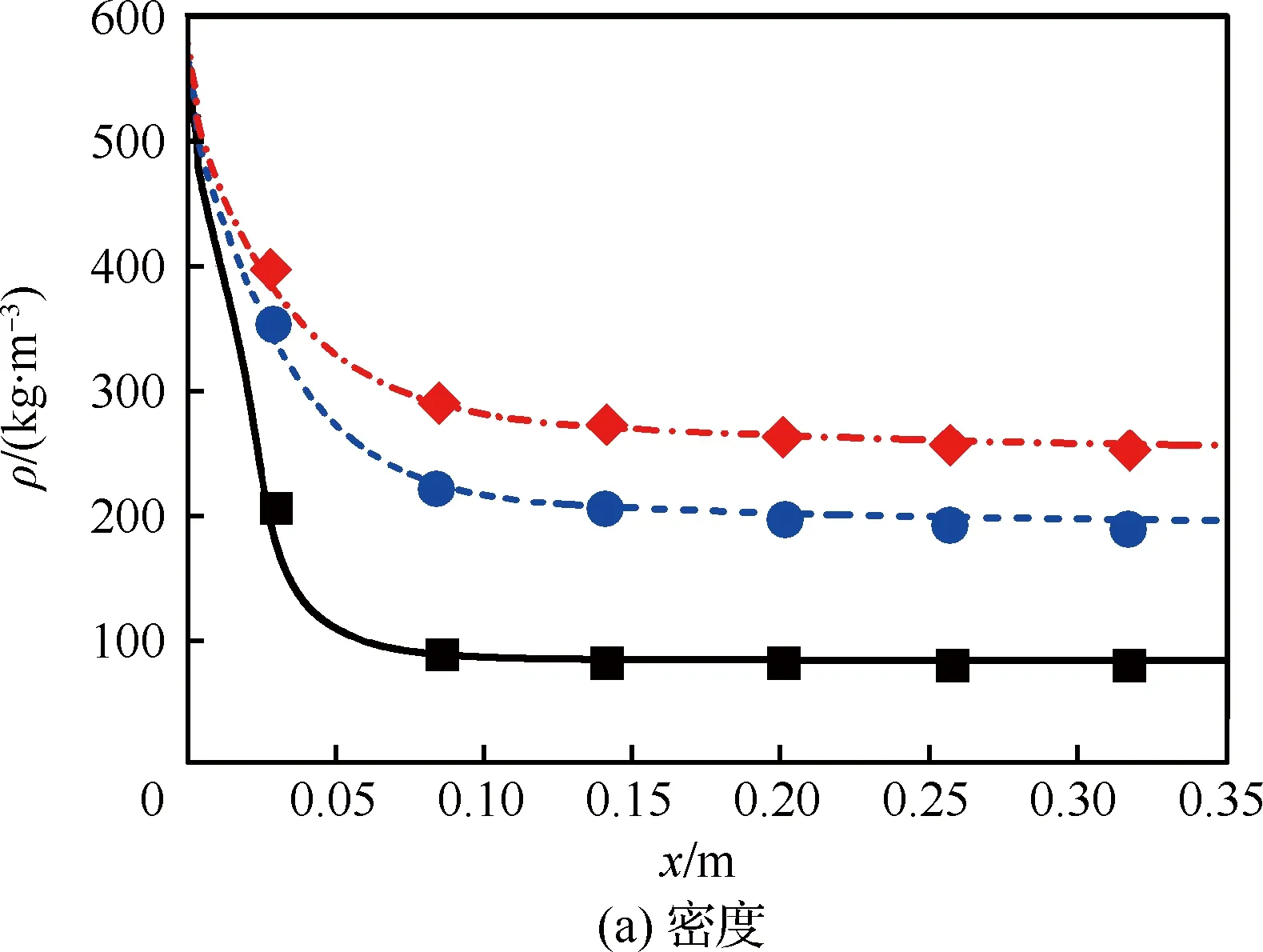
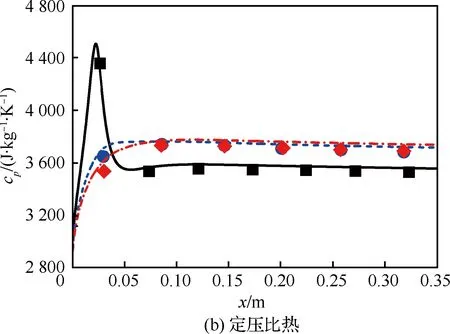
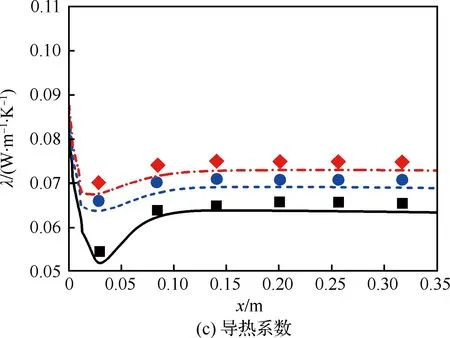
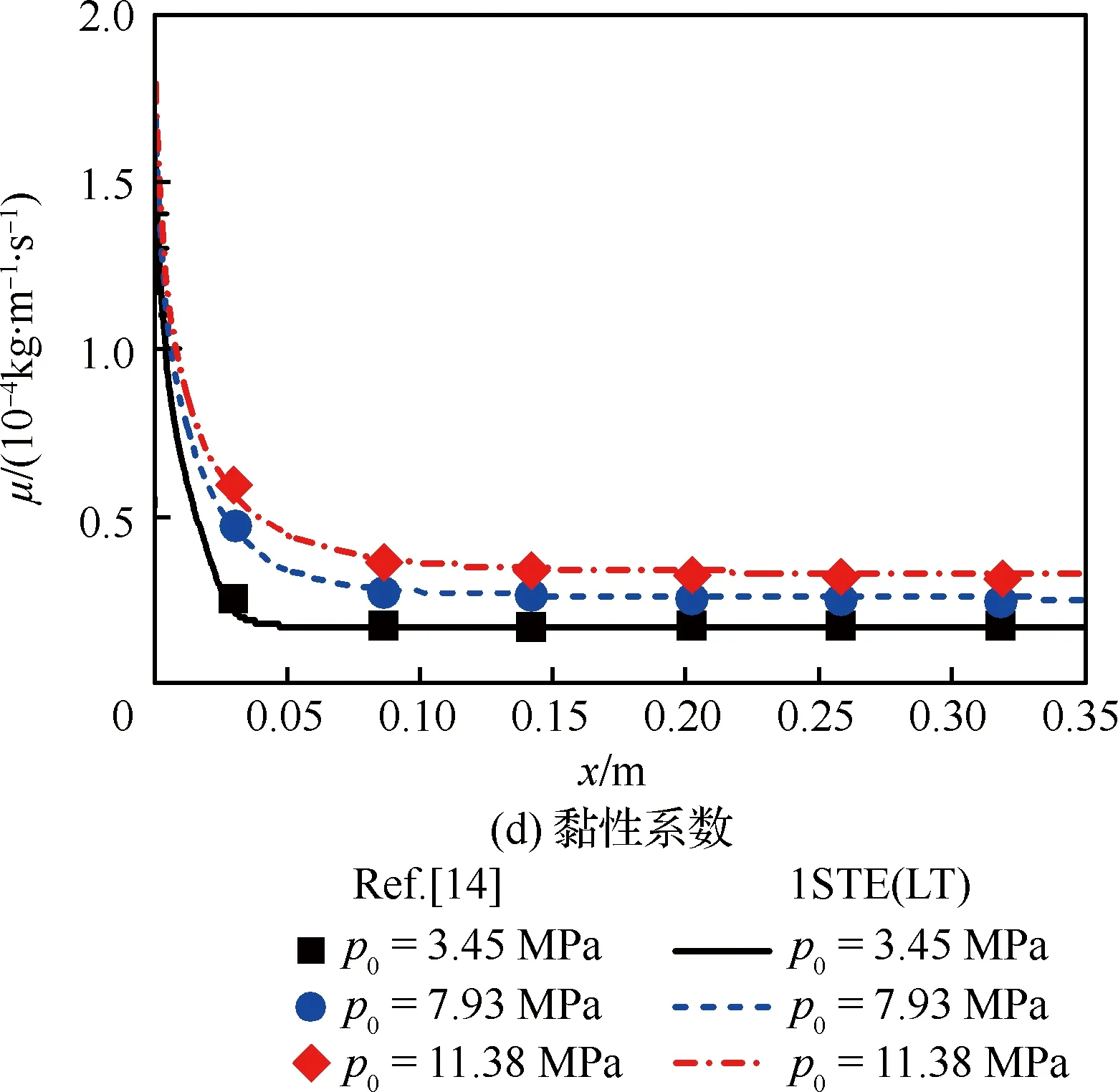
图8 不同压力下的热物性变化(m=0.3 mL/min, Tw_max=823 K) Fig.8 Variation of thermo-physical property under different pressures (m=0.3 mL/min, Tw_max=823 K)

表3 出口处未裂解正癸烷质量分数计算结果与实验对比

Table 3 Comparison of calculated and experimental results of unreacted n-decane mass fraction at outlet

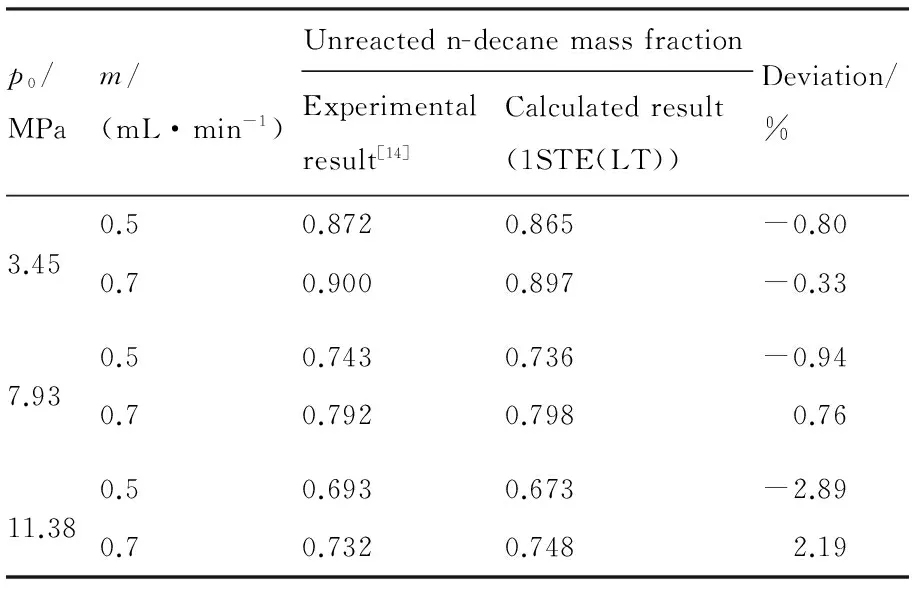
p0/MPam/(mL·min-1)Unreactedn-decanemassfractionExperimentalresult[14]Calculatedresult(1STE(LT))Deviation/%3.450.50.8720.865-0.800.70.9000.897-0.337.930.50.7430.736-0.940.70.7920.798 0.7611.380.50.6930.673-2.890.70.7320.748 2.19

当裂解转换率达到30%左右时，误差逐渐增大到±3%。这说明当裂解转化率大于25%时，开始发生轻微的二次裂解反应，而PPD机理无法考虑二次裂解的影响，因此误差有所增大。然而在裂解转化率达到30%时，二次裂解的影响带来的计算误差依然较小((3%以内)，因此在数值模拟中仍然可以近似采用PPD机理模拟裂解反应。综上所示，本文的快速算法适用于压力为3.45～11.38 MPa、裂解率为0～30%范围内的正癸烷裂解反应流动的模拟研究。

3.2 矩形截面冷却通道内传热分析

在工程应用中，准确预测超临界压力下碳氢燃料在非对称加热的矩形截面冷却通道中的裂解和传热特性对超燃冲压发动机主动冷却系统的设计非常重要。然而对于三维问题，为了准确捕捉近壁面流场参数的剧烈变化，所需计量网格量巨大。并且，对于含裂解反应的情况，由于混合物组分数量庞大，其计算量是目前开展详细数值模拟面临的主要困难。为了考察本文建立的快速算法对实际工程问题的适用性，本文进一步对三维矩形截面冷却通道非对称加热下的裂解反应流动进行模拟，并与已有的算法模拟结果进行比较。

冷却通道横截面尺寸为1.5 mm×1.5 mm，加热段总长300 mm，具体尺寸和计算坐标如图9所示。为了保证入口边界层的充分发展并减少出口边界条件对计算结果的影响，通道前后各取75 mm的绝热段。正癸烷入口质量流量为4 g/s，入口温度为700 K，上壁面为均匀热流qw=2.8 MW/m2，出口压力为4 MPa。

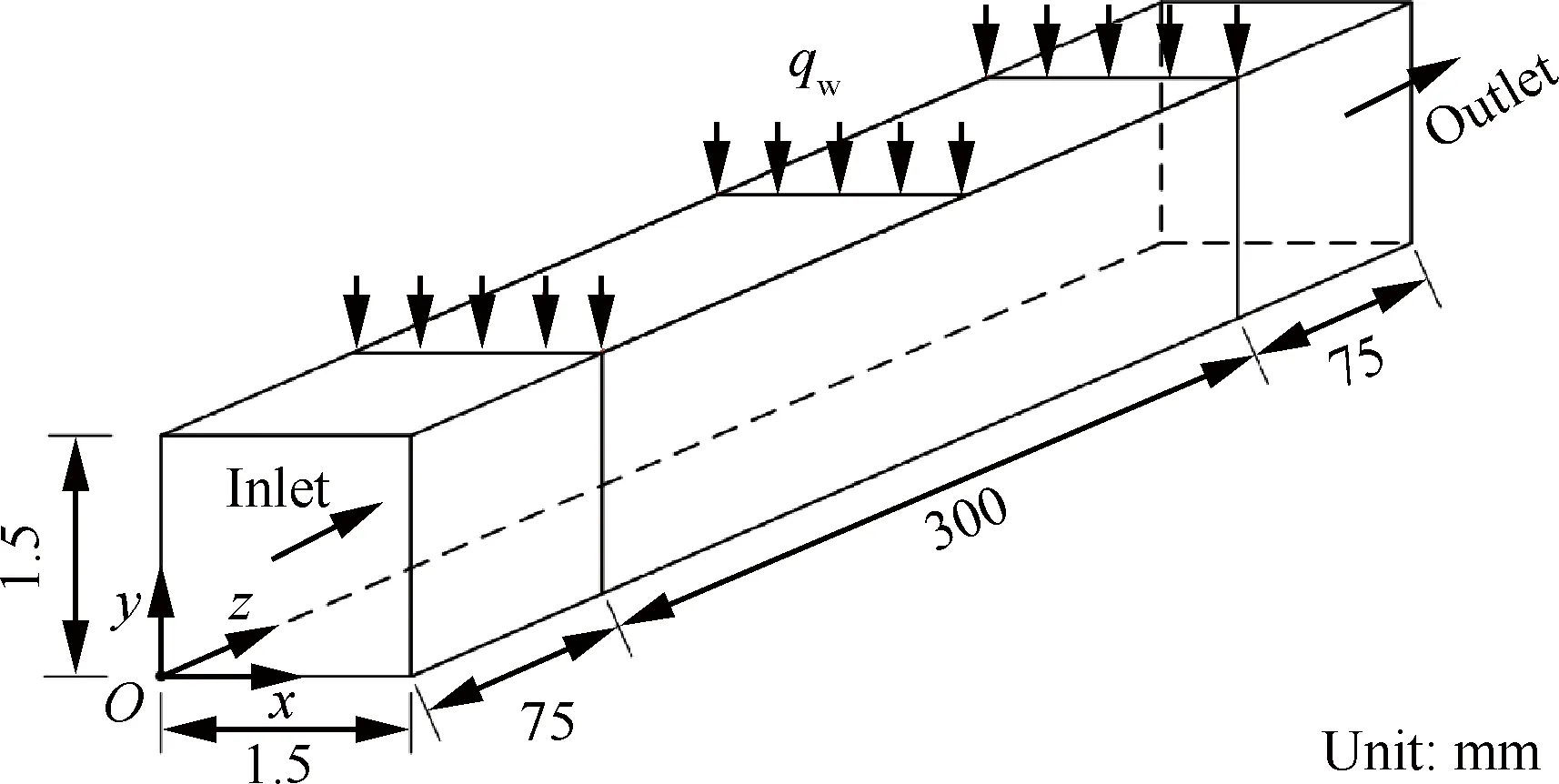
图9 三维矩形截面冷却通道示意图Fig.9 Schematic of 3D rectangular cooling channel

由于问题的对称性，选取模型的一半进行计算。在数值模拟之前，首先进行了网格独立性分析。对25×40×700、35×70×1 000、50×80×1 500这3套网格的计算结果进行了比较，发现35×70×1 000的网格已经满足网格无关性要求，当网格加密到50×80×1 500时，壁面温度变化在0.3%以内。综合考虑计算精度和效率，选择了35×70×1 000的网格进行计算。该算例在HP Z840工作站(处理器为Intel Xeon E5-2687W v4)上进行，各算例均采用40个核心并行计算。

表4为两种算法各迭代2 000步所用的时间对比。与前文中单核计算效率相近，快速算法将计算效率提高约20倍。

表4 不同算法的计算时间对比(计算模型见图9)

Table 4 Comparison of computation time of different algorithms (computation model is illustrated in Fig.9)

AlgorithmIterationnumberComputationtime/h17STE(DC)2000300.411STE(LT)200015.33

图10和图11给出了加热段各横截面(Oxy平面，坐标与图9对应)温度以及z向速度(uz)的分布。可以看出快速算法与全组分算法计算结果完全一致。由于热量从加热壁面不断传入，沿着流动方向，流体温度不断升高，密度下降，因而速度逐渐增大。由于热流集中在冷却通道的上壁面，因此速度最大的区域也逐渐向上壁面处移动。图10显示流体温度在上壁面与侧壁面的交界处(x=0)达到最大值，其主要原因是该处主流速度较小(见图11)，对流传热效果较差。

与圆管中的裂解和流动传热现象相比，流体在非对称加热的矩形冷却通道中的流动具有明显的三维特征。对于非对称加热矩形通道，上壁面热流集中使近壁面出现很高的温度梯度。温度越高裂解反应速率越快，而且近壁面流体流速低，滞留时间长，导致近壁面流体裂解转化率明显高于其他区域，形成很大的浓度梯度，尤其是在上壁面拐角处，如图12所示。组分浓度在近壁面的严重不均匀性使得扩散现象更加明显，其中裂解产物逐渐向通道内部扩散，同时未裂解正癸烷向近壁面扩散。

图10 不同横截面温度分布Fig.10 Temperature distribution at different cross-sections

图11 不同横截面速度分布Fig.11 Velocity distribution at different cross-sections

图12 不同横截面正癸烷质量分数分布Fig.12 n-decane mass fraction distribution at different cross-sections

图13 加热面不同位置壁面温度和正癸烷质量 分数变化 Fig.13 Variation of wall temperature and n-decane mass fraction at different positions of heated wall

图13为上壁面不同位置(x=0、5×10-5、7.5×10-4m，与图9所示坐标对应)的壁面温度和正癸烷质量分数沿流向变化情况。与全组分算法计算结果相比，快速算法的壁面温度相对误差在±0.1%以内，正癸烷质量分数相对误差在±0.5%以内。考虑到近壁面黏性底层内组分浓度梯度很大，且组分输运由分子扩散主导，因此分别假定两个常数形式的分子扩散系数(Di,m=4.0×10-7、7.0×10-7m2/s)进行模拟，用以研究黏性底层内分子扩散特性对组分浓度的影响。研究表明，在黏性底层组分浓度对分子扩散系数非常敏感，如图14所示。然而本文建立的分子扩散系数简化算法(式(9)，与图14中1STE(LT)对应)具有良好的计算精度，与直接计算分子扩散系数的全组分算法结果(17STE(DC))非常吻合。综上所述，该快速算法对于三维问题具有很好的适用性，可以精确捕捉流场的细微特征，具有工程应用价值。

图14 分子扩散系数对壁面正癸烷质量分数 分布的影响(x=0) Fig.14 Effect of molecular diffusion coefficient on n-decane mass fraction distribution at wall (x=0)

4 结 论

1) 本文建立的快速算法采用查表法计算裂解混合物的物性，并且将需要求解的组分输运方程由N-1个简化为1个。

2) 与全组分算法相比,快速算法计算效率提升了约20倍，同时还保留了全组分算法的计算精度。

3) 该算法适用于压力在3.45～11.38 MPa范围内的正癸烷轻度裂解与传热问题。当裂解率小于25%时，正癸烷质量分数的计算结果与实验数据相对误差在±1%以内；当裂解率达到30%左右时，误差在±3%以内。

4) 近壁面黏性底层内的裂解转化率和组分分布对分子扩散系数非常敏感，本文建立的分子扩散系数简化算法在不同压力和温度下均具有良好的计算精度。

5) 该算法能够快速、准确地模拟三维冷却通道内正癸烷裂解吸热与流动传热问题，具有良好的工程应用价值。

[1] POWELL O A, EDWARDS J T, NORRIS R B, et al. Development of hydrocarbon-fueled scramjet engines: The hypersonic technology (HyTech) program[J]. Journal of Propulsion and Power, 2001, 17(6): 1170-1176.

[2] BAO W, LI X, QIN J, et al. Efficient utilization of heat sink of hydrocarbon fuel for regeneratively cooled scramjet[J]. Applied Thermal Engineering, 2012, 33(1): 208-218.

[3] EDWARDS T. Cracking and deposition behavior of supercritical hydrocarbon aviation fuels[J]. Combustion Science & Technology, 2006, 178(1-3): 307-334.

[4] BAO W, ZHANG S, QIN J, et al. Numerical analysis of flowing cracked hydrocarbon fuel inside cooling channels in view of thermal management[J]. Energy, 2014, 67(4): 149-161.

[5] HUANG H, SOBEL D R, SPADACCINI L J. Endothermic heat-sink of hydrocarbon fuels for scramjet cooling: AIAA-2002-3871[R]. Reston, VA: AIAA, 2002.

[6] 俞刚， 范学军. 超声速燃烧与高超声速推进[J]. 力学进展, 2013, 43(5): 449-471.

YU G, FAN X J. Supersonic combustion and hypersonic propulsion[J]. Advances in Mechanics, 2013, 43(5): 449-471 (in Chinese).

[7] ZHONG Z, WANG Z, SUN M. Effects of fuel cracking on combustion characteristics of a supersonic model combustor[J]. Acta Astronautica, 2015, 110: 1-8.

[8] FAN X, YU G, LI J, et al. Combustion and ignition of thermally cracked kerosene in supersonic model combustors[J]. Journal of Propulsion and Power, 2007, 23(2): 317-324.

[9] ZHONG F Q, FAN X J, YU G, et al. Thermal cracking and heat sink capacity of aviation kerosene under super critical conditions[J]. Journal of Thermophysics & Heat Transfer, 2011, 25(6): 1226-1232.

[10] ZHONG F Q, FAN X J, YU G, et al. Thermal cracking of aviation kerosene for scramjet applications[J]. Science in China Series E: Technological Sciences, 2009, 52(9): 2644-2652.

[11] JIANG R, LIU G, ZHANG X. Thermal cracking of hydrocarbon aviation fuels in regenerative cooling microchannels[J]. Energy & Fuels, 2013, 27(5): 2563-2577.

[12] STEWART J, BREZINSKY K, GLASSMAN I. Supercritical pyrolysis of decalin, tetralin, and n-decane at 700-800K: Product distribution and reaction mechanism[J]. Combustion Science & Technology, 1998, 136(1-6): 373-390.

[13] WARD T, ZABARNICK S, ERVIN J, et al. Simulations of flowing mildly-cracked normal alkanes incorporating proportional product distributions[J]. Journal of Propulsion and Power, 2004, 20(3): 394-402.

[14] WARD T A, ERVIN J S, ZABARNICK S, et al. Pressure effects on flowing mildly-cracked n-decane[J]. Journal of Propulsion and Power, 2005, 21(2): 344-355.

[15] ZHU Y, LIU B, JIANG P. Experimental and numerical investigations on n-decane thermal cracking at supercritical pressures in a vertical tube[J]. Energy & Fuels, 2013, 28(1): 466-474.

[16] XU K, MENG H. Analyses of surrogate models for calculating thermophysical properties of aviation kerosene RP-3 at supercritical pressures[J]. Science in China Series E: Technological Sciences, 2015, 58(3): 510-518.

[17] 阮波，孟华. 碳氢燃料裂解吸热反应及超临界传热现象数值模型的构建与验证[J]. 航空学报, 2011, 32(12): 2220-2226.

RUAN B, MENG H. Numerical model development and validation for hydrocarbon fuel supercritical heat transfer with endothermic pyrolysis[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2220-2226 (in Chinese).

[18] ZHANG S, FENG Y, JIANG Y, et al. Thermal behavior in the cracking reaction zone of scramjet cooling channels at different channel aspect ratios[J]. Acta Astronautica, 2016, 127: 41-56.

[19] FENG Y, JIANG Y, LI X, et al. Numerical study on the influences of heat and mass transfers on the pyrolysis of hydrocarbon fuel in mini-channel[J]. Applied Thermal Engineering, 2017, 119: 650-658.

[20] 刘志琦. 超燃冲压发动机主动冷却通道内的超临界流动与传热过程数值模拟[D]. 长沙： 国防科学技术大学, 2015: 18-26.

LIU Z Q. Numerical simulation of flow and heat transfer in cooling channels of active cooled scramjet engines[D]. Changsha: National University of Defense Technology, 2015: 18-26 (in Chinese).

[21] 程泽源， 朱剑琴. 低裂解度正癸烷物性快速计算方法[J]. 推进技术, 2016, 37(8): 1586-1593.

CHENG Z Y, ZHU J Q. Fast calculation method on physical properties in mild cracking of decane[J]. Journal of Propulsion Technology, 2016, 37(8): 1586-1593 (in Chinese).

[22] RUAN B, MENG H, YANG V. Simplification of pyrolytic reaction mechanism and turbulent heat transfer of n-decane at supercritical pressures[J]. International Journal of Heat and Mass Transfer, 2014, 69(2): 455-463.

[23] ELY J F, HANLEY H. Prediction of transport properties: 1. Viscosity of fluids and mixtures[J]. Industrial & Engineering Chemistry Fundamentals, 1981, 20(4): 323-332.

[24] ELY J F, HANLEY H. Prediction of transport properties: 2. Thermal conductivity of pure fluids and mixtures[J]. Industrial & Engineering Chemistry Fundamentals, 1983, 22(1): 90-97.

[25] MENG H, YANG V. A unified treatment of general fluid thermodynamics and its application to a preconditioning scheme[J]. Journal of Computational Physics, 2003, 189(1): 277-304.

[26] MENG H, HSIAO G C, YANG V, et al. Transport and dynamics of liquid oxygen droplets in supercritical hydrogen streams[J]. Journal of Fluid Mechanics, 2005, 527: 115-139.

[27] 阮波. 超临界压力下正癸烷裂解吸热和对流传热现象的数值模拟研究[D]. 杭州： 浙江大学, 2013: 40-61.

RUAN B. Numerical studies of convective heat transfer of n-decane with endothermic pyrolytic reaction at supercritical pressures[D]. Hangzhou: Zhejiang University, 2013:40-61 (in Chinese).

[28] STEWART J F. Supercritical pyrolysis of the endothermic fuels methylcyclohexane, decalin, and tetralin[J]. Dissertation Abstracts International, 1999, 60(9): 4852-5119.

附录A：

已知方程组

(A1)

假设Sb=θSa在整个求解域中恒成立，求证：方程组(A1)的解满足Yb=θYa。

证明：根据上述偏微分方程和定解条件可知式(A1)为定解问题，解是唯一的。

对其中任意产物组分a和b，若Sb=θSa,则有

(A2)

根据微分算子性质有A(θYa)=θA(Ya)=θSa,再根据定解条件可得：

(A3)

即Yb和θYa分别满足式(A2)和式(A3)中的偏微分方程和定解条件。由于式(A2)和式(A3)中的方程和定解条件完全相同，根据解的唯一性可知Yb=θYa。

证明完毕。