不同供电方式下永磁同步电动机铁耗计算与分析

魏静微，于 晓，黄全全

(哈尔滨理工大学，哈尔滨 150080)

0 引 言

当工频电源直接带大惯量负载时，电机起动电流很大，会导致电机寿命大大缩短。传统方法采用变频器和三相感应电动机带动大惯量负载，由于三相感应电动机起动转矩低、效率和功率密度不高，正逐渐被体积更小、结构简单、效率和功率密度更高、经济运行范围宽的永磁电动机取代[1-2]。

目前，国外对逆变电源供电下永磁同步电动机的研究比较深刻，利用时步有限元法建立电机的物理模型，研究PWM供电下对电机铁耗的影响等。国内关于变频器供电下的铁耗分析计算也较多，研究逆变器的调制比和载波比对铁耗的影响等[3]。但精确计算铁耗仍是国内外学者亟待解决的问题，计算得到的电机铁耗与实验测得的电机铁耗仍有较大的误差。计算损耗值过低或过高都会对电机的性能分析产生一定的负面影响[1,4]。

本文首先对永磁同步电动机定子铁耗的计算模型进行了研究，该模型将铁耗分为3项进行计算，最后将这3项铁耗叠加为电机损耗，其中包括磁滞损耗、涡流损耗、附加损耗。然后利用Ansoft/Maxwell软件，采用时步有限元法，画出各点径向、切向磁密波形图并进行傅里叶分解，进而求出各点的定子损耗，并与仿真结果进行对比。另外，通过控制变频器的不同参数来观察定子铁心损耗的变化规律。

1 计算模型及电机参数

1.1 计算模型

依据Bertottti提出的铁耗分离模型，铁耗分为磁滞损耗ph、经典涡流损耗pc和异常涡流损耗pexc。即：

pFe=ph+pc+pexc

(1)

磁滞损耗是电机通电后，电机铁心置于交变的磁场中被反复磁化，铁磁材料内部磁畴相互不停的摩擦产生的损耗；经典涡流损耗是由于铁心导电，在交流电源作用下，通过铁心中的磁通随时间交变，依据电磁感应定律，铁心中将产生涡流，由此涡流产生的损耗；异常涡流损耗又称附加损耗，其产生认为与磁畴结构有关，一般很小而被忽略[5-6]。

当磁密为理想正弦变化时，Bt=Bmsin(2πft)，定子铁心损耗按下式计算：

pFe=kh(fBm)χ+ke(fBm)β+kexc(fBm)α

(2)

式中：f为交变磁场的频率；Bm为铁心磁密幅值；kh,ke,kexc分别为磁滞损耗系数、 涡流损耗系数和附加损耗系数，可根据硅钢片损耗曲线拟合得到；χ，β，α分别为磁滞损耗、涡流损耗、附加损耗的计算参数[7-8]。

当变频电源供电时，输入电源谐波含量较大,导致磁密谐波含量较大，磁滞损耗按下式计算：

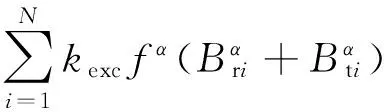
(3)

式中：Bri，Bti分别为铁心径向和切向磁密的第i次谐波分量幅值[9]。 先求解铁心各部位磁密的径向和切向分量，并将铁心径向和切向磁密做傅里叶分解。

从式(3)可以看出，铁耗主要取决于铁心材料的各损耗系数、频率和磁密，当电机频率一定时，其对应各损耗系数也可通过拟合确定，此时只需求出磁密便可求得电机铁耗。根据型号DW465-50的硅钢片， 可以求得式(3)，kh,ke,kexc可分别取0.0281，1.919×10-4，7.47×10-7； 默认χ，β均取 2，α取 1.5。

1.2 电机参数

自起动永磁同步电动机是转子上安装有鼠笼条的永磁同步电动机，与其他永磁电动机相比，它具备自起动能力。电机起动时，定子电流产生的同步旋转磁场和转子鼠笼条相互作用实现自起动。当直接带大惯量负载时，电机起动电流过大会导致电机寿命缩短，因此需要用变频器和永磁同步电动机带动大惯量负载。本文选用的永磁同步电动机部分参数如表1所示[10]。

表1 电机的基本参数

2 正弦供电下的铁耗计算

稳态运行时永磁同步电动机转子转速达到同步转速，此时空间旋转磁场与转子保持相对静止，转子铁心基本没有铁耗产生，因此在计算永磁同步电动机铁耗时，主要是对定子铁耗的分析。理论上，在计算整个定子铁耗时，需要掌握定子铁心各部位磁密分布及变化规律。然而，定子铁心各点磁密变化方式、磁密幅值都是不同的，求取整个定子各点磁密是不可能办到的。

研究认为，定子齿部与轭部可以取中间点的磁密等效为整个齿、轭部磁密[3,11]。因此本文采用时步有限元的思想，将定子铁心分为4个典型的区域，并分别求取各个区域的铁耗，最后相加求出定子总铁耗。定子铁耗等效图如图1所示。将定子铁心划分为齿顶、齿中、齿尾、轭部，并分别取其中点a,b,c,d磁密来等效其对应整个区域的磁密[1,7,12]。

图1 定子铁耗等效图

2.1 各点磁密空间分布及径向、切向磁密的波形图

正弦空载稳态运行时，针对定子铁心的4个典型位置点，一个周期内各点的径向、切向磁密曲线及磁密矢量轨迹如图2所示。

(a)a点径切磁密及磁矢量轨迹

(b)b点径切磁密及磁矢量轨迹

(c)c点径切磁密及磁矢量轨迹

(d)d点径切磁密及磁矢量轨迹

图2定子各点磁密波形及磁矢量轨迹

图2中显示a，b，c，d点径向与切向磁场基本上都是同向或反向，假设图中磁矢量轨迹分布图的坐标取值范围相同，磁矢量轨迹会呈直线或椭圆分布，说明这些区域受磁场的影响比较大。

2.2 各点径切磁密的傅里叶分解

在计算电机铁耗时，由于磁密存在谐波，现将定子各点磁密的径向、切向分量分别做傅里叶分解，再将各次谐波幅值代入公式，从而计算出正弦电源空载稳态时的定子铁耗。各点磁密傅里叶分解如图3所示。

(a)a点径向及切向磁密

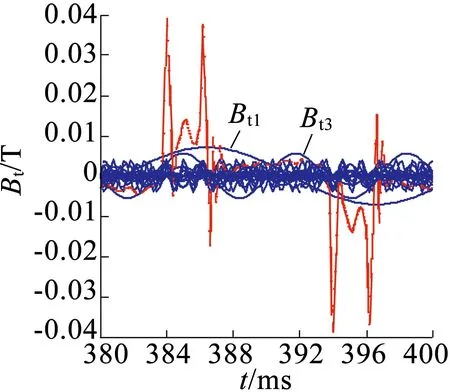
(b)b点径向及切向磁密

(c)c点径向及切向磁密

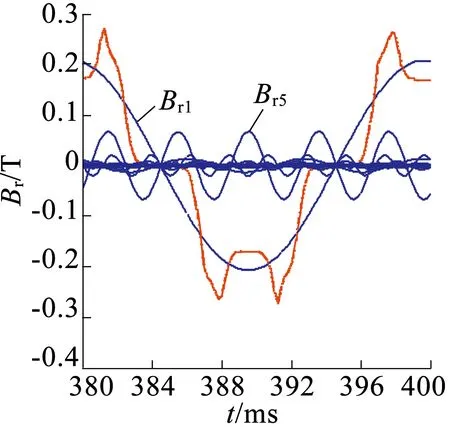
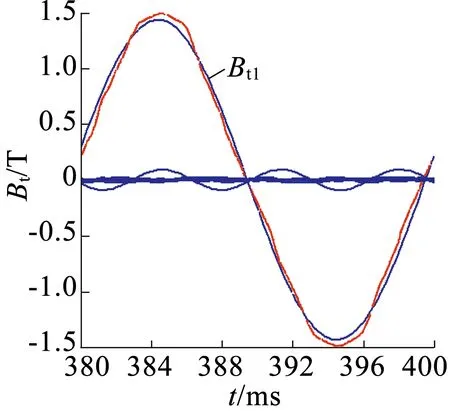
(d)d点径向及切向磁密

图3定子各点磁密傅里叶分解波形

图3能直观地反映各点径向和切向磁密及其谐波，现对其各次谐波幅值提取,如表2所示。

表2 定子各点磁密傅里叶分解谐波幅值(T)

将各次谐波幅值代入式(3)，计算出工频状态下电机定子损耗，结果如表3所示。

表3 正弦空载稳态时铁耗*

*：表中数据是电机铁耗公式计算结果乘以对应区域铁的总质量后所得[13]。

定子各点铁心损耗的占比图如图4所示。齿轭的体积最大，所占的总损耗最高，为66.00%；其次是齿中、齿尾，分别占22.30%，8.50%；齿顶体积最小，所占的总损耗最低，为3.20%。

图4 定子各点铁耗占比图

利用软件Ansoft/Maxwell，通过RMxprt将设计的11kW自起动永磁同步电动机参数设置后，得到的定子铁耗等参数，如图5所示。由图5得出，定子铁耗参数为114.736W。

图5 RMxprt参数图

二维有限元铁耗曲线图如图6所示。从图6中可以看出，350～400ms稳态时的铁耗值为89.94W。

图6 二维有限元铁耗曲线图

铁耗误差如表4所示。用铁耗公式计算出的定子铁耗为93.59W，由图5可知，RMxprt仿真永磁同步电机的定子铁耗为114.38W，与铁耗计算值相比，定子铁耗误差为22.2%，显然误差不在合理范围内。Ansoft计算电机铁耗时，通常有场和路两种计算方法，基本铁耗是由主磁场在铁心内发生变化时产生的，RMxprt为路的计算，二维时步有限元是电磁场模拟仿真，比如求损耗、磁密、转矩等，所以相比路的计算，场的计算更准确，因此采用二维时步有限元计算方法时，如表4所示，定子铁心损耗为89.94W，与铁耗公式计算值相比，误差为3.9%，误差在合理范围内，说明计算方法正确。

表4 损耗误差表

3 逆变电源对定子铁耗的影响

3.1 变频电路

在模拟变频器供电时，只需要搭建变频器中的逆变器电路模块，即直流电逆变成交流电对电机供电，从而实现变频电源供电对电机运行的分析。首先通过RMxprt可求解电机定子绕组参数：LA=0.463 389mH，RA=0.391 695Ω；其次，用Ansoft自带的CircuitEditor电路编辑模块搭建电机外接逆变电路，如图7所示，定子绕组为Y接。LPA，LPB，LPC为定子三相绕组；RA,RB,RC为定子三相绕组各相电阻；LA，LB，LC为三相绕组各相电感；DC为直流侧电压。S1～S6为控制开关；D1～D6为续流二极管[14]。

图7 电机逆变电源电路

3.2 调制比和载波比对定子铁耗的影响

在分析调制比对永磁同步电动机铁耗的影响时，保持电源频率为50Hz,载波比N=40；调节直流母线电压，使输入基波相电压保持220V不变，此时计算不同调制比下电机定子铁耗，如表5和图8所示。由表5可见，变频电源(M=0.8，N=40)比正弦电源供电时铁耗增加了17.75%，且调制比越大，电机铁耗越小。这是因为电机稳态运行时，变压器调制比越大，其直流母线电压越小，谐波幅值减小，电机铁耗降低。

表5 不同调制比时定子铁耗

图8 调制比对定子铁耗影响

在分析载波比对电机损耗的影响时，保持电源频率为50 Hz,调制比M=0.9，直流母线电压不变，使输入基波相电压保持220 V不变，此时调节开关频率，使载波比N从10增大到80，并计算电机定子铁耗，结果如表6和图9所示。由表6可见，载波比越大，电机铁耗越小。因为当开关频率越高时，采样点越密集，逆变器输出电压谐波含量就越小，从而使磁密谐波含量降低，损耗就越小[4,15]。

表6 不同载波比时电机铁耗

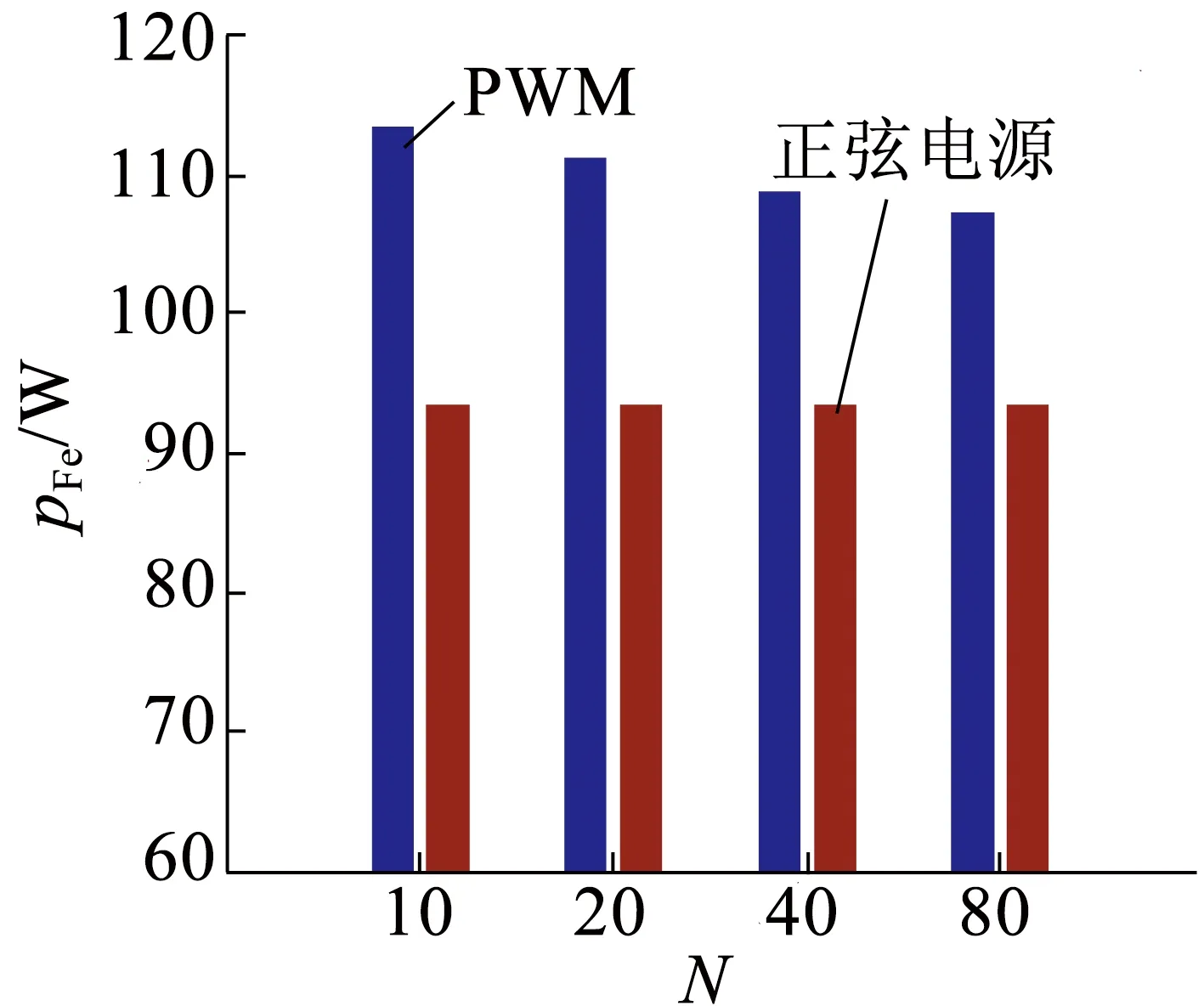
图9 载波比对定子铁耗影响

通过研究调制比和载波比变化对铁耗的影响发现，在使用变频电源供电时，应采用较高的调制比和载波比以减小电机铁耗。如果考虑变频器的损耗，载波比不能设置的过大，否则载波比越大，开关频率就越大，变频器损耗也会越大。

4 结 语

本文主要研究了正弦供电下定子铁耗的计算，并且研究了变频电源的调制比和载波比对11kW永磁同步电动机的定子铁耗影响，以及对定子铁心不同区域的磁密进行傅里叶分解研究。通过本文研究，可得出如下结论：

1) 定子铁心损耗分为磁滞损耗，涡流损耗和附加损耗，将定子铁心划为4个典型区域，其中齿轭的总损耗最高，占一半以上，其次是齿中、齿尾，齿顶的损耗最少。

2) 基本铁耗是主磁场在铁心内发生变化时产生的，RMxprt是路的计算，所以公式计算定子铁心损耗所得结果与RMxprt仿真结果相比，误差较大。Ansoft计算电机损耗有场和路两种计算方法，相对路的计算，场的计算更加准确，而二维时步有限元是电磁场模拟仿真，所以与公式计算相比，误差在合理范围内。

3) 调制比和载波比对永磁同步电动机定子铁耗产生影响。当调制比一定时，随着载波比的增大，

定子铁心损耗减少。当载波比一定时，随着调制比的增大，定子铁心损耗也减少。因此变频电源供电时应采用较高的调制比和载波比以减小铁耗，但载波比和调制比设置过高会使变频器损耗增加。所以综合考虑，变频电源给电机供电时应采用适当的调制比和载波比。

[1] 刘书齐．SPWM变频器供电下永磁同步电动机的铁耗分析[D]．哈尔滨：哈尔滨理工大学，2015.

[2] 郭培.异步起动永磁同步电机的研究[D].杭州：浙江大学，2013.

[3] 佟文明，朱晓锋，贾建国．时间谐波对永磁同步电机损耗的影响规律[J]．电工技术学报，2015，30(6)：61-68．

[4] 李跃龙．PWM逆变器供电下异步电动机的铁耗分析[D]．哈尔滨：哈尔滨理工大学，2014.

[5] 沈启平．变频器供电下定子磁动势引起的永磁同步电机转子损耗分析[J]．电工技术学报，2016，31(4)：52-57．

[6] 王朋，邹海荣，张周云，等．电动汽车用永磁同步电机铁耗计算[J]．微特电机，2015，43(7)：26-29．

[7] 于明湖，张玉秋，张波．永磁同步发电机铁耗计算分析[J]，微特电机，2015，43(7)：21-25.

[8] 李宏涛，戈宝军．变频器驱动下异步电机铁心损耗的研究[J]．大电机技术，2013(1)：4-10．

[9] 张洪亮，邹继斌．考虑旋转磁通的PMSM 铁心损耗数值计算[J].电机与控制学报，2007,11(4) : 340-344.

[10] 陈世坤．电机设计[M]．北京：机械工业出版社，2012.

[11] 赵海森，罗应立，刘晓芳，等．异步电机空载铁耗分布的时步有限元分析[J]．中国电机工程学报,2010，30(30):99-106．

[12] TONG W,WU S,SUN J,et al．Iron Loss Analysis of Permanent Magnet Synchronous Motor with an Amorphous Stator Core[C]//Vehicle Power and Propulsion Conference.IEEE,2016:1-6．

[13] 安忠良，徐作为，兰玉华，等．异步起动永磁同步电机铁耗分析及计算[J]．微电机,2016，49(5)：6-10．

[14] 王兆宇．施耐德电气变频器原理与应用[M]．北京：机械工业出版社，2009．

[15] 韩力，谢李丹．变频器参数对永磁同步发电机定子损耗的影响[J]．电机与控制学报，2010，14(12)：76-80．