基于多目标优化的电机驱动伺服转台切换模型
叶 超, 郭绪猛, 张 倩, 王群京
(1.中国电子科技集团公司第三十八研究所,合肥 230088;2.安徽大学,合肥 230601)
0 引 言
电机驱动伺服转台在以中等速度平稳运行时,基本呈现线性输入输出关系。但当系统处于低速运行状态特别是换相时,非线性因素的作用十分明显。常见的非线性因素包括摩擦、齿隙、电机力矩波动、机械结构形变等;严重影响电机驱动伺服转台的整体性能,尤其是低速性能,容易造成波形畸变、极限环、爬行等现象;严重影响转台的工作效果。因此建立可以体现电机及转台整体系统在不同工作速度下的精确数学模型,尤其在低速区的非线性模型,是实现转台精确跟踪及控制、提高复杂环境下工作性能的基础。
本文针对电机驱动伺服转台运行过程中出现的参数和模型结构摄动问题,对转台在不同工况下的输入输出关系展开研究。在低速区应用非线性模型对系统输入输出关系进行描述;对平稳工作的工况,保留结构简单的线性数学模型。构建以各子系统模型输出误差最小为优化目标,以各模态之间平滑切换为有约束多目标优化问题(以下简称CMOP),获得电机驱动伺服转台的切换模型参数。实验结果表明,该启发式的多目标优化方法可获得良好的参数辨识结果,所得切换系统模型可以较好的逼近实际系统,为电机驱动伺服转台的高精度控制器设计提供基础。
1 伺服转台及辨识实验
以某型号无人机机载雷达的伺服转台为研究对象,以力矩电机驱动电压为输入,以该转台的俯仰角速度为输出。对该单输入单输出系统,设计并实施基于切换模型的系统辨识实验。对辨识实验所得数据按照工况分析获得的数学条件进行划分。首先,考虑正向运行和反向运行的非线性作用因素不同,以伺服转台的输出速度作为状态变量,并以此作为切换条件。其次,低速区摩擦非线性及力矩波动等扰动因素作用明显,因此以速度绝对值作为工况划分的另一指标。为不失一般性,在正转v(k)≥0和反转v(k)<0时,以两个线性子系统描述平稳运行的工作状态,以非线性子系统描述低速区系统状况,在各系统间平稳切换,构成多模型切换系统模型。
辨识实验所得数据的获得要充分考虑伺服转台各种工作状态,输入信号覆盖常见输入信号频率范围,幅值不应超过机械结构限制范围,数据量应满足提供关于系统的信息的要求。实验中选取调频正弦频扫Chrip信号及正/负阶跃信号。其中Chrip信号频率由1 Hz增加至10 Hz,作为辨识信号;阶跃信号则主要作为检验模型准确性的验证信号。采样周期为9.1ms,控制信号输入范围为u(k)∈[-7.4V,7.4V],一组输入输出信号如图1所示。由图1可以明显看出输出角速度在过零点附近波形发生明显的畸变,说明系统的输入输出特性在这个区域内与正常工况下有所不同,验证了切换系统应用的实际基础。
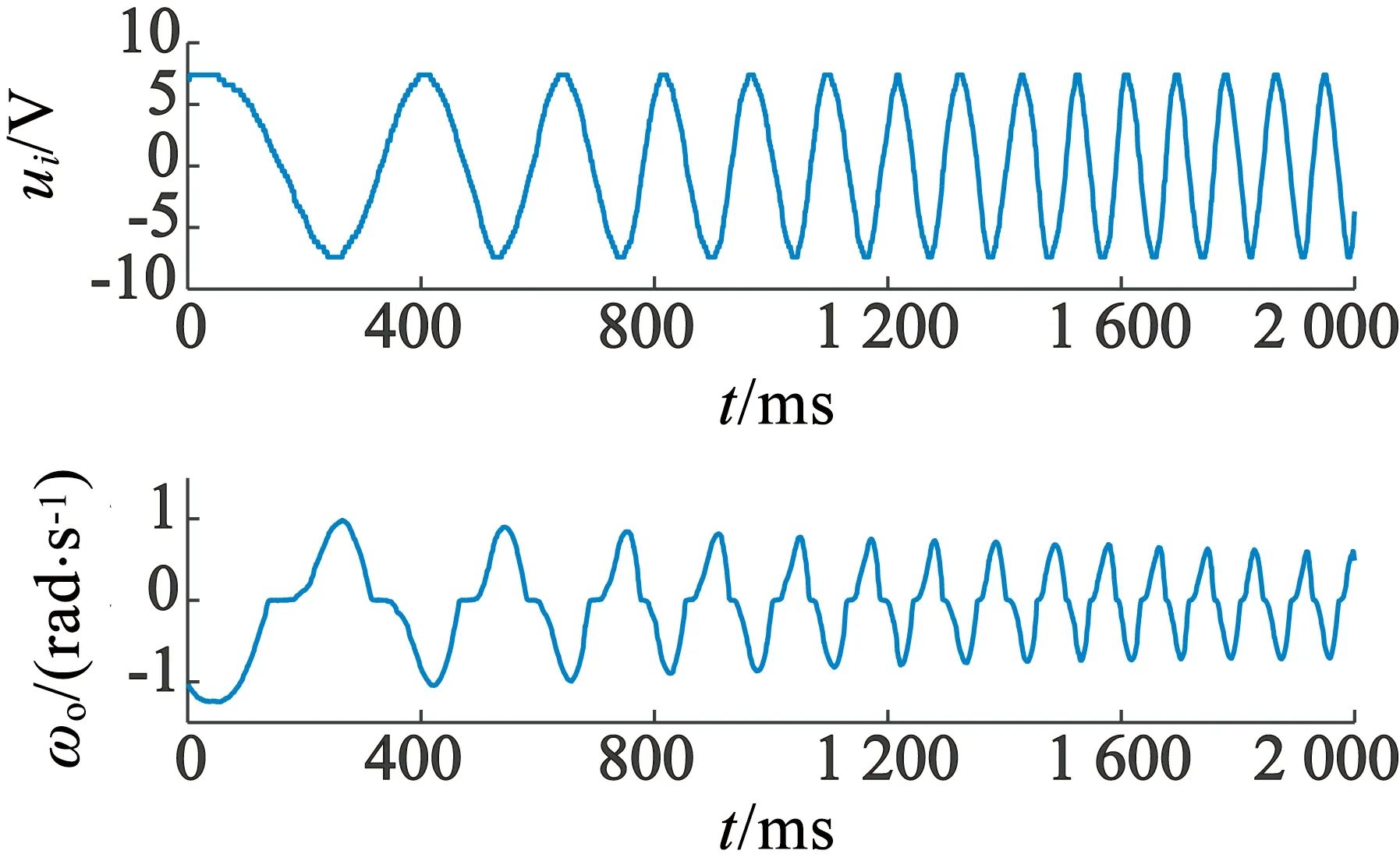
图1 正弦频扫Chrip信号下系统输入输出曲线
2 切换系统模型
切换系统的模型形式多样,有4元组模型或由多组子系统及切换条件共同构成。针对上述机载雷达的俯仰角速度控制系统,根据输出角速度的正负及阈值,将连续系统划分为M个模态,采用广义Hammerstein模型对每个模态的输入输出关系进行精确描述[6]。Hammerstein模型有非线性静态模块和线性动态模块串联而成[7]。在过零点附近建立Hammerstein结构非线性模型,在中速运行时则选用线性模型进行拟合。系统模型结构示意图如图2所示,其中Fσ[u(k)]为Hammerstein模型的非线性静态模块,在线性子系统中退化为1。
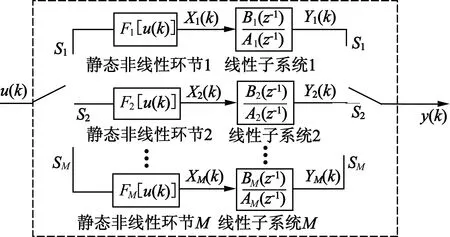
图2 M模态广义Hammerstein切换系统模型
为不失一般性,取M=4,即存在4个模态Sσ,σ=1,2,3,4。各子系统的广义Hammerstein数学模型如下式:
(1)
式(1)中,aσ1,aσ2,aσ3和bσ0,bσ1为离散线性子系统的差分方程系数;Fσ[u(k)]为非线性子系统,目前以高阶方程形式表示,取阶数为2,Fσ[u(k)]=fσ1u(k)+fσ2u2(k),fσ1,fσ2均为建模的非线性子系统模型系数。对线性子系统的模态下,Hammerstein模型退化为线性受控自回归模型,非线性部分参数为零,切换条件由输出变量驱动。S2与S4分别表示正、反向平稳运行,系统模型为线性系统,fσ2=0。S1表示正向低速运行的动作状态;S3则表示反向的非线性工况模态。
(2)
式中:Sσ表示第σ个模态;ε1,ε2为切换条件的阈值。Δy(k)=y(k)-y(k-1)为输出变量的增量,γ1,γ2是加速或减速的运行状态,由不同伺服系统的结构和元器件参数及运行状态要求决定,可通过机理分析和试验确定。ε1,ε2由天线伺服转台的机械结构决定,经前期的研究基础和实验对比,取:
(3)
(4)
式中:ypos_max为正向最大转速;yneg_min则为反向最小转速。
3 CMOP构建及求解
3.1 CMOP构建
首先建立4个相对独立的优化目标minJσ(θ),σ=1,2,3,4,表征在每一个模态下各子系统模型对系统输入输出关系描述的准确性:
但是。他知道什么是爱。她想,连她自己都未曾知道,什么是爱,什么是真正的爱,什么是可以长久和坚定的爱,什么是充满温柔和忍耐的爱,什么是不会变化不会消减不会失去的爱。呵。她从来没有见到过。她只见到过人为爱所迷惘,所翻腾,所覆盖,所毁灭,所撕裂,所粉碎。世间所谓的爱,最终都不过是人们各自的失望。所有人,一定还未曾得到爱的真谛。
(5)
式中:Fσ(y,u)为第σ个子模型的预测输出;Yσ为该模态下伺服转台的实际输出。
用切换系统模型描述机电伺服转台的主要目的是为多工况下的切换控制建立数学基础,在多个模态的切换时,要求模型输出没有波动或摄动较小,依此建立约束条件。假设在辨识实验周期内总切换次数为I,在任意切换时刻ki,i=1,2,…,I,由第σ个模态切换至σ+δ模态,应满足:
yσ(ki)=yσ+δ(ki)
(6)
式中:yσ+δ(ki)和yσ(ki)分别表示ki切换时刻σ+δ和σ子模型输出,M=4,δ=1,-1,3。
CMOP构建:
minJ=J(θ)=[J1(θ),J2(θ),J3(θ),J4(θ)]=
(7)
(8)
以加权系数1构成单一的目标函数,再将约束条件h(ki)=0,i=1,2,…,I以加权系数λi纳入到该目标函数中:
L(θT,λ1,…,λI)=J1(θ)+J2(θ)+J3(θ)+
(9)
应用Lagrange乘子实现线性加权,Ji(θ)表征不同工况下子系统模型的拟合程度,取相同权值。将各个模型之间的平稳切换作为约束,再利用极大极小法将该约束纳入评价函数中,最后形成的单目标问题适应度函数如下:
(10)
3.2 CMOP求解
为提高寻优能力,对传统PSO算法有较多改进[8-11],本文应用多目标粒子群优化算法(以下简称MOPSO)求解所构建的多目标优化问题[8,10],伪代码如图3所示。
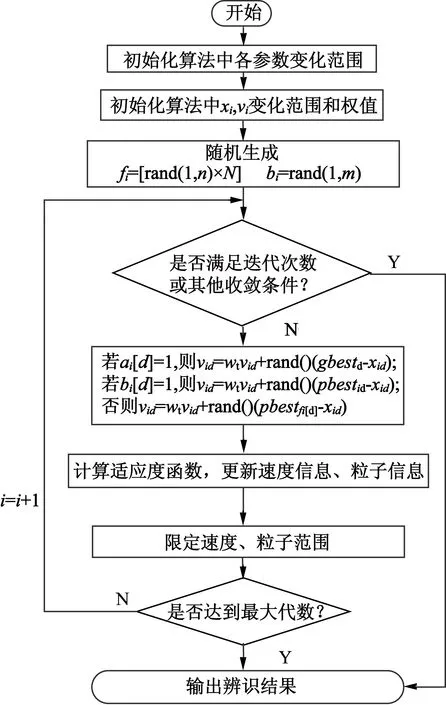
图3 MOPSO流程图
4 参数辨识结果及对比
运行50次程序,取出现概率最高的输出值作为辨识所得参数,所得切换系统模型的参数辨识结果如表1所示。采用正向阶跃信号,进行交叉验证。在正向阶跃信号作用下,模型输出与实际系统现场记录数据对比如图4所示。对角度θr的实际值与辨识输出值对比曲线如图5所示。由图5可见,建立的切换系统模型可在过零、正向运行、反转等状态下,拟合电机驱动伺服转台的输入输出情况,对角度和角速度进行计算。
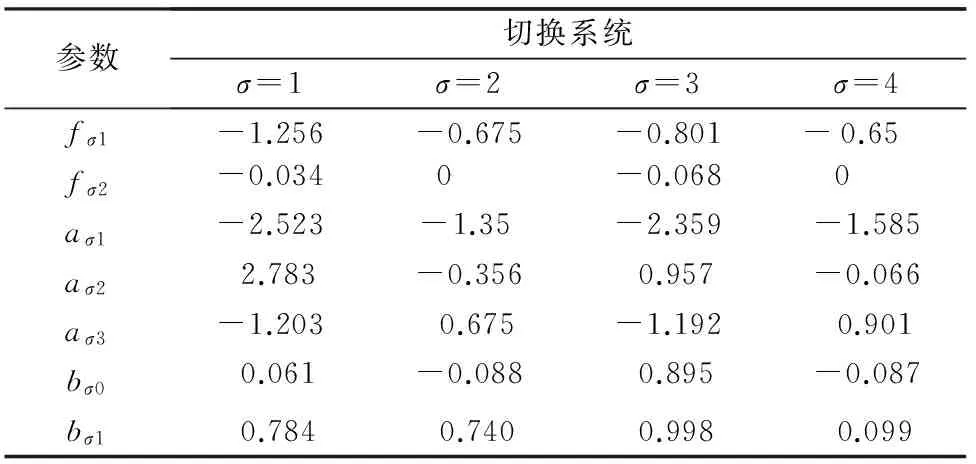
表1 切换系统模型参数辨识结果
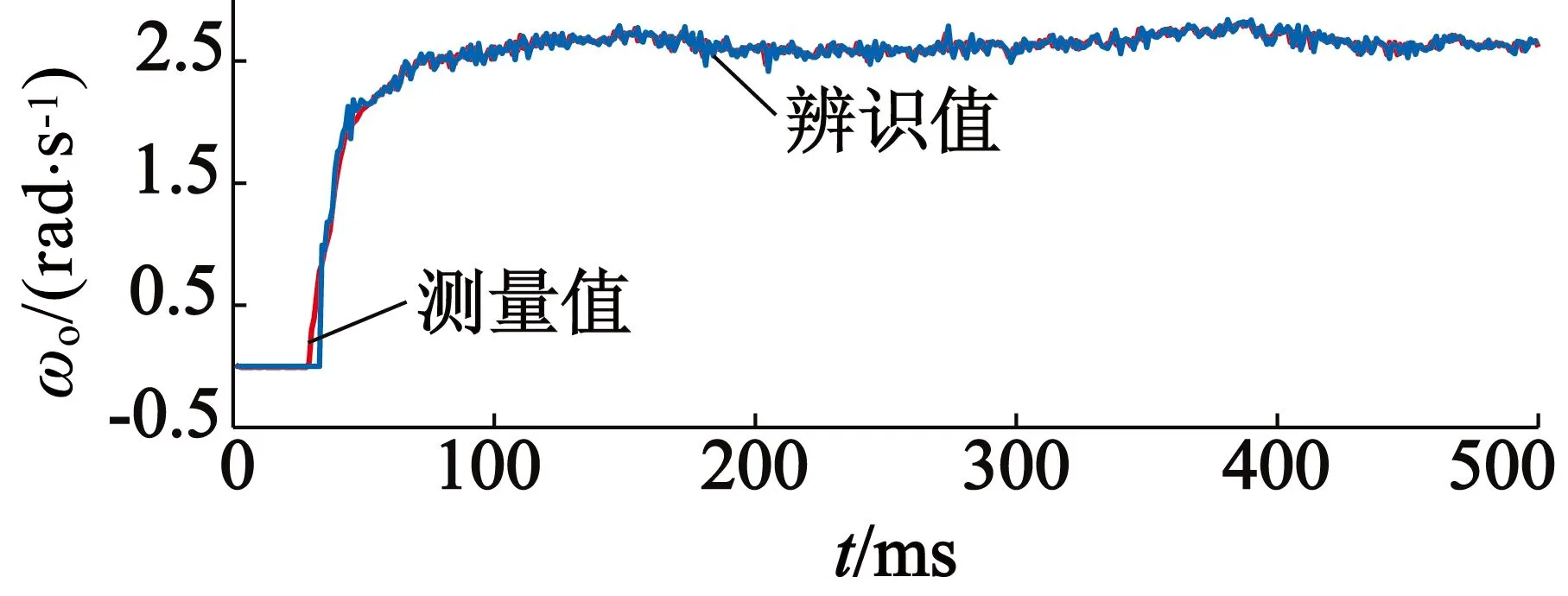
图4 正阶跃信号作用下切换模型拟合结果与现场数对比图
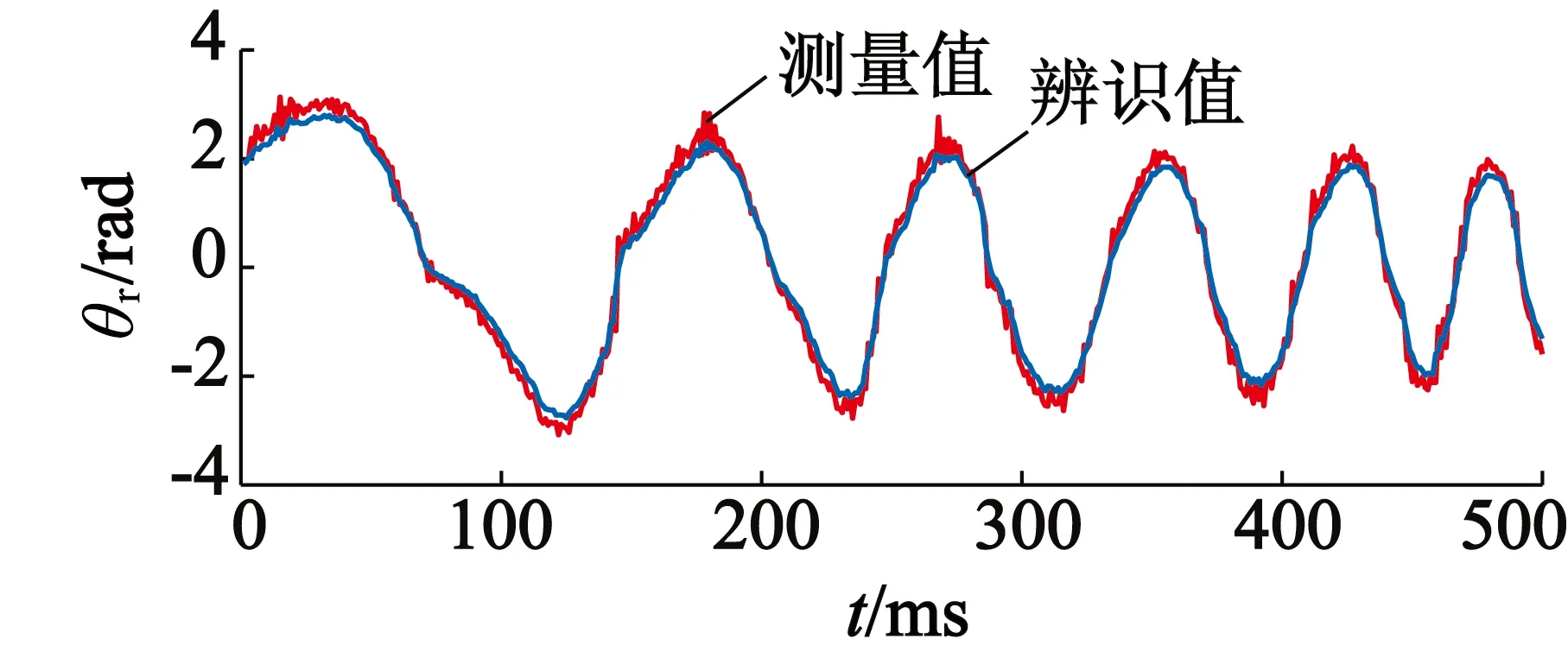
图5 正弦信号作用下角度信息的切换模型拟合结果与现场数对比图
为验证模型的准确性,定义拟合度指标QF[12]:
(11)
式中:N为用于做交叉验证的实验数据中总采样数;y(n)为测量值;yident(n)为辨识值。将图3中记录的实验数据与辨识模型输出数据代入式(11)中,计算所得角速度跟踪的拟合度达99.5%,角位置跟踪的拟合度也在95%以上。可见根据本方法所得切换系统模型能较好地描述系统的输入输出关系。
5 结 语
为描述电机驱动伺服转台的多种运动工况,本文将切换系统理论引入其建模过程,提出了基于切换系统理论的机电伺服转台多工况模型。设计系统辨识实验,获取包括正/负阶跃信号、正弦信号等多组电机驱动转台的现场实验数据。实验结果验证了切换系统建模的必要性。
为进一步准确确定模型参数,本文提出了CMOP,并将多工况下子模型的准确性和平滑切换的条件统一归纳为单目标适应度函数,方便求解。最后,应用MOPSO进行参数辨识,获得了基于切换系统的非线性数学模型及相关参数。
交叉验证结果表明,所建立的非线性切换系统模型具备在多工况下拟合电机驱动伺服转台输入输出关系的能力。所提出的切换系统理论应用、CMOP处理及MOPSO的求解方法是合理、有效的。本文的方法及理论体系还可推广至其他电机驱动伺服系统,用以描述复杂工况下系统特性,为精确控制建立理论基础和被控对象的数学模型。
[1] 郑颖,马大为,姚建勇,等.转台伺服系统负载转矩估计研究[J].微特电机,2014,42(7):40-42.
[2] 李飞,胡剑波,郑磊,等.飞行模拟转台的反推滑模控制优化设计[J].微特电机,2015,43(4):70-74.
[3] 程慧慧.转台的多模式切换控制及其DSP 实现[D].哈尔滨:哈尔滨工业大学,2010.
[4] YOU Wenhu,YAN Ming,WANG Mao,et al.State feedback control of saturated switched systems and its application to turntable[C]//International Conference on Electronic & Mechanical Engineering and Information Technology.IEEE,2011:1017-1020.
[5] 游文虎,颜明,赵建妮.饱和切换系统的滑模控制及其在转台中的应用[J].哈尔滨理工大学学报,2012,17(6):21-24.
[6] ZHANG Qian,WANG Qunjing,LI Guoli,et al.Identification of switched Hammerstein model for radar antenna servo system using the RLS-PSO algorithm[J].Journal of Computational Information Systems,2014,10(3):1077-1084.
[7] 叶超,李才阳.基于PSO的Hammerstein模型辨识及其在雷达伺服系统应用[J].电气传动,2013,43(5):59-62.
[8] ZHANG Qian,WANG Qunjing,LI Guoli.Switched system parameters identification based on the multi-objective particle swarm optimization[J].International Journal of Control,Automation and Systems,2016,14(5):1153-1159.
[9] 陈金辉, 陈辰, 董飚.基于自适应策略的改进粒子群算法[J].计算机仿真,2015,32(3):298-303.
[10] 唐和生,许锐,薛松涛,等.基于CLPSO算法的结构系统识别[J].振动、测试与诊断,2010,30(6):605-611.
[11] 金鹏,李晶.基于改进粒子群算法的BLDCM分数阶速度控制器的研究[J].微特电机,2016,44(7):59-62.
[12] KUKREJA S L,KEARNEY R E,GALIANA H L.A least-squares parameter estimation algorithm for switched hammerstein systems with applications to the VOR[J].IEEE Transactions on Biomedical Engineer,2005,52(3):431-444.

